风力发电系统可靠性评估体系
,,,健美,,,江林(.国网四川省电力公司技能培训中心,四川 成都 633;.成都信息工程大学控制工程学院,四川 成都 605)
0 引 言
中国“十二五”规划以来,风力发电技术迅猛发展,装机容量大幅增加,已成为可再生能源中技术最成熟、应用最广泛的发电技术之一。由于风电具有间歇性、波动性和随机性等特点,使得大规模风电接入电力系统后带来了不确定的因素,因此如何准确评估风力发电系统的可靠性显得非常重要[1-2]。
国内外相关学者对风力发电系统的可靠性评估进行了大量的研究工作。文献[3]从风电接入电网后对系统备用容量的需求入手,分析了风电并网后的系统可靠性问题。文献[4]建立了计及尾流效应的风电场可靠性模型,为研究风电场对电力系统可靠性的影响以及确定风电场可信度打下基础。文献[5-6]用超拉丁概率抽样方法模拟实际风速分布,以及风力发电机的输出功率概率分布,得到基于超拉丁采样的风力发电系统蒙特卡罗可靠性评估法。
以上文献均未考虑风力发电系统的结构特点及元件状态。下面首先分析了风速与风电机组输出功率的关系、风力发电系统的结构特点;其次提出了期望故障受阻电能相等的方法,根据风资源情况和风力发电系统元件状态对风力发电系统可靠性状态进行划分,并建立相应的可靠性指标体系;最后结合实际风电场历史运行数据,对可靠性评估指标体系进行统计,从而完成对风力发电系统进行可靠性评估。
1 风力发电系统的特点
由于风速具有随机性、波动性和间歇性等特点会导致风电机组输出功率的波动性变大,同时风力发电系统的结构特点和元件的可靠性也决定了风力发电系统的输出功率。
1.1 风机输出功率影响因素分析
风机由于其能量转换原理限制,其输出功率主要受季节气候和风速的影响。
1)季节与时间的影响
中国“三北”地区风资源较为丰富。一般来说,一年中春季和冬季风资源较丰富,夏季风资源较贫乏;在一天中来说,白天风资源较贫乏,而夜晚风资源较丰富[7]。
2)风速大小的影响
风电机组的运行状态和输出功率都与风速息息相关。图1给出了风电机组输出功率与风速的曲线[8]。

图1 风电机组输出功率曲线
从图中可以看出,曲线分为4段:当风速小于切入风速时,风机输出功率几乎为0;当风速处于切入风速和额定风速区域内时,风机输出功率与风速近似为线性关系;当风速位于额定风速和切除风速区域内时,风机输出功率为额定功率;当风速大于切除风速时,风机输出功率为0。因此,将风力发电系统状态按照风资源的充裕度进行划分:资源停运、资源限制减额运行和全额运行状态。
1.2 系统结构特点分析
实际风电场中采用辐射状的连接方式,通过电缆将风力发电机组依次连接起来,并汇集到变压器,如图2所示。图中n台风电机组连接成1“串”,同时m串机组并联汇入1台变压器,多台变压器并联接入母线。在同一可靠性标准下,用1台相同容量的发电机组等效替代风电机组“串”。
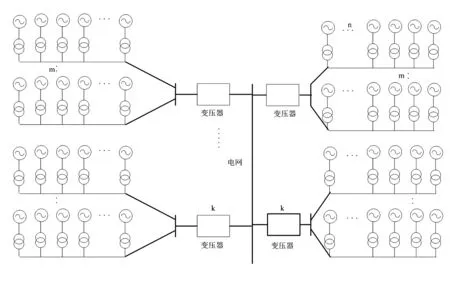
图2 风力发电系统基本构架
根据这些结构特点,可知单台风电机组故障时,会导致所在风电机组“串”输出功率降低,可以认为机组“串”处于部分停运状态;如果变压器出现故障,将会导致与变压器相连的所有风电机组停运。因此按照元件状态对风力发电系统运行状态可划分为:故障停运、故障减额运行和全额运行状态。下面针对风力发电系统结构进行详细分析。

1—风力发电机;2—接触器;3—塔筒内电缆;4—风机出口箱式变压器;5—中压断路器;6—隔离开关图3 单台风力发电机组结构
风力发电机组的结构如图3所示,当风力发电机、接触器、箱式变压器、中压断路器中任何一个元件故障时,这个风电机组将停运。由于中压断路器具有隔离作用,单台风电机组故障停运后,不会影响到同一电缆连接的其他机组正常运行。因此单台风电机组的综合故障停运率为
(1)
与此同时,隔离开关的故障也会引起风电机组的停运。当隔离开关的数量大于1时,隔离开关故障时会导致风电机组停运范围扩大。隔离开关对可靠性的影响主要有2种情况:
1)当风机位于“串”的末端时,即中压断路器通过隔离开关直接与电缆相连,此时中压断路器、隔离开关、电缆L的故障将造成末端风电机组的停运,如图4所示。其停运率为
(2)
式中:Q1为末端风机的故障停运率;qL为电缆L的故障率;q1~q6为图4中元件1~6的故障停运率。

图4 末端风电机组结构
2)当风电机组位于“串”的中部时,2台隔离开关分别连接前后2台风机,其连接如图5所示。导致风机停运的主要原因有:中压断路器B、隔离开关S1、S2或电缆L故障。根据期望故障受阻电能不变的原则[9],对系统运行状态进行划分,将系统运行状态出现的概率乘以该状态下系统的输出功率,并进行累加,再除以机组装机容量得到等效故障停运率,即
(3)
式中:Qn为n台风电机组经串联连接后的等效故障停运率,采用层次迭代法得到;Qn-1为n-1台风电机组经串联连接后的等效故障停运率;Q1可以由式(2)计算得到。

图5 中部风电机组结构
根据电力系统串并联方式后的可靠性计算公式[10],“m串”风电机组并联后的停运率Qp为
(4)
并联后的风电机组“串”再与变压器串联后,得到风电-变压器组的停运率QPI为
QPI=QP+Q1
(5)
根据上述分析,将风力发电系统故障分为系统完全故障和系统部分故障两类:
1)K组风机-变压器组并联发电系统完全故障概率QC为
(6)
2)在实际过程中,由于风力发电系统中风机-变压器组较多,所以发生完全故障的概率并不大,更多时候是由于风电机组或变压器引起的系统部分故障。
当风力发电机组串发生故障,由于风力发电机组“串”间相互独立,且系统停运概率服从二项分布,风电机组“串”停运率Q1P可按式(7)计算。
(7)
当变压器故障,采用类似的分析方法,得到部分变压器停运率Q2P为
(8)
由于风力发电机组“串”和变压器的故障相对独立,所以得到系统部分停运率QP为
QP=Q1P+Q2P
(9)
综上,风力发电系统的可靠性取决于风资源和风力发电系统的结构。通过计及风资源和系统架构的特点,建立多状态风力发电系统可靠性模型。
2 可靠性状态的划分
可以根据风资源和元件状态将风力发电系统的可靠性状态划分为以下几种情况:
1)全额运行状态:当风速较快时,即风力发电系统输出功率能够达到总装机容量的70%以上。
2)资源限制减额运行状态:当风速较慢时,即风力发电系统输出功率低于总装机容量的70%。
3)故障减额运行状态:风力发电系统部分元件故障导致输出功率减少的状态。
4)故障停运状态:风力发电系统全部停运的状态。
5)无风或风速过快停运状态:当风速处于无风或者风速过快状态时,风力发电系统由于风资源停运的状态。
3 可靠性指标体系
针对第2节中的可靠性状态,下面从时间、出力、系统等方面建立风力发电系统可靠性指标体系,该体系可以反映出风力发电系统各状态的特性。
3.1 时间指标
将风力发电系统时间指标体系按照图6所示方式进行划分。

图6 时间指标体系
结合系统状态,状态时间指标如下:
1)全额运行时间FRH(full run hour):风力发电系统处于全额运行状态(即输出功率达到总装机容量70%)的累计运行时间。
2)资源限制减额运行时间RDH(resource deduction hour):风力发电系统由于风速的限制,输出功率小于总装机容量的70%的累积运行时间。
3)故障减额运行时间FDH(fault deduction hour):风力发电系统中部分元件故障,导致输出功率减小的累积运行时间。
4)故障停运时间FOH(fault outage hour):风力系统由于元件故障发生全站停运的累计时间。由FOH=PH·QC计算。
5)无风或风速过快停运时间NH(not use hour):系统处于无风或风速过快状态下的累计时间。
6)年利用小时数UH(utilization hours):风力发电系统的年发电量除以系统总装机容量折算的发电小时数。
7)减额运行时间DH(deduction hour):风力发电系统由于元件故障或者风资源限制,输出功率小于70%额定功率的运行时间,DH=FDH+RDH。
8)运行时间RH(run hour):风力发电系统处于运行状态的累计时间,RH=FRH+DH。
9)停运时间OH(outage hour):风力发电系统处于完全停运的累计时间,OH=FOH+NH。
10)周期时间PH(period hour):年统计时间8 760 h。
3.2 出力状态指标
1)全额等效出力FEP(full equivalent power):风力发电系统在全额运行状态下的等效输出功率。
2)资源限制下减额等效出力RDEP(resource deduction equivalent power):风力发电系统由于风速降低导致减额运行状态下的等效输出功率。
3)故障减额等效出力FDEP(fault deduction equivalent power):风力发电系统由于部分元件故障导致系统减额运行的等效输出功率。
4)减额等效出力EDP(equivalent deduction power):风力发电系统由于风速降低或者部分元件故障导致系统减额运行的等效输出功率。
5)等效出力EP(equivalent power):风力发电系统在年统计时间内等效恒定输出功率。
6)等效出力系数ECF(equivalent coefficient factor):风力发电系统等效输出功率与额定输出功率RP(rated power)的比值,ECF=EP/RP。
7)最大出力MP(maximum power):风力发电系统实际发电中的最大输出功率。
8)最大出力系数MPF(maximum power factor):风力发电系统实际发电中最大输出功率与额定功率的比值,MPF=MP/RP。
3.3 系统总体指标
为反映风力发电系统总体情况,其系统指标如下:
1)设计可用率DU(design usability):根据风力发电系统停运概率和修复时间得到系统可用率设计值,DU=1-QC。
2)运行系数OF(operating factor):风力发电系统实际运行状态的概率,OF=RH/PH。
3)年发电设备利用率EUR(the annual power generation equipment utilization rate):风力发电系统发电设备利用的概率,EUR=UH/PH。
4)全额运行率FRR (full run rate):风力发电系统处于全额运行状态的概率,FRR=FRH/PH。
5)资源限制减额运行率RDR(resource deduction rate of operation):风力发电系统实际中由于风速限制导致系统处于减额运行状态的概率, RDR=RDH/PH。
6)设备故障减额运行率EFDR(equipment fault deduction rate of operation):风力发电系统由于部分元件故障,导致系统处于减额运行状态的概率, EFDR=FDH/PH。
7)暴露率EXR(exposure rate):风力发电系统利用风能的效率,等于年利用小时数与系统运行时间的比值,EXR=UH/RH。
4 算 例
采用实际风电场作为算例,验证所提出的可靠性模型与指标体系的准确性与可行性。实际风力发电系统总装机容量为30 MW,相邻风电机组间的距离为500 m,5台风电机组组成1“串”,3组风力发电机组串并联接入变压器。
采用文献[12-14]的统计数据作为实际算例的系统元件参数,如表1所示。实际输出功率曲线为张家口某风电场实测数据(2015年9月1日至2016年8月31日),如图7所示。

表1 风力发电系统各元件可靠性参数

图7 8 760 h输出功率曲线
4.1 系统故障分析
分析系统故障情况,n=5,m=1,k=3,根据式(1)得:
qWTG=0.086 3
当负荷开关数为1时,其等效故障概率为
Q1=0.087 1
由5台风力发电机组成的“串”的等效故障概率为
Q5=0.089 8
风电-逆变器组的故障概率为
QPI=QP+Q1=0.171 3
若统计时间PH取8 760 h, 由式可得故障停运时间为
FOH=PH·QC≈44 h
当系统部分元件故障时,由于同一变压器有3“串”风电机组接入,故将系统的部分元件故障分为单 “串”风电机组故障和两“串”风电机组故障,其停运概率计算过程分别为
则可得系统部分故障参数如下:
QP=QP1+QP2=0.425 9
由FDH=PH·QP得到由于部分元件故障导致系统减额运行的时间大约是3 731 h。
根据以上分析还可以计算风力发电系统由于故障减额下的输出功率与系统正常状态下输出功率的比值KP:
4.2 指标统计与计算
将图7中的实际风电场输出功率数据按照第3节中的指标体系进行统计,对该风力发电系统可靠性进行评估,结果如图8至图10所示。

图8 时间指标结果
从图8可以看出,风力发电系统由于元件故障导致系统全站停运时间最少;风力发电系统停运时间约为1 200 h,占全年的13.7%;运行时间远超过停运时间,说明风电场所处环境和运行状态较好;系统全额运行时间只占整个运行时间的13%,由于风速降低导致系统减额运行时间占运行时间的比例达87%,说明本地的风速波动性较大;年利用小时数仅为1 882 h,反映了风力发电系统资源利用效率偏低。
从图9可以看出:风力发电系统全额等效输出功率约占总装机容量的68.8%,由于风速降低导致系统减额等效输出功率占11%;由于元件故障导致系统减额等效输出功率占41.9%,说明风资源的充裕度对风力发电系统的输出功率影响较大。风力发电系统等效输出功率仅占总装机容量的21.5%,系统统计时间内最大输出功率为24.485 MW,占总装机容量的81.6%。

图9 出力状态指标结果
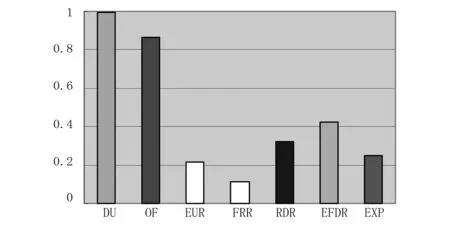
图10 系统总体指标结果
从图10可以看出:风力发电系统可用率设计值达到99.5%,运行系数达到86.3%,说明风力发电系统的可用率较高;元件故障减额运行率达到42.59%,这反映了风力发电机组的停运概率偏高,符合风电场实际运行情况。因此,通过提高元件的可靠性是实现降低风电场故障减额运行概率的主要方式之一。年发电设备利用率为21.48%,暴露率为24.89%,反映了风能资源的限制造成系统利用能源的效率降低,如果采用变转速风力机组或采用主动式风流动智能控制系统,则可以有效提高风电场暴露率,进一步提高系统可靠性[15]。
5 结 语
随着风电技术的快速提升,发电成本大幅降低,风力发电的技术优势和经济性将不断显现出来,作为重要的新能源之一,装机容量将不断提高。前面从风力发电系统结构入手,深入研究了基于元件故障和风资源充裕度对风力发电系统可靠性的影响。根据风力发电系统结构特点,按照期望故障受阻电能相等的方法,用相同容量的发电机来等效替代风电机组“串”,并建立了考虑元件状态和资源约束的系统状态。从时间、出力、系统3个方面建立风力发电系统可靠性评估指标体系,并对其进行可靠性评估。算例分析表明,基于元件状态和风资源限制的可靠性模型,可以真实反映实际系统的可靠性。
[1] Rajesh Karki, Po Hu, Roy Billinton, A Simplified Wind Power Generation Model for Reliability Evaluation[J]. IEEE Transactions on Energy Conversion,2006,21,(2): 533-540.
[2] Francois Vallee, Jacques Lobry, Olivier Deblecker.System Reliability Assessment Method for Wind Power Integration[J]. IEEE Transactions on Power System,2008,23 (3):1288-1297.
[3] Ronan Doherty, Mark O Malley. A New Approach to Quantify Reserve Demand in Systems With Significant Installed Wind Carpacity[J].IEEE Transactions on Power Systems,2005,20(2):587-595.
[4] 张硕,李庚银,周明,等.风电场可靠性建模[J].电网技术,2009,33(13):37-41.
[5] 吴义纯,丁明.基于蒙特卡罗仿真的风力发电系统可靠性评价[J].电力自动化设备,2004,24(12):70-73.
[6] 刘威,赵渊,周家启,等.计及风电场的发输配电系统的可靠性评估[J].电网技术,2008,32 (13):69-74.
[7] 温敏,张人禾,杨振斌.气候资源的合理开发利用[J].地球科学进展,2004,19(6):896-901.
[8] 梁惠施,程林,刘思革.基于蒙特卡罗模拟的含微网配电网可靠性评估[J].电网技术,2011,35 (10):76-81.
[9] 李文沅.电力系统风险评估模型、方法和应用[M]. 北京:科学出版社,2006.
[10] 郭永基. 电力系统可靠性分析[M]. 北京:清华大学出版社,2003.
[11] 王震,鲁宗相,段晓波,等.分布式光伏发电系统的可靠性模型及指标体系[J].电力系统自动化,2011,35(15):18-24.
[12] Johan R, Lina M B.Survey of Failures in Wind Power Systems with Focus on Swedish Wind Power Plants During 1997-2005[J].IEEE Transactions on Enerey Conversion,2007,22(1): 167-173.
[13] Rajesh Karki, Po Hu. Wind Power Simulation Model for Reliability Evaluation[C]. IEEE CCECE/CCGEI, Saakatoon, 2005.
[14] Ubeda J R, Rodriguez G M. Reliability and Production Assessment of Wind Energy Production Connected to the Electric Network Supply[J].IEEE Proceedings on Generation Transmission and Distribution,1999,146(2):17-19.
[15] 沙非, 马成廉,刘闯. 变速恒频风力发电系统及其控制技术研究[J].电网与清洁能源,2009,25(1):44-47.

