民用无人机姿态稳定与航迹跟踪控制策略研究

冯军红, 俆开俊, 林娜

(中国民航飞行学院 飞行技术学院, 四川 广汉 618307)

近年来，国内外民用无人机产业蓬勃发展，给各行业带来了巨大的效率提升，其最大的特点和活力就是功能载荷的多样化[1-3]，市场研发的关注点也在于此。然而，民用无人机功能载荷多变，例如不同功能载荷的替换/挂载，货运无人机货箱装卸/投放等，其内外部参数的变化和复杂的应用环境给民用无人机操纵性能和航迹跟踪能力带来了不小的挑战[4]。

针对无人机飞行稳定控制和航迹跟踪问题，众多学者从不同角度开展了富有成果的研究。王大伟等人[5]针对四旋翼欠驱动、强耦合非线性系统航迹跟踪问题，提出了一种滑模航迹跟踪控制策略，其姿态和位置控制具有良好的效果。陈鹏等人[6]结合PID控制法与智能模糊控制算法,设计了一种自适应模糊PID无人机姿态控制器，提高了无人机抗干扰性能。杨雨婷等人[7]为解决民用无人机飞控系统的高可靠性、实时性等要求，将AADL语言应用于民用无人机飞控系统建模与分析中，减小了后期系统发生错误的概率。吕海龙[8]根据单向辅助面滑模控制方法，设计了系统内外回路的姿态控制器，保证了无人机机动飞行过程的安全性与稳定性。杨恩泉等人[9]对无人机机动飞行航迹跟踪系统的内环采用非线性动态逆方法，外环采用逆动力学前馈加模糊反馈的控制结构，提高了飞行航迹的跟踪精度。上述研究提出的控制方法都取得了较好的控制效果，但是针对载机自身参数变化和外部干扰所带来的被控模型变化问题考虑不足，当载荷多变或外界干不确定性因素叠加时仍将导致跟踪误差增大。

本文针对民用无人机功能载荷多变的特点，充分考虑外部扰动及参数不确定性情况，将区间系统控制理论引入内环稳定控制器设计中，保证模型区间变化过程中无人机姿态的稳定控制。此外，为解决民用无人机航迹跟踪精度问题，以航向控制为例给出了一种航迹跟踪控制方法。仿真结果表明所设计的内外环控制系统能够控制无人机跟踪期望的航迹，取得了较好的控制效果。

1 无人机系统建模

1.1 非线性模型与仿真模块搭建

要完成姿态的稳定控制和航迹跟踪控制，首要问题就是建立无人机运动的数学模型[10]，任意刚体飞行器空间运动的6个自由度为：3个质心运动和3个角运动。6个自由度的无人机运动分成2组：只包含对称面内的纵向运动及非对称面内的横侧向运动。纵向运动包含1个角度运动和2个线运动，而侧向运动有2个角运动和1个线运动。对于各向线运动和角运动，根据经典牛顿物理学定理可以得到无人机刚体运动的12个非线性微分方程，限于篇幅限制，这里不再具体给出，相关坐标系和参数变量定义具体可见文献[10]，下面列出某型民用无人机主要系统参数[10-11]，如表1所示。

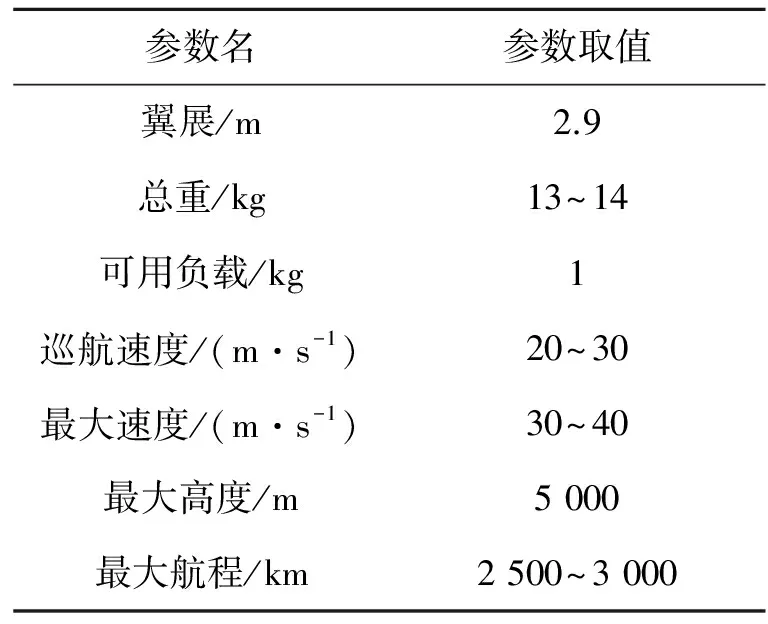
表1 某型民用无人机主要参数

为了保证后续姿态稳定和航迹跟踪控制方法的研究和仿真分析，对上述六自由度运动数学方程，按照图1所示进行模块搭建，以仿真某型民用无人机实际飞行状态。

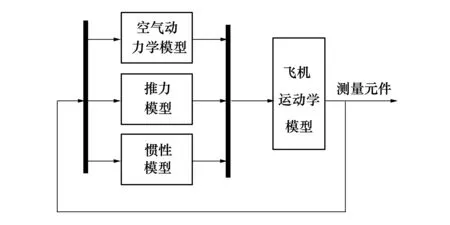
图1 无人机飞行仿真模块

所搭建的六自由度非线性模型方程，可以表示为如下通用的非线性状态方程：

=f(x,u)

y=g(x,u)

(1)

式中,x为系统状态变量,u为系统输入,y为系统量测输出,f为非线性状态方程函数,g为非线性输出方程。

1.2 纵向线性化处理

由于无人机的六自由度运动方程中所有运动参数都是非线性函数,对于理论分析和一体化控制而言较为复杂,需要借助参数小扰动方法[12-14]进行线性化处理和纵横侧向解耦。在设定无人机初始飞行速度和飞行高度的情况下,最终可将非线性飞行控制方程式转化成标准的线性状态方程[A,B,C,D]的形式[15]。以横侧向运动过程为例,在(1)式中,其状态向量为:x=[v,p,r,φ,ψ]′,观测输出量为:y=[β,p,r,φ,ψ]′,控制量为:u=[δa,δr]′,其中v表示速度矢量在机体坐标y轴上的分量,p和r分别表示飞机绕机体x轴和z轴的转动角速度,φ和ψ分别表示滚转角和偏航角,β表示侧滑角,δa表示副翼舵偏角,δr表示方向舵偏角。根据上述线性化方法,可以方便得到对应的状态空间表达式。

2 基于区间系统理论的无人机姿态稳定控制

2.1 区间系统理论及无人机区间模型

民用无人机功能载荷的变化,以及本身被控对象模型参数的变化和外部扰动等,从理论上讲可以归纳为系统模型本身在一定范围内的变化,因此可看作区间系统,从而可以利用区间系统鲁棒控制方法完成对无人机的稳定控制建模。按照上一小节线性状态方程表达形式,假定以下被控系统描述:

=Ax(t)+Bu(t)

(2)

式中,x∈Rn为n维状态向量,A∈Rn×n为系统矩阵,B∈Rn×p为控制矩阵,u∈Rp为p维控制输入。而矩阵A和B描述为下述区间形式:

A∈N[P,Q],B∈N[S,T]

(3)

式中,P,Q和S,T分别为系统矩阵和控制矩阵的上界和下界。

根据某小型无人机飞行的主要特征工作点,选择其两个边界点作为上述区间模型(3)式的边界,以验证本节所提区间系统控制器设计方法,即特征点1:飞行速度为30 m/s,飞行高度为500 m;特征点2:飞行速度为23 m/s,飞行高度为200 m。

A1=

-0.798 90.643 4-29.992 79.785 10

-5.274 2-25.974 112.501 100

0.856 0-3.369 1-1.306 600

010.021 500

001.000 300

B1=-2.054 65.244 3

-180.394 23.245 8

-7.112 7-33.135 7

00

00

A2=

-0.637 31.513 6-22.949 99.796 50

-4.191 5-20.626 69.927 400

0.679 8-2.675 5-1.037 600

010.066 000

001.002 200

B2=-1.250 93.192 8

-109.988 41.976 1

-4.330 4-20.173 8

00

00

上述2个系统的系统矩阵和控制矩阵就等同于(3)式中系统矩阵和控制矩阵的上下界。由于系统可观,以下2.2小节的状态反馈控制可以通过构建状态观测器来实现,这里对于观测矩阵C和控制矩阵D由于篇幅有限不再赘述。

2.2 姿态稳定控制器设计

基于区间系统理论的无人机姿态稳定控制器的主要任务,是保证在外部扰动、负载变化和参数不确定性情况下整个系统的飞行稳定,基于经典的区间系统鲁棒控制理论可得到如下定理[13,16]:

定理带状态反馈控制器的系统式(2)是稳定的,若存在正定矩阵X和实常数ε>0满足以下Riccati方程:

FTF+εI=0

(4)

式中

A0=P+Q2,B0=S+T2,

G=T-S2,H=Q-P2,

E=[h11e1…h1ne1…hn1en…hnnen]

F=[h11e1…h1nen…hn1e1…hnnen]T

EB=[g11e1…g1pe1…gn1en…gnpen]

FB=[g11f1…g1pfp…gn1f1…gnpfp]T

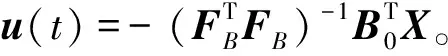
对于被控系统式(2),为保证方程式(4)的求解,将实常数ε设置为0.3,可以得到区间系统鲁棒控制器为:

K=0.022 70.112 7-0.082 2-0.272 6

0.006 70.090 8-0.186-0.118 7

3 横侧向航向航迹跟踪控制

3.1 航迹跟踪运动学模型

民用无人机实际飞行过程中,在上述内环稳定性修正基础上,要求其外环具备较好的航迹或航迹跟踪能力,解决传感器存在较大误差情况下的跟踪效果差及收敛速度慢甚至发散等问题。假设已知无人机相对于目标航迹线的横向、纵向距离和速度分别为(X,)、(Y,),如图2所示。

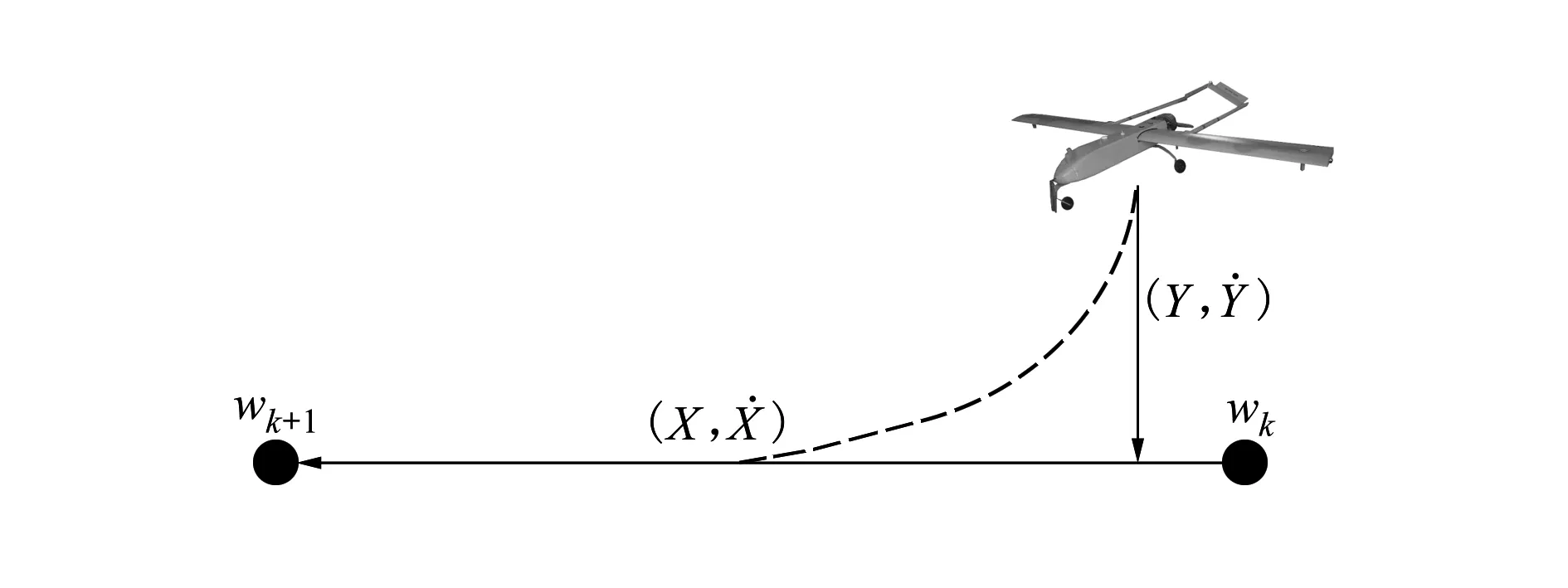
图2 航迹跟踪示意图

针对无人机外环航迹控制问题,根据图2航迹跟踪原理,基于图3所示的坐标系可建立风场条件下飞行器质点平面航迹运动方程(5):

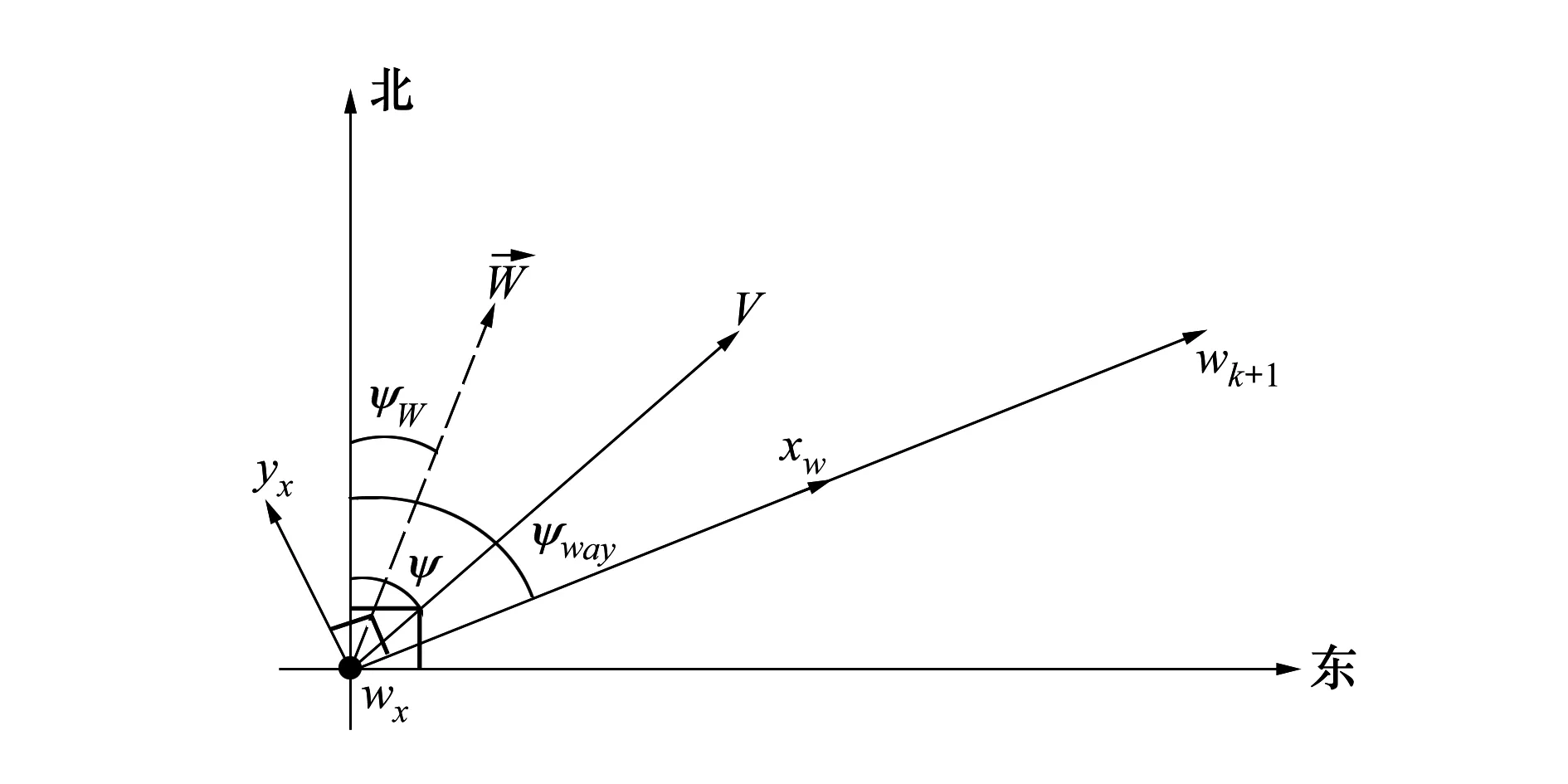
图3 无人机平面质点运动示意图

uc=

(5)

式中,V为空速矢量,W为外部风速,偏航角ψ为速度矢量V和地理北向的夹角,而风向角ψW为风速W和地理北向的夹角,航路偏角ψway是预定航路航向和地理北向的夹角,uc即为期望的航迹跟踪指令。

3.2 航迹跟踪控制方法

由图2所示,航迹跟踪控制需要设计外环控制率,以倾斜转弯BTT(bank to turn)方式控制飞机跟踪相邻航路点间的航迹。假设xy轴两向的速度与xy轴两向位移方向一致,如图4所示的速度矢量VOB和VOA,位置矢量SOB′和SOA′。

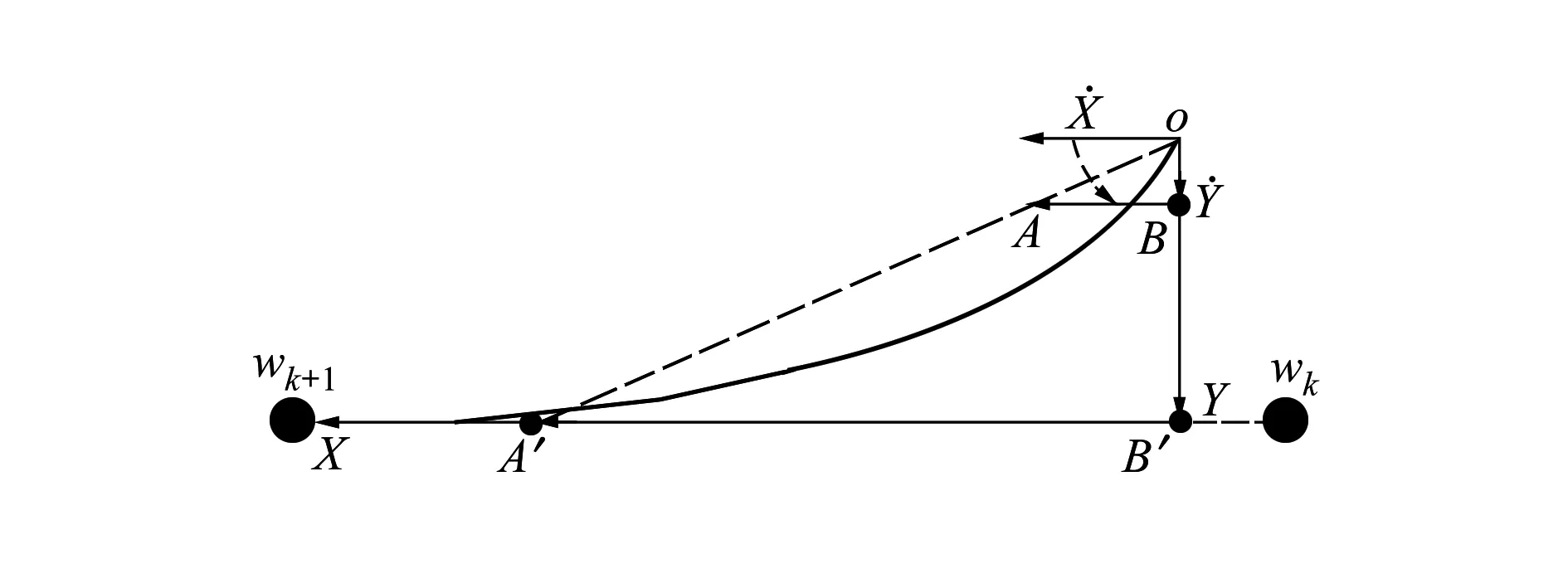
图4 横侧向航迹控制方法

根据图4所示,可以得到矢量表达:

VOBSOB′=VOASOA′⟹kX=Y

(6)

根据(5)式,定义实际飞行过程中的航向偏差E为kX·-Y·,而期望的航迹跟踪指令需要基于这一偏差来完成航向的修正,uc(t)=K·E=K(kX·-Y·),这其中k为图3所示xy向的权重因子,K为控制律比例系数。

4 组合控制律仿真与验证

4.1 内环姿态稳定仿真

首先搭建了包含区间鲁棒控制律的横侧向民用无人机系统闭环仿真环境,并采用模型变化来模拟实际工程中功能载荷模块变化所带来的模型不确定性和外界复杂环境干扰问题,为了考核闭环系统姿态稳定效果,在给定偏航角指令的情况下,给出了仿真结果如图5和6所示。

图5中,模型1～3分别表示(3)式中(R0,B0)模型,以及2.1小节特征点1和2模型。图6中,噪声1,2,3表示在闭环系统状态采集处叠加不同幅度的白噪声。可以看出,载荷变化和外界干扰对系统响应虽然造成了一定的短时影响,而本文设计的姿态稳定控制器能够很好地满足控制要求,解决了无人机的姿态稳定问题。

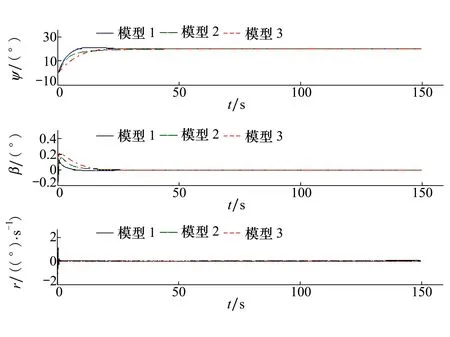
图5 载荷变化情况下系统仿真曲线

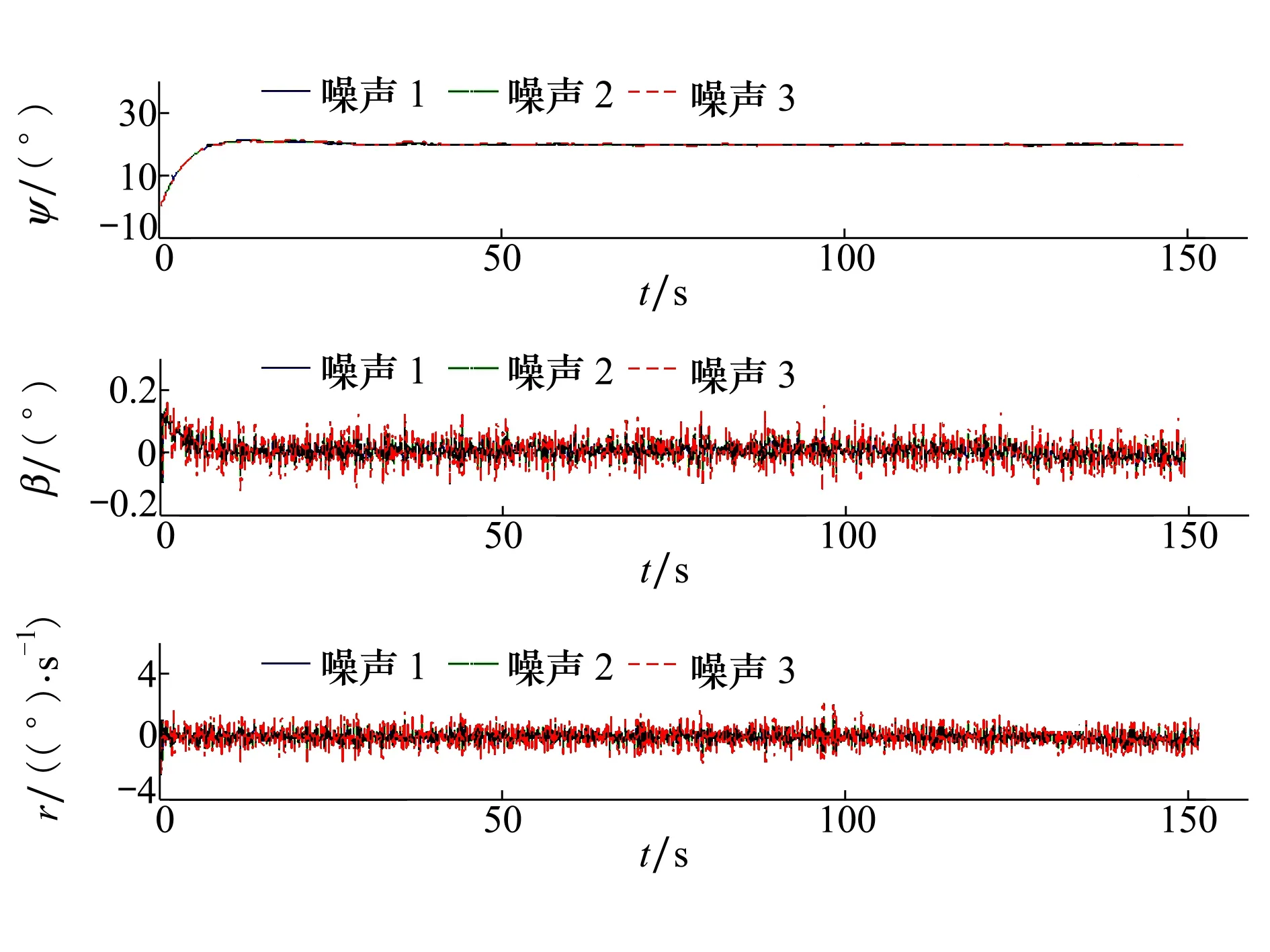
图6 外界干扰情况下系统仿真曲线

4.2 外环航迹跟踪控制仿真

首先设定仿真环境如下:无人机以定速30 m/s飞行,在初始时刻存在北向1 km的航迹偏差,初始航向为北偏东60°;飞行区域存在定常的北向风,风速为5 m/s,飞行器内环受到环境测量噪声干扰影响。

假定无人机对自身航迹点和目标航迹能够精确探测,按照3.2小节所设计的外环航迹跟踪控制方法向目标航迹矢量进行修正,权重因子k为0.4,对x向的误差相对重视,航迹控制系数增益设置为0.000 5,由此得到无人机航迹跟踪效果如图7所示。图7上半部分所示，无人机在初始60°航向且受到北向定速风影响下，通过航迹控制律顺时针偏转并逐步向目标航迹进行贴近，最终回到指定航迹线，该过程中无人机不断修正自身航向角，保证向目标航迹的靠拢。由此航迹跟踪控制很好地实现了外环航迹的控制，达到了航迹修正的控制精度。

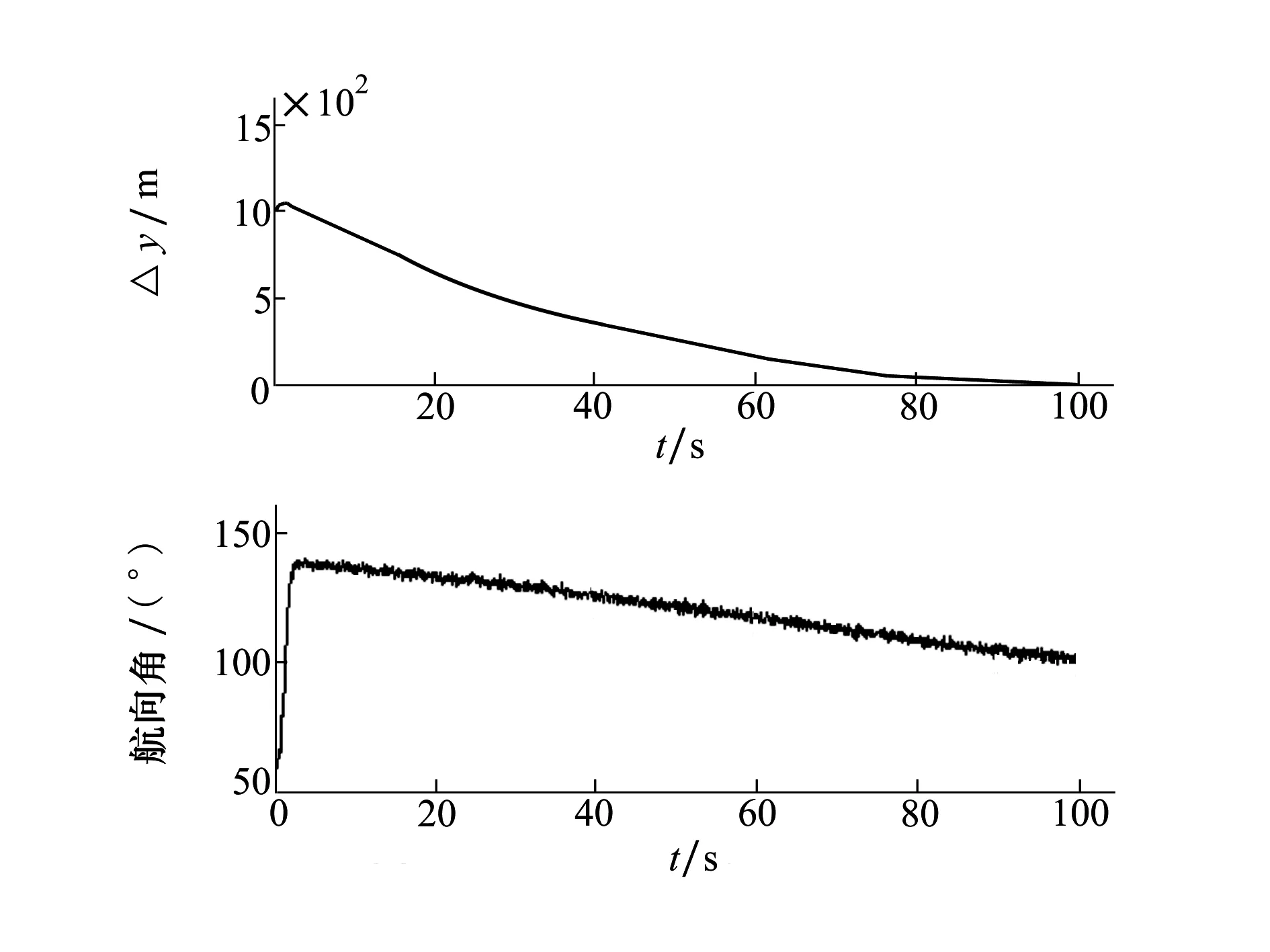
图7 无人机航迹跟踪控制曲线

根据控制律仿真和验证可知,本文所设计的控制器具备载荷变化和复杂环境下的姿态稳定控制和航迹跟踪能力,能有效克服被控模型变化带来的控制效果恶化和航迹误差缺陷问题,在外界噪声等环境因素影响情况下可以保障无人机稳定飞行及航迹跟踪效果,研究结果对民用无人机实际控制律设计有一定的参考价值。

5 结 论

民用无人机广泛应用背景下功能载荷多变，存在被控系统模型区间变化，以及复杂环境影响情况下的航迹跟踪误差。针对这一问题，本文引入区间系统鲁棒控制方法，解决功能载荷变化所带来的被控对象模型不确定性，运用基于动态航向误差的航迹控制方法，抑制了复杂飞行环境所带来的航迹跟踪误差。通过内外环协调配合的控制策略，实现了民用无人机系统的姿态稳定与航迹跟踪控制。

参考文献：

[1] 王柯, 付怡然, 彭向阳,等. 无人机低空遥感技术进展及典型行业应用综述[J]. 测绘通报, 2017(Suppl 1):79-83

Wang Ke, Fu Yiran, Peng Xiangyang, et al. Overview of UAV Low Altitude Remote Sensing Technology and Application in Typical Industries[J]. Bulletin of Surveying and Mapping, 2017(Suppl 1):79-83 (in Chinese)

[2] 陈侠, 乔艳芝. 无人机任务分配综述[J]. 沈阳航空航天大学学报, 2016, 33(6):1-7

Chen Xia, Qiao Yanzhi. Summary of Unmanned Aerial Vehicle Task Allocation[J]. Journal of Shenyang Aerospace University, 2016, 33(6):1-7 (in Chinese)

[3] 杨宝奎. 构建以信息化为主导的无人机应用体系[J]. 飞航导弹, 2015(4):3-8

Yang Baokui. Construction Application System for UAV Based on Information[J]. Aerodynamic Missile Journal, 2015(4):3-8 (in Chinese)

[4] 贺跃帮, 裴海龙, 叶祥,等. 无人直升机的自适应动态面轨迹跟踪控制[J]. 华南理工大学学报:自然科学版, 2013, 41(5):1-8

He Yuebang, Pei Hailong, Ye Xiang, et al. Trajectory Tracking Control of Unmanned Helicopters by Using Adaptive Dynamic Surface Approach[J]. Journal of South China University of Technology:Natural Science Edition, 2013, 41(5): 1-8 (in Chinese)

[5] 王大伟, 高席丰. 四旋翼无人机滑模轨迹跟踪控制器设计[J]. 电光与控制, 2016, (7):55-58

Wang Dawei, Gao Xifeng. Design of Sliding Mode Trajectory Tracking Controllers for Quadrotor Aircraft[J]. Electronics Optics & Control, 2016, (7):55-58 (in Chinese)

[6] 陈鹏, 段凤阳, 张庆杰,等. 基于模糊PID的无人机姿态控制器的设计[J]. 弹箭与制导学报, 2015(1):9-11

Chen Peng, Duan Fengyang, Zhang Qingjie et al. Design of UAV Attitude Controller Based on Fuzzy PID[J]. Journal of Projectiles Rockets Missiles and Guidance, 2015(1):9-11 (in Chinese)

[7] 杨雨婷, 张建伟, 王泊涵,等. 基于AADL的民用无人机飞控软件时间/堆栈分析[J]. 计算机工程与设计, 2017(10):2703-2711

Yang Yuting, Zhang Jianwei, Wang Bohan, et al. Time and Memory Size Analysis of Civilian Unmanned Aerial Vehicle Flight Control Based on AADL[J]. Computer Engineering and Design, 2017(10):2703-2711 (in Chinese)

[8] 吕海龙. 一种基于单向辅助面滑模控制的无人机姿态控制器设计与仿真[J]. 四川兵工学报, 2015(11):112-117

Lü Hailong. Based on Sliding Mode Control with Unidirectional Auxiliary Surfaces of UAV Attitude Controller Design and Simulation[J]. Journal of Sichuan Ordnance，2015(11):112-117 (in Chinese)

[9] 杨恩泉, 高金源. 无人机机动轨迹跟踪系统设计[J]. 飞行力学, 2007, 25(2):30-33

Yang Enquan, Gao Jinyuan. UAV Maneuver Trajectory Tracking System Design[J]. Flight Dynamics, 2007, 25(2): 30-33 (in Chinese)

[10] 吴森堂, 费玉华. 飞行控制系统[M]. 北京:北京航空航天大学出版社, 2005

Wu Sentang, Fei Yuhua. Flight Control System[M]. Beijing, Beihang University Press, 2005 (in Chinese)

[11] Samar R, Shah M Z, Nzar M. Lateral Control Implementation for an Unmanned Aerial Vehicle[J]. ISRN Aerospace Engineering, 2015, 2013(2):24-35

[12] Liu H, Li D, Zuo Z, et al. Robust Three-Loop Trajectory Tracking Control for Quadrotors with Multiple Uncertainties[J]. IEEE Trans on Industrial Electronics, 2016, 63(4):2263-2274

[13] Raffo G V, Ortega M G, Rubio F R. An Integral Predictive/NonlinearH∞Control Structure for a Quadrotor Helicopter[M]. Pergamon Press Inc, 2010

[14] Lu J G, Chen G. Robust Stability and Stabilization of Fractional-Order Interval Systems: an LMI Approach[J]. IEEE Trans on Automatic Control, 2009, 54(6):1294-1299

[15] Liu H, Bai Y, Lu G, et al. Brief Paper-Robust Attitude Control of Uncertain Quadrotors[J]. IET Control Theory & Applications, 2013, 7(11):1583-1589

[16] 史忠科, 吴方向, 王蓓, 等. 鲁棒控制理论[M]. 北京:国防工业出版社, 2003

Shi Zhongke, Wu Fangxiang, Wang Bei, et al. Robust Control Theory[M]. Beijing, National Defense Industry Press, 2003 (in Chinese)