复杂海底结构诱导的非线性内波生成与演进分析

高国兴, 范磊, 王惠刚

(1.西北工业大学 航海学院, 陕西 西安 710072; 2.海军潜艇学院, 山东 青岛 266199)

海洋内波在生成、传播和演进过程中表现出的复杂水下动力学结构以及独特的遥感表面图像特征，是由包括水体水平不均匀的密度分层、海底地形拓扑结构、潮汐变化等多种因素作用的结果。而作为底边界的海底地形，对内波生成和演进过程有不可忽视的影响。例如，在南海北部人们观测到的复杂内波现象[1-4]，被认为是受了台湾岛与吕宋岛之间的恒春海脊和兰屿海脊地形拓扑结构的强烈影响或作用；同样在印度洋安达曼海以及美国西海岸的非线性内波，也被认为可能受到类似复杂海底地形结构变化的影响。通过观测和数值模拟研究可以看出，增加一个海脊后的内波波形明显比单一海脊结构引起的内波波形复杂，主要表现在内孤立波传播时间、波列数量、波列强度等特性的变化。

目前对于内波结构的复杂性，特别是对双海脊影响下的内波特性研究在进一步深入。Vlasenko等[5]在南海北部海洋内波研究中，应用MITgcm海洋模型，对双海脊的海底结构进行了研究，模拟了当海脊深度不同时产生的不同形式的孤立波，认为第2个海脊可能主要影响内波第2模态，并且强度较弱；而Alford等[1]利用了Ramp[3]的实验数据，对南海内波中2种不同形式孤立波(A波和B波)进行了分析，认为可能是全日或半日潮的作用产生了2种不同形式的波形。但是通过模拟分析，我们认为第2个海脊的作用可能并不弱；Guo等结合Alford的数据[2]，并应用MITgcm模型对南海内波进行了研究，进一步说明了海脊对内波生成和传播演化过程有较大影响。

尽管一些海洋动力学模型能够较好地模拟内波的传播演化过程，但对于复杂海底地形影响等因素激发的内波及其演进，特别是双海脊影响下的内波特性，还需要进行系统的理论分析，以提高海洋内波的模拟精度。与静压近似下的动力学模型不同，本文根据N-S(Navier-Stokes)方程组，通过单独考虑非静压项，导出了能够更加符合实际观测的非静压海洋内波动力学模型。在模拟计算过程中，采用了曲线坐标进行了该模型的数值计算，模拟分析了双海脊海底结构对内波生成和传播的影响。为了对比第2个海脊在动力学过程中起的作用，在底边界处理上采用与Vlasenko相类似的处理方法，即分别考虑加入和去掉海脊的情况。通过分析并与目前文献中类似结果的对比，说明应用基于N-S方程的非静压海洋内波动力学模型处理复杂地形条件下的内波生成和演进问题的可行性和有效性。

1 非静压海洋内波模型

在以往大尺度海洋环流模式的研究中，采用静压近似是一种通用做法(如POM模式)。这样处理的优势在于分析的简化和计算的效率，并且其合理性符合大尺度环流模型，针对的是海洋中水平尺度远远大于垂向尺度的假设，而静压平衡对大尺度下的假设是近似成立的。但是在处理海洋内波等中小尺度或区域尺度的海洋动力学问题中，伴随着较强的水体垂向混合，非静压近似是必须考虑的重要条件。不仅如此，正如Mahadevan等在研究区域性海洋模拟[6]中的见解，认为非静压条件的引入或许会有效克服区域模式开边界求解原始方程组过程中遇到的多种困难(主要是病态条件数)，甚至能够在无黏性项时保持计算的稳定。

这里根据N-S方程组，在笛卡尔坐标系中，采用Boussinseq近似条件以及忽略地转效应等情况下，并将压强项表示为非静压和静压两部分，并导出了非静压动力学内波模型。模型方程主要包括不可压缩条件、动量方程、质量输运方程和边界条件等。

·U=0

(1)

∂U∂t+(U·)U=-1ρ0Q-G·R

(2)

∂ρ∂t+(U·)ρ=·γhρ+∂∂zγv∂ρ∂z

(3)

式中,方程(1)为不可压缩条件,方程(2)表示动量守恒方程,方程(3)表示海水水体的质量输运方程。这里U=(u,υ,w)T,表示海水水体质点流速矢量;ρ0表示海水的参考密度,且为常数,ρ为密度扰动,且水体微元密度可以表示为二者之和;表示微分算符,上面的波浪线表示微分只作用于水平方向。G为含有重力加速度g的三维矢量并表示为(g,g,0)T,R为水体的斜压部分,表示为1ρ0ρdz。显然,为考虑非静压对内波的影响,将压力场分解为静压和非静压两部分,其中Q表示为非静压场部分。由于该项是扰动密度场引起的压力场变化,也称为斜压项,且隐含密度场水平梯度变化,这一处理方法,使得在计算中能够精确得到并分析非静压场的影响。另外,νh和νv为水平和垂向的运动粘性扩散项,γh和γv表示质量扩散项。该方程能够从非静压角度较好地模拟海洋内波生成与传播。

在海洋内波研究中,水体表面边界一般采用刚盖近似,这种近似引入的原因可以从恢复力角度分析。在海洋水体内部,最初引起波动(如内潮波)的恢复力是一种约化重力,可表示为-Δρ/ρ0g。注意到海水次表层界面厚度远大于海洋的海气界面,因而相同大小的扰动力,在次表层引起水体波动的振幅要比在表层引起海面形成海浪的振幅要大得多。但是在海水表层,这种约化重力已趋于零,因而在海洋内波研究中多将上边界条件用刚盖近似表示。研究中,采用了海面(z=0)刚盖近似边界条件,表示为

∂Uh∂zz=0=0,∂w∂zz=0=0

(4)

海底为z=-H(x,y),采用了Manning-Chezy形式的边界条件[7],并表示为

νv∂Uh∂zz=-H(x,y)=μbUh,νv∂w∂zz=-H(x,y)=μbw

(5)

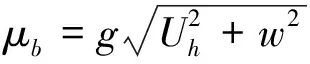
2 海底地形与海水跃层结构

2.1 双海脊海底拓扑结构

海脊地形对内波的影响极为显著,其中海脊的相对高程、海脊的斜率变化是影响内波生成、传播的重要因素。Vlasenko等[8]曾应用早期的MITgcm模型对陆架坡地形进行了研究,采用了不连续的坡折结构,Venayagamoorthy等[9]在实验室条件下研究了地形引起的内波破碎问题,地形采用了缓波结构。为了进一步揭示复杂海底地形对内波生成和演进的调制作用,这里应用了高斯函数设计了具有2个海脊的海底地形拓扑,并表示为

H(x)=H0-∑Nm=1Asmexp-(x-xsm)22σsm

(6)

式中,m=1,2,…N,Asm为海脊的高度H0为最大水深,σsm称为扩展参数。扩展参数一般可以取一个较大的数,同时表示地形的变化,并可以估计地形变化所示的一个近似斜率。当N等于2时,表示该海脊地形为双海脊拓扑结构。

2.2 海水密度跃层结构和初始场条件

对于密度跃层的变化,这里采用了一种双曲正切函数的形式[2]。为了反映入口处水体密度随特定潮流周期的变化而变化,在函数中加入了反映潮流的函数,并写为

ρ(0,z,t)=-Δρ2ρ0tanh[5.52*(z+d0-ξ(0,t))]

(7)

式中,Δρ和ρ0分别表示密度扰动的背景密度,d0表示密度跃层的中心位置,潮流函数表示为ξ(0,t)=∑ni=1aicos(kix-ωit),这里ai,ki和ωi分别表示各分潮的振幅、波数和频率。在下面的计算中,统一设定周期为120分钟,且n=1,即假设只有一个分潮存在。

3 计算结果及其分析

应用以上非静压海洋内波模型,结合初边值条件,分别计算了第2个海脊具有不同深度参数和扩展参数条件下的内波生成和传播过程的相关结果。为了突出第2个海脊的作用,在计算条件的设置上,令第1个海脊的参数固定不变,并设为海脊高程As1为60 m,扩展参数σs1为1.0×104;而第2个海脊参数设置为6种情况(如表1所示),其中海脊深度指的是在海脊最浅处深度,分别设为100、80、60 m,并且在深度为60 m时,设扩展参数值分别设为1.0×103、1.0×104、1.0×105。对于表中的每一种条件,可以粗略估计海脊的斜率。表2中给出了对应于6种条件下的计算结果或参数。

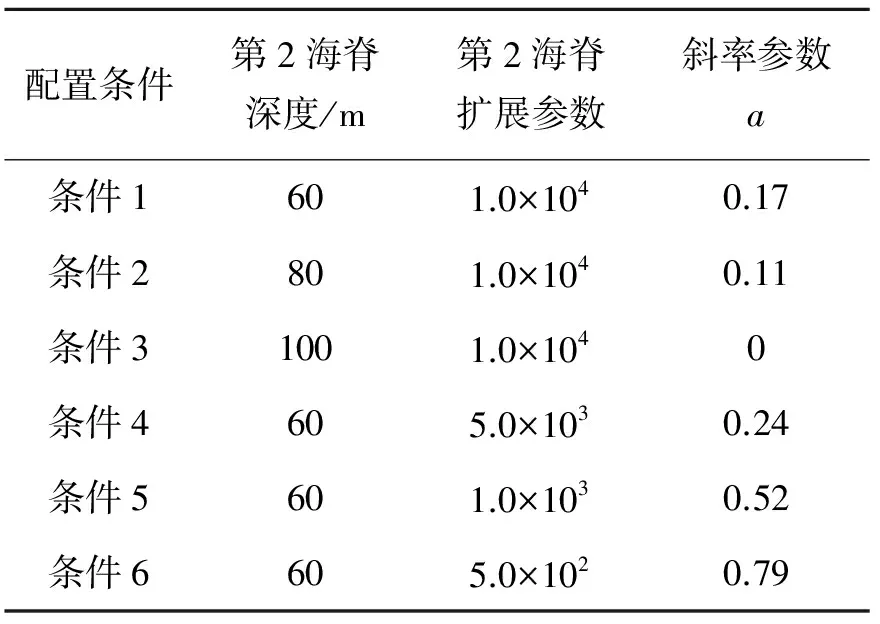
表1 第2个海脊的参数配置表

图1至图3分别是在“条件1、2、3”情况下,模型时间达到60、150和180分钟时的密度扰动结果截图。图4给出的是“条件4、5、6和条件3”时,模型时间为170分钟时的结果。图5给出了图2所示情况对应的相对涡度等值线图。

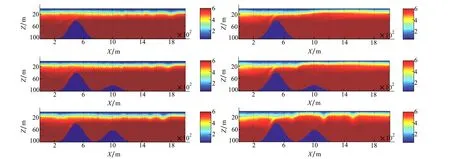
图1 具有不同深度条件下内波生成与传播示意(模型时间60分钟) 图2 具有不同深度条件下内波生成与传播示意(模型时间150分钟)

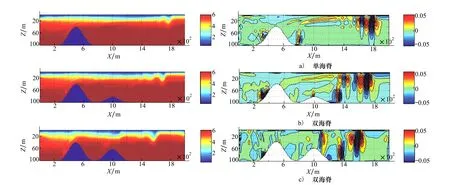
图3 具有不同深度条件下内波生成与传播示意(模型时间为180分钟) 图4 不同深度条件下的相对涡度变化示意图

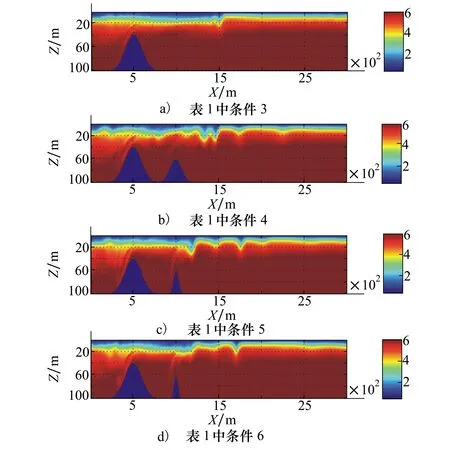
图5 不同扩展参数条件下内波生成与传播示意(模型时间170分钟)

由图1至图3可以看出,在模型时间为60分钟时,3种配置条件均产生了一组内孤立波列;在模型时间达到180分钟时,可以看出不仅产生了第2个内孤立波,而且还伴随着前一海脊产生的第2组波列与第2个海脊之间的相互作用,以及由此生成的第3组内波波列。并且产生的孤立波对应的时间及周期与潮波参数有较强的相关性。

由图4给出模型时间为180分钟时的相对涡度等值线图,进一步说明了第2个海脊在内波生成过程中的作用。进一步比较图中相对涡度强度变化可以看出,在相同模型时间下,相对涡度强度分布的位置明显不同,且有在第2个海脊存在时,b)和c)在海脊右侧下方的相对涡度均比无第2海脊a)的情况大。由相对涡度强度分布位置的不同进一步说明了内孤立波形成和传播过程与第2海脊的相关性。

根据图5给出在条件3、4、5和6情况下的结果可以看出,在模型时间为171分钟时,波列形态存在的差异。比较a)和d)的结果,反映出第2组波由第1海脊产生后,还存在明显的 “下陷”,并且由于第2海脊的影响,最后生成了伴随第2组波(图中右边箭头)且比其更强的孤立波。由此后的演进结果(未画出)表明,图中左边箭头所指示位置将发展成伴随于第2组波列后的孤立波(列),并且由于该波的强度明显大于原来的第2组波,在发展过程中,这一伴随波能够超过原第2组波。这说明在有两海脊存在的条件下,可能存在“快波”和“慢波”的情况,这与Alford[1]的数据分析南海北部海域的内波演进过程中所谓“A-B波”的情况吻合。另外从图中b)和c)与d)的比较可以看出,第2个海脊参数的变化,使“快波”和“慢波”出现“叠加”,并使内波的形态变得复杂;同时从表3计算的伴随波(即后面的快波)与原激发波(原第2组波)的速度也说明了双海脊条件下“快波”和“慢波”速度的差异。

根据模型计算的内波形成和传播整个过程,可以从孤立波传播时间和强度方面,进一步给出双海脊结构对内波影响的定量结果。通过记录第1个、第2个孤立波形成时间点,并由扰动密度的等值线变化,提取了内孤立波到达某一位置处的强度(振幅)信息。表2给出了表1对应条件下的计算结果,其中位置A对应的是水平方向1 500 m所在的位置,位置B对应的是2 000 m处,位置C对应的是水平3 000 m所在的位置。

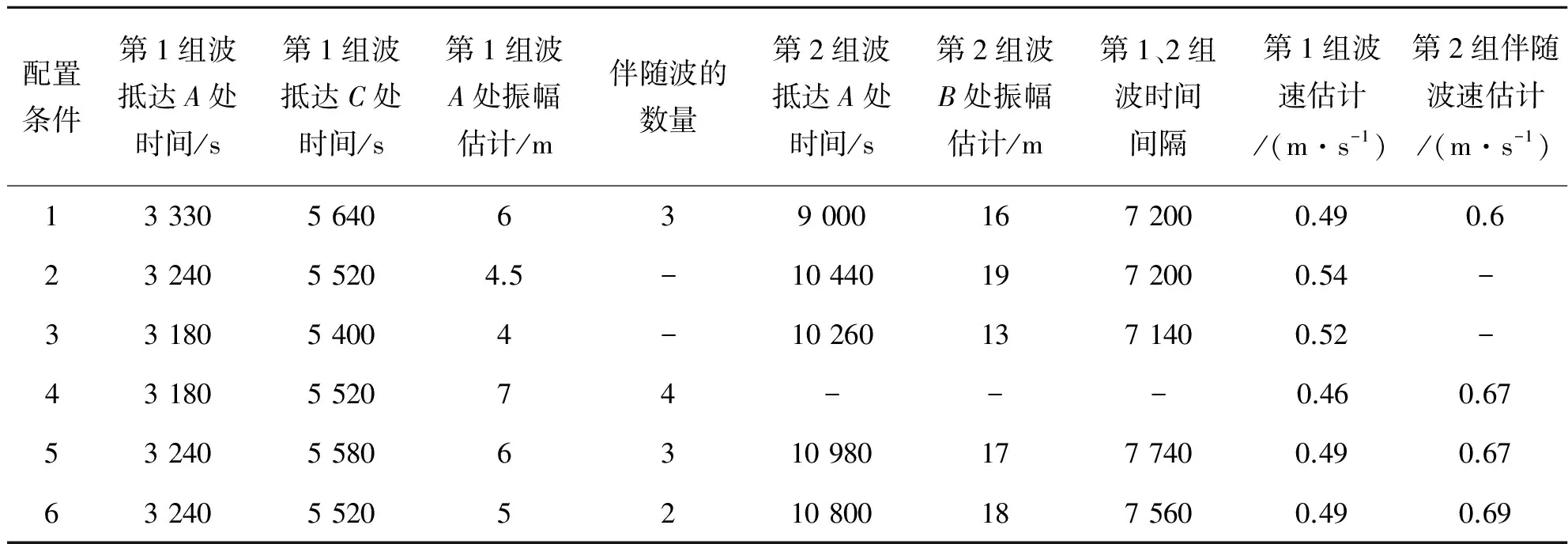
表2 第2海脊地形参数变化时的计算结果

结合表2对应条件1、2、3给出的结果，可以看出，当存在第2个海脊时，生成内孤立波到达A或到达C处的时间明显延长，而且形成的内波振幅明显大于无第2个海脊的情况。这说明双海脊的存在特别是第2海脊的存在，对于内波的生成和强度均有较为明显的影响作用。

根据表2中条件4、5、6和3，分析海脊坡度变化对内波抵达时间和强度计算结果的影响，可以明显看出第2个海脊坡度对内波形成的作用。坡度越大形成下陷的时间可能更长，这说明在能量“积聚”阶段持续的时间更长，但也预示着产生更大的“下陷”和生成强度更大的内孤立波。

第2个海脊减缓了内孤立波的生成时间，且减缓的程度与第2海脊的高度有关，深度较浅时可能的阻截时间更长，即具有较浅的第2海脊的情况，调制作用更大。进一步结合图3c)在达到180分钟时，可以看出不仅生成了第2个孤立波列，并使存在的2个波列可能形成叠加的效应，进而形成强度更大的孤立波(列)。

由以上分析我们可以得到如下初步结论：①潮流与地形相互作用形成的“下陷”是内孤立波生成的重要影响因素；②双海脊的存在，减缓了内孤立波生成时间，且与第2个海脊高度有关，深度较浅时可能阻截时间更长；③第2个海脊的坡度与内波生成有密切关系，并可能影响第1海脊形成的下陷；④双海脊存在时，当第2海脊高程小于第1个海脊时，2个海脊可能都会形成下陷，并且在演化过程中，第1个海脊形成的“下陷”在第2个海脊影响下能够形成更大孤立波，并且传播速度高于第1个，表现出“快波”在后追赶“慢波”的情况。

4 结 论

基于动力学模型是海洋动力学物理过程的近似这一基本原理，考虑到非静压在中小尺度海洋动力学研究的重要作用，在海洋动力学理论分析基础上得到了非静压海洋内波模型。以此为基础对双海脊海底地形条件下，海洋内波生成与演进过程进行了数据模拟计算研究。通过分析双海脊地形参数的变化对密度场扰动、相对涡度变化以及内孤立波列的先导波抵达时间、强度等定量结果及变化，揭示了双海脊地形对内波生成和演进的一般规律。

研究认为，在内波多发区，具有双海脊存在的海底地形，对内孤立波的生成时间、传播速度和强度均造成了较强的调制作用或影响。相较于单海脊的情况，在内波的形成的初期，第2海脊的存在减缓了内孤立波的生成时间，并且这一作用的强弱，受海脊水深和坡度影响。双海脊的存在使得这些内波特征要素的规律性变得更为复杂，但是通过合理设置地形特征，能够有效模拟内孤立波的生成和演进过程。因此，通过非静压海洋内波动力学模型研究海底地形拓扑结构对内波的影响，特别是多海脊的海底地形结构对其生成和演进的定量计算和分析，对于揭示海洋内波的生成和传播规律及内波的监测或预报具有重要价值。

参考文献：

[1] Alford M H, Lien R C, Simmons H, et al. Speed and Evolution of Nonlinear Internal Waves Transiting the South China Sea[J]. Journal of Physical Oceanography, 2010, 40: 1338-1355

[2] Guo C, Chen X, Vlasenko V, et al. Numerical Investigation of Internal Solitary Waves from the Luzon Strait: Generation Process, Mechanism and Three-Dimensional Effects[J]. Ocean Modelling, 2011,38:203-216

[3] Ramp S R, Yang Y, Bahr F. Characterizing the Nonlinear Internal Wave Climate in the Northeastern South China Sea[J]. Nonlinear Processes in Geophysics, 2010, 17: 481-498

[4] Xu Z H,Yin B S, Hou Y J. Highly Nonlinear Internal Solitary Waves over Continental Shelf of Northwestern South China Sea[J]. Chinese Journal of Oceanology and Limnology, 2010, 28(5):1049-1054

[5] Vlasenko V, Guo C, Stashchuk N. On the Mechanism of A-Type and B-Type Internal Solitary Wave Generation in the Northern South China Sea[J]. Deep-Sea Research I, 2012, 69 : 100-112

[6] Mahadevan A, Archer D. Modeling a Limited Region of the Ocean[J]. Journal of Computational Physics, 1998, 145:555-574

[7] Casulli V, Cattani E. Stability, Accuracy and Efficiency of a Semi-Implicit Method for Three-Dimensional Shallow Water Flow[J]. Computers Math Appliciation, 1994, 27(4):99-112

[8] Vlasenko V, Hutter K. Numerical Experiments of the Breaking of Internal Solitary Waves over Slope-Shelf Topography[J]. Journal of Physical Oceanography, 2002, 32: 1779-1793

[9] Venayagamoorthy S K, Fringer O B. Numerical Simulations of the Interaction of Internal Waves with a Shelf Break[J]. Physiscs of Fluids，2006,18(7): 076603

[10] Fringer O B, Gerritsen M, Street R L. An Unstructured-Grid, Finite-Volume, Nonhydrostatic, Parallel Coastal Ocean Simulator[J]. Ocean Modelling,2006,14:139-173