移动荷载下高速铁路路基应力主轴空间旋转效应及规律

薛富春，张建民

(1.重庆交通大学 土木工程学院，重庆 400074；2.清华大学 土木水利学院，北京 100084)

自2003年10月我国第一条准高速铁路秦沈客运专线开通运营以来，高速铁路在我国迅速发展，截至2015年年底，高速铁路运营总里程达到1.9万km，占全球高速铁路总里程的60%以上。与中低速和普速铁路相比，高速铁路列车的运行在基础结构中引起的动力效应明显增强，其结果之一是造成基础结构疲劳、损伤甚至累积变形，对基础结构的服役周期产生不利影响。以路基为例，我国高速铁路路基上的轨道及列车荷载被一定分布的均布荷载代替[1]，属于静力学范畴，难以反映路基实际动态工作情况。文献[2]研究指出，列车荷载不能简单地换算成一定分布宽度和高度的土柱，不宜作为(准)静态问题来对待。

在反复荷载如地震荷载、波浪荷载和交通荷载作用下，结构中的主应力状态既有大小变化又有方向变化，即存在着明显的应力主轴旋转效应[3-4]。文献[5]认为波浪荷载属于非比例循环加载，其会导致海床土体主应力轴旋转，使海床的累积变形、孔隙水压力增长特性及抗液化强度明显变化。高速列车移动荷载在基础结构中引起的动力学行为是多方面的，其中应力主轴的空间旋转效应是非常重要的特征，现场测试也证实了这种现象的存在[6]。国内外学者开展过相关研究工作，文献[7-10]将列车荷载简化为一系列移动点荷载，将列车-地基相互作用简化为弹性半空间-Euler-Bernoulli梁模型，引入弹性半空间等效刚度的概念，对列车移动荷载引起的地基动应力进行研究。文献[11]采用2.5维有限元建立轨道-路堤-地基耦合分析模型，推导了地基中动应力的半解析解答，剖析列车轮轴荷载作用过程中地基内部土单元体的应力路径和其中的应力主轴旋转现象。文献[12]基于Boussinesq课题解答，利用集中荷载作用下半无限空间弹性路基中不同空间位置且满足一定限制条件的点的应力应变状态集合，来表征单次行车荷载下路基岩土体内某一点加载、卸载全过程的应力、应变等力学响应，将动力学问题转化为准静力学问题，探讨了路基在一个加载、卸载全过程的应力状态及其有效作用半径。文献[13]将地下铁道列车动力荷载看成多个移动的轮轴荷载，根据弹性半空间的Mindlin问题解答，分别以单个轮轴荷载和列车移动荷载为例，研究地铁荷载作用线正下方地基土中的动应力特征、应力路径变化及应力主轴旋转，分析了不同埋深情况下荷载作用线正下方土单元应力状态的变化。

针对交通荷载引起的应力主轴旋转效应，已有研究已取得了一定成果，但也存在一些问题，主要是分析模型过于简化，如将轨道-路基-地基简化为铺设在半无限空间的梁，客观存在的材料非线性、接触状态非线性和动荷载作用前的静应力场对动力分析的影响、列车引发应力波的传递等因素均未考虑，造成结果失真甚至出现错误。

列车运行在轨下基础中引起的动力学响应较复杂，这一动力学初值、边值问题涉及材料非线性、接触状态非线性和几何非线性，在目前技术水平下，几乎不可能求解该系统动态响应的解析解。在此背景下，作为前期探索，本文基于多尺度和精细化建模技术，构建直线段上高速铁路轨道-路基-地基非线性耦合动力分析模型，依托高性能并行计算，研究移动荷载作用下高速铁路路基中应力主轴的空间旋转效应及其规律，为研究列车微振幅低应力荷载作用、低频率超长周期加载、温度与湿度的交替变化等因素耦合作用下路基的累积变形提供依据。

1 构建动力学分析模型

1.1 模型概况

根据设计资料，构建设计时速350 km的直线段上双线高速铁路路基真三维耦合分析模型，如图1所示。模型沿线路方向长度为450 m，路基高度为7 m，顶面宽度为13.6 m，底面宽度为34.3 m，地基最大宽度为120 m。整个模型节点数为4 749 192，单元数为3 298 489，自由度数为14 132 724。

(a)钢轨、轨枕和轨道板网格

(b)分析模型局部视图(一)

(c)分析模型局部视图(二)

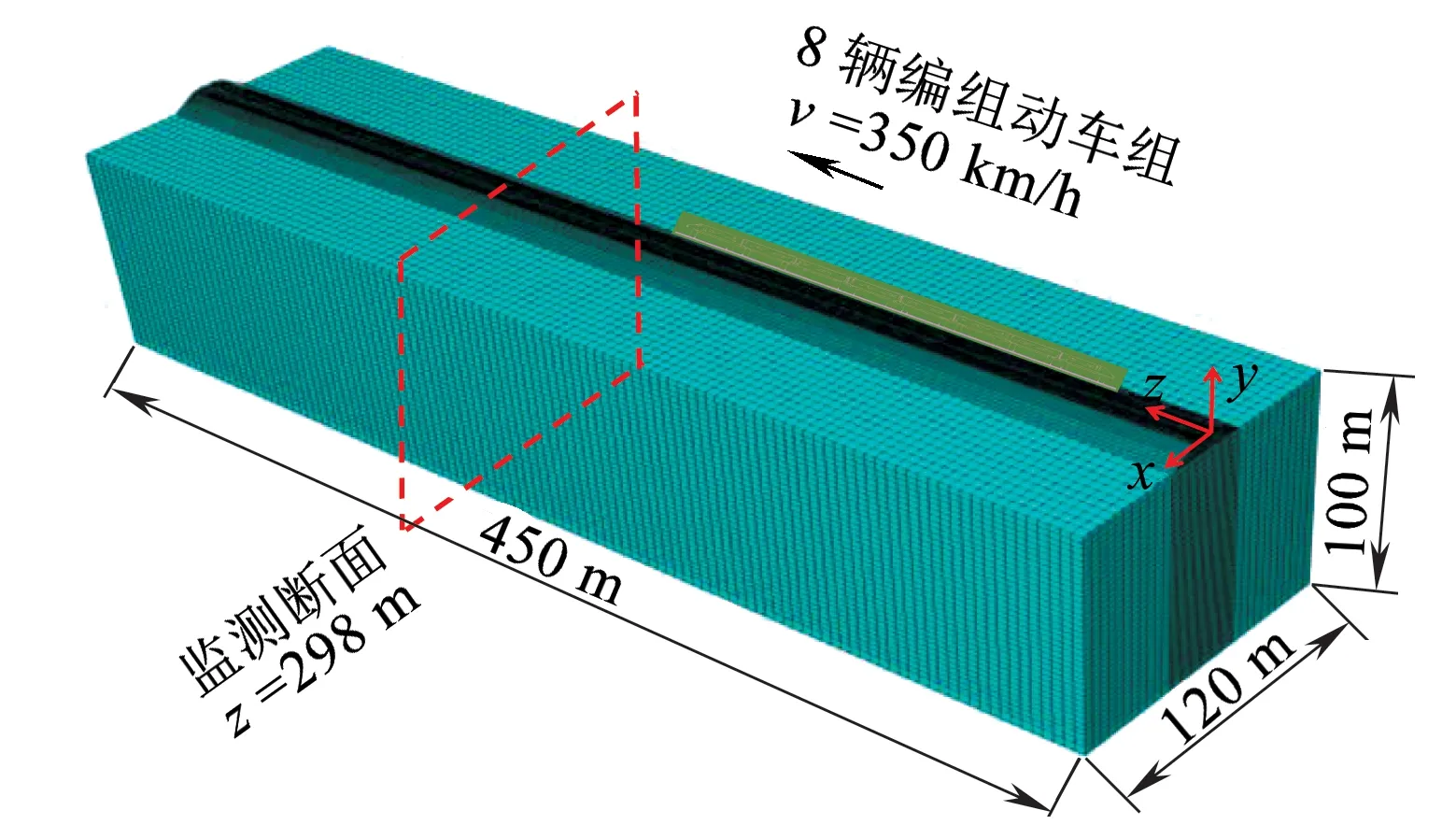
(d)整体分析模型及选择的监测断面位置概况图1 分析模型有限元网格划分

1.2 模型参数与材料本构关系

场地岩土参数、轨道系统参数与路基各部分参数见表1～表3，在移动荷载有限次作用下，场地土体和路基可采用Drucker-Prager本构模型模拟，文献[14]表明对轨道系统采用线弹性本构模型模拟是合理的。

1.3 动力荷载与边界条件

计算中采用的荷载位置，与某型动车组轮对在空间上的位置一一对应，为降低难度，本研究通过在钢轨表面施加压力模拟轮轨动力相互作用，以脉冲函数表示

p(t)=Psin2(2πft)

( 1 )

式中：p为接触斑上的压力；P为接触斑上的最大压力；f为荷载作用频率。

表1 土体参数

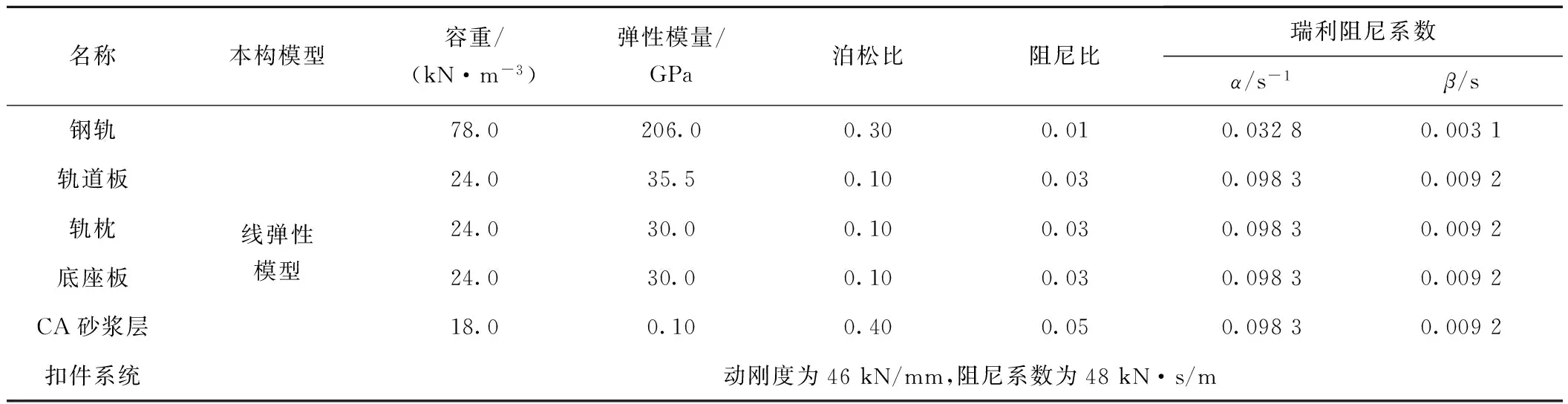
表2 轨道系统参数

表3 路基参数

根据文献[14]，将作用于钢轨最上部单元顶面的压力荷载幅值取为P=96.36 MPa。

高速铁路路基支撑在地基上，而地基是从无限域中取出的有限部分，因此，受计算能力限制，分析模型需要采用人工边界模拟无限地基。由于移动荷载作用是在路基填筑、轨道系统铺设完成后进行的，因此必须考虑静应力场对动力分析的重要影响[14]。

1.4 分析顺序

分析顺序与施工过程一致，包括地基初始地应力场的生成、路基的分层填筑、轨道系统铺设及移动荷载作用过程共四个阶段，其中前三个阶段为静力学分析，第四个阶段为隐式动力学分析。

2 结果与分析

为获得高速铁路路基中单元动应力的时间历程，计算前在z=298 m断面选取典型单元，如图2所示，断面的相对位置如图1(d)所示。

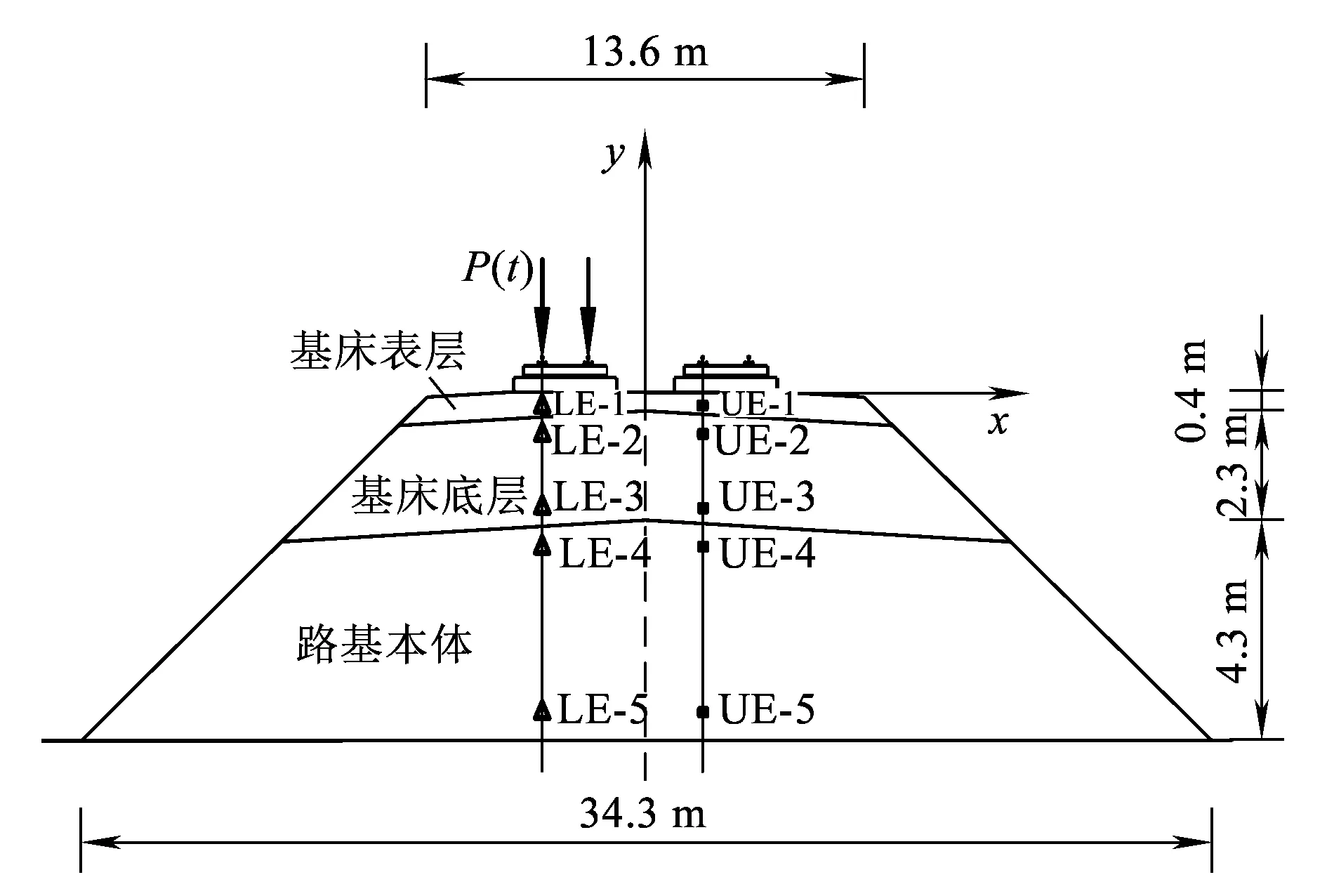
图2 路基中选取的单元位置

2.1 受载钢轨正下方单元的应力主轴旋转

在荷载移动过程中，上行线受载钢轨之一正下方不同深度位置单元LE-1～LE-5，其应力主轴的空间旋转如图3所示。

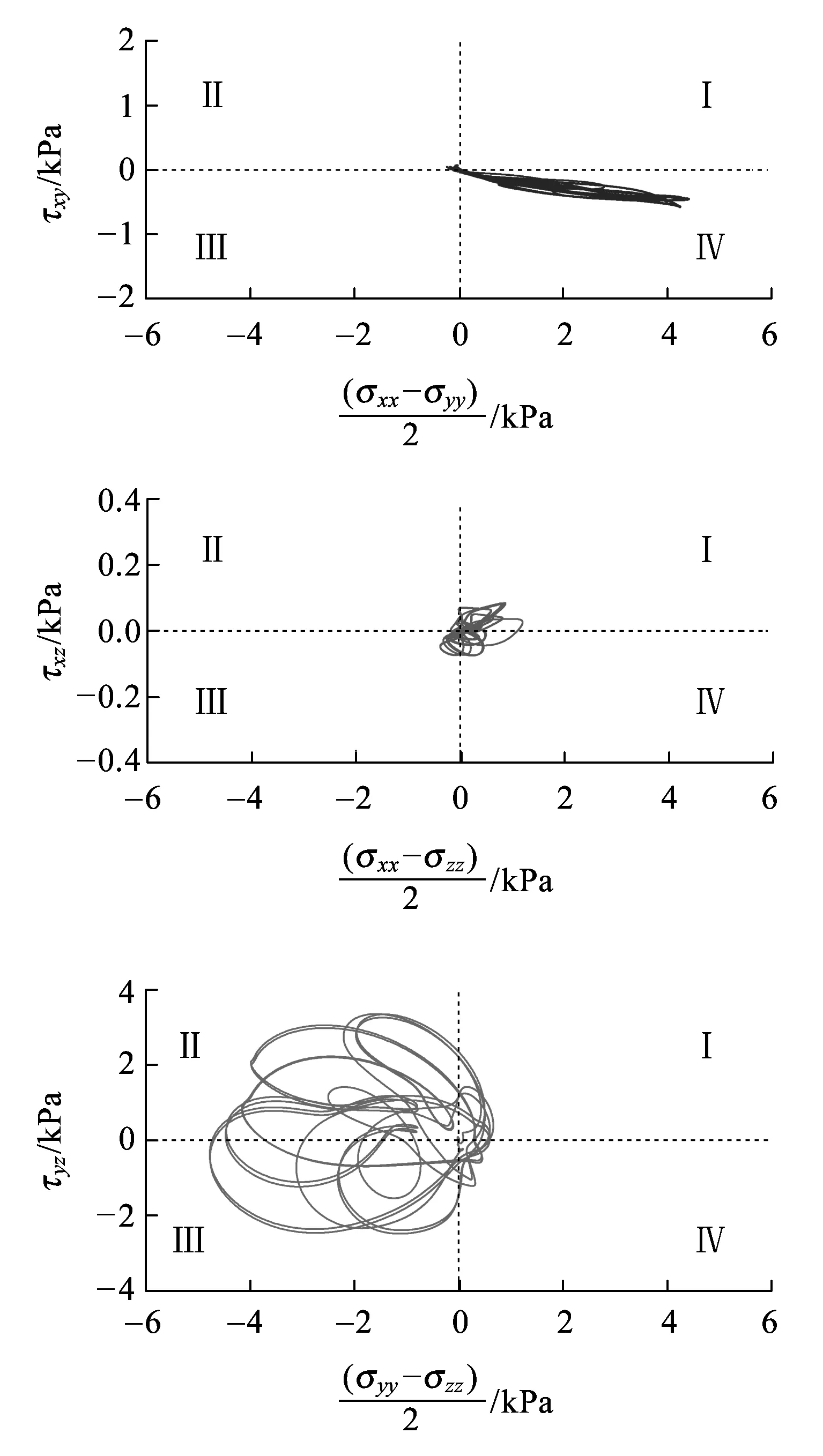
(a)基床表层LE-1单元

(b)基床底层表面LE-2单元

(c)基床底层底面LE-3单元

(d)路基本体表面LE-4单元

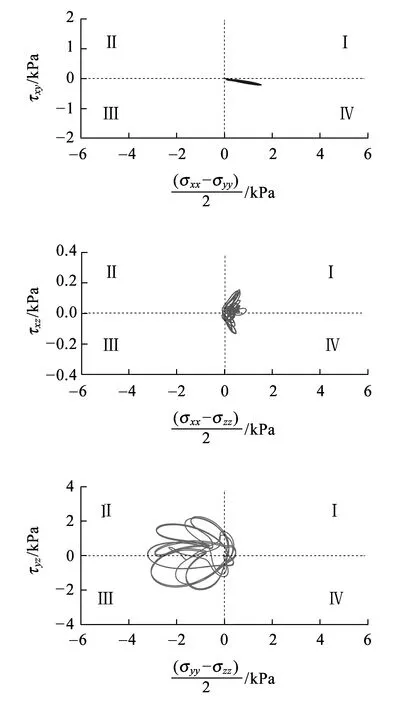
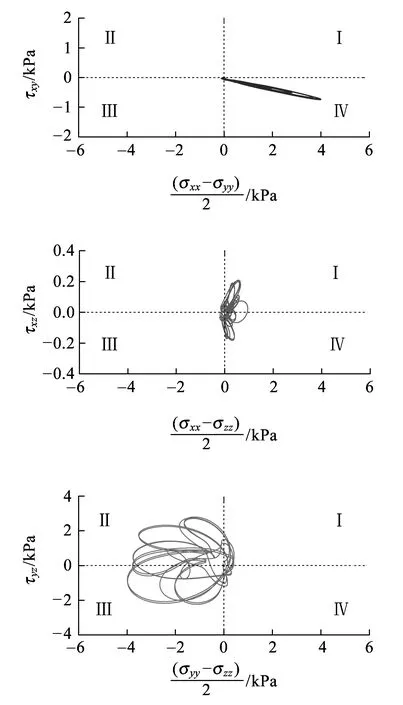
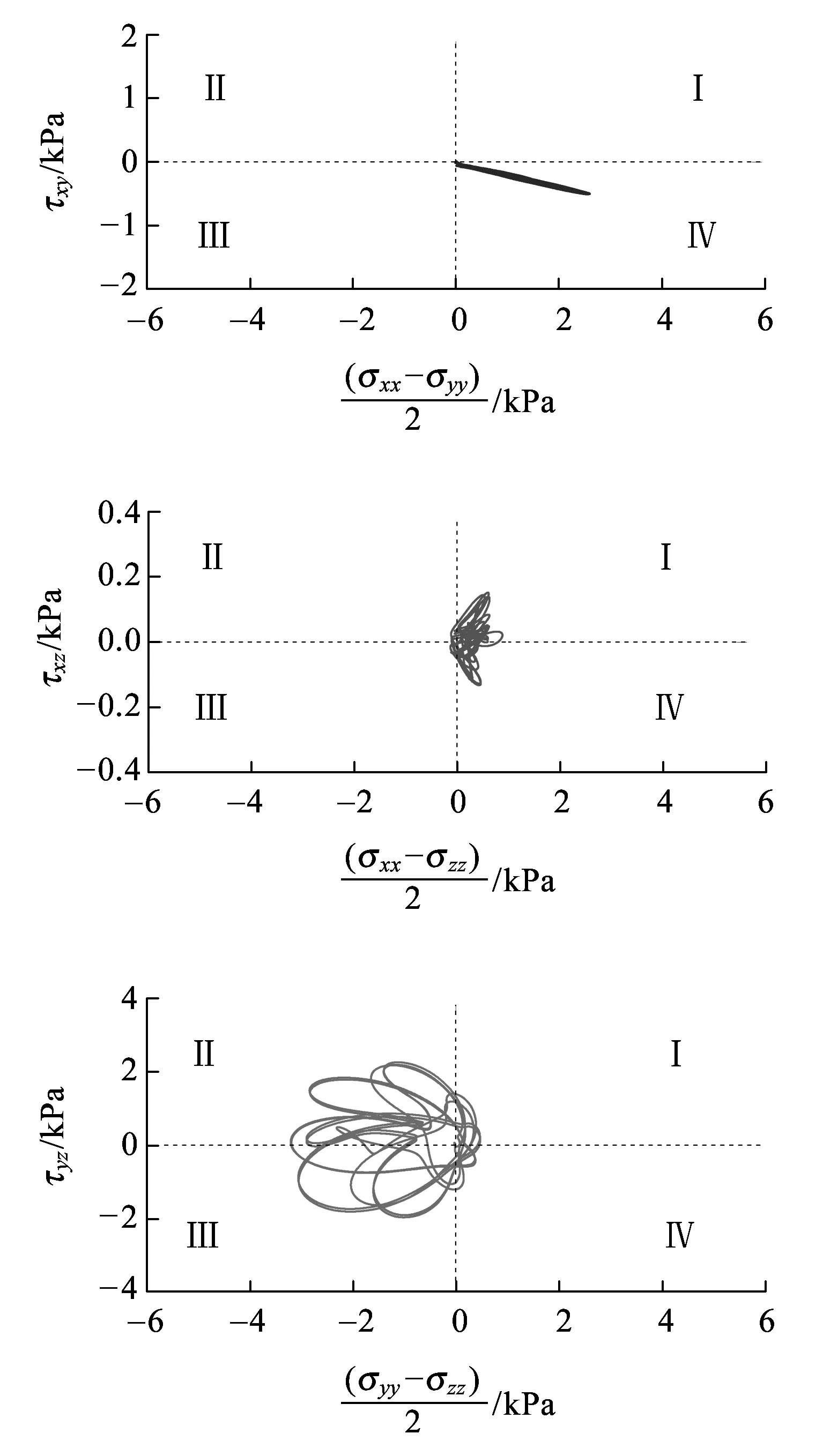
(e)路基本体底面LE-5单元图3 受载钢轨之一正下方单元的应力主轴旋转

图3显示，在32个荷载通过所考察单元的过程中，由于6个应力分量均不为零，不同深度单元的应力主轴在xy、xz、yz平面内发生了同步、连续的旋转，以yz平面内的旋转为主，主要分布在区域Ⅱ、Ⅲ，其次是xy平面内的旋转，主要分布在区域Ⅳ，xz平面内的旋转最弱，主要分布在区域Ⅰ、Ⅳ。

在xy平面内，不同深度单元应力主轴的旋转模式具有相似性，强度随深度的增加而减小，yz平面内的旋转也有类似特点。xz平面内基床表层单元LE-1应力主轴的旋转模式明显与其他两个平面不同，该单元与荷载作用位置最近，但其旋转强度并非最大，其原因是基床表层表面与底座板底面之间、基床表层与基床底层之间接触面两侧介质的波阻抗相差较大，钢轨传递的应力波在这些界面会发生强烈、复杂的相互作用，并生成表面波。每个荷载的作用都会激发应力波，这些应力波相互干扰，在32个荷载作用下，基床表层附近的波场较复杂，因此基床表层单元的应力路径比深层单元的更复杂，没有明显的规律性。此外，应力波的相互作用具有“削峰”效应，相互作用后的应力波，其幅值在一定程度上被减弱，因此其旋转强度反而低于更深处的单元。

2.2 非受载钢轨正下方单元的应力主轴旋转

下行线非受载钢轨之一正下方不同深度位置单元UE-1～UE-5应力主轴的空间旋转如图4所示。

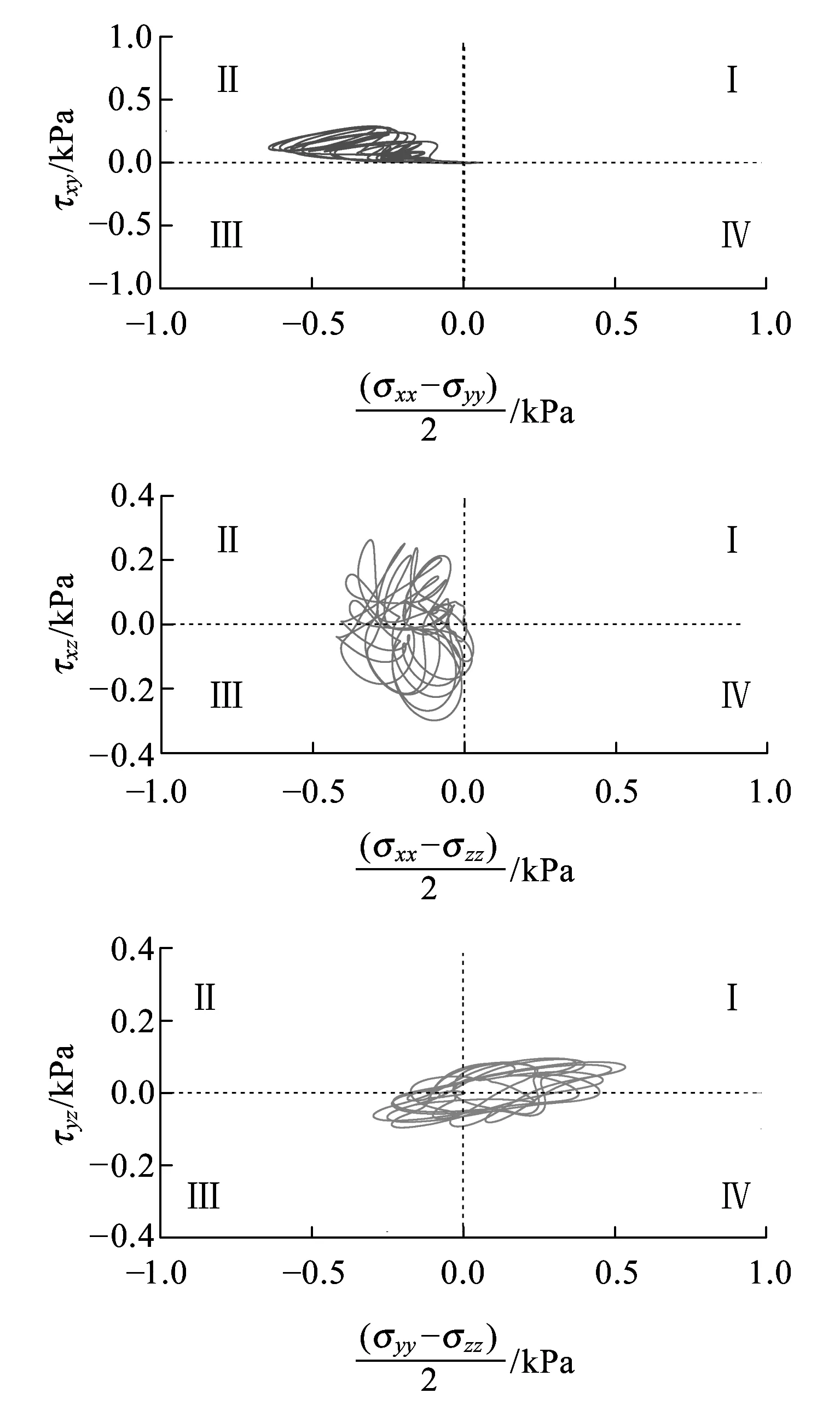
(a)基床表层UE-1单元

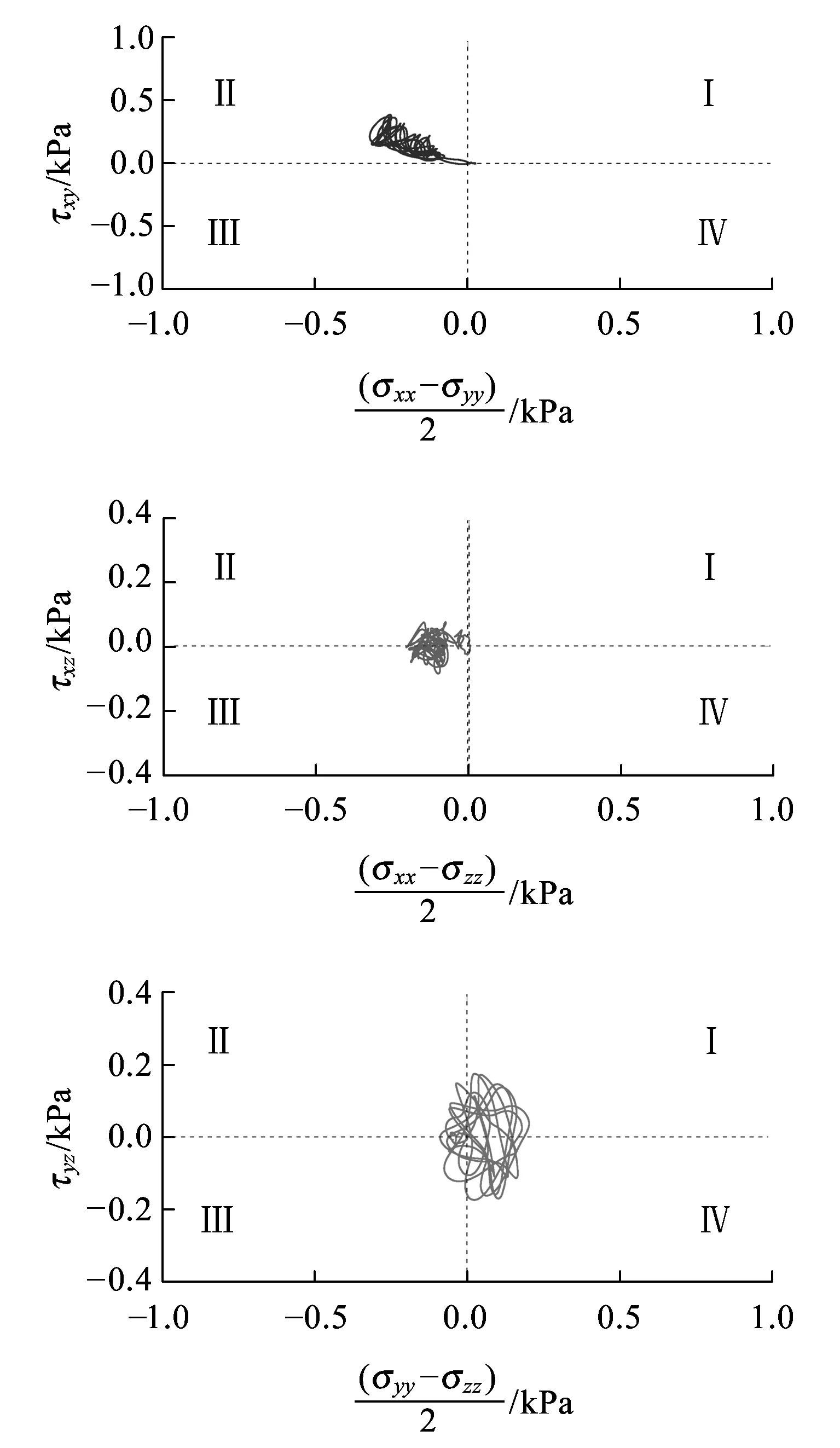
(b)基床底层表面UE-2单元

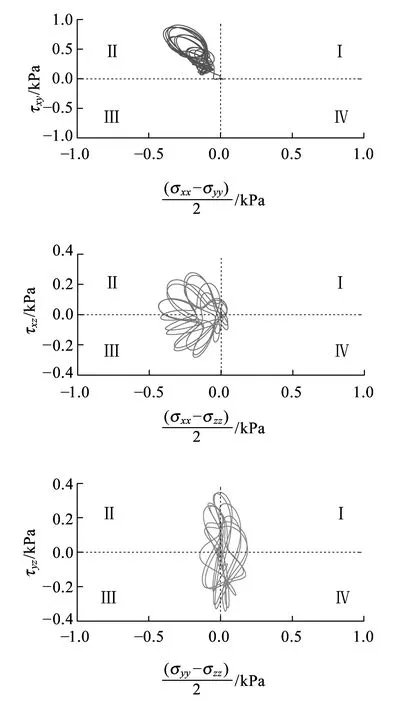
(c)基床底层底面UE-3单元

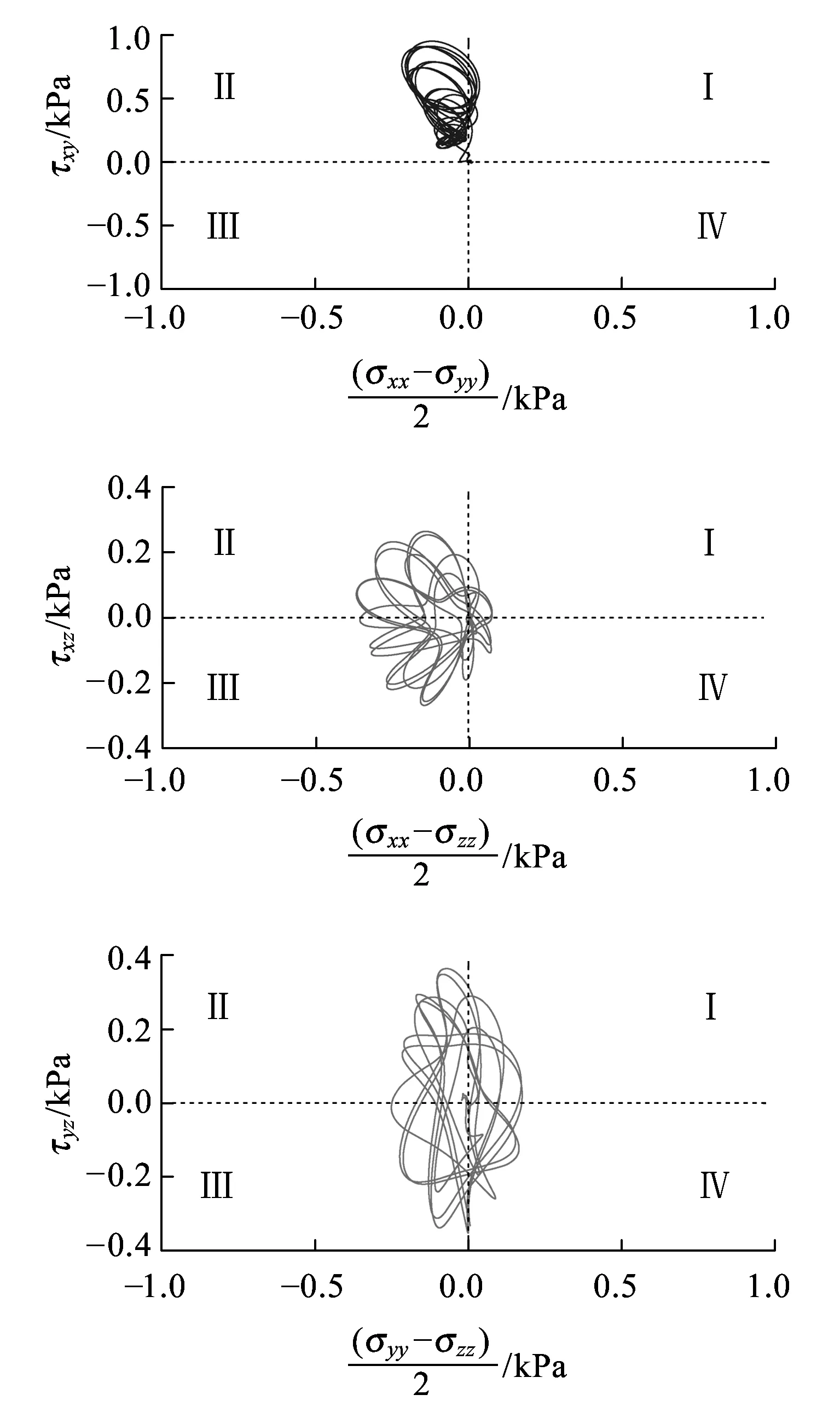
(d)路基本体表面UE-4单元

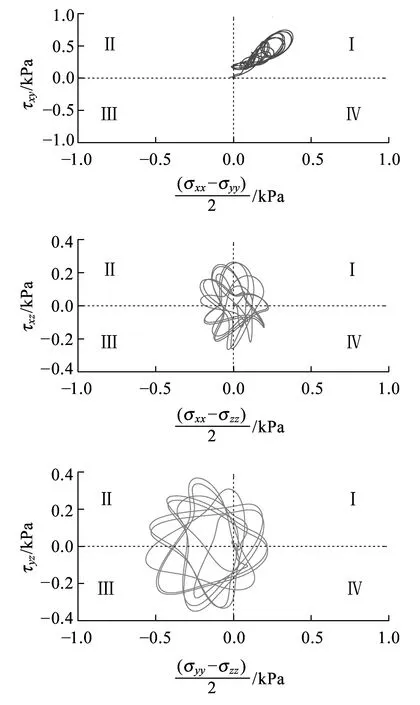
(e)路基本体底面UE-5单元图4 非受载钢轨之一正下方单元的应力主轴旋转

图4显示，在荷载移动过程中，所考察单元的应力主轴在xy、xz、yz平面内也发生了同步、连续的旋转。与受载钢轨正下方单元不同，非受载钢轨正下方单元的应力路径在xy平面内的旋转最强，在其他两个平面内的旋转强度较弱且相差不大。

与非受载钢轨正下方其他单元的应力主轴旋转模式相比，基床表层单元UE-1的旋转模式有明显差异，其原因与前述类似。

随着深度的增加，xy平面内应力主轴旋转模式和分布范围逐渐发生改变，从基床表层处的区域Ⅱ逐渐偏转到路基本体底面的区域Ⅰ；xz平面内的旋转从区域Ⅱ、Ⅲ逐渐向区域Ⅰ、Ⅳ偏转，yz平面内的旋转从区域Ⅰ、Ⅳ逐渐向区域Ⅱ、Ⅲ偏转。发生上述偏转的原因是在某时刻，非受载钢轨正下方不同深度单元与另一侧钢轨上所施加的荷载相对位置不同，各单元与所施加的荷载连线与竖直方向有不同的夹角，因此其应力主轴的旋转模式与位于受载钢轨正下方的单元不同。由于非受载钢轨正下方单元与另一侧荷载作用位置相对较远，荷载作用效应对其应力状态支配的地位有所降低，非受载钢轨受表面波影响程度却增大，这些因素的综合作用，使单元应力主轴的旋转出现了上述偏转特征。

3 地基表面直接作用移动荷载引起的应力主轴旋转效应

为了比较高速铁路路基中的应力主轴旋转与地基表面作用移动荷载引起的应力主轴旋转效应，本文在3.1节和3.2节给出在单相、各向同性地基表面直接作用一个移动恒载这一最简单情况下的动应力时程和应力主轴旋转效应。地基长度为450 m，宽度为60 m，深度为50 m，如图5所示。为保证计算精度，单元尺寸在z方向和y方向取为0.5 m，在x方向取为1.0 m，整个模型节点数为3 003 033，单元数为2 880 000，自由度数为9 009 099。

取100 kPa的恒定压力荷载，移动速度选取50.0 m/s和100.0 m/s两种，以考察移动速度对单元应力路径的影响。选取的单元位于加载面正下方0.5 m(单元1)和5.0 m(单元2)处(图5(a))，以考察不同深度处单元受表面波的影响程度。地基土参数见表4。

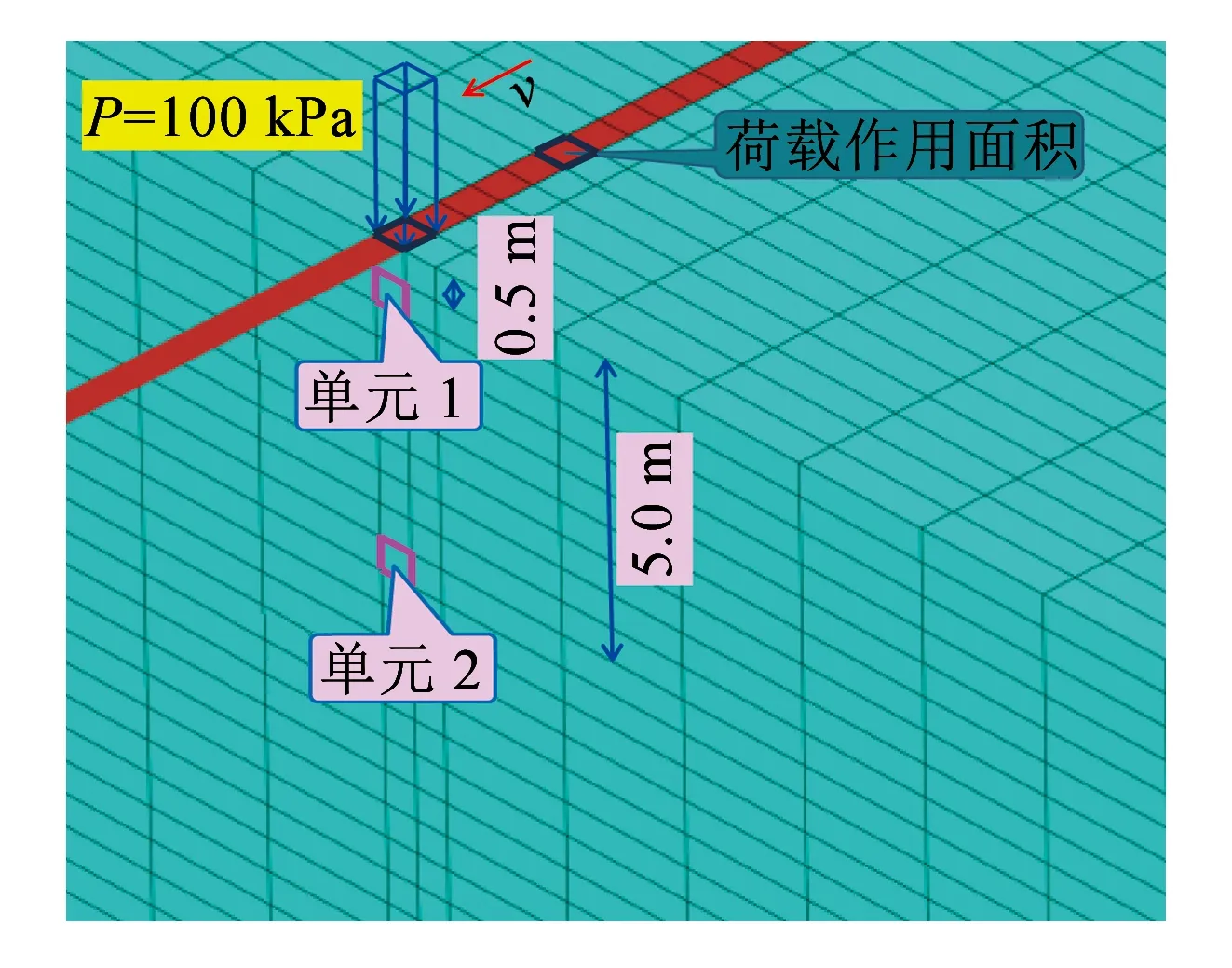
(a)荷载作用工况及选取的单元位置

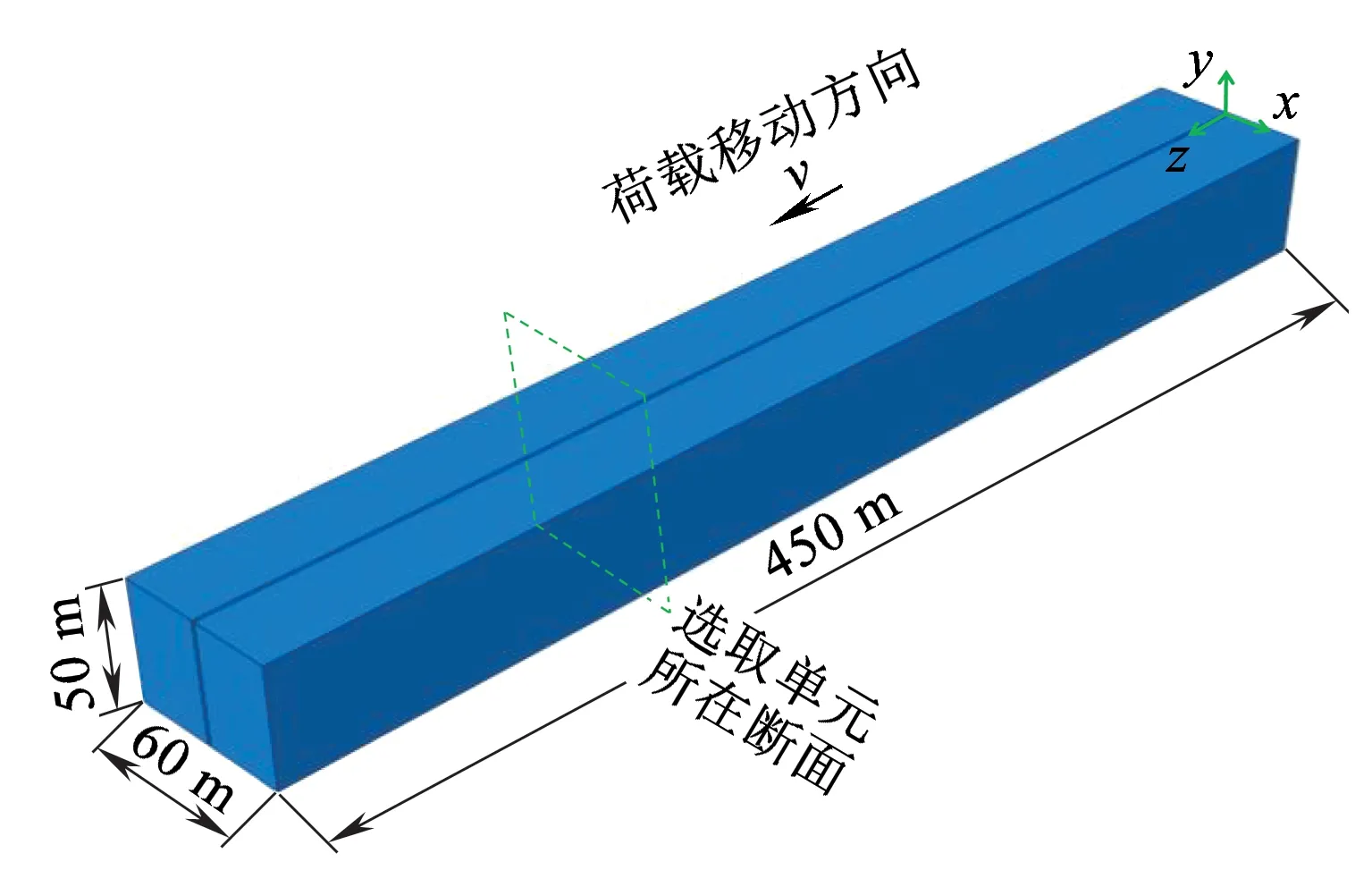
(b)整体模型图5 地基表面作用移动荷载计算模型

参数容重/(kN·m-3)弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)阻尼比瑞利阻尼系数α/s-1β/s取值18.020.00.326.8220.080.2390.010

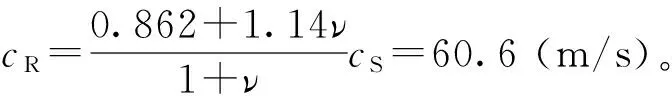
3.1 荷载作用面正下方单元的应力时程

荷载移动过程中，其作用面正下方0.5 m和5.0 m处单元的动应力时程如图6所示。

本例中荷载移动速度50 m/s工况的计算时间为8 s，在0～3 s和7～8 s时间段内，动应力基本为零，为便于与100 m/s工况(计算时间4 s)比较，只截取荷载移动速度50 m/s工况3～7 s的时程。

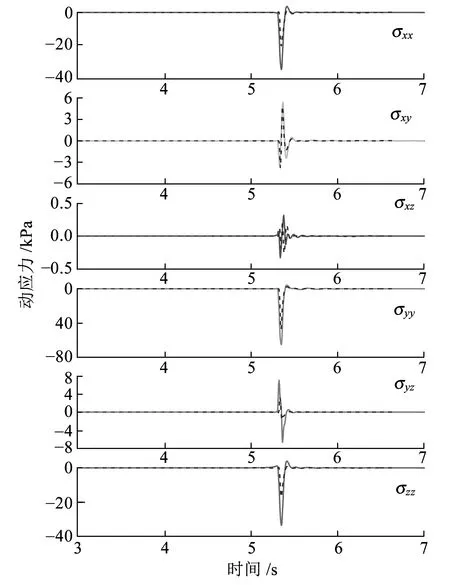
(a)0.5 m深度处单元1动应力时程

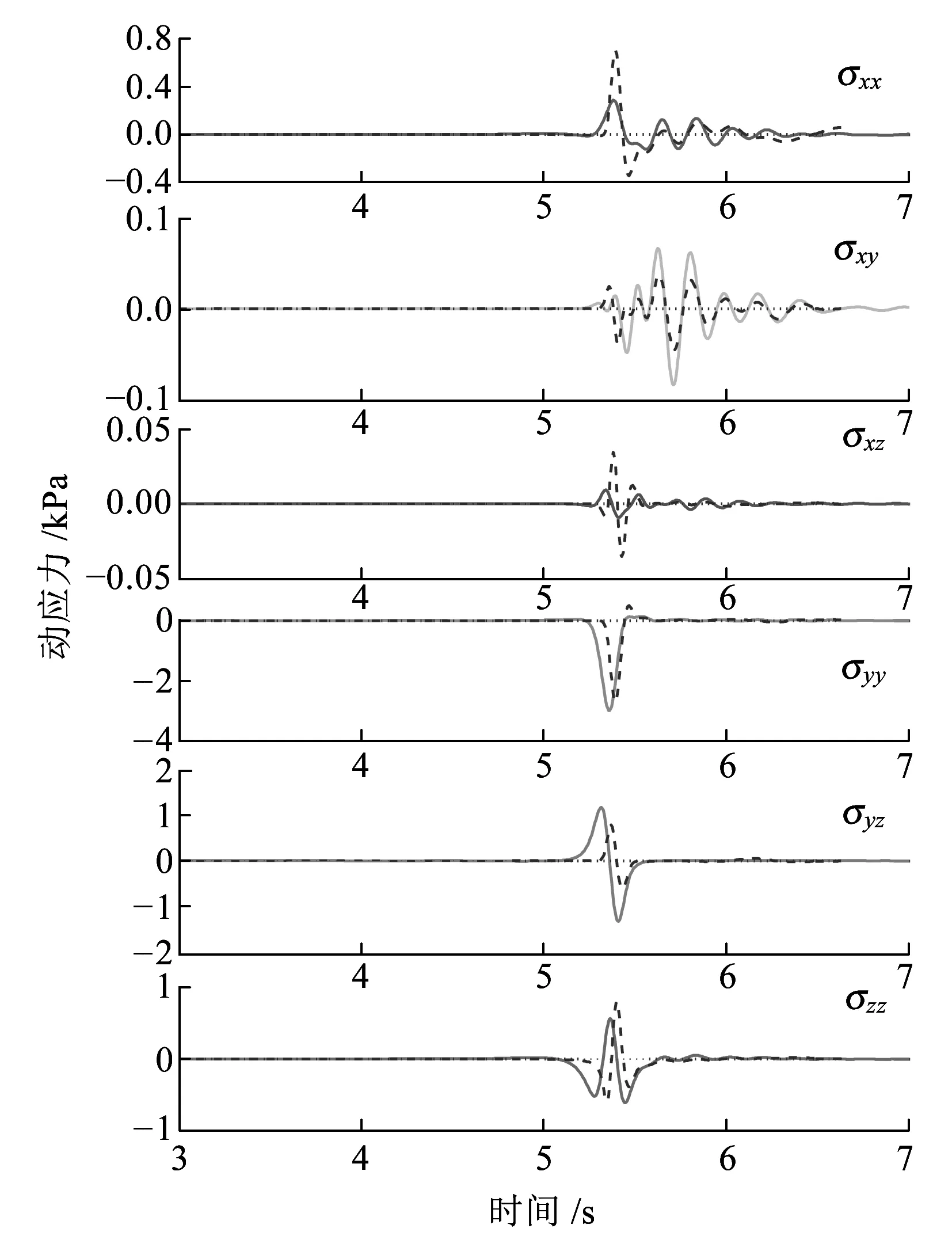
(b)5.0 m深度处单元2动应力时程

图6 不同深度单元动应力时程

图6显示，土体单元的6个动应力分量均不为零，尽管有的应力分量数值较小。从较浅的单元1动应力看，正应力基本上表现出轴对称特征，剪应力则表现出中心对称特征，在较深的单元2，动应力的对称性减弱。对于两个单元来说，在荷载通过该单元后，由于土的阻尼作用，其动应力不会立刻衰减为零，而是需要经历一段时间，这在图6(b)中表现得尤其明显，动应力的这种逐渐衰减过程是采用静力学方法所不能获得的。

不同移动速度下的动应力响应规律类似。接近地表处，低速移动下的动应力比高速下的动应力大，因为荷载移动速度为50 m/s，达到地基Rayleigh波速的82.5%，地基表层土体出现了一定程度的共振，引起的响应得到加强，高速移动(100 m/s)则远离地基Rayleigh波速，故其引起的响应反而较小。

3.2 荷载作用面正下方单元的应力主轴旋转

荷载作用面正下方0.5 m和5.0 m处单元应力主轴的空间旋转如图7所示。

图7显示，在荷载移动过程中，较浅的单元1和较深的单元2，其应力主轴在xy、xz、yz三个平面内发生了同步、连续旋转，在yz平面内的旋转强度最大，xz平面内最小。在较浅的单元1处，荷载移动速度为50 m/s引起的旋转强度均大于100 m/s的情况；在较深的单元2处，荷载移动速度为50 m/s引起的旋转强度在yz平面内大于100 m/s对应的结果，在其他两个平面内则要小于100 m/s对应的结果。

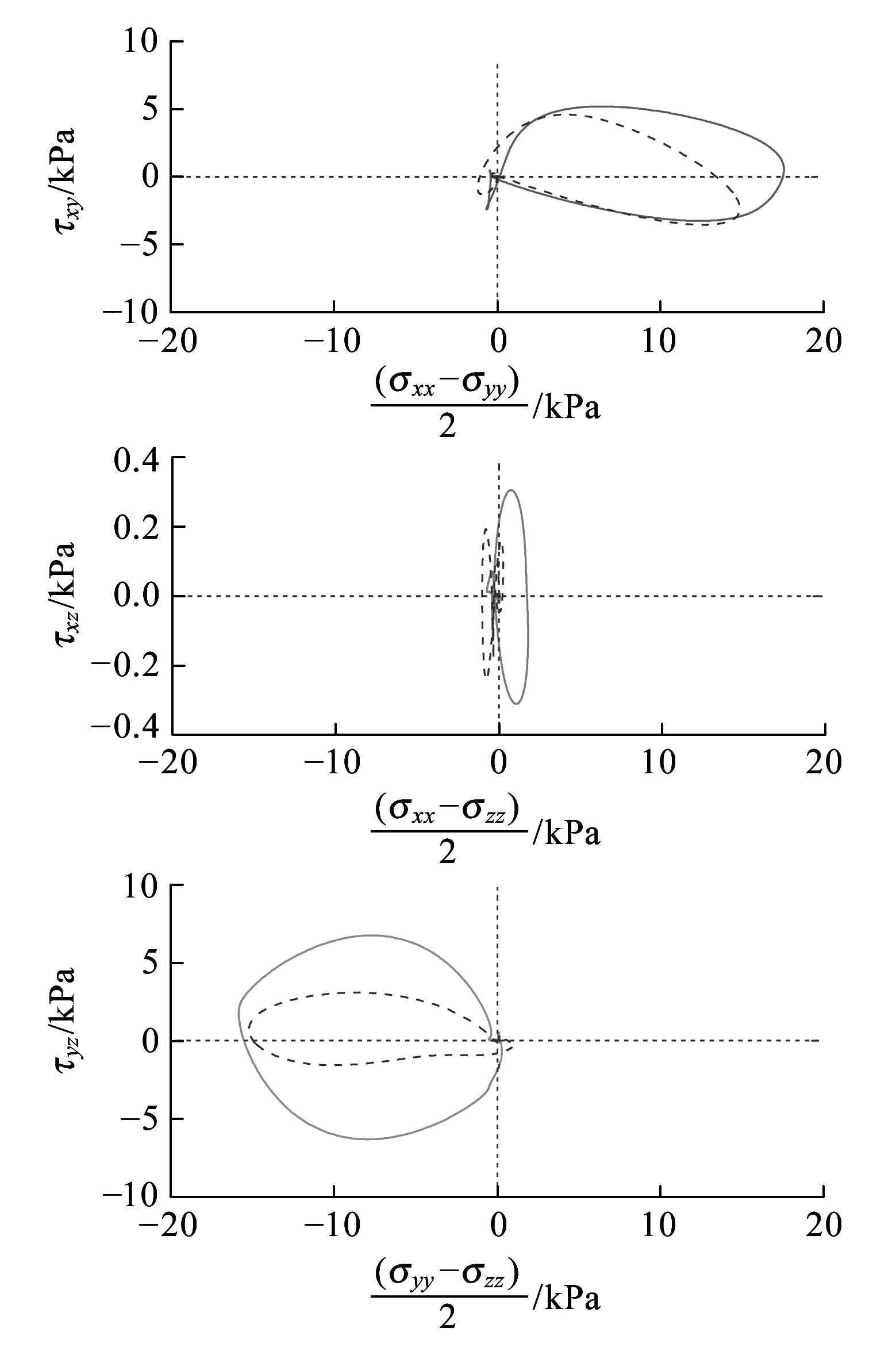
(a)0.5 m深度处单元1的应力主轴旋转

(b)5.0 m深度处单元2的应力主轴旋转

图7 土单元的应力主轴旋转

荷载的移动在地基中引发P波和S波两种应力波，这两种波的相互作用在地表附近生成Rayleigh波，它会干扰较浅地基土单元的应力状态，使这些位置单元的应力路径变得复杂。因此，图7中较浅处单元的应力主轴旋转没有明显的规律性，随着深度的增加，Rayleigh波的影响减弱，yz平面内的应力主轴旋转效应表现出明显的规律性，但不论单元处于哪一深度，xy、xz平面均无良好的规律性。

需要指出的是，单元2在yz平面内的应力主轴旋转并不完全关于横轴对称，特别是在原点附近，应力路径比较复杂，这是因为当荷载离开单元后，单元的动应力并不立即衰减为零而是要经历一个过程，这种滞后效应是采用静力学方法所不能求解的，因为(准)静态方法无法考虑移动荷载的动力效应，也无法反映地基土的真三维波动过程。

4 路基与地基中应力主轴旋转的异同分析

由以上分析可知，地基和高速铁路路基中的应力主轴旋转具有共性，即在xy、xz、yz三个平面内同步连续地旋转。地基中与路基受载钢轨正下方单元的应力主轴旋转以yz平面为主，非受载钢轨正下方单元的应力主轴旋转模式及强度与其存在明显差异。与地基相比，高速铁路路基中的旋转要复杂得多，还需进行深入探索。路基结构在横向不能视为弹性半无限空间体，其内部的静应力场分布不再具有均匀性。路基中还存在复杂的接触关系、大量的临空面和不同材料的交界面，应力波在这些界面处必将发生反射、折射和透射等现象，加上应力波由32个荷载激发，后续荷载对前面荷载的作用效应有增强作用，所以，路基中的应力波波场较复杂，目前还无法准确跟踪其传递过程。

从某种意义上来说，应力主轴旋转相当于一定程度的剪切作用，使得材料中的微小颗粒出现旋转、滑移和破碎，以至于引起材料较小的塑性累积变形。对高速铁路路基中任意一个土单元而言，列车每个轮对的作用都相当于一次冲击，应力主轴发生180°旋转。繁忙干线上的高速铁路路基，在服役期间承受的列车冲击可高达几千万甚至上亿次，由应力主轴旋转引起的塑性累积变形可达毫米量级。实际高速铁路路基的服役环境伴随着温度、湿度的交替变化，与超长周期、低应力水平、微振幅和低频率循环加载相互耦合，由此导致的路基塑性累积变形将会明显增大，这必然引起轨道系统的下沉，造成轨道几何不平顺，给列车的安全、稳定运行带来不利影响。

应力主轴旋转会引起材料的变形，已有的砂土试验研究表明，应力主轴旋转引起的体应变与主应力大小引起的体应变处在同一个数量级，在变形计算中是不容忽视的[15-16]。文献[17]的进一步研究发现，在工程中若不考虑实际发生的应力主轴旋转将导致偏于危险的设计。因此，在高速铁路路基累积变形计算中，不考虑应力主轴旋转效应将可能导致错误的结果。

5 结论

采用多尺度和精细化建模技术构建真三维条件下轨道-路基-地基非线性耦合动力分析模型，借助移动荷载模拟技术、动接触模拟技术和大规模并行计算技术，研究移动荷载作用下高速铁路路基中应力主轴的空间旋转效应及其规律，并与地基表面直接作用移动荷载引起的地基土应力主轴旋转进行了比较分析，得到如下结论：

(1)在地基表面直接作用移动荷载条件下，xy、xz平面内的应力路径无明显的规律。yz平面内，地基表层单元的应力路径受表面波影响大、规律性不强，较深处单元的应力路径具有明显的规律性。当荷载移动速度接近地基土表面波速时，地基处于一定程度的共振状态，土单元的应力路径比荷载移动速度大于地基土表面波速时的情况变化更大。

(2)移动荷载作用过程中钢轨正下方单元的应力主轴均发生同步、连续的旋转，受载钢轨正下方主要以yz平面内的旋转为主，非受载钢轨正下方主要以xy平面内的旋转为主。

(3)受载与非受载钢轨正下方相同深度单元的应力主轴旋转模式、强弱存在明显差异，高速铁路路基中的应力主轴旋转比地基中复杂，有待进一步研究。

参考文献：

[1]国家铁路局.TB 10621—2014 高速铁路设计规范[S].北京:中国铁道出版社,2015.

[2]赵学思.高速铁路路基体计算中的列车荷载模拟问题研究[J].铁道勘察,2007(3):55-56.

ZHAO Xuesi.Study on Simulate Issues of Trainload in Calculation of High Speed Railway Subgrade[J].Railway Investigation and Surveying,2007(3):55-56.

[3]KENJI I,IKUO T.Sand Response to Cyclic Rotation of Principal Stress Directions as Induced by Wave Loads[J].Soils and Foundations,1983,23(4):11-26.

[4]KENJI I.Soil Behaviour in Earthquake Geotechnics[M].Oxford:Clarendon Press,1995.

[5]王栋.波浪作用下海床动力响应与液化的数值分析[D].大连:大连理工大学,2002.

[6]胡一峰,李怒放.高速铁路无砟轨道路基设计原理[M].北京:中国铁道出版社,2010.

[7]王常晶.列车移动荷载作用下地基的动应力及饱和软粘土特性研究[D].杭州:浙江大学,2006.

[8]王常晶,陈云敏.移动荷载引起的地基应力状态变化及主应力轴旋转[J].岩石力学与工程学报,2007,26(8):1698-1704.

WANG Changjing,CHEN Yunmin.Stress State Variation and Principal Stress Axes Rotation of Ground Induced by Moving Loads[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(8):1698-1704.

[9]王常晶,温日琨,陈云敏.交通荷载引起的主应力轴旋转室内试验模拟探讨[J].岩土力学,2008,29(12):3412-3416.

WANG Changjing,WEN Rikun,CHEN Yunmin.Discussion on Laboratory Test Simulation of Principal Stress Axes Rotation Induced by Traffic Loading[J].Rock and Soil Mechanics,2008,29(12):3412-3416.

[10]王常晶,陈云敏.列车移动荷载在地基中引起的主应力轴旋转[J].浙江大学学报:工学版,2010,44(5):950-954.

WANG Changjing,CHEN Yunmin.Principal Stress Axes Rotation in Ground Induced by Train Moving Load[J].Journal of Zhejiang University:Engineering Science,2010,44(5):950-954.

[11]边学成,胡婷,陈云敏.列车交通荷载作用下地基土单元体的应力路径[J].土木工程学报,2008,41(11):86-92.

BIAN Xuecheng,HU Ting,CHEN Yunmin.Stress Path in Soil Element of Ground under Moving Traffic Loads[J].China Civil Engineering Journal,2008,41(11):86-92.

[12]汤连生,林沛元,吴科,等.单点动载下路基动应力状态及有效作用半径分析[J].岩石力学与工程学报,2011,30(S2):4056-4063.

TANG Liansheng,LIN Peiyuan,WU Ke,et al.Analysis of Dynamic Stress State and Effective Working Radius in Subgrade under Concentrated Load[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S2):4056-4063.

[13]丁智,葛国宝,魏新江,等.地铁列车运营引起的地基土应力状态变化分析[J].岩土工程学报,2013,35(S2):647-651.

DING Zhi,GE Guobao,WEI Xinjiang,et al.Variation of Stress State of Foundation Soils Induced by Running Subway[J].Chinese Journal of Geotechnical Engineering,2013,35(S2):647-651.

[14]薛富春,张建民.移动荷载作用下高速铁路轨道-路基-地基耦合系统振动加速度的空间分布特征[J].岩土工程学报,2014,36(12):2179-2187.

XUE Fuchun,ZHANG Jianmin.Spatial Distribution of Vibration Accelerations in Coupled Rail-embankment-foundation System on High-speed Railway under Moving Loads[J].Chinese Journal of Geotechnical Engineering,2014,36(12):2179-2187.

[15]于艺林,王富强,张建民.球应力循环加载下粒状土变形规律与本构描述[J].清华大学学报:自然科学版,2010,50(9):1365-1368.

YU Yilin,WANG Fuqiang,ZHANG Jianmin.Deformation Characteristics and Constitutive Modeling of Granular Soils during Cyclic Loading with Spherical Stresses[J].Journal of Tsinghua University:Science and Technology,2010,50(9):1365-1368.

[16]童朝霞,张建民,张嘎.考虑应力主轴循环旋转效应的砂土弹塑性本构模型[J].岩石力学与工程学报,2009,28(9):1918-1927.

TONG Zhaoxia,ZHANG Jianmin,ZHANG Ga.An Elastoplastic Constitutive Model of Sands Considering Cyclic Rotation of Principal Stress Axes[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(9):1918-1927.

[17]童朝霞,张建民,张嘎.应力主轴旋转对波浪作用下堤防变形的影响分析[J].工程力学,2009,26(10):67-73.

TONG Zhaoxia,ZHANG Jianmin,ZHANG Ga.Effects of Principal-stress-axis Rotation on the Deformation of a Dam under Wave Loading[J].Engineering Mechanics,2009,26(10):67-73.