高速铁路列车ATP安全制动曲线优化设计
李竹君,毛保华,苏 梅,柏 赟,陈 垚
(1.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044;2.中铁第四勘察设计院集团有限公司 技术中心,湖北 武汉 430063)
ATP系统是保证高速列车安全高效运行的系统,ATP安全制动曲线设计是车载ATP系统的关键技术之一。ATP安全制动曲线可根据列车制动性能和前方线路条件计算得到。通过安全制动曲线,ATP系统能实时对列车进行监控,若列车超速ATP系统将自动输出制动,以保证列车安全运行。
国内外学者针对列车制动控车模式和ATP安全制动曲线计算进行了深入研究。文献[1]研究高速铁路列车的制动减速度控制模式。文献[2]研究列车ATP系统的平行控制机理。文献[3]考虑列车制动过程中的滑行状态,构建ATP安全制动和触发曲线计算模型。文献[4]研究高速列车制动模式曲线的分段迭代模型。文献[5-6]研究变步长迭代方法计算ATP安全制动曲线,其基本计算原理为从防护目标点开始,按步长逆推计算ATP安全制动曲线。文献[7-8]针对城市轨道交通的列控系统和ATP系统超速防护功能进行了研究。既有研究为精准刻画高速铁路列车制动过程和准确计算ATP安全制动曲线提供了方法和借鉴。
由于车载计算机的容量和计算速度有限,上述理论计算方法较难应用于车载设备的实时计算。为了提升计算效率,ATP设备厂家一般采用简化算法。根据文献[9-10],目前我国高速铁路ATP车载设备供应商主要采用欧标法和日立法两种简化算法。欧标法将制动过程中列车自身产生的减速度(包括列车制动力和基本阻力产生的减速度,下文简称列车减速度)划分为最多6个阶梯,每个速度阶梯内取一个固定减速度值,再结合线路坡道近似计算[11]。
欧标法基本按照减速度的固定间隔划分速度阶梯,阶梯内取平均减速度。这种简化能够满足车载设备实时计算需求,但与理论计算曲线相比,曲线整体效率偏低且存在一定安全隐患。文献[12]提出以速度阶梯内最小减速度替代平均减速度,并按欧标法曲线制动距离与理论制动距离的平方差之和最小的原则进行速度阶梯的选择,为优化设计速度阶梯分界值提供了思路。该方法保证了行车安全,但减速度取值更为保守,易产生效率较低的曲线。并且,在制动过程中,若列车安全余量波动较大,不利于行车安全和司机平稳操纵。随着高铁客运需求的日益增长,如何优化设计欧标法的速度阶梯分界值,在保证行车安全前提下尽量提升ATP安全制动曲线效率,对进一步提升铁路通过能力具有重要意义。
本文基于欧标法计算原理,构建欧标法逆推计算模型,并在此基础上,以ATP安全制动曲线效率损失最低和安全余量波动性最小为目标,构建速度阶梯分界值优化模型,并设计算法求解。探讨在不同车载计算速度限制条件下的分界值选择方案,并分析不同线路条件和列车制动性能下的一般设置规律。
1 欧标法计算模型
在制动过程中列车主要受力为制动力、基本阻力以及线路附加阻力。这里设列车制动减速度为b,列车单位基本阻力为w0,坡道附加阻力为wi,曲线附加阻力为wr,e为列车回转质量系数。
列车运动过程中,合力随速度的变化而变化,不是恒定值。理论法[3]将制动过程细分成M(0)个速度步长Δv(0),假设在该步长内列车合力减速度不变,结合运动学方程计算速度步长Δv(0)内的距离增量ΔS(0),并按步长从防护目标点进行逆推计算,如图1所示。
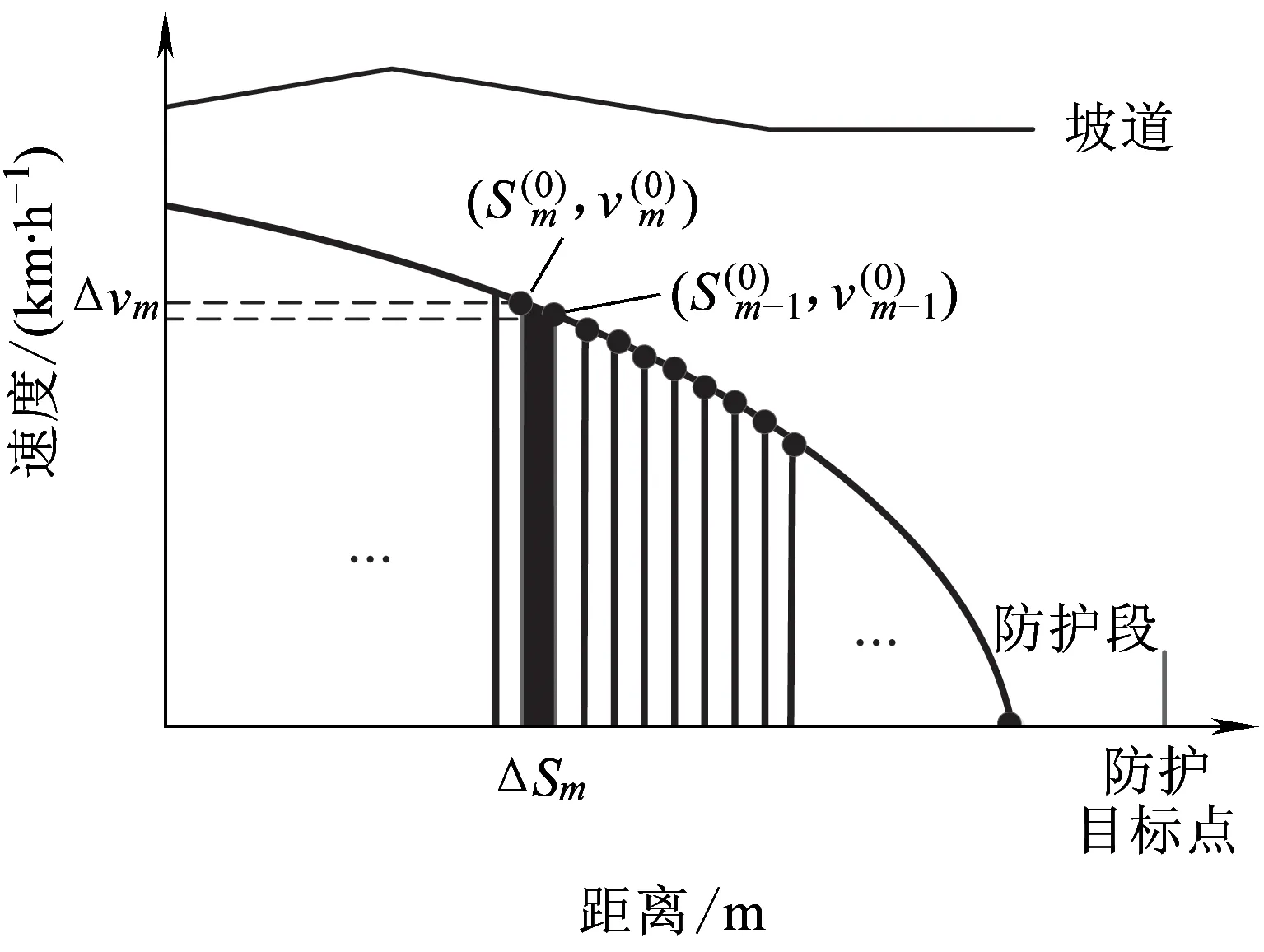
图1 理论法按步长逆推计算
理论法中每个速度步长需重新计算列车合力减速度,计算过程较为复杂。而欧标法仅考虑列车减速度与坡道阻力减速度,且同一速度阶梯内的列车减速度和同一坡道内的坡道阻力减速度保持不变,因而列车合力减速度仅在变坡点和速度阶梯分界值发生改变。根据列车合力减速度的变化点,可将制动过程划分成M个阶段,每个制动阶段内合力减速度不变。从防护目标点,逆推计算每个制动阶段m的速度增量Δv和位移增量ΔS。
假设从防护目标点逆推,第j个坡道坡度为wi(j),变坡点为Lj(j=1,2,…,J),如图2所示。将制动过程划分成K个速度阶梯,每个速度阶梯分界值为Vk(k=1,2,…,K,V0=0 km/h,VK=350 km/h),投影到位移方向为分界点Sk,第k个速度阶梯(Vk-1,Vk]内对应的列车减速度为ak。为确保行车安全,本文取该速度区间列车减速度的最小值,即

图2 欧标法按制动阶段逆推计算
( 1 )
式中:b(v)为列车制动减速度;w0(v)为列车基本阻力。
如图2所示,曲线上第m个制动阶段的分界点(Sm,vm)可由(Sm-1,vm-1)逆推计算为
Sm=min(Sp,Lq)
( 2 )
( 3 )
式( 2 )表示第m个制动阶段分界点Sm为下一个离分界点Sm-1最近的合力减速度变化点,式( 3 )同理。式( 2 )中Sp为速度阶梯分界值在位移方向的投影,式( 3 )中cm为第m个制动阶段的合力减速度。
( 4 )
cm=ap+0.009 8wi(q)
( 5 )
p=min(k|Vk>vm-1)k∈[1,K]
( 6 )
q=min(j|Lj>sm-1)j∈[1,J-1]
( 7 )

( 8 )
( 9 )
2 优化模型
文献[12]指出,速度阶梯内减速度应取最小值,若取平均值或其他值则有可能出现计算制动距离小于实际制动距离的情况。为了确保行车安全,本文将速度阶梯内的减速度取为该速度区间的最小减速度。这样造成两个方面问题:一,减速度保守取值损失了曲线效率,影响铁路的运输效率和通过能力;二,速度阶梯内恒定的减速度取值,造成了安全余量的不均匀分布。
由于欧标法中列车减速度取值保守,因而相比于理论法,曲线从制动起点至防护目标点之间的制动时间将增多。这里将增加的制动时间所占比例定义为曲线效率损失U。
(10)
式中:T(0)和T分别为理论法曲线和欧标法曲线的制动时间。当列车制动性能和线路条件一定时,理论曲线制动时间为定值,且恒小于欧标法曲线制动时间。因而,效率损失U越小表明欧标法曲线制动时间越少,则对应的速度阶梯分界值方案越优。

(11)
安全余量波动性越小表示两种曲线的相对差异水平较为稳定,说明欧标法曲线设计的安全可靠性较高,则对应的速度阶梯分界值方案越优。
这里用制动过程中各初速度下安全余量的标准差来表示安全余量的波动性,并以安全余量标准差最小和曲线效率损失最低为两个优化目标,构建欧标法速度阶梯分界值优化模型。
y1=minU
(12)
(13)
s.t.
Vk>Vk-1,Vk∈[0,350],Vk∈Z
(14)
式( 1 )~式(11)
3 算法
本文提出的优化模型是一个非线性整数规划问题,较难通过解析法或Cplex等软件求解最优解。遗传算法(GA)具有快速搜索全局最优解的能力,能处理复杂非线性系统优化问题。本文采用GA求解,基本步骤如下:
步骤1染色体编码。模型需要优化的参数为速度阶梯分界值Vk。由于速度分界值Vk需要从小到大排列,若将Vk按次序进行0-1编码,则在染色体交叉和变异操作中易产生大量不可行解,影响最优解的进化效率。Vk取值范围为速度区间(Vk-1,VK),可由式(15)将其线性变换至区间(0,1)。
(15)

步骤2初始种群生成。设种群规模为O,随机产生pop_size组K-1个(0,350)之间互不相等的正整数。
步骤3计算种群适应度函数。本文构建的优化模型为最小化问题,每次迭代过程中,根据式(12)和式(13)计算得到模型的目标值y1、y2后,通过计算求得每个染色体的适应度。
f1=1/y1
(16)
f2=1/y2
(17)
(18)
式(16)和式(17)将模型转变为最大化问题,式(18)将双目标进行归一化处理从而计算得到种群适应度,λ1和λ2为两个目标的权重系数。
步骤4更新种群。种群的更新操作包括选择、交叉与变异操作。
步骤5判断终止条件。判断迭代次数是否达到最大迭代次数要求,若是则输出计算结果;否则,返回步骤三。
本文采用遗传算法求解,在主频2.8 GHz,运行内存4 G电脑上,求解时间约为5 h。由于欧标法速度阶梯分界值的选择是离线问题,遗传算法的求解时间可满足要求。
4 案例分析
本文选取CRH380A-2808动车组,以岳阳东站下行方向列车进站减速区ATP常用制动曲线为例,验证模型和算法有效性。
4.1 模型效果验证


图3 曲线效率优化前后对比

图4 曲线制动过程安全余量波动情况
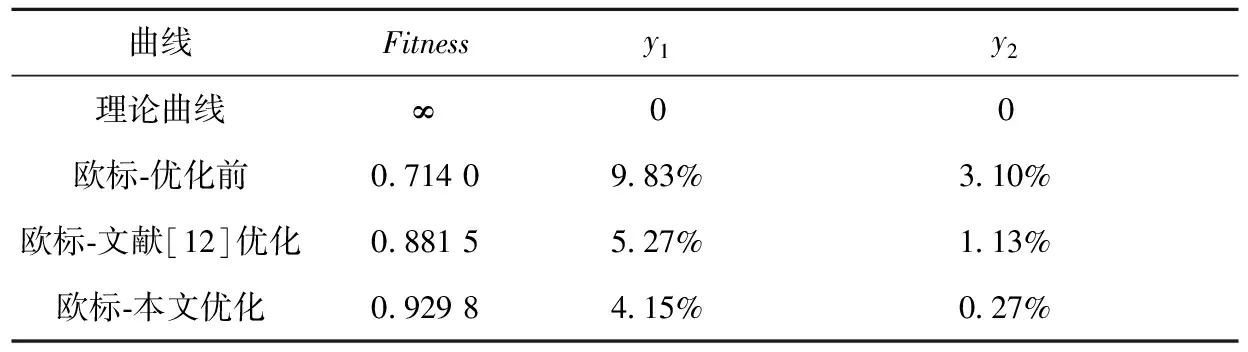
曲线Fitnessy1y2理论曲线∞00欧标⁃优化前0 71409 83%3 10%欧标⁃文献[12]优化0 88155 27%1 13%欧标⁃本文优化0 92984 15%0 27%
基于遗传算法,优化后的速度阶梯分界值方案为(17,99,158,222,279)。表1和图4表明,相比于优化前,文献[12] 优化后曲线的安全余量波动较小,效率损失达到5.27%;本文优化后曲线在效率和安全余量方面有较好的表现。结合图3可以看出,这是因为本文优化后曲线在速度低于171 km/h区间内效率损失高于优化前,而在速度高于171 km/h区间内则低于优化前。这样既从整体上使得安全余量分布更加均匀,又降低了效率损失,有利于同时提升效率和行车安全可靠性。
4.2 参数分析
上述优化设计模型中,车载设备的计算速度限制、线路条件和列车制动性能,是影响速度分界值设置的三个关键参数。本文探讨上述三个参数变化下的速度阶梯分界值设置规律。
(1) 车载设备计算速度
欧标法速度阶梯数量K越大,曲线计算时间越长,对车载设备计算速度要求越高。这里对速度阶梯数量K进行灵敏度分析,给出不同K值情况下的速度阶梯分界值方案(表2),以适应不同的车载设备计算能力。在主频2.8 G,运行内存4 G的计算机上进行ATP安全制动曲线计算速率的测试,制动初速度v=350km/h。
表2中,随着速度阶梯数量增加,计算时间的增长速率越来越快,而车载设备计算速度约为140 M/s。这验证了速度阶梯不宜过多,最多选择6段的合理性。当阶梯数小于3时,效率损失高达17.6%。这说明,有必要根据车载设备计算速度合理设置速度阶梯数量,以求在计算效率和曲线效率两方面达到更高水平的统一。

表2 不同速度阶梯数量K下的速度阶梯分界值方案
(2) 线路条件
将线路条件分别设置为-35‰、-20‰、-10‰、0‰、10‰、15‰、20‰坡道,探讨坡度变化时速度阶梯分界值的变化规律,见表3。
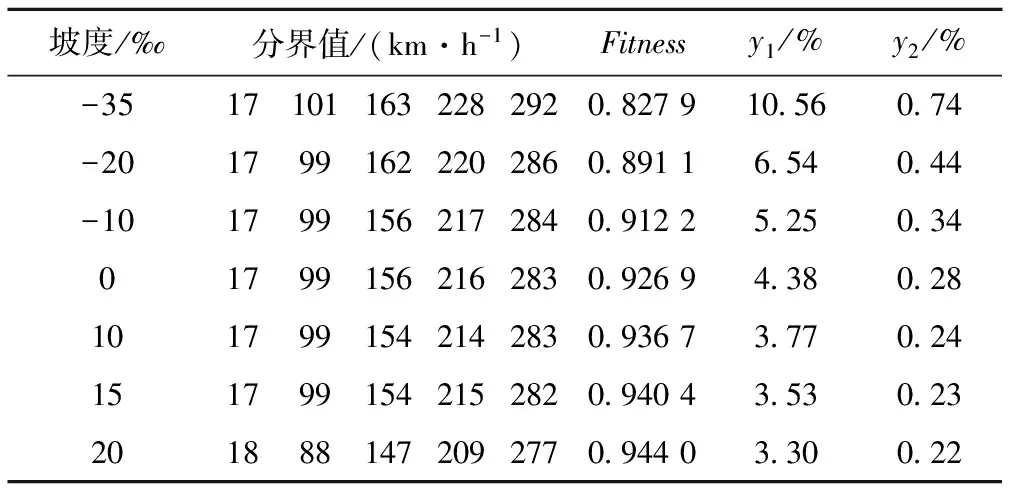
表3 不同线路条件下的速度阶梯分界值方案
表3中,当线路坡度在-20‰至15‰范围内波动时,速度阶梯分界值基本完全一致;当坡道为15‰至20‰的大上坡时,速度阶梯分界值减小5~10 km/h;当坡道为-20‰至-35‰的大下坡时,速度阶梯分界值增大6~8 km/h。这说明,优化后的速度阶梯分界值在一定坡度变化范围内效果是比较稳定的,但当坡度大于10‰或者小于-20‰时,速度阶梯分界值有必要进行重新优化设计。根据我国相关技术标准,线路平均坡度一般在±20‰之内,因而优化后的速度阶梯分界值方案具有较好的适用性和稳定性。
(3) 列车制动性能
不同型号列车制动性能有所差异,同一列车在运行过程中制动性能状况也有波动。下面将从上述两个方面,分析列车制动性能对速度阶梯分界值的影响。
这里选取CRH380A-2808号、CRH380A-6038号和设计车型CRH380A-5,比较分析三种车型优化后的速度阶梯分界值,如图5所示。

图5 不同制动性能下的速度阶梯分界值(V2,V4,V5)变化趋势
图5表明,中高速区列车制动性能越差,速度阶梯分界值则相对偏小,但V1基本不变。这说明,列车在中高速区制动性能较差,减速度曲线呈现两边低中间高的陡峭下降趋势,速度分界值向较小的方向取值。
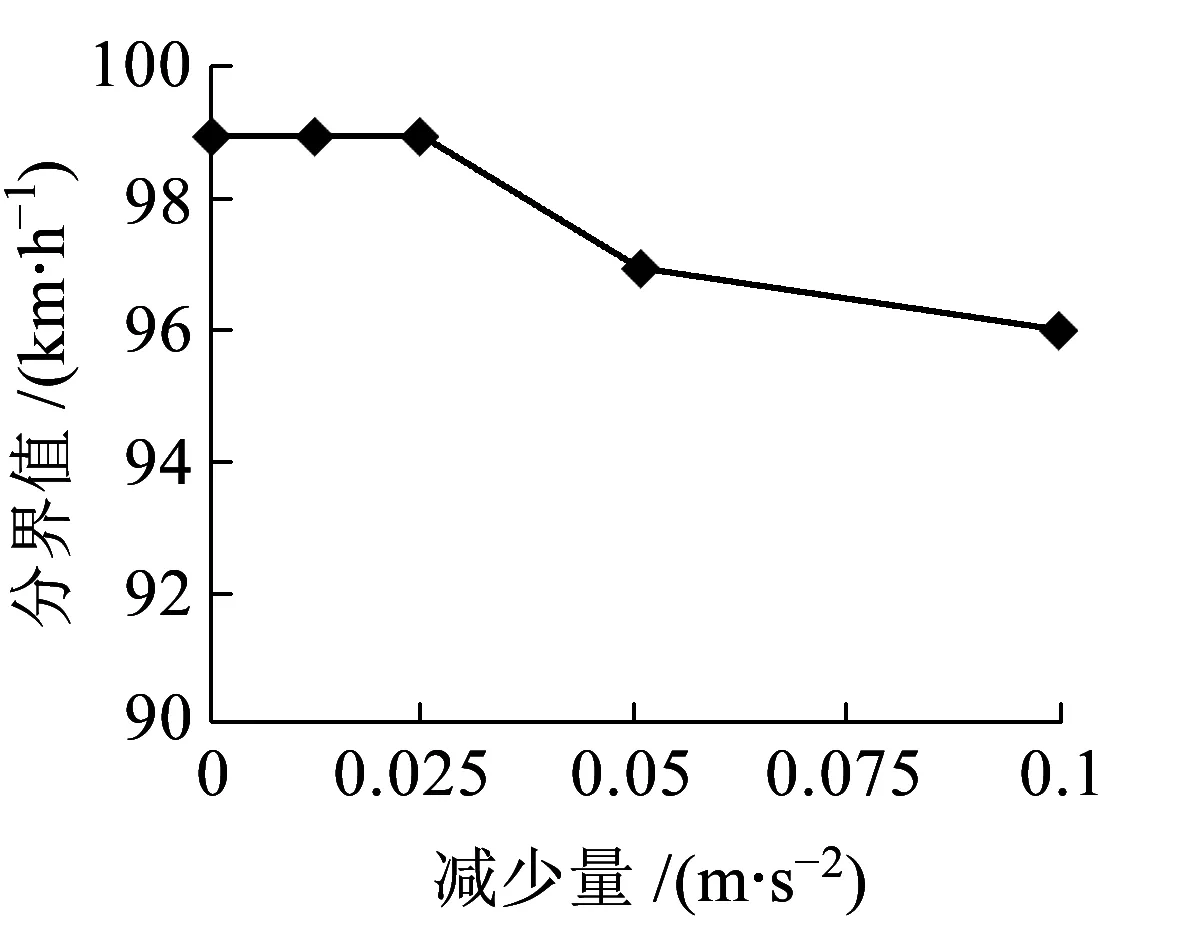
根据文献[13],列车运行过程中天气、轨道状况等变化,将导致列车车轮黏着状态发生变化,从而导致列车制动性能整体下降,影响制动减速度大小。这里以CRH380A-2038号动车组为基础车型,模拟黏着系数μ发生改变后的列车减速度曲线,分别将对应列车减速度的减少量Δt设为0.012 5、0.025、0.05、0.1m/s2,分析其对黏着状态变化的灵敏度。
(a)V2

(b)V4

(c)V5图6 黏着状态波动下的速度阶梯分界值(V2,V4,V5)变化趋势
图6展示了第2、4、5个速度阶梯分界值(V2,V4,V5)的变化趋势。结果表明,随着列车制动减速度降低,速度阶梯分界值整体呈变小趋势。当Δt≤0.025 m/s2,速度阶梯分界值基本不发生变化;当0.05 m/s2≤Δt<0.1 m/s2,速度阶梯分界值整体减小2~5 km/h。当Δt=0.1 m/s2时,若不重新优化速度阶梯分界值,曲线效率损失为4.81%,安全余量标准差为0.24%。说明黏着系数在一定范围内波动时,优化后的速度阶梯分界值稳定性较好;若制动减速度减少量大于0.1 m/s2,则可考虑重新优化速度阶梯分界值。
5 结论
本文优化设计欧标法速度阶梯分界值,并分析不同线路条件和列车制动性能情况下,速度阶梯分界值的设置规律。案例结果表明,优化后的欧标法曲线能够将效率损失由9.83%减少至4.27%,安全余量波动性由3.1%减少至0.27%。灵敏度分析结果表明,线路坡道、列车制动性能在一定范围内波动时,优化后的速度分界值稳定性较好。若超过一定范围时,为防止出现防护效果较差的曲线,需重新优化速度阶梯分界值。本文的设计方法比较关注曲线本身效率损失和安全余量分布,并未考虑列车操纵方案。如何结合实际列车运行行为来设计ATP安全制动曲线,仍有待进一步研究。
《南方日报》以及其所属的南方报业传媒集团的党性是不容置疑的,这从张军工作服上的党徽、优秀工作人员工位上摆放的“党群先锋岗”的标识等细节上,就可见一斑。因而,相较其他类型的印刷企业,南方印务拥有更强的政治责任。
参考文献:
[1]吴萌岭, 程光华, 王孝延, 等. 列车制动减速度控制问题的探讨[J]. 铁道学报, 2009, 31(1): 94-97.
WU Mengling, CHENG Guanghua , WANG Xiaoyan ,et al. Discussion of Braking Deceleration Control of Railway Vehicles[J]. Journal of the China Railway Society, 2009, 31(1): 94-97.
[2]WANG J, LI Y, ZHANG Y. Research on Parallel Control Mechanism and Its Implementation in ATP[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(6): 1652-1662.
[3]林颖, 王长林. 基于CBTC的车载ATP安全制动曲线计算模型研究[J]. 铁道学报, 2011, 33(8): 69-72.
LIN Ying, WANG Changlin. Computational Model of Safe Braking Curve of Onboard ATP Based on CBTC[J]. Journal of the China Railway Society, 2011, 33(8): 69-72.
[4]上官伟, 蔡伯根, 王晶晶, 等. 时速250km以上高速列车制动模式曲线算法[J]. 交通运输工程学报, 2011, 11(3): 41-46.
SHANGGUAN Wei, CAI Baigen, WANG Jingjing, et al. Braking Mode Curve Arithmetic of High-speed Train above 250 km·h-1[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 41-46.
[5]谭莉, 王长林. CTCS3级列控系统ATP防护曲线算法研究[J]. 铁路计算机应用, 2014, 23(7): 48-57.
[6]刘循. 基于变步长迭代逼近的轨道交通列车运行计算方法[J]. 中国铁道科学, 2013, 34(1): 82-87.
LIU Xun. Train Operation Calculation Method of Rail Transit Based on Variable Step-size Iterative Approximation[J]. China Railway Science, 2013, 34(1): 82-87.
[7]刘海东, 苏梅, 彭宏勤. 城市轨道交通列车制动问题研究[J]. 交通运输系统工程与信息, 2011, 11(6): 93-97.
LIU Haidong, SU Mei, PENG Hongqin. Braking Performances of Urban Rail Trains[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(6): 93-97.
[8]宋芹, 陈凯, 崔淑妮, 等. 城市轨道交通国产ATP车载设备超速防护功能的仿真实现[J]. 中国铁道科学, 2011, 32(2): 48-52.
SONG Qin, CHEN Kai, CUI Shuni, et al. Simulation of Overspeed Protection of Onboard ATP Device in UMT[J]. China Railway Science, 2011, 32(2): 48-52.
[9]卫和君. 高铁车载ATP制动控车模式曲线计算方法的研究[J]. 铁路通信信号工程技术, 2013(S): 33-38.
WEI Hejun. Calculation Method of ATP Curve Onboard System for High-speed Rail Railway[J]. Signalling & Communication Engineering, 2013(S): 33-38.
[10]Rail Transit Vehicle Interface Standards Committee of the IEEE Vehicular Technology Society. IEEE Standard for Communications-based Train Control (CBTC) Performance and Functional Requirements[S]. The United States of America : the Institute of Electrical and Electronics Engineers, 2005: 18-19.
[11]UIC Code 544-1[S]. The European Union: Union International Des Chemins De Fer, 2004.
[12]黄卫中, 季学胜, 刘岭, 等. CTCS-3级列控车载设备高速适应性关键技术[J]. 中国铁道科学, 2010, 31(3): 87-92.
HUANG Weizhong, JI Xuesheng, LIU Ling, et al. Several Crucial Techniques for the High-speed Adaptability of CTCS-3 Train Control Onboard Equipment[J]. China Railway Science, 2010, 31(3): 87-92.
[13]毛保华. 列车运行计算与设计[M]. 北京: 人民交通出版社, 2008: 75-76.

