基于FPGA的相关法测量相位差

唐升，王天翔，雷浩丹，侯榆青，吕亚林

（1.西北大学 信息科学与技术学院，西安 710127；2.济南市计量检定测试院，济南 250002）

0 引言

准确测量两个弦波信号之间的相位差在通信、电力、地质勘探、故障诊断、航空航天等领域有着重要意义[1-4]。近年来，随着电子计算机技术的不断发展和相位差测量在不同应用领域技术需求的不断增加，涌现出许多的相位差测量方法。根据不同的电路类型和结构，这些测量方法可以分为传统模拟方法和数字方法。得益于微处理器与大规模集成电路的发展，数字化的测量方法表现出诸多优点。例如，精度高、体积小、成本低、灵活性好等[5-8]。数字化测量方法的实现大多依赖于计算机、微处理器（MCU，microcontroller unit）或数字信号处理器（DSP，digital signal processor）平台。目前拥有多核处理器的计算机平台在实现大数据量算法的时候通常不会存在运算速度不足的问题，但是很难满足测量系统的便携性、小型化需求。体积相对较小的测量系统一般采用MCU或DSP来实现数据运算处理，它们的算法指令通常在芯片内部被顺序地执行，随之而来的速度瓶颈是不可避免的。现代高速和大容量现场可编程门阵列FPGA（field programmable gate array）的出现和应用有望克服上述技术方案的缺点。本文提出了一种基于FPGA的数字相关法测量弦波信号相位差的技术方案，并针对技术方案中数据同步采集问题和利用硬件描述语言（Verilog HDL或Verilog）实现相关法的关键技术进行了讨论分析，并给出了解决方案。

1 相关法测量弦波信号相位差的基本原理

与传统的计数器测量不同，相关法测量相位差是一种以数字信号处理为核心的数字化测量技术。概括而言，该方法使用若干针对两个待测弦波信号的采样点来计算它们的互相关函数值和自相关函数值，并通过反余弦求解来完成两个信号相位差的解算。

假设两个待测弦波信号为正弦信号，分别表示为：

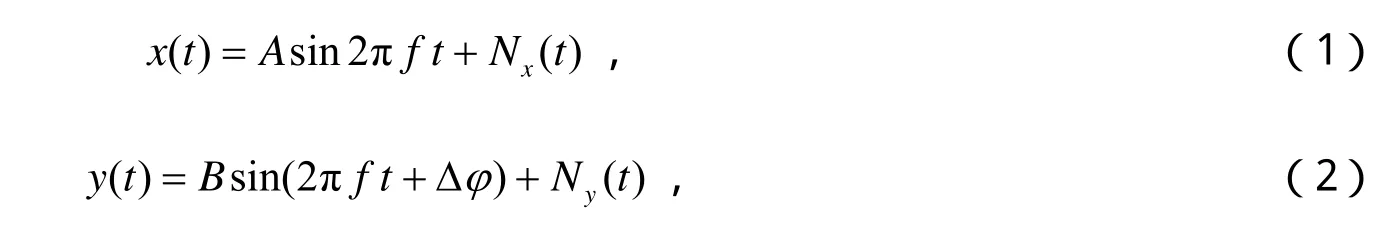
式（1）和（2）中，A和B分别表示两个待测信号的幅度值。其中的分别表示叠加在两个信号上的噪声。jD是两个待测信号之间存在的相位差值。

针对两个待测弦波信号(x)t和(y)t在时间T内进行相关处理，有：

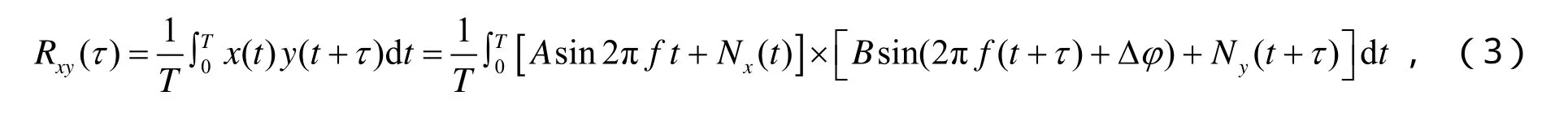
式（3）中，T的取值一般为待测信号周期的整数倍。而且从式（3）可以看出，两个待测弦波信号(x)t和(y)t的互相关函数值的大小主要取决于两个信号之间的相位差jD和延迟量t的大小。当t→0的时候，互相关函数值的大小就主要由两个信号之间的相位差Dj决定。通常情况下，弦波信号和随机噪声不相关，而且两个随机噪声之间也可认为不相关。如果0t=，那么式（3）将简化为：

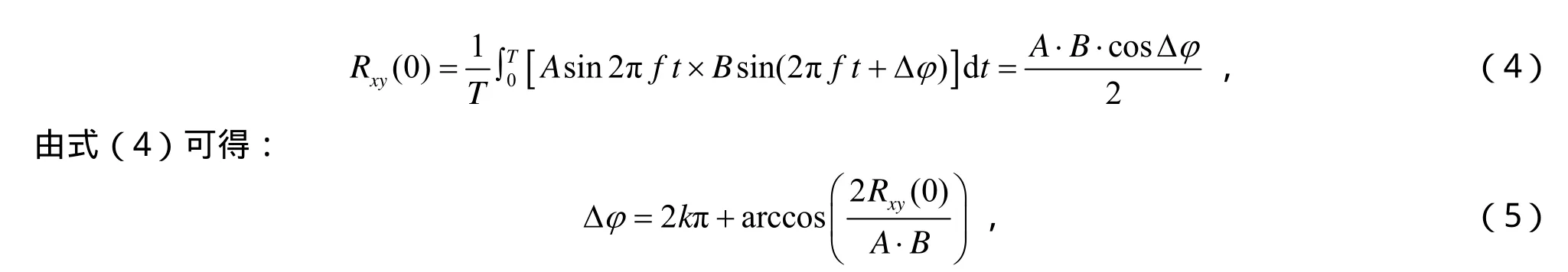
式（5）中，k＝0，1，2，…。在两个待测弦波信号(x)t和(y)t的相位差不大的情况下，k＝0。又因为两个待测弦波信号(x)t和(y)t的幅度值与其自相关函数之间存在如下关系：

由式（8）可见，通过计算两个弦波信号的互相关函数值和自相关函数值，并通过反余弦求解即可实现两个信号相位差的解算。

2 相关法测量相位差的FPGA实现

利用MCU或DSP实现数字信号处理算法时，数据和指令必须在存储器和运算器之间传输才能完成运算，它们的运算任务被分解成一系列依次执行的“读取-运算-储存”过程，所以运算过程在本质上是串行的，使得计算速度受到存储器和运算器之间信息传输速度的限制。FPGA是一种新型的数字电路。传统的数字电路芯片都具有固定的电路和功能，而FPGA可以直接下载用户现场设计的数字电路。FPGA技术颠覆了数字电路传统的“设计-流片-封装”的工艺过程，直接在成品FPGA芯片上开发新的数字电路，扩大了专用数字电路的用户范围和应用领域。FPGA芯片中的每个逻辑门在每个时钟周期都同时进行着某种逻辑运算，因此FPGA本质上是一个超大规模的并行计算设备，非常适合用于开发并行高速计算应用。因此，本文以FPGA为运算核心，提出一种基于相关法的弦波信号相位差测量方案。设计方案的基本结构如图1所示，包括了信号调理电路、数据同步采集电路、FPGA电路和串口电平转换电路。

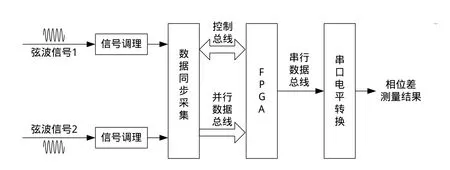
图1 系统结构

2.1 数据的同步采集

如图1所示的弦波信号相位差测量中，两个待测信号首先经过信号调理，然后进行数据的同步采集和处理。信号调理的作用是将待测信号进行适当转换，使之满足后级电路的输入要求。数据同步采集电路的主要功能是将信号调理后的两个弦波信号进行采样，并将采样数据通过数据总线传送至FPGA进行数字信号处理，解算相位差。这种数字化测量模式要求对两路弦波信号的每一次采样严格在同一时刻完成。如图2所示，其中TD为数据采样间隔，Au为信号幅度，t为采样时间。假设针对两个弦波信号的采样不在同一时刻，而是两次采样之间存在一个微小的时间差tD，那么计算两个信号相位差jD时有：

式（9）中，rjD为两个待测弦波信号之间的实际相位差，f为它们的频率标称值，2πftD为非同步采样导致的测量误差。

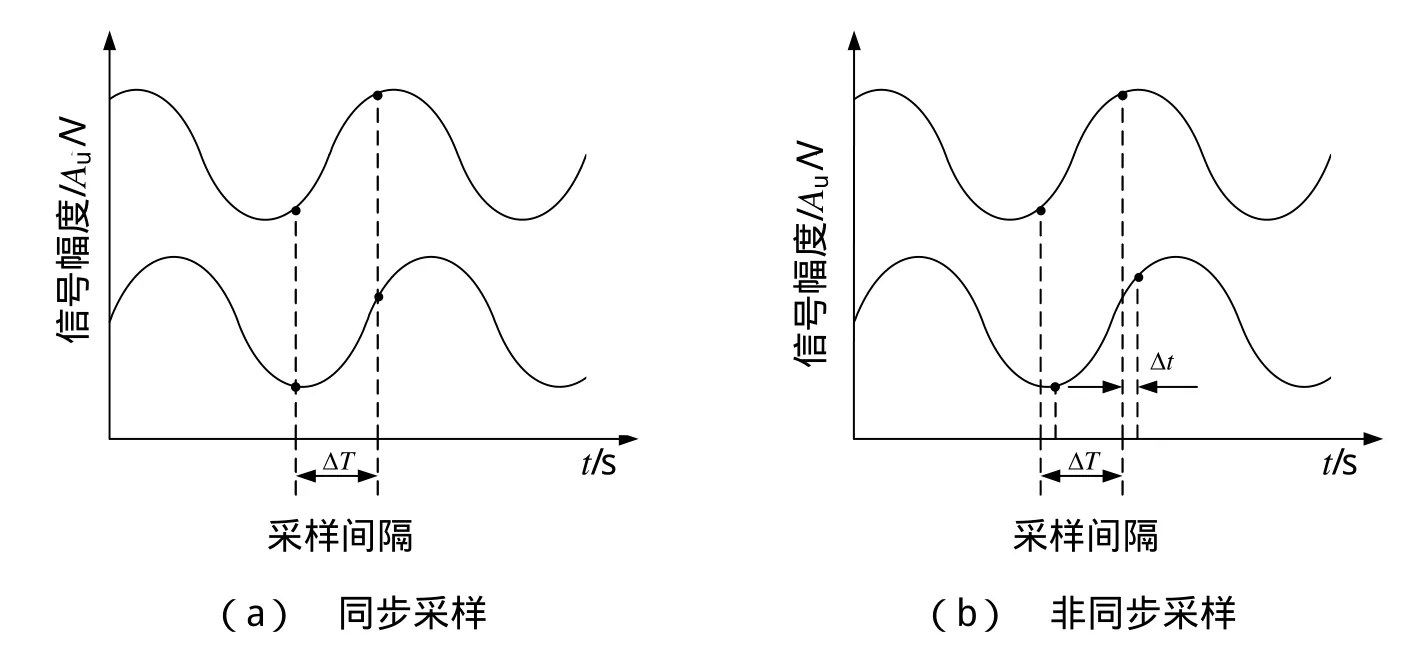
图2 针对弦波信号的同步采样与非同步采样

因此电路设计中应选择合理的AD转换器，并严格控制对应两个AD转换器的采样时序，以避免或尽量减小上述非同步采样误差。本文所提出的设计方案中使用16位AD芯片ADS8364实现同步采样。如图3所示，系统设计前端的信号调理电路基于TI公司的运算放大器芯片OPA4132设计，主要作用是对输入的弦波信号进行等比例电平转换，使之输出的两路差分信号符合ADS8364的输入电压范围。两路差分信号经由两组匹配电阻输出至ADS8364的CHA0采样通道和CHA1采样通道。ADS8364的采样参考电压REFin由芯片内部参考电压REFout提供；同时REFout电压经过电容稳压滤波后输出至信号调理电路作为差分电压的参考。ADS8364的4条控制总线CLK，EOC，RD和HOLDA负责交互传递它与FPGA之间的逻辑控制指令，其中的HOLDA为采样控制信号。由于电路设计中一个HOLDA信号同时控制CHA0和CHA1两个采样通道，那么可以认为ADS8364的非同步采样误差主要由器件本身的孔径抖动决定。孔径抖动是AD转换器内部的采样保持开关延迟不确定性造成的采样信号相位误差[9-10]。查阅芯片制造商的官方数据手册可知ADS8364的孔径抖动典型值是50 ps[11]。例如，数字化测量100 Hz弦波信号之间的相位差，由ADS8364的孔径抖动导致的相位误差约为1.8×10-6°，可以忽略不计。

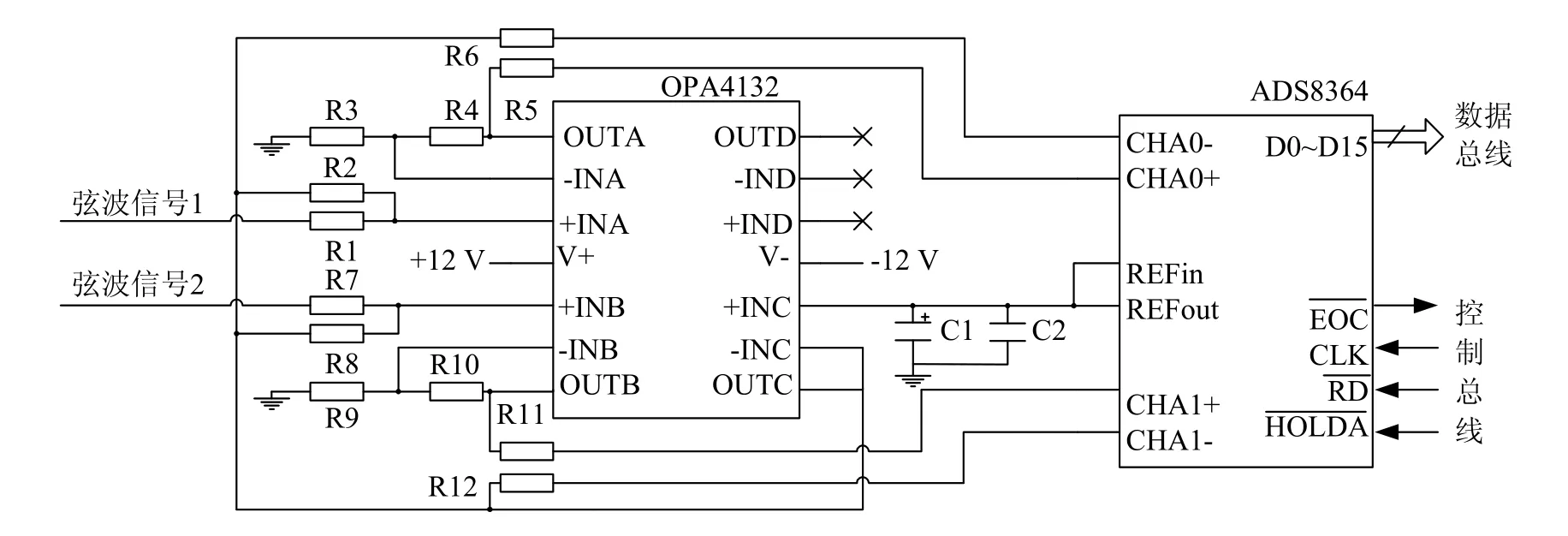
图3 数据同步采集电路

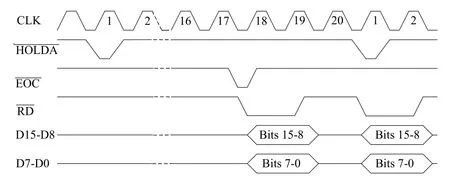
图4 数据同步采集电路的时序逻辑

2.2 基于硬件描述语言的测量算法实现

虽然FPGA具有MCU和DSP不可比拟的高速并行处理优势，但是不可否认它在数值计算，尤其是有符号数的运算处理的灵活性表现稍逊。通常情况下，FPGA不能直接处理有符号数。因此在系统设计中，将两路待测弦波信号的采样数据同时叠加一个正向偏移量M。M的取值略大于待测信号的幅值，从而将整个相关法测量相位差的运算变为无符号运算，简化FPGA利用硬件描述语言（Verilog HDL或Verilog）实现相关运算的复杂度。因此，两路被测信号变为：

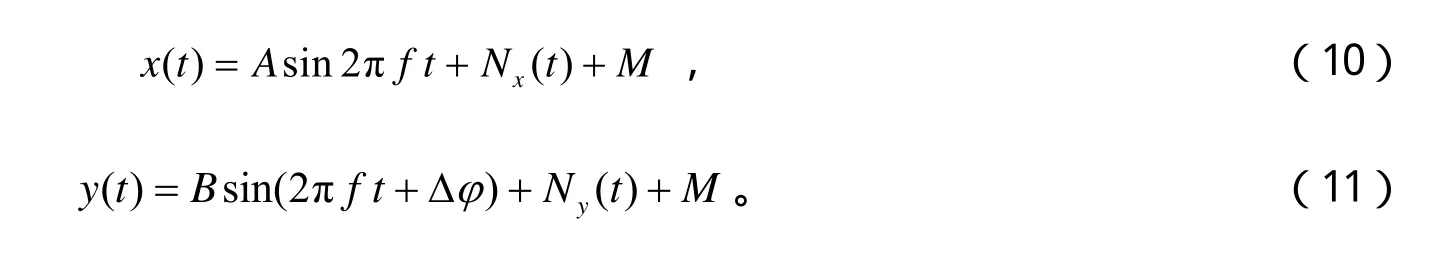
相应地，两待测弦波信号之间的自相关函数和互相关函数可表述为：

那么，两待测弦波信号相位差的测算式可表述为：

同时，因为三角函数存在如下关系：

所以，相位差测算式也可表述为：

由式（17）可知，在偏移量M已知的前提下，只要利用采样数据准确计算两待测弦波信号的自相关值和互相关值，再进行反正切运算，即可推算出它们之间的相位差。由图3可知，由OPA4132为核心构建的信号调理电路决定了本文测量方案的弦波信号电压为±2.5 V，那么本系统方案中M的取值设定为2.5，即可满足算法的无符号运算要求。

系统方案中的FPGA选用Altera公司的Cyclone EP1C12Q240I7N。FPGA的16条数据总线与同步采样芯片ADS8364的16条数据总线相连，它的串行数据输出DX_0连接至串行口驱动电路。同时，利用硬件描述语言在FPGA芯片内部构建功能电路，如图5所示，具体包括时序逻辑电路、数据预处理电路、相关器、加法器、根号器、反正切变换器等。其中反正切变换器设计实现相对复杂，是系统设计的核心。

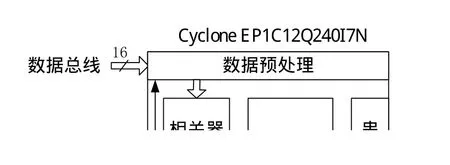
图5 硬件描述语言实现相关法测量相位差

本文反正切变换器设计中引入了坐标旋转计算机（CORDIC，coordinate rotation digital computer）算法[12]。CORDIC算法实现反正切计算的基本思想是用一系列与运算基数相关的角度不断逼近所需旋转的角度，其本质是一种数值逼近的方法，运算过程仅涉及到移位和加减法操作，因而适合FPGA的硬件描述语言实现[13-19]。

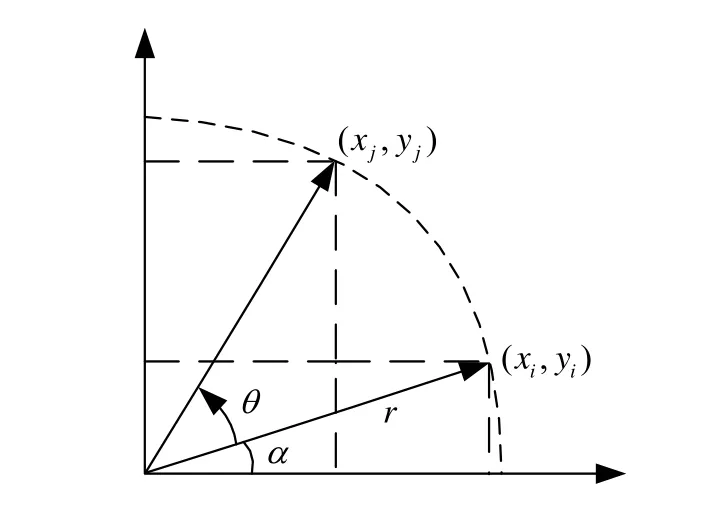
图6 向量旋转示意图

可以将式（18）改写为矩阵向量形式：

提出式（19）中的因数cosq，则变为：

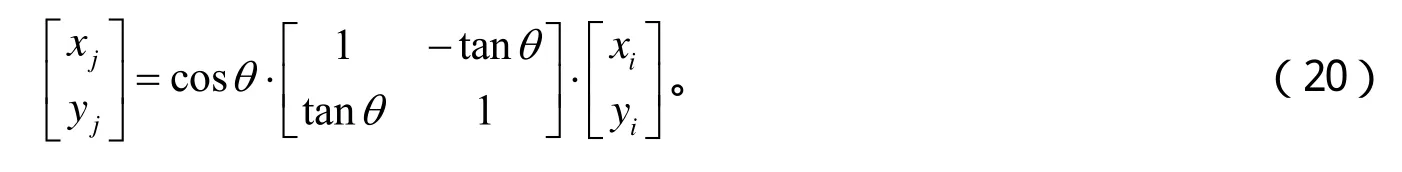
将式（20）中的cosq去除，可以得到：

式（21）是一个“伪旋转”方程式，即相对于式（20）所示的向量旋转而言，x，y的值增加至它们的倍，向量模值变大，但是其旋转的角度是相同的。任意角度q的向量旋转，可以通过一系列连续的小角度旋转迭代来完成。假设第n次旋转角度为nq，则有：

如果旋转过程遵循如下法则：

在式（24）的基础上再引入第3个方程（可称之为角度累加器），用来在每次迭代时追踪累加的旋转角度：

那么整理式（24）和（25）得到CORDIC算法实现反正切的3个基本迭代方程：

工笔花鸟细化的形式美很大程度上取决于在线条上的运用，整齐划一的线条需要扎实的功底，需要时间的打磨才能成就线条的力度美感，讲究在器物的身上线条需要一气呵成。

如果判决算子nd满足下列条件：

基于式（26）所示的基本迭代方程，输入迭代初始值0x，0y和00z= ，并通过迭代使那么综合考虑运算复杂度和反正切计算精度，设计方案中迭代次数n＝17。此外，由反正切函数的基本性质可知，在π/2±附近利用CORDIC算法实现反正切推算时，即便是耗费大量的FPGA资源也无法达到收敛的目的，这样会导致在π/2±和π±附近的角度值无法正确解算。[0,π/4]对应的反正切值是[0,1]，在此范围内进行CORDIC基本运算，可以简化FPGA中数据例化的复杂度，节约FPGA资源。而且，根据文献[20]所阐述的CORDIC象限扩展处理方法，任意[0,2π]范围内的反正切计算可以转换到[0,π/4]范围内进行计算，保证了角度值的计算收敛。因此，本文所提出的基于FPGA的相关法测量相位差技术方案初步将测量范围限定在[0,π/4]，即0~45°范围之内。

3 实验

根据本文所提出的基于FPGA的相关法测量相位差技术方案，研制出的原理样机实物如图7所示，电路板尺寸为10.0 cm×8.8 cm。原理样机上电工作时，每秒输出一个测量结果。为了测试本文设计方案的有效性，搭建了原理样机测试平台如图8所示。以GPS时间频率参考接收机Agilent/HP 58503输出的10 MHz作为双通道函数信号发生器SDG5162的外标，然后设置SDG5162输出两路存在某个特定相位差值的100 Hz的正弦波作为测量对象。两路正弦波幅度不要求严格相等，但要求不能超过±2.5 V输入电压范围。本实验中两路正弦波的幅度值皆设定为2 V。使用FPGA调试软件SignalTap II可以观察原理样机实时测量结果（如图9所示），或者在计算机上安装串口调试工具用于接收和查看测量结果。

图7 原理样机实物

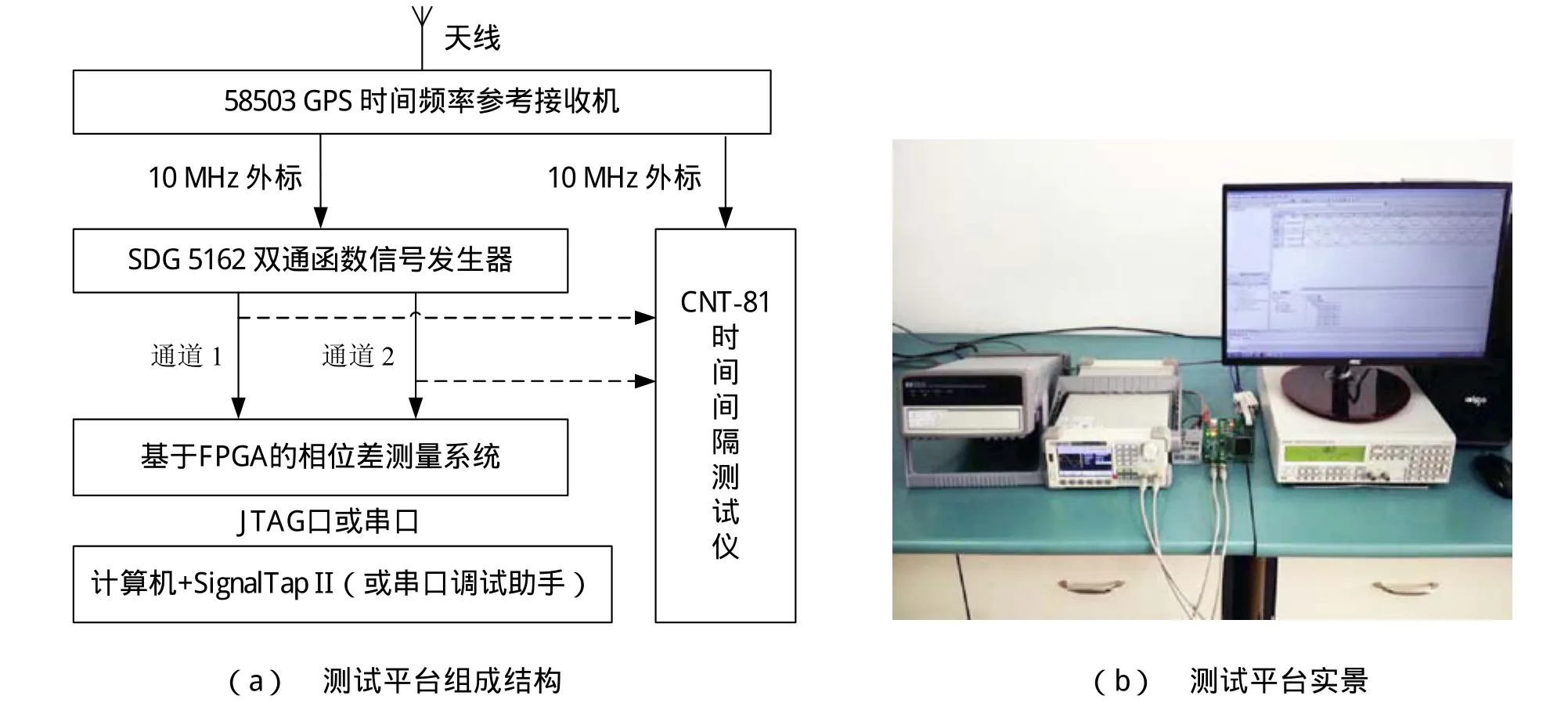
图8 原理样机测试平台

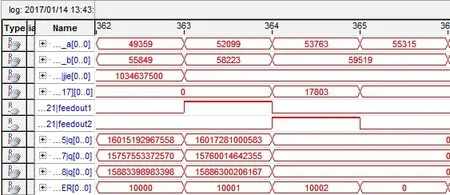
图9 使用Signal Tap II观察测量结果

考虑到函数信号发生器SDG5162两个输出通道存在差异，实验过程中同时使用Pendulum公司的时间间隔测试仪CNT-81（相位差测量分辨率为0.001°）测量双通道输出信号的相位差，并以CNT-81的测量结果作为SDG5162双通道输出的实际相位偏差。实验测试结果如表1所示，其中Djset为SDG5162输出两路弦波信号设定的相位差值，Djreal为CNT-81测得的实际相位偏差。Djm为系统测量值，Erela为测量相对误差。可见针对100 Hz的低频弦波信号，在0~45°范围之内原理样机测量相对误差不大于1.4%。

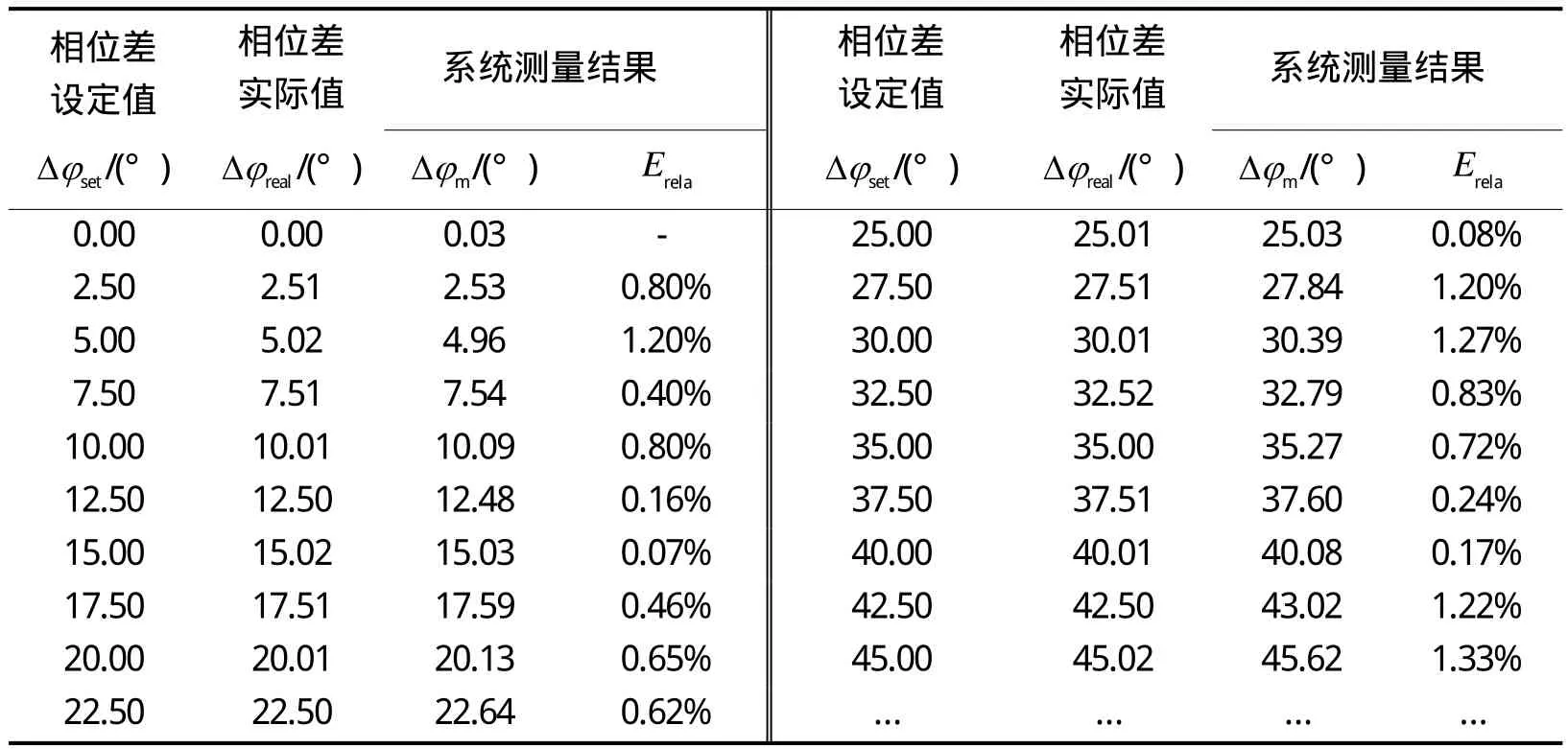
表1 原理样机测试结果

4 结语

为了实现弦波信号相位差的快速、准确地测量，本文提出一种基于FPGA的相关法技术方案。利用同步采样技术，将待测两路弦波信号转化为数字量，然后送至FPGA实施相关分析、反正切变换等不同形式的信号处理，完成相位差的测算。FPGA实现信号处理依赖于硬件描述语言在芯片内部构件并行处理的逻辑电路，在实现较好的测量精度的前提下满足了系统测量的实时性要求。实验结果表明，原理样机每秒输出一个测量结果，针对100 Hz的低频弦波信号，在0~45°的测量范围之内，测量相对误差小于1.4%。同时，该测量方案具备了体积小、便携性好的特征，原理样机电路板尺寸仅为10.0 cm×8.8 cm。整体设计方案，有望为相位差测量领域提供技术参考。

参考文献：

[1] BERTOTTI F L,HARA M S,ABATTI P J.A simple method to measure phase difference between sinusoidal signals[J].Review of ScientificInstruments,2010,81(11),115106:1-4.

[2] 杨俊,武奇生,孙宏琦.基于相关法的相位差检测方法在科氏质量流量计中的应用研究[J].传感技术学报,2007,20(1):138-145.

[3] 刘娅,李孝辉,王国永,等.一种频标信号数字化测量仪器的研制[J].时间频率学报,2015,39(2):73-81.

[4] VUCJIJAK N M,SARANOVAC L V.A simple algorithm for the estimation of phase difference between two sinusoidal voltages[J].IEEE Transactions on Instrumentation and Measurement,2010,59(12):3152-3158.

[5] 沈廷鳌,涂亚庆,李明,等.基于相关原理的相位差测量改进算法及应用[J].振动与冲击,2014,33(21):177-182.

[6] KIM D H,AHN B J.Phase measurement and error analysis in the arc-tangent method using a novel phase-compensating algorithm[J].Measurement Science and Technology,2013,24(10),105009:1-7.

[7] KOKUYAMA W,NOZATO H,OHTA A,et al.Simple digital phase-measuring algorithm for low-noise heterodyne interferometry[J].Measurement Science and Technology,2013,27(8),085001:1-8.

[8] KAWAGOE J,KAWASAKI T.A new precision digital phase meter and its simple calibration method[J].IEEE Transactions on Instrumentation and Measurement,2010,59(2):396-403.

[9] 曹鹏,费元春.孔径抖动对中频采样系统信噪比影响的研究[J].电子学报,2004,32(3):381-383.

[10] 陈宁,费元春.高速数据采集系统中的孔径抖动[J].北京理工大学学报,2003,23(2):234-237.

[11] Texas Instruments.Analog-to-Digital Converters ADS8364(Literature Number:SBAS219C)[Z].USA:Texas Instruments,2006.

[12] VOLDER J E.The CORDIC trigonometric computing technique[J].IRE Transactions on Electronics Computers,1959,8(3):330-334.

[13] WALTHER J S.A unified algorithm for elementary functions[J].Spring Joint Computer Conference Proceedings,1971,38:379-385.

[14] 刘小会,许蕾,刘海颖,等.基于CORDIC改进算法的反正切函数在FPGA中的实现[J].计算机技术与发展,2013,23(11):103-107.

[15]张建斌,梁芳,刘乃安.一种改进型CORDIC算法的FPGA实现[J].微电子学与计算机,2010,27(11):181-184.

[16]张朝柱,韩吉南,燕慧智.高速高精度固定角度旋转CORDIC算法的设计与实现[J].电子学报,2016,44(2):485-490.

[17] BHURIA S,MURALIDHAR.FPGA implementation of sine and cosine value generators using cordic algorithm for satellite attitude determination and calculators[C]//Proceeding of International Conference on Power,Control and Embedded Systems(Embedded Systems II),2010,177:1-5.

[18] SHANMUGA K M,MOHAMED A BM,NOOR M S.High precisionand high speed handheld scientific calculator design using hardware based CORDIC algorithm[C]//Proceeding of International Conference on Design and Manufacturing,2013:56-64.

[19] TIWARI V,KHARE N.Hardware implementation of neural network with sigmoidal activation functions using CORDIC,Microprocessors and Microsystems[J].2015,39(6):373-381.

[20] 宋晓梅,朱辉,王文静.基于CORDIC的旋转变压器解码算法研究[J].电子测量技术,2010,33(6):39-43.