基于不同轨道类型BDS卫星的载波相位共视时间传递分析
李雯,李伟超,葛玉龙
(1.中国科学院 国家授时中心,西安 710600;
2.中国科学院 精密导航定位与定时技术重点研究室,西安 710600;3.中国科学院大学,北京 100049)
0 引言
高精度时间传递在国民经济发展中的地位日趋重要,高新技术产业诸如通信、电力、交通、高速数字网同步等领域越来越依赖于高精度时间频率。
目前,GPS共视(CV,common-view)方法、全视(AV,all-in-view)方法和精密单点定位(PPP,precise point positioning)方法都广泛应用于远程时间比对。GPS CV和AV方法主要是使用伪距观测值进行时间传递。由于伪距观测值的噪声较大,因此时间传递的精度较低,在纳秒量级。随着具有高精度载波相位数据处理技术的发展,相关学者提出了GPS载波相位共视GPS CP(CV)(carrier phase common-view)方法,使用伪距和载波相位观测联合来进行时间传递,精度可达到亚纳秒量级[1-4]。
随着中国北斗卫星的发展,基于BDS卫星进行时间传递已成为一个重要的研究方向。目前,基于北斗CV模式的时间传递可以达到纳秒量级,北斗PPP时间传递结果精度和GPS PPP基本相当,可以达到亚纳秒量级。本文结合BDS CP(CV)模型,使用国际多模GNSS实验工程MGEX(malti-GNSS experiment)提供的精密轨道和钟差产品,研究分析GEO,IGSO和MEO这3种北斗在轨卫星进行时间传递的不确定度。本文使用GNSS多模双频接收机的载波相位观测数据,相对于双向卫星比对结果和光纤比对结果,计算BDS CP(CV)时间传递结果的标准差,并且通过计算修正Allan方差来分析BDS CP(CV)时间传递的稳定度。
1 BDS CP(CV)时间传递方法
1.1 BDS CP(CV)数学模型
BDS非差伪距和载波相位观测方程为:

式(1)和(2)中,ρ为测站r至卫星s的几何距离;r为测站序号;s为卫星序号;j为频率序号;和分别为测站r至卫星s第j个频率的码伪距和载波相位观测值;zpdδ和zpwδ分别为对流层天顶方向干延迟与湿延迟;分别为对流层干、湿延迟映射函数;为测站r至卫星s第 j个频率站星视线方向的电离层延迟;rd和分别为接收机和卫星端硬件延迟偏差;N为模糊度参数;rt为接收机钟差;st为卫星钟差;ε为观测误差。
在站间单差模式下求解两地时间差(未校准),由于伪距观测精度较差,因此本文联合使用载波相位观测值与伪距观测值。利用精密星历和卫星钟差解算接收机钟差,将伪距观测方程和载波相位观测方程分别形成无电离层组合消除一阶电离层延迟:

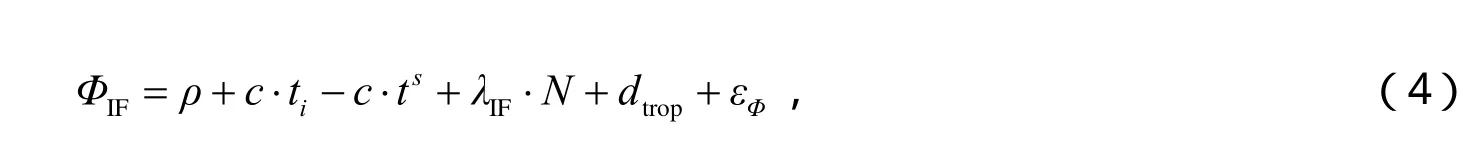
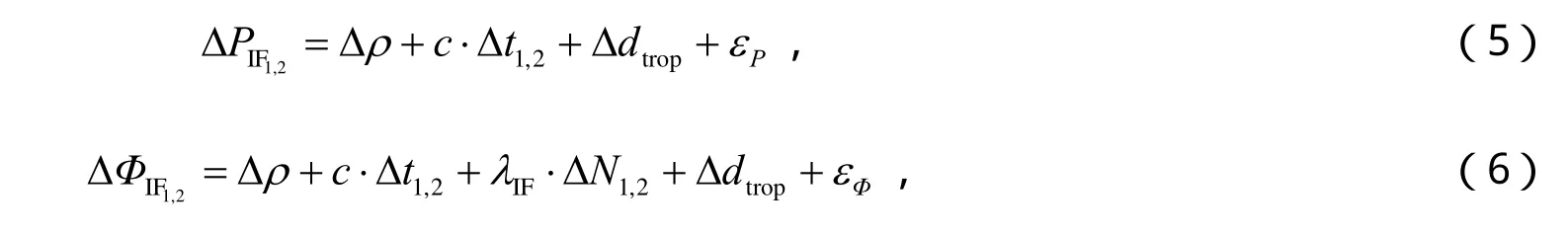
式(5)和(6)中,下标的1和2表示两个站。
在长基线中,电离层延迟可以通过消电离层组合消除,对流层影响比较明显,对流层的干分量可以通过模型改正,但是湿分量无法精确改正,本文引入GPS PPP解算的对流层延迟作为已知值。假设一个站点坐标精确已知,另一个站点坐标未知。组成误差方程:

式(7)中,V是残差,B是坐标改正系数,A是钟差系数,求解出来的钟差单位为m,C是消电离层组合波长,X是位置改正数,L是观测量。
1.2 数据预处理及参数估计
BDS数据处理中误差改正模型及参数估计如表1所示,其中,GBM是GFZ(The German Research Center for Geosciences,德国地学中心)提供的精密产品。

表1 误差处理策略
一阶电离层通过消电离层组合进行消除。对于双频非差相位数据的周跳探测,本文综合采用M-W组合、电离层残差组合和G-F组合[5]。GPS PPP解算的对流层延迟作为已知值。在静态BDS CP(CV)数据处理中,待估参数包括钟差参数和N个浮点模糊度参数。
本文采用Kalman滤波进行参数估计。在Kalman滤波过程中,BDS伪距观测值的精度设为0.6 m,载波相位观测值的精度设为0.004 m,并且按照BDS中3种在轨卫星GEO,IGSO和MEO的轨道与钟差精度的不同来设置合适的权比。
2 数据处理及时间传递不确定度评估方法
2.1 数据描述
本文采用Trimble接收机接收西安、临潼、长春、三亚4个站连续10d观测GEO,IGSO,MEO 3种卫星的载波相位观测数据,并进行数据处理。观测数据采样间隔为30 s,精密轨道、钟差文件的采样间隔分别为15 min和30 s,BDS卫星天线相位中心PCO和PCV改正采用MGEX的方法改正[6]。
2.2 数据处理
双向卫星时间频率传递方法使用原子钟产生的载频信号和1 PPS信号作为参考信号。1 PPS信号是双向比对的被测对象,用于调制信号。站间互发互收数据并交换数据就可以求得站间钟差。目前双向卫星时间频率传递实现站间时间同步精度可达到亚纳秒量级[7]。
光纤双向比对法的基本原理是光纤一端记录某一时刻钟信息,同时另一端发送时间信号,待时间信号到该端记录此刻钟信息,通过对两钟信息的计算就可得两端钟差[8]。采用该传递方法,国内100 km高精度光纤时间传递的频率稳定度优于1×10-15/1d,时间同步精度可达100 ps量级[9]。
本文使用GNSS多模双频接收机的载波相位观测数据,相对于双向卫星比对结果和光纤比对结果,计算BDS CP(CV)时间传递结果的标准差;通过计算修正Allan方差来分析BDS CP(CV)时间传递的稳定度。数据处理的具体流程如下:① 用GPS PPP解算出站坐标和对流层。从目前IGS(International GNSS Service,国际GNSS服务组织)提供的对流层产品看,主要都是基于GPS卫星来解算的。相对于BDS PPP,GPS PPP解算的对流层精度更高。武汉大学分析中心在进行北斗定轨时都是以GPS PPP解算的站坐标和对流层作为已知值代入[10]。因此,GPS PPP解算的站坐标和对流层具有可用性;② 将第①步解算的站坐标和对流层作为已知值代入观测方程;③ 通过无电离层组合消除电离层延迟,分别计算出西安与其他3个站之间的时间差(包含硬件延迟);④ 分别将长春—西安和三亚—西安的载波相位时间传递结果与双向卫星比对结果作比较,将临潼—西安的载波相位时间传递结果与光纤比对结果作比较;⑤ 最后通过计算比较结果的标准差及修正Allan方差来分析评估BDS CP(CV)的不确定度。
2.3 时间传递不确定度评估方法
测量不确定度(简称不确定度)是表示测量分散性的概念,它表征了被测量的真值处于某个量值范围的一个估计。测量不确定度的评定方法通常可分为A类评定与B类评定两类。其中A类评定是指不确定度的分量由观测数据的统计分析得到;B类评定是指不确定度的分量是基于经验或其他数据认定的概率分布得到[11]。
BDS CP(CV)时间传递的不确定度由原子钟的稳定度和站间钟差解的精度及其所体现的频率稳定度共同决定。在原子钟稳定度确定的情况下,本文采用两种方法分析BDS CP(CV)时间传递的不确定度(A类不确定度):
① 通过计算CP(CV)时间比对结果与卫星双向比对结果或光纤比对结果差异的标准差来分析BDS CP(CV)时间传递的不确定度,标准差s的计算方法如下:

式(8)中,n表示样本数,ix表示钟差样本,表示解算后的钟差减去真值的均值:

式(9)中,m是平均因子,0t是最小测量间隔。
3 不确定度分析
3.1 标准差分析
本节使用标准差作为不确定度评估准则。西安与其他3个站之间的观测数据比对结果的标准差如表2所示。

表2 观测数据比对结果的标准差ns

图1 西安—长春IGSO观测数据比对相对于双向卫星比对的结果
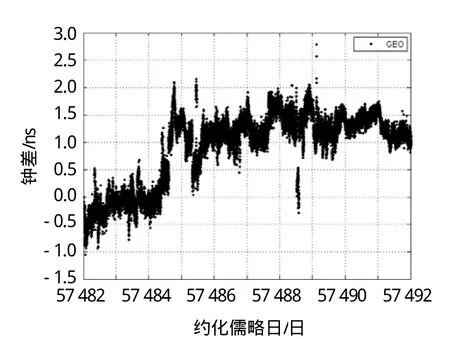
图2 西安—临潼GEO观测数据比对相对于光纤比对的结果
如表2所示,相对于双向卫星比对结果,西安—长春观测数据比对结果的标准差中IGSO较好,可以达到0.39 ns;相对于光纤比对结果,西安—临潼观测数据比对结果的标准差中IGSO较好,可以达到0.18 ns。所以,相对于双向卫星比对结果和光纤比对结果,采用IGSO载波相位时间传递结果的标准差较好。出现这种结果的原因可能由于GEO卫星轨道精度比较差。随着基线长度的增长,星历误差越大。本文通过站间差分后可以消除卫星钟差,只能消弱卫星轨道等误差的影响,但不能完全消除。西安—长春IGSO观测数据比对相对于双向卫星比对的结果如图1所示;西安—临潼GEO观测数据比对相对于光纤比对的结果如图2所示。
西安—三亚观测数据比对结果的标准差中IGSO和MEO较差的主要原因可能由于卫星数较少,观测弧段较短,一旦卫星全部失锁就会导致IGSO和MEO的观测数据不连续,滤波计算存在重新收敛,导致结果较差。
3.2 稳定度分析
BDS CP(CV)时间传递的稳定度采用Stable32软件及其修正Allan方差模型进行评估分析。基于GEO和IGSO观测数据比对结果的稳定度,我们分析15 d采集的所有观测数据;由于MEO观测卫星数较少,观测数据不连续,为了分析GEO,IGSO和MEO的观测数据比对结果的稳定度,我们选择同一弧段的观测数据。
图3和图4分别为西安—长春与西安—临潼观测数据比对结果稳定度。如图3和图4所示,基于GEO和IGSO的观测数据比对结果的稳定度相当。在西安—三亚的观测数据比对结果中,基于GEO的观测数据比对结果的稳定度比基于IGSO的较好,主要原因可能由于IGSO卫星数较少,观测弧段较短,其观测数据会因卫星失锁而出现不连续的情况,导致结果较差。基于GEO和IGSO的观测数据比对结果的稳定度如表3所示。

图3 西安—长春观测数据比对结果的稳定度

图4 西安—临潼观测数据比对结果的稳定度

表3 基于GEO和IGSO的观测数据比对结果的稳定度
图5和图6分别为西安—三亚观测数据比对结果的稳定度,西安—临潼观测数据比对结果的稳定度。如图5和图6所示,同一弧段的观测数据比对结果的稳定度。基于GEO和IGSO的观测数据比对结果的稳定度比基于MEO的较好。主要原因可能由于MEO每天只有六七个小时的观测数据,观测弧度较短,再次观测时滤波计算存在重新收敛,而GEO和IGSO只有在第1次观测时存在收敛,所以MEO在中间弧段收敛时间的观测数据解算结果较差。基于GEO,IGSO和MEO同一弧段的观测数据比对结果的稳定度如表4所示。

图5 西安—三亚观测数据比对结果的稳定度
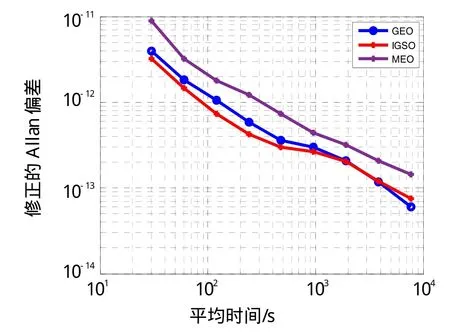
图6 西安—临潼观测数据比对结果的稳定度

表4 基于GEO,IGSO和MEO同一弧段的观测数据比对结果的稳定度

采样间隔τ/s 西安—临潼GEO IGSO MEO 30 3.945 8×10-12 3.269 4×10-12 8.873 2×10-12 60 1.843 7×10-12 1.473 9×10-12 3.250 6×10-12 120 1.059 8×10-12 7.368 8×10-13 1.788 3×10-12 240 5.833 0×10-13 4.256 8×10-13 1.226 1×10-12 480 3.592 9×10-13 3.004 9×10-13 7.407 9×10-13 960 2.986 7×10-13 2.650 5×10-13 4.434 2×10-13 1 920 2.085 5×10-13 2.056 8×10-13 3.174 8×10-13 3 840 1.179 3×10-13 1.197 8×10-13 2.068 3×10-13 7 680 6.002 5×10-14 7.582 0×10-14 1.432 4×10-13
综上站间观测数据比对结果的稳定度,基于GEO和IGSO的载波相位时间传递结果相对于双向卫星比对结果和光纤比对结果的稳定度比基于MEO的较好。
4 结论
本文首先介绍了基于不同卫星类型的BDS CP(CV)方法,并给出了各项数据误差改正模型,以及利用BDS CP(CV)进行时间传递及其不确定度评估的方法。文章采用Trimble接收机接收西安、临潼、长春、三亚4个站连续10d观测GEO,IGSO,MEO 3种在轨卫星的载波相位观测数据进行数据处理,并采用标准差以及修正Allan方差模型评估稳定度作为其不确定度(A类不确定度)的评定准则。实验结果表明:相对于双向卫星比对结果和光纤比对结果,基于IGSO载波相位时间传递结果的标准差较好,基于GEO和IGSO的载波相位时间传递结果的稳定度比基于MEO的较好。
参考文献:
[1] GUANG Wei,ZHANG Peng-fei,YUAN Hai-bo,et al.The research on carrier phase time transfer of BeiDou navigation satellite system[J].European Frequency and Time Forum(EFTF),2015:113-117.
[2] YAO J,SKAKUN I,JIANG Z,et al.A detailed comparison of two continuous GPS carrier-phase time transfer techniques[J].METROLOGIA,2015,52(5):666-676.
[3] DEFRAIGNE P,BRUYNINX C,GUYENNON N.PPP and phase-only GPS time and frequency transfer[J].IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum,2007:904-908.
[4] FUJIEDA M,PIESTER D,GOTOH T,et al.Carrier-phase two-way satellite frequency transfer over a very long baseline[J].METROLOGIA,2014,51(3):253-262.
[5] KONG Yao,YANG Xu-hai,CHANG Hong,et al.Method of precise common-view frequency transfer based on BeiDou GEO satellite[J].2014 IEEE International Frequency Control Symposium(FCS),2014:1-4.
[6] CAI C,GAO Y,PAN L,et al.Precise point positioning with quad-constellations:GPS,BeiDou,GLONASS and Galileo[J].Advances in Space Research,2015,56(1):133-143.
[7] LIN H T,HUANG Y J,TSENG W H,et al.Recent development and utilization of two-way satellite time and frequency transfer[J].Journal of Metrology Society of India,2012,27(1):13-22.
[8] JEFFERTS S R,WEISS M A,LEVINE J,et al.Two-way time and frequency transfer using optical fibers[J].IEEE Transactions on Instrumentation and Measurement,1997,46(2):209-211.
[9] 梁双有,任燕.利用光纤进行高精度时间传递[J].时间频率学报,2003,26(1):75-80.
[10] GUO Jing,XU Xiao-long,ZHAO Qi-le,et al.Precise orbit determination for quad-constellation satellites at Wuhan University:strategy,result validation,and comparison[J].Journal of Geodesy,2016,90(2):143-159.
[11] 魏亚静.一种导航系统时间溯源链路及其不确定度分析方法研究[D].西安:中国科学院国家授时中心,2016.

