C波段卫星双向时间传递的系统性能验证

杨朝中，王玉林，华宇，王伟

（1.中国科学院 国家授时中心，西安 710600；2.中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3.中国科学院大学，北京 100049）

0 引言

卫星双向时间频率传递（TWSTFT）是目前国际上远程时间频率标准之间比对精度最高的比对手段之一，中国科学院国家授时中心在全国建有6套卫星地面站观测系统，为了实现各个地面站的时钟同步，采用C波段TWSTFT进行远程时间频率传递；TWSTFT采用两站间互发互收的测量体制，消除了地面站站址误差、卫星星历误差、卫星转发器时延、对流层延迟等一些共同误差源影响，使时间比对精度得到大幅度提高[1]。

在6个地面站之间进行了TWSTFT后，需要分析6个地面站之间时间频率同步的性能，一般方法是选取传递精度比其高一个等级的时间源来进行验证，目前主要的远距离时间传递方法有：搬运钟、全球卫星导航系统（GNSS）、卫星双向、光纤、激光时间传递等手段。时间精度比卫星双向高的有光纤和激光时间传递，对于长基线时间传递，光纤时间频率传递很难实现千公里级以上的高精度传递，激光时间频率传递对应用条件要求非常苛刻，且成本高昂[2]，都无法满足要求。为了验证6个卫星地面站观测系统C波段TWSTFT的性能，本文设计了一种三站闭合检验方法验证其性能。

1 卫星双向的基本原理

1.1 基本原理

基于通信卫星的双向时间频率传递基本原理如图1所示。卫星双向时间频率传递系统一般由调制解调器、时间间隔计数器、甚小口径卫星终端站等设备构成。

图1 卫星双向原理图

卫星双向的基本原理是在地面站A的1PPS时钟信号被调制在一个中频载波信号上，经上变频器将载波信号频率上变频，再经功放放大后将调制信号发送至卫星，卫星接收到信号后使用转发器将信号广播至地面。地面站B接收到经由卫星转发的来自地面站A的信号后，先使用低噪声放大器将信号放大，再通过下变频器将信号下变频到中频信号，然后再解调信号，最后在站B使用伪码相关原理测出时差。同时站B也向站A发送信号，站A接收信号后也测出时差[2-3]。

TWSTFT的计算方法如下：

式（1）和（2）中，TTICA和TTICB是时间间隔计数器的读数；TA和TB是两站各自的钟面时间，dTA和dTB是发射机时延；dAS和dBS是上行链路时延；dSBA和dSAB是卫星转发器时延；dSA和dSB是下行链路时延；dRA和dRB是接收机时延；SA和SB是Sagnac效应修正，是由于地球自转引起的相对论修正，SB=−SA，SA的含义是信号从A站出发到达卫星，转发后再到达B站总共的Sagnac效应。2ωApc2为Sagnac效应计算公式，ω为地球自转角速度7293115×10-11rad/s，Ap为地球站、卫星和地心构成的三角形在赤道平面上的投影面积，c为光速299 792 458m/s。由式（1）和（2）可以推导出：

表1是式（3）中各项的注释。

表1 TWSFTF公式中各项的注释

TTICA和TTICB的值在正常情况下总为正，对GEO卫星来讲，信号从地面到卫星再返回地面，所需时间一般约为0.25s；对MEO卫星所需时间约为0.15s。对于TWSTFT，一般在正式比对前，实现两站原子钟的粗同步，精度在1ms之内[4]。

地面站设备时延的计算，可通过事先测量得到；空间传播时延包括：几何路径时延、电离层时延和对流层时延。对流层时延可以完全抵消；电离层时延在后面文章中详细说明；卫星转发器时延可以完全抵消；Sagnac效应的计算可通过公式准确计算出。

1.2 误差分析

由1.1节可知，卫星双向的主要误差来源为设备时延、几何路径时延、电离层时延、对流层时延、卫星转发器时延和Sagnac效应；其中，地面站设备时延可通过事先测量得到；对流层时延和卫星转发器的时延由于卫星双向链路的对称性可以完全抵消[5]。

几何路径时延的误差主要是由卫星轨道测定误差引起的，本文所使用的轨道数据来自中国科学院国家授时中心转发式测定轨系统，通过转发式测定轨方法进行动力学统计定轨得到的。该方法测距精度高，单次伪距测定精度优于1cm，1d观测弧段的定轨观测残差优于9cm，对同步卫星的定轨精度可达到2m水平，本文试验中的轨道数据精度在米级水平，星地连线方向上的轨道精度在分米级，残余时延约0.3ns[6]。

地固系下地面站坐标为（x1，y1，z1），卫星坐标为（x2，y2，z2），Sagnac效应可由如下公式求得：

则有：

式（4）至（7）中：ω为地球自转角速度7 293 115×10-11rad/s，Ap为地球站、卫星和地心构成的三角形在赤道平面上的投影面积，c为光速299 792 458 m/s。

由于GEO卫星相对于地球静止不动，Sagnac效应的日变化量对双向的影响小于0.1ns。

在卫星双向时间比对过程中，由于上下行频率不相等，本文试验采用的是C波段，上行约为6 GHz，下行约为4 GHz，计算时需要考虑电离层时延的影响，在TWSTFT中最常采用的是国际GNSS服务组织（IGS）发布的电离层产品；电离层延迟计算公式如下[7-8]：

式（8）中，c为光速，f为系统工作频率，QTEC为IGS发布的产品电离层电子总含量（TEC，total electron content）。IGS提供电离层网格精度约为2~8 TECU（1 TECU表示单位体积包含1016个电子），数据有效性不会优于80%[9]，经过修正后C波段电离层的残余时延约0.4 ns[6]。

2 三站闭合差试验方法

本文选取西安—喀什和西安—三亚两条长基线进行试验；选取中星12号地球同步轨道（GEO）卫星作为卫星双向观测的卫星。

采用三亚站（6号站）、西安站（3号站）以及喀什站（5号站）的GEO–3.7 m口径天线进行两站间的卫星双向比对，即每个站都同时收另外两个站的发射的信号（采用的观测设备为3通道设备，即可以同时接收3路不同的信号），如图2所示。

设Tn为n号站的钟面时刻，则根据6号站和3号站的观测数据可以得到6号和3号站的钟差（T3－T6）；同理，根据3号站和5号站的观测数据可以得到3号站和5号站的钟差（T3－T5）；根据实际测得的（T3－T6）和（T3－T5）可以归算得到6号站和5号站的钟差（T6－T5）（归算钟差）＝（T3－T5）－（T3－T6）；同时，根据6号站和5号站的观测数据可以求得6号站和5号站的钟差（T6－T5）（实测钟差）；将（T6－T5）（归算钟差）和（T6－T5）（实测钟差）相减得平均值即为比对的准确度。

由于三亚、西安和喀什各站均配备有2套GEO观测设备，各站均简称为G1天线和G2天线，本文分别使用G1和G2天线系统进行了三站闭合差试验。在本文试验期间除因设备检修和天气等原因外，各站的G1天线观测方式为全天观测中星12号卫星；各站的G2天线观测方式为四星轮转，每2h将4颗GEO卫星（中星12号，中星10号，马星2号，亚太7号）遍历一遍。

图2 三站闭合差原理示意图

3 数据处理

本文对2016年12月17日至28日部分时间段的数据按试验方法进行处理，3个地面站同时对中星12号卫星进行连续观测。

3.1 G1天线数据分析

图3和图5为G1天线不同时段喀什—三亚卫星双向钟差示意图，图中上面的线表示实测钟差，下面的线表示归算钟差，图3中G1天线设备的系统差没有扣除。

根据移动标校站测得的G1天线设备系统误差为7.56ns，除去设备系统误差可得三站闭合差数据的均方根值（RMS）如图4和图6所示。

图3 UTC时间2016年12月19日至23日G1天线喀什—三亚卫星双向钟差

图4 UTC时间2016年12月19日至23日G1天线喀什—西安—三亚卫星三站闭合差

图5 UTC时间2016年12月26日至28日G1天线喀什—三亚卫星双向钟差

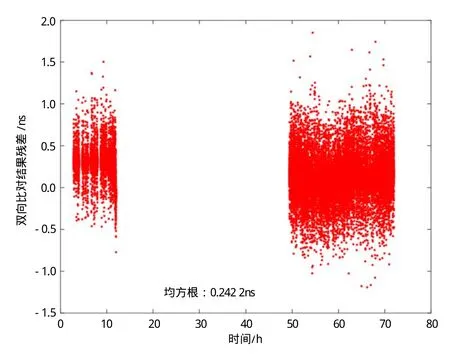
图6 UTC时间2016年12月26日至28日G1天线喀什—西安—三亚卫星三站闭合差

3.2 G2天线数据分析

图7和图9为G2天线不同时段喀什—三亚卫星双向钟差示意图，图中上面的线表示实测钟差，下面的线表示归算钟差，图7中G2天线设备的系统差没有扣除。

根据移动标校站测得的G2天线设备系统误差为1.57 ns，除去设备系统误差可得三站闭合差数据的RMS如图8和图10所示。

图7 UTC时间2016年12月17日至23日G2天线喀什—三亚卫星双向钟差

图8 UTC时间2016年12月17日至23日G2天线喀什—西安—三亚卫星三站闭合差

图9 UTC时间2016年12月25日至28日G2天线喀什—三亚卫星双向钟差

图10 UTC时间2016年12月25日至28日G2天线喀什—西安—三亚卫星三站闭合差

3.3 讨论

由图4，6，8和10可以看到双向比对结果残差的稳定性较好，但是也有相当数量的奇异值，这些主要是由于设备的不一致性及环境差异较大造成的。

由于在本次试验中G1天线和G2天线的系统差采用移动标校站事先测得，非实时测得，所以在实验时系统差可能会有变化，但是只要系统的设备不发生变化，系统差变化非常小，属于亚纳秒量级，对最终结果影响非常小。

4 结语

本文利用国家授时中心新建的卫星观测系统，进行了卫星双向时间频率传递时延，并且描述了三站闭合差的测量模型，基于C波段信号，给出了利用中星12号GEO卫星进行卫星双向时间频率传递的最新测量结果。使用国内3个地面观测站的GEO天线观测数据计算得到三站闭合差数据均优于1ns。从三站闭合差的测量模型可以得知其误差来源与卫星双向的误差来源是一致的，测量精度也与卫星双向一致；利用三站闭合差是可以验证卫星双向时间传递系统的性能。

参考文献：

[1] 李志刚,乔荣川,冯初刚.卫星双向法与卫星测距[J].飞行器测控学报,2006,25(3):1-6.

[2] 武文俊.卫星双向时间频率传递的误差研究[D].西安:中国科学院国家授时中心,2012.

[3] ITU-R.TF.1153-2.The operational use of two-way satellite time and frequency transfer employing PN codes[S].2003.

[4] 李孝辉,杨旭海,刘娅,等.时间频率信号的精密测量[M].北京：科学出版社,2010.

[5] 刘利,韩春好.卫星双向时间比对及其误差分析[J].天文学进展,2004,22(3):219-226.

[6] 韦沛.基于GEO通信卫星的转发式共视授时方法[D].西安:中国科学院国家授时中心,2013.

[7] 孔垚,杨旭海,孙保琪,等.基于“北斗”观测数据的C波段双向卫星时间频率传递中的电离层改正[J].时间频率学报，2012,35(3):148-155.

[8] SCHAER S,GURTNER W.IONEX:The IONosphereMap Exchange Format Version 1[S].Berne,Swiss:University of Berne,1998.

[9] 王刚,魏子卿.格网电离层延迟模型的建立方法与试算结果[J].测绘通报,2000,9:1-2.