滚珠丝杆副的振动实验测试系统及适配性评价*
温振强,王天雷,陈惠添,赵 挺,王 柱
0 引言
数控机床进给系统的功能是控制刀具运动到设定位置,确保加工工件尺寸、位置和表面精度。滚珠丝杠副作为数控机床进给系统的关键功能部件,其性能的高低很大程度上决定了数控机床的精度水平[1-2]。评价丝杠性能的主要指标有振动、噪音、摩擦力矩温升、刚度、寿命等,都要受到进给运动的传动精度、灵敏度和稳定性的直接影响。其中丝杠的振动除与制造和安装水平的直接相关以外,文献[3-6]表明,滚珠对返向器的冲击是产生轴向振动重要因素,将直接影响机床进给精度,导致工作台产生轴向位移,影响工作台的定位精度。而丝杠的径向振动也可能作为一个激励源,使机床进给系统甚至整机在某一频域内产生共振,加剧刀具的磨损,增大表面粗糙度,产生波纹和无法保证尺寸精度等,影响零件的加工质量。
随着数控机床向高速、高精方向发展,对滚珠丝杠副的性能提出了越来越高的要求,作为功能部件之一,滚珠丝杠副在机床整机中起到关键作用,在保证机床实现客户要求的前提下,尽可能使滚珠丝杆与整机功能及性能指标相匹配,避免精度冗余或不足,提高产品性价比。
根据上述要求,本文设计了一种适合企业进行滚珠丝杆振动测试的系统,该系统由运动控制器、多通道数据测量分析仪、加速度传感器和负载等组成,并针对公司面向不同产品加工的数控机床对滚珠丝杆的差异性要求,对三个不同品牌滚珠丝杆副运行的振动性能进行了测试、分析和适配性评价,为设计不同用途的数控机床/装备选配滚珠丝杆副提供依据。
1 测试装置
1.1 测试装置结构设计
滚珠丝杆振动测试系统见图1,主要由伺服电机及驱动器、加速度传感器和控制系统等组成。其中运动控制选用固高公司GTS-800-PV/PG-PCI型运动控制器,信号采集与分析采用美国Benstone公司四通道动态信号测量仪、传感器采用美国PCB公司LW185401/02/03三轴加速度传感器,数控系统采用公司自主研发的佳铁系统(JT803),此外,设计了进给系统负载,可模拟数控机床实际加工状况进行加载运行。测试系统基本构成见图2。

图1 滚珠丝杆副振动测试系统
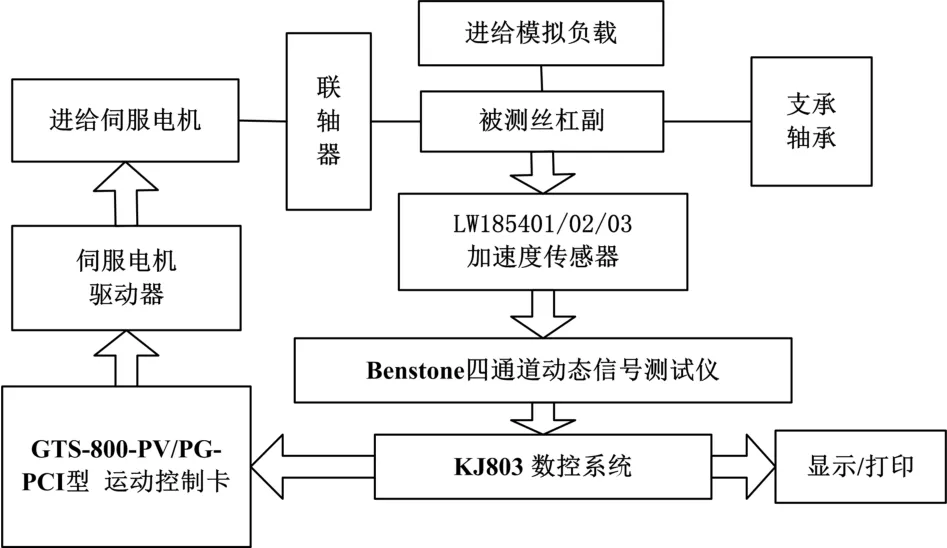
图2 滚珠丝杆副振动测试系统基本构成
1.2 软件设计
滚珠丝杆振动性能测试系统软件设计见图3,主要由驱动模块,控制系统,数据采集分析模块等组成。

图3 测试系统程序总体设计框图
2 测试试验
本文仅针对公司生产的500C/E高光数控机床的配套的X轴滚珠丝杆,选择不同品牌滚珠丝杆进行振动测试,分析与评价其对高光数控机床的适配性。本文仅对滚珠丝杆在不同转速时产生的振动进行测试,并不考虑产生振动的原因,即激励因素,或进行故障诊断分析。因此测试时,采集时域中加速度幅值信号进行分析,对振动不做频域分析。
测试安排如下。
(1)测试装置
测试采用公司研发的滚珠丝杆副振动性能测试系统,见图1。滚珠丝杠两端支撑方式为双推—支承方式,即丝杠一端固定,另一端支承。固定端轴承同时承受轴向力和径向力,支承端轴承只承受径向力,而且能作微量的轴向浮动,可以避免或减少丝杠因自重而出现的弯曲。同时丝热变形可以自由地向一端伸长。在被测丝杠螺母上安放了LW185401三轴加速度传感器测量丝杠振动,运行时分别采集径向水平、垂直和轴向的振动信号,如图4所示。
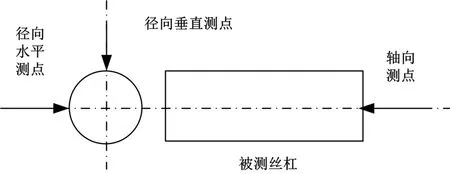
图4 滚珠丝杆副振动测试系统
(2)测试对象
针对500C/E高光数控机床的X轴滚珠丝杆,选取市场三个使用较广的品牌,分别编号为:1#丝杠、2#丝杠和3#进行测试,被测滚珠丝杆主要参数均为:公称直径d0=28 mm,滚珠直径db=3.5 mm,导程I=5 mm,丝杠最大行程Lmax=800 mm,返向器为内循环式,滚珠直径为3.175 mm。
(3)测试方案
根据公司产品500C/E高光数控机床设计要求,切削加工时进给速度范围为:0.25~10 m/min;快速进给时为:10~40 m/min。此外,另选高速状态,即进给速度为100 m/min(2 000 r/min)进行测试,分别选定三种速度为滚珠丝杠的测试转速,见表1。测试时,将有预加载荷的滚珠丝杆安装在丝杆性能平台上,通过驱动单元驱动丝杆,往返跑合丝杆,在稳定运行后进行曲线录取与数据存储,数据采集模块采集丝杆3次往返加速度幅值。

表1 测试转速的选取r/min
3 试验结果与分析
3.1 试验结果
在转速为200、800与2 000 r/min进行测试,对不同滚珠丝杆进行3次往返运行,将测试的加速度幅值取均值和最大峰值列入表2。图5、图6与图7是在转速为200 r/min滚珠丝杆在时域里的轴向振动、径向水平振动和径向垂直振动波形,分析表2与图5~7可知。
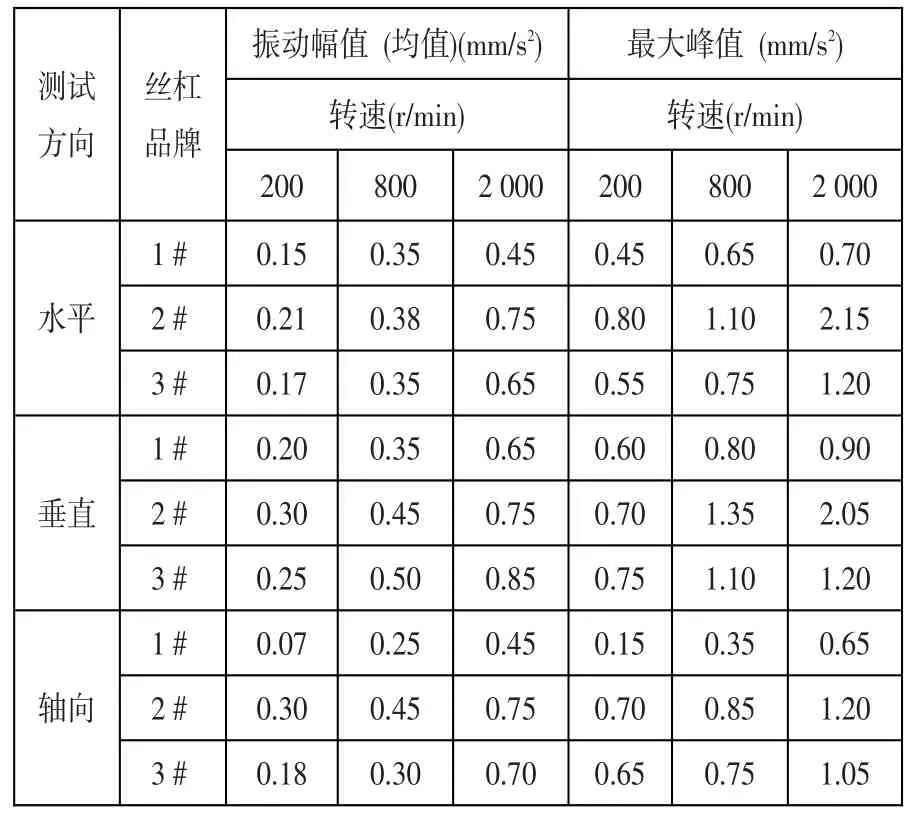
表2 三种品牌测试结果
(1)对比表2中三个不同转速测试数据,1#滚珠丝杆副的轴向振动、径向水平振动与径向垂直振动的振幅均值、峰值都小于2#丝杆副和3#丝杆副。
(2)对不同转速丝杆副的测试表明,轴向振幅<径向水平振幅<径向垂直振幅。即,滚珠丝杆轴向振幅小于径向振幅。
(3) 图 5~7 为 转 速 在200 r/min(对应的进给速度为10 m/min)时,在时域里采集不同丝杆的三个方向振幅变化曲线,可看出:2#滚珠丝杆振幅均大于1#和3#丝杠。
(4)表2与图5、图6和图7表明,三种丝杠都有显示出峰值,有冲击,不存在明显规律。丝杠1#三个方向的最大峰值均小于1,丝杠2#的最大峰值比丝杠3#最大峰值大。
(5)随着转速的提高,滚珠丝杠副三个方向振动幅值均增大。
(6)整体评价滚珠丝杠副振动性能,并按优劣排序为:1#丝杠>3#丝杠>2#丝杠。
3.2 丝杆性能分析及适配性评价
滚珠丝杠的轴向振动是影响定位精度和噪声的重要因素[4],数控机床的X、Y轴的丝杠振动会影响加工零件的水平投影轮廓的尺寸精度误差和表面精度,Z轴丝杠振动可能导致工件表面粗糙度值增大或产生波纹[5-7]。
为较客观地评价滚珠丝杠振动特性,应考虑在不同转速和不同的方向振动对整机加工精度与工作稳定性的影响程度不一样,因此,本文采用加权平均的综合评价法对三种丝杠振动性能进行优劣排序。权重的确定如下。
(1)振幅方向权重的确定。用加权平均值来评价丝杠振动特性的优劣,考虑轴向振动对加工质量影响最大,取加权系数为0.4,径向垂直和水平均取0.3。
(2)不同转速所测振幅的权重的确定。考虑转速200 r/min时,对应的进给速度为10 m/min,为高速加工一个重要指标,因此取加权系数为0.5;800 r/min为空行程快速定位,取加权系数取0.3;,2000 r/min为特别设定高速,仅作评价参考,取加权系数为0.2。
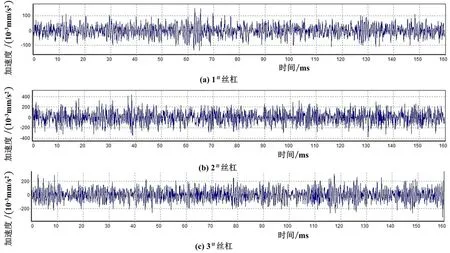
图5 滚珠丝杠副轴向振动波形(n=200 r/min)
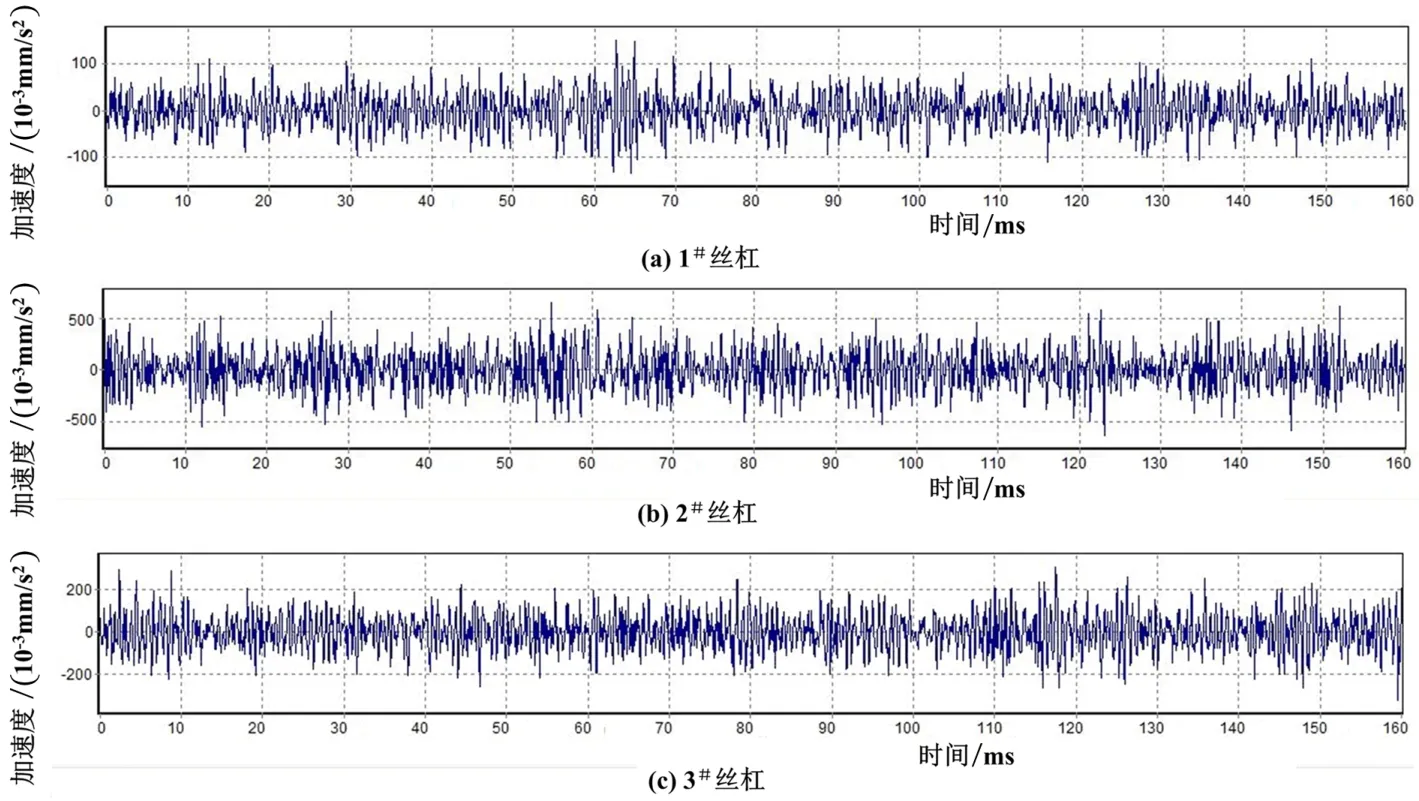
图6 滚珠丝杠副径向水平振动波形(n=200 r/min)
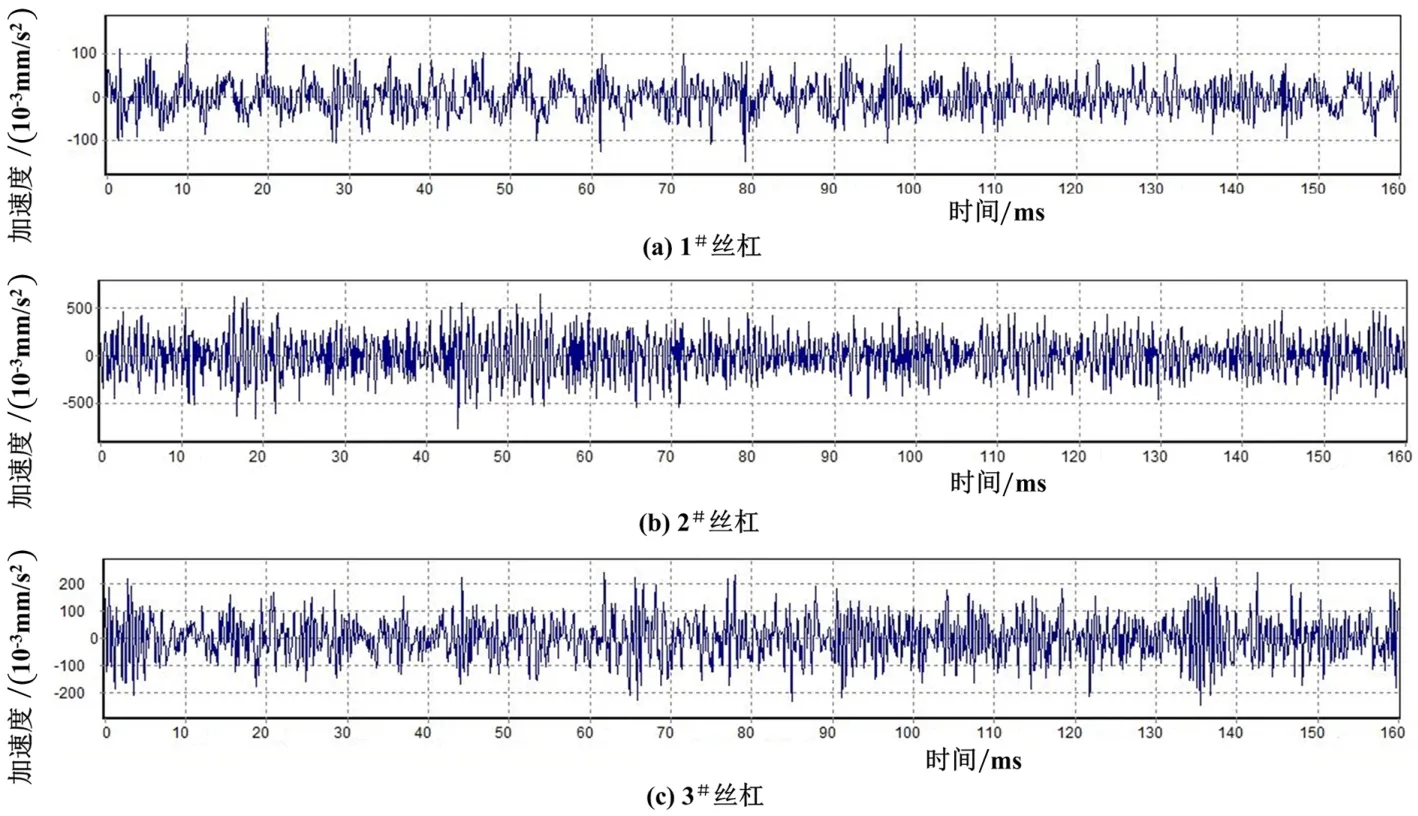
图7 滚珠丝杠副径向垂直振动波形(n=200 r/min)
综合评价计算公式:

其中:Aˉi分别为各丝杠振幅加权平均值,当i=1时为1#丝杠振幅加权平均值,其他以此类推;aijk为i丝杆在j方向,对应的k转速时滚珠丝杆测得振幅;j为滚珠丝杆测得的轴向、径向水平和径向垂直三个方向振幅测试;k为对应的转速在200 r/min、800 r/min和2000 r/min时滚珠丝杆测试;wj为轴向振幅、径向水平振幅和径向垂直振幅的加权系数,分别为:0.3、0.3和0.4。
最大峰值取各个丝杠在不同测试状态所采集的振幅最大峰值,进行简单的数学平均,公式为:
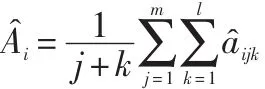
Aˆi分别为各丝杠最大峰值的平均值;aˆijk为i丝杆在j方向,对应的k转速时滚珠丝杆测得最大峰值。
根据表2数据分别计算 Aˉi、 Aˆi,结果列入表3,由表3可明显看出优劣排序为:1#丝杠>3#丝杠>2#丝杠。
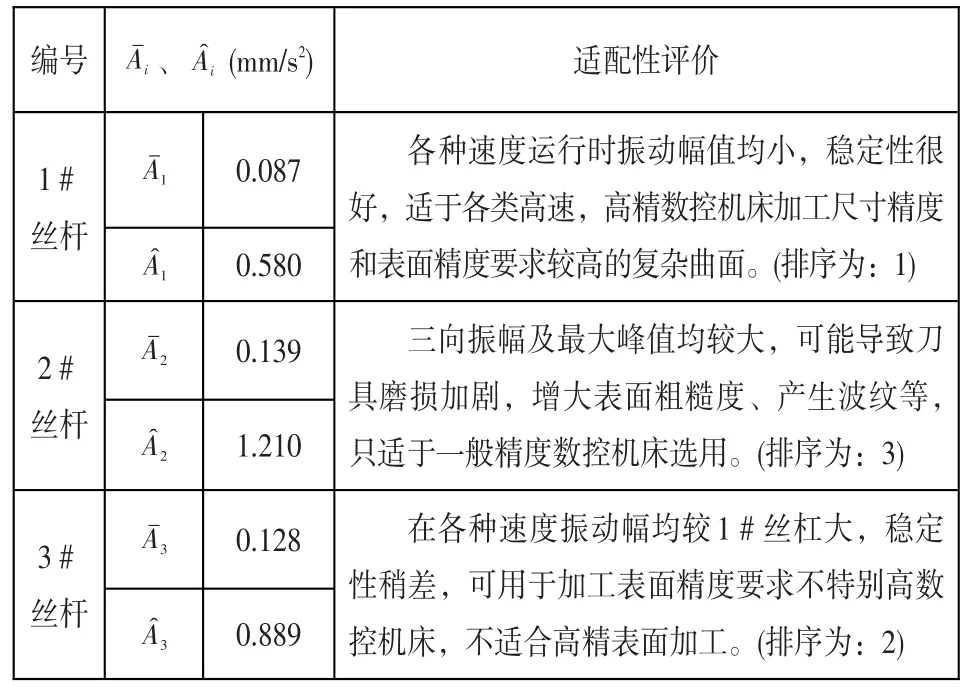
表3 丝杆振动性能综合评价及适配性评价
4 结语
(1)针对各种数控机床对滚珠丝杆的不同要求,设计了一种适合企业进行滚珠丝杆振动测试系统平台,该平台配置其他测试附件,还可用于测试丝杠的噪音、摩擦力矩、温升、刚度、寿命等。
(2)对三个不同品牌滚珠丝杆副进行了测试,并采用加权平均的综合评价法对三种丝杠振动性能进行优劣排序。较客观地区分不同品牌丝杆振动性能差异。
(3)分析了不同丝杠与面向不同加工对象的数控机床的适配性,为设计数控机床/装备选配滚珠丝杆副提供了依据。
对不同品牌的电机进行测试,分析与客观评价了伺服电机的整体性能,为企业生产的不同数控机床/装备选择适配滚珠丝杆副提供了可靠客观依据,有效提高了数控机床/装备的性价比,为企业创造了较大的经济效益。
参考文献:
[1]黄祖尧.精密高速滚珠丝杠副的最新发展及其应用[J].航空制造技术,2003(4):36-40.
[2]张佐营,宋现春,姜洪奎.精密滚珠丝杠副轴向振动激励因素的试验研究[J].振动、测试与诊断,2008,28(1):14-17.
[3]Miyaguchi K.Recent technical trends in NSK Technical.Tournal.Motion[J].Ninomiya M.ball screws Control.1998(664):1-13.
[4]康献民,王大承,王天雷.精密丝杠副中滚珠冲击及其影响因素研究[J].五邑大学学报(自然科学版),2009,23(4):1-6.
[5]康献民,王大承,李霆.基于爬行理论的滚珠丝杆进给系统加工波纹度成因的研究[J].组合机床与自动化加工技术,2010(8):16-19,23.
[6]德长靖,五十岚昭南,桥爪一宏.Studies on the sound and vibration of a ba11 screw(3th report.sound.caused by waviness on flank of screw shaft)[J] .Transactions of the Japan Society of Mechanical Engineers.1991(Part C):1874-1879.
[7] GALLINA P.Vibration in screw jack mechanisms: ex⁃perimental results [J] .Journal of Sound and Vibra⁃tion,2005,282(3):1025-1041.

