一种基于A*算法改进的最短路径搜索方法
,,
(1.上海电力学院 计算机科学与技术学院,上海 200090;2.中国计量大学 机电工程学院,浙江 杭州 310018)
城市交通导航中最基本的路线搜索就是最短路径问题,因此,我们经常会使用经典的广度优先算法——Dijkstra算法来解决该问题。其主要特点是以找寻的起始点开始搜索所有与其连接的点,从中心向外层扩展,直到找到终点。该算法大多用来计算单源最短路径。
另外一种常用的经典深度优先算法是Floyd算法。该算法利用动态规划的思想,通过加权寻找与距离起始点最短距离的点并深入下去,多用于计算多源最短路径。
虽然这两个算法都能解决最短路径的计算问题,但都存在着效率问题,不仅需要搜索大量的节点,而且如果遇上交通导航或者游戏寻路导航这样庞大的系统问题时,其处理能力和数据的存储还存在一定的局限。
A*算法作为另外一种算法,解决了庞大系统的计算和障碍物复杂度等问题,常被运用到城市交通和游戏的路径导航。因此本文着重于A*算法变种的对比和改进。
1 A*算法及其变种
1.1 A*基本算法
A*算法是目前广泛使用的基于启发式的最短路径算法,通过计算函数的相对最优解来筛选出发点周围的后继点,能适用于各种场景,相当灵活。它主要使用了静态路网中求解路径最有效的直接搜索方法——启发式,而且A*算法还使用了两个存放等待检查点的Open表和存放不需要再检查点的Close表,然后通过计算函数和父节点的对比来寻找路径上的点[1]。其计算函数公式如下
F(n)=G(n)+H(n)
(1)
式中:G(n)——从初始节点到任意节点n的代价;
H(n)——从节点n到目标点的预计消耗代价,也称启发式函数。
当点n对应的G(n)和H(n)为最小代价时,那么该点就作为最短路径中的临时点放入Close表中。
A*算法基本查找步骤如图1所示。图1中,起始点S的上下左右4个点都放入Open列表中,然后通过计算启发式找出最小的F值,该值所标识的后继点N即为接下来该走的点,然后将S点放入Close表中,并在N点上标注其父节点为S。图1中的G为设置的值,即上下左右节点距离父节点的距离都是10。
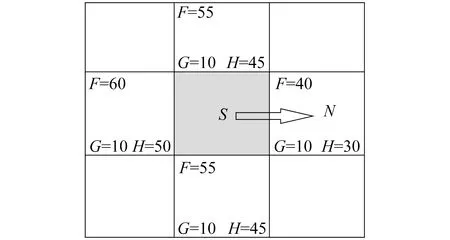
图1 A*算法基本查找步骤
启发式函数的作用是控制A*的行为。在不考虑极端的情况下,如果H(n)的值经常比从n移动到目标的实际代价小或者相等,则A*能保证找到一条最短路径。H(n)越小,A*扩展的节点越多,运行就越慢;如果H(n)精确地等于从n移动到目标的代价,则A*将会仅仅寻找最佳路径而不扩展别的任何节点,会使运行非常快。如果H(n)的值有时比从n移动到目标的实际代价大,则A*不能保证找到一条最短路径,但它运行得更快。
有很多启发式方程可以使用,不过本文测试使用的是最常见的曼哈顿距离来计算H(n)为
H(n)=D[|nx-gx|+|ny-gy|]
(2)
式中:nx,ny——点n当前的x轴和y轴坐标值;
gx,gy——目标点的x轴和y轴坐标值;
D——相邻位置的最小代价。
GHALLAB M等人[2]提出一种改进的A*算法。该算法临界值Fα(n)计算公式为
(3)
F(n)=cG(n)+dH(n)
(4)
c,d——定值权值。
Fα(n)选取的是从当前节点的动态F(n)值和父节点临界值之间比较下来的最大值。通过临界值的大小来筛选Fα(n)范围内的候选后继点,然后将其放入Open表中。这样做大大缩小了Open表的容量,减少了遍历搜索的时间,为之后搜索最佳后继点提供了便利。
编程时,在式(4)中添加了一个额外的AX集合放置符合Fα(n)范围内的点,如果AX为空,即找不到点,就缩小c和d的值以扩大后继点的范围,防止出现由于起点终点直线距离一直小于后继点的H(n)值而无法寻路的情况。
1.3 AlphaA*算法
该算法[3]的计算临界值公式为
Fα(n)=[1+W(n)]F(n)
(5)
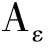
(6)
式中:H(s)——起点的启发式估算值。
当父节点的启发式估算值比起点的启发式估算值大的时候,就设置H(n)/H(s)的值为权值,动态控制范围。但是如果遇上起点终点直线距离小于实际应该走的路线的情况,就将权值设置为1,扩大搜索的范围,因此不存在找不到点的问题。AlphaA*算法更加稳定。
1.4 添加启发式算法
段莉琼等人[4]提出了一种改进启发式的算法,公式为
F(n)=G(n)+H(n)+H(n-1)
(7)
该算法添加的H(n-1)是计算当前节点的父节点到终点的最小代价。其优势在于可以马上去除偏离最短路径的点,使得搜索方向更加智能地趋向于终点。
2 改进算法A*+
综合上述算法,本文通过将添加启发式和静态加权的方式对A*算法进行了改进,即
F(n)=cG(n)+d[H(n)+H(n-1)]
(8)
(9)
通过式(9)设置Open表的临界值是为了减少排查后继点的时间。虽然是静态设置父节点为后继点提供的范围,但是依然可以动态地调整整个算法的权值,提高了计算最佳后继点的效率。
同时,在临界范围内添加一个查点判断条件:如果Open表中已经存在一个点,这个点又再次出现在当前点的周围,那么无论这个点的F(n)值是否在当前点的Fα(n)范围内,逻辑上都不可能成为最佳后继点,因此直接不考虑这个点。
While(flag){
求父节点的h值;
For(int i=0;i<方向数;i++){
当前点x轴坐标=父节点.x+x轴方向;
当前点y轴坐标= 父节点.y+y轴方向;
if (当前点在地图上为障碍物标记) {
continue;}
if(当前点超出了地图的范围){
continue; }
if(终点是当前点) {
终点.父亲 =父节点;
flag = false;
break;}
if(close表里已经存在当前点) {
continue;}
if(open表里存在当前点){ //将搜索重复的点删除,排除在范围外
NodeOpennode = getOpen(当前点);//从Open表里获取当前点
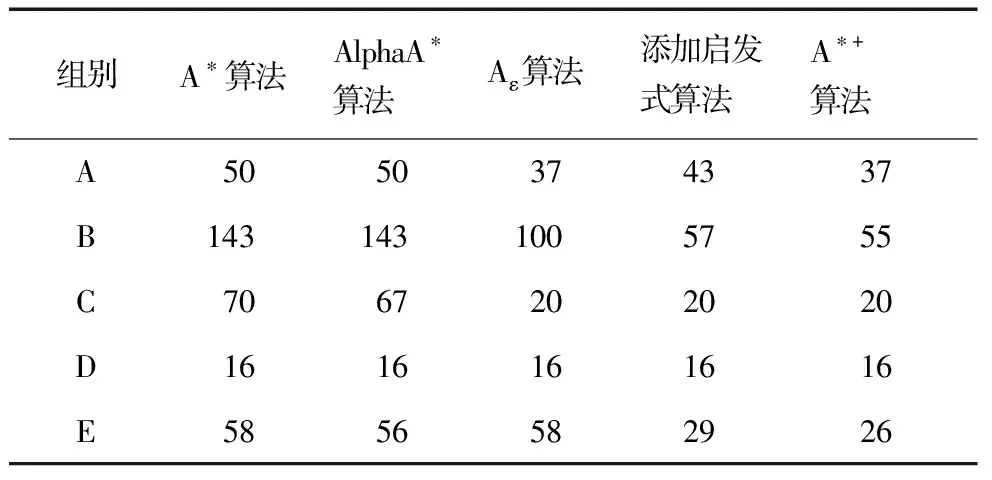
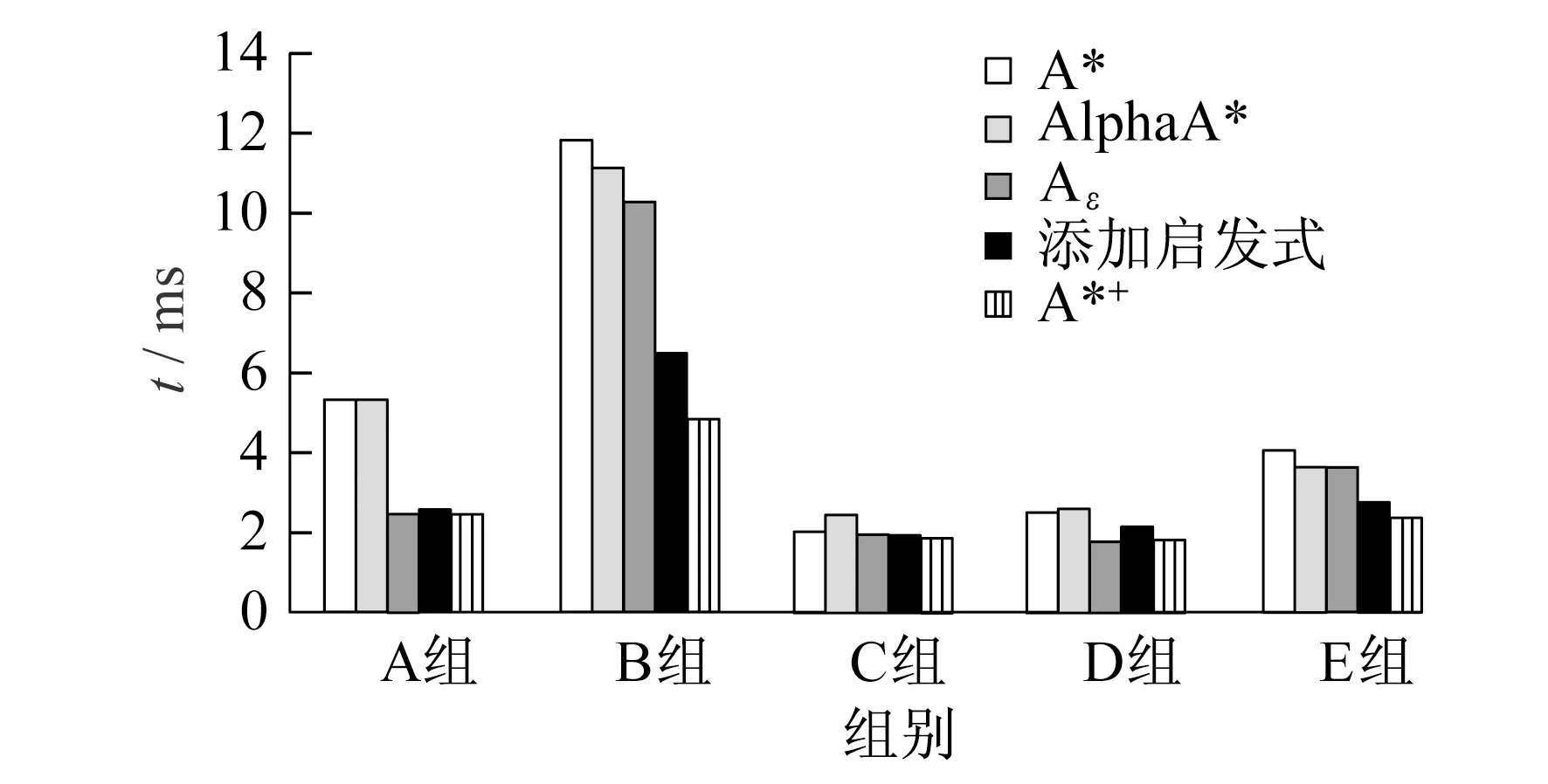
if(父节点.G + 10 Opennode.parent = 父节点; Opennode.G =父节点.G +代价值; Opennode.F=Opennode.G+Opennode.H+父节点的h;} if(Opennode.F OpenList.remove(Opennode);} continue;} else { Nodenownode = 该点; nownode.父亲 =父节点; nownode.G =父节点.G +代价值; nownode.H =该点到终点的代价估算; nownode.F = nownode.G +nownode.H+父节点的h; if(nownode.F<=threshold(父节点.F)){ OpenList.add(node2);} else continue;} } if(flag==false){ break;} 父节点 = Open表里f值最小的点; OpenList.remove(node); 将该父节点放入close表中;} 通过以上改进,该算法不仅减少了排查节点数,提高了效率,而且无论什么情况都可以找到后继点。 为了排除算法中其他部分的影响,使用ArrayList的数据结构来存放Open列表和Close列表数据,并以最常见的曼哈顿距离来计算启发式函数。由于算法多用于交通/游戏导航,地图方面障碍物必不可少,再加上A*算法通过地图网格化的数据来计算,因此用二维数组来作为本次实验的地图,设置的查找方向为上下左右。 测试5种不同情况下的算法表现,如图2所示。 A组表示起点终点直线距离比实际路线短很多的情况,即点(5,8)至点(3,14),见图2(a);B组表示起点终点直线距离远的情况,即点(4,16)至点(20,8),见图2(b);C组表示普通路线,即点(5,14)至点(18,7),见图2(c);D组表示起点终点间没有障碍物的情况,即点(3,6)至点(14,11),见图2(d);E组表示绕过障碍的情况,即点(5,8)至点(12,12),见图2(e)。 图2 5种不同情况下的算法表现 通过量化数据求取每组Close表和Open表中的节点个数,分别测试不同算法的节点搜索能力和筛选周围点的能力。Close表节点数比较见表1,Open表节点数比较见表2。 表1 Close表节点数 表2 Open表节点数 通过算法所用时间计算平均效率,判别算法的优化度,5种不同情况下算法的所用时间见图3。 图3 5种不同情况下算法的所用时间 本文主要研究了A*算法变种不同搜索排查能力所导致的效率问题。首先对这些算法的搜索能力和排查能力进行了分析对比,并对这些变种进一步分析改进。实验证明:本文提出的A*+算法大幅缩小了排查节点的范围,提高了计算效率和寻路过程中的方向性,使得找点更趋向于终点,且能很好地处理复杂的平面地形,距离越远,该算法的优势越突出。A*+算法应用广泛,不仅能更好地适用于城市交通导航和游戏人物导航,也适用于人工智能。 参考文献: [1] PATEL A.Amit’s A*pages[EB/OL].[2016-10-30].http://theory.stanford.edu/~amitp/GameProgramming/. [3] REESE B.AlphaA*:an ε-admissible heuristic search algorithm[R/OL].(1999-12-08)[2016-10-30].http://home1.stofanet.dk/breese/papers.html. [4] 段莉琼,朱建军,王庆社,等.改进的最短路径搜索A*算法的高效实现[J].海洋测绘,2014,24(5):20-22.3 实验对比分析
3.1 实验分组
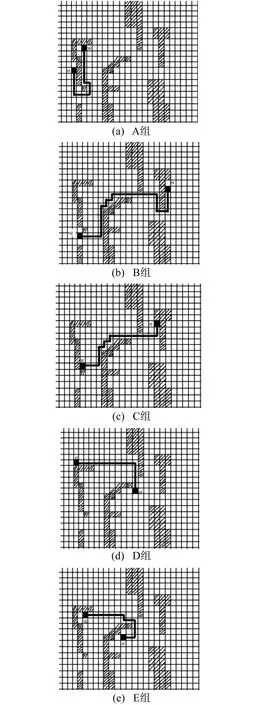
3.2 分 析

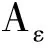
4 结 语