风电塔筒屈曲承载能力提高方法研究

文 | 李剑波，李学旺，黄冬明

塔筒是风力发电机组重要的支撑部件，不仅承受着叶片、机舱、塔筒的重量，还承受着风轮旋转产生的交变载荷以及风载荷，其强度决定了整机的安全性。钢制塔筒的强度计算主要包括静强度、疲劳以及屈曲，而塔筒的安全性通常由疲劳或屈曲决定；发生屈曲时，塔筒本身的最大应力没有达到材料的屈服强度，即屈曲先于静强度破坏而发生，因此屈曲承载能力计算对于塔筒强度计算来说非常重要。

塔筒的承载能力与经济性是难以破解的一对矛盾，增大塔筒壁厚无疑可以提高塔筒的屈曲承载能力，但增大壁厚会导致塔筒重量急剧增加，经济性较差。那么如何提高塔筒的屈曲承载能力而又经济可行十分值得研究。本文将从理论和有限元分析两个方面来研究风力发电机组塔筒屈曲承载能力的提高方法。

塔筒稳定性理论分析

塔架结构属于细长杆，可以从材料力学的角度用欧拉理论来分析其可以承受的最大临界载荷。工程实际中，通常采用DIN标准对塔架屈曲承载的安全性进行计算。下面将分别从欧拉理论和DIN屈曲计算方法两个方面来研究塔架屈曲承载能力提高方法。

一、欧拉临界载荷

根据材料力学的知识可知，塔架可以简化为一端固定一端自由的细长杆。其欧拉临界压力为：

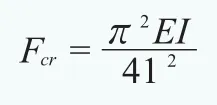
Fcr——欧拉临界压力、E——材料弹性模量、I——截面惯性矩、l——杆件长度

根据欧拉公式可知，塔架的屈曲承载能力与高度成反比，与弹性模量和截面惯性矩成正比。对于一款机组来说，其塔架高度l通常是固定的。而各种钢材的弹性模量E大致相等，所以选择优质钢材或者是低碳钢并无很大差别。因此决定塔架屈曲稳定性的主要因素是塔架的截面惯性矩I，而截面惯性矩由截面形状决定。锥形钢制塔筒的截面形状为圆环，增大塔筒的直径和壁厚都可以提高截面惯性矩，从而提高塔架屈曲承载能力，但是这一方法会明显提升塔架的成本，降低经济性。

二、DIN屈曲计算方法

DIN18800-4标准中给出了常量壁厚的柱形壳体的屈曲计算方法以及常量壁厚的锥形壳体的屈曲计算方法。实际中，塔筒为不同壁厚的钢板焊接而成的锥形壳体。校核变壁厚的锥形塔筒需要把塔筒分为多个等壁厚的小段，把这些小段转化为与所在塔段等长的长圆锥，再把长圆锥转化为圆柱。 DIN18800-4屈曲计算标准中考虑了轴向应力、剪切应力和环箍应力三个分量对屈曲承载能力的综合作用。其中轴向应力起决定作用，剪应力起次要作用，环箍应力的影响很小。为了简化分析流程，本文主要考虑轴向应力分量对屈曲承载的影响。

轴向许用翘曲应力等于实际翘曲应力除以材料安全系数，按式（1）计算：

式中：σxSRd——轴向许用翘曲应力；σxSRk——轴向实际翘曲应力；γM——材料安全系数

实际翘曲应力等于特征屈服应力乘以缩减系数：

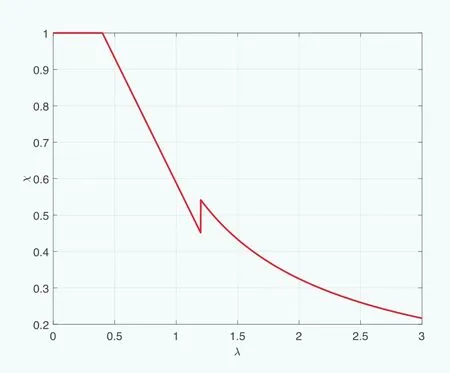
图1 缩减系数与细长度的关系图

式中： χ——缩减系数；fyk——特征屈服应力

而缩减系数又是细长度的函数，对于正常缺陷敏感度的外壳，其关系如图1所示，横轴为细长度，纵轴为缩减系数。

非量纲细长度λsx按式（3）计算：

式中：λsx——非量纲细长度；σxsi——轴向压缩下圆柱的理想翘曲应力

轴向压缩下圆柱的理想翘曲应力σxsi按式（4）计算：

式中：Cx——由长度决定的系数；t——塔筒壁厚；r——塔筒半径

系数Cx根据外壳的长度确定。对于轴向屈曲，满足下式时属于长圆柱。塔筒一般分为四节，按照DIN标准，各个小节基本上都属于长圆柱。

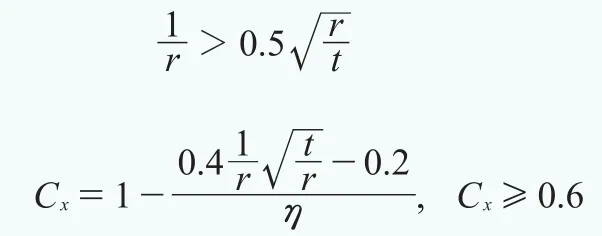
η根据支撑条件确定，取1或3（底段）。

由上述计算过程可知，提高材料强度在一定程度上可以提高屈曲承载极限，但是材料强度提高会导致缩减系数 χ减小，而缩减系数减小会使实际翘曲应力减小。为了定量分析材料强度对屈曲承载力的影响，取一节长15m，外径4m，壁厚0.03m的等壁厚长圆柱塔筒进行计算对比。分别计算材料为Q345和Q390的两种筒段的实际翘曲承载力。

由计算结果可知，提高材料强度对屈曲承载力影响较小，而且选用高强度的材料会导致焊接性能下降，进而影响塔筒焊缝的疲劳强度；另外高强度的材料对缺陷更加敏感，也会影响塔筒的屈曲承载能力。

塔筒稳定性提高有限元分析

屈曲分析也叫稳定性分析，就是求解结构从稳定平衡过渡到不稳定平衡的临界载荷。采用有限元方法对结构进行屈曲分析时，一般有特征值屈曲分析和非线性屈曲分析两种方法。特征值屈曲用于预测一个理想弹性结构的理论屈曲强度，这种方法计算简便高效；非线性屈曲分析比特征值屈曲分析更加精确，但是有费时和计算量大等缺点。本文采用特征值屈曲分析方法研究加纵筋和横向环筋对塔筒屈曲承载力的影响。取一节长15m，外径4m，壁厚0.03m的塔筒，采用实体单元进行屈曲分析。分别研究加横向环筋和纵筋对屈曲承载力的影响。

一、横向环筋对屈曲承载力的影响

分别计算不加筋，加一个环筋，加两个环筋的塔筒的屈曲承载能力。加一个环筋的模型中环筋加在塔筒中间部位，加两个环筋的模型中每隔五米加一个，均匀分布；同理，加三个环筋和四个环筋均按均匀分布。加环筋的塔筒几何模型如图2－图5所示。约束模型底部所有自由度，顶部加载弯矩Mx＝1e7kNm。

图2 塔筒加一个横向环筋的几何模型

图3 塔筒加两个横向环筋的几何模型

图4 塔筒加三个横向环筋的几何模型

图5 塔筒加四个横向环筋的几何模型

表1 不同材料的实际翘曲承载力计算表

塔筒特征值屈曲分析的屈曲波形如图6－图10所示。

塔筒加环筋特征值屈曲分析计算得到的载荷因子如表2所示。从表中可知，加一个环筋时相对于不加筋载荷因子仅仅提高了0.38%，加两个环筋时相对于不加筋载荷因子提高了0.95%，加三个环筋时相对于不加筋载荷因子提高了5.5%，加四个环筋时相对于不加筋提高了7.1%。由此可见，加一个或两个环筋对塔筒屈曲承载能力的提高影响较小，而加三个或四个环筋对塔筒的屈曲承载有一定的提高；然而增加三个或者四个环筋时会导致塔筒重量急剧增加，更多的焊接也会带来更大的焊接变形，制造精度难以保证。因此，通过增加环筋的方式来提高塔筒的屈曲承载能力不具可行性。

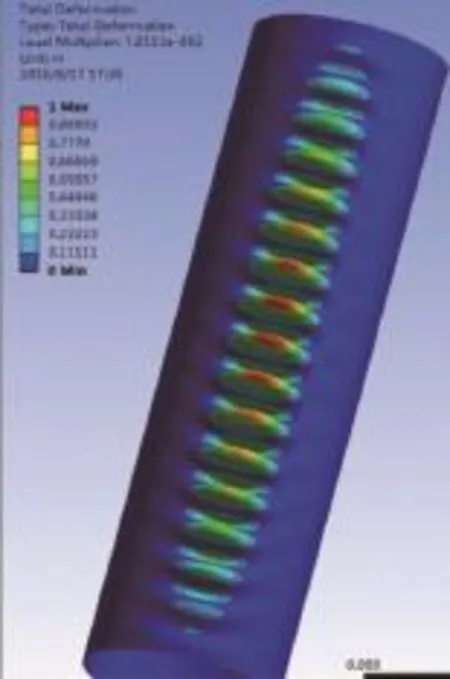
图6 不加环筋时塔筒屈曲变形结果

图7 加一个环筋时塔筒屈曲变形结果

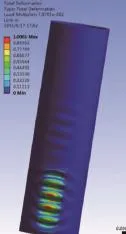
图8 加两个环筋时塔筒屈曲变形结果

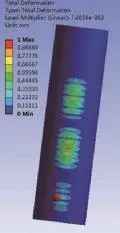
图9 加三个环筋时塔筒屈曲变形结果

图10 加四个环筋时塔筒屈曲变形结果

图11 塔筒加一根纵筋几何模型

图12 塔筒加两根纵筋几何模型

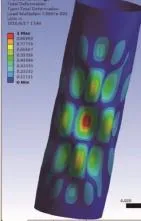
图13 加一根纵筋（受压）塔筒屈曲变形

图14 加两根筋塔筒屈曲变形图

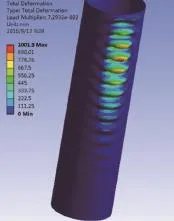
图15 加一根纵筋且纵筋受拉塔筒屈曲变形图

二、纵筋对屈曲承载力的影响

为了研究加纵筋对塔筒屈曲承载能力的影响，分别计算塔筒加一根纵筋和两根纵筋的屈曲承载能力，同时研究加载方向对屈曲承载的影响。加筋的几何模型如图11－图12所示。塔筒加纵筋载荷因子计算结果如表3所示。屈曲变形结果如图13－图15所示。从表3载荷因子计算结果可知，塔筒加一根纵筋且使纵筋受压时塔筒屈曲承载能力提高了14%，加一根纵筋且使纵筋受拉时屈曲承载能力提高了4%，加两根纵筋时屈曲承载提高了17.67%。由此可见，加两根纵筋时对于提高塔筒的屈曲承载能力十分有效，而若再增加纵筋数量，一方面会导致塔筒重量的增加，降低经济性；另一方面再增加纵筋需要更多的焊接工装，同时会造成更大的焊接变形，难以保证塔筒的制造精度。

表2 塔筒加环筋载荷因子计算结果

表3 塔筒加纵筋载荷因子计算结果

摄影：车传江

结论

本文从理论分析和有限元仿真两个方面对提高塔筒屈曲承载能力的方法进行了研究。欧拉理论分析表明，提高塔筒截面惯性矩可以有效提高塔筒的屈曲承载能力；DIN屈曲计算方法研究表明，钢材的强度对塔筒屈曲承载能力影响较小；有限元分析结果表明，加一个或两个环筋对塔筒屈曲承载能力的提高影响较小，加三个或四个环筋对塔筒的屈曲承载有一定的提高，然而增加三个或者四个环筋时会导致塔筒重量急剧增加，更多的焊接也会带来更大的焊接变形，制造精度难以保证。因此，通过增加环筋的方式来提高塔筒的屈曲承载能力不具可行性；而加两根纵筋就可以明显地提高塔筒的屈曲承载能力，具有实际可行性。本文研究结果对于经济可行地提高塔筒的屈曲承载能力提供了参考。