结合最大似然算法和波利亚罐模型的全色遥感图像分类

李 杰，李 玉，王 玉，赵泉华

(辽宁工程技术大学测绘与地理科学学院遥感技术与应用研究所，辽宁 阜新 123000)

图像分类是根据图像中像素的一些特殊性质(如光谱测度、空间结构特征等)，按照某种规则或算法将图像分成具有一致特性区域的方法和手段[1]。目前，根据是否使用类别的先验知识，图像分类方法可以分为监督和非监督两种方法。其中，监督分类方法最为引人注目。

监督分类是一种具有较高精度的统计判决分类方法，通过已知样本的类别和类别的先验知识，确定判别函数和相应的判别准则。根据函数和准则，把图像中的各个像素点归属到各个给定类，完成图像分类[2]。常用的监督分类方法为最大似然(maximum likelihood，ML)分类法[3]；非参数分类方法包括K最邻近分类算法(KNN)[4]、K均值算法(K-means)[5]、模糊分类法[6]、基于Fisher准则的分类方法[7]、SVM分类方法[8]、基于马尔可夫模型的分类方法[9]等。在这些方法中，ML算法是一种应用非常广泛的图像分类方法，且具有快速、简单、对大部分图像均可得到较为准确的分类结果等优点。

然而，ML算法作为一种监督分类方法，将样本区域像素的统计特征值作为类别的统计特征值来构建类别的判别函数，因此样本区域选择是否科学合理直接关系到判别函数的正确性和最后分类的精度。另外，ML算法以像素为处理单元实现分类，没有考虑邻域像素的作用，易使分类结果中产生误分像素，特别是在高分辨率遥感图像的分类中。为此，本文将ML算法和波利亚罐模型结合起来，提出一种改进上述问题的图像分类方法。

波利亚罐模型是Polya和Eggenberger[10]为模拟传染病在人群中的扩散而提出的一种随机试验模型。该模型试验对罐中不同颜色的小球进行随机抽取，每次取出一个小球，记录颜色后放回，然后加入一些相同颜色的小球，以这个过程模拟传染病的扩散。该过程每进行一次，罐中小球的组成会发生变化，随着抽取次数的增加，被抽到次数最多的某种颜色的小球在罐中的数量会逐渐增多。根据这种随着抽取次数增加，某颜色小球数量逐渐增多的现象，为波利亚罐模型提出“时间传染”的特性。在该模型的应用中，Alajaji等[11]提出一种能够去除噪声的图像重建方法；耿茵茵等[12]提出一种区分图像前景和背景的判决机制，并应用于指纹图像的处理中；Banerjee等[13]则把该模型与图像像素的邻域相结合，提出“空间传染”的特性，并与Polya等提出的“时间传染”特性一同应用到图像分类中，有效提高了图像的分类精度，但在处理纹理特征变化较大的区域上依然存在问题。

本文在Banerjee等提出的理论基础上，将ML算法和波利亚罐模型结合起来，完成高分辨率全色遥感图像的分类。通过对合成图像与真实遥感图像的分类试验，验证本文方法的可行性和有效性。

1 算法描述

1.1 波利亚罐模型

罐模型是一种随机试验模型，根据预先设计的方案，对罐中不同颜色的小球进行抽取，并根据取到的小球颜色改变罐中各种颜色小球的数量，从而改变罐中各种颜色小球的组成[14]。罐模型中包含许多重要的概率分布，在概率论和应用概率中有十分重要的地位[15]。

波利亚罐模型是一种重要的罐模型。设罐中有B个蓝色小球和W个白色小球，从中随机抽取一只，记录颜色后放回，并加入c个相同颜色的小球。每次抽取后，取出的某颜色小球(如蓝色小球)数量增加，而另一种颜色小球(如白色小球)数量不变。反复进行上述过程，直到满足预设的终止条件，这种随机试验模型称为波利亚罐模型。以下是该模型的一些基本性质和推论。

性质：以Xn表示前n次抽取中取到蓝色小球的次数，P(Xn=k)表示这n次抽取中取到蓝色小球次数为k的概率，P(Xn=k)可表示为

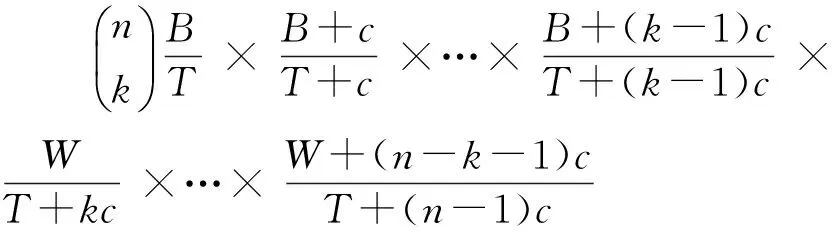
(1)

式中，T=B+W，表示进行抽取前罐中蓝、白两种颜色小球的总个数。式(1)分子分母同除以c，并令α=B/c，β=W/c，T/c=α+β，得到式(2)的另一种表达方式，即

α(α+1)…(α+(k-1))×β(β+1)…(β+(n-k-1))=

(2)

式中，〈α〉k=α(α+1)…(α+(k-1))；〈β〉n-k=β(β+1)…(β+(n-k-1))；〈α+β〉n=(α+β)(α+β+1)…(α+β+(n-1))。

推论：根据式(2)可得n次抽取过程中，取到蓝色小球次数的期望E(Xn)

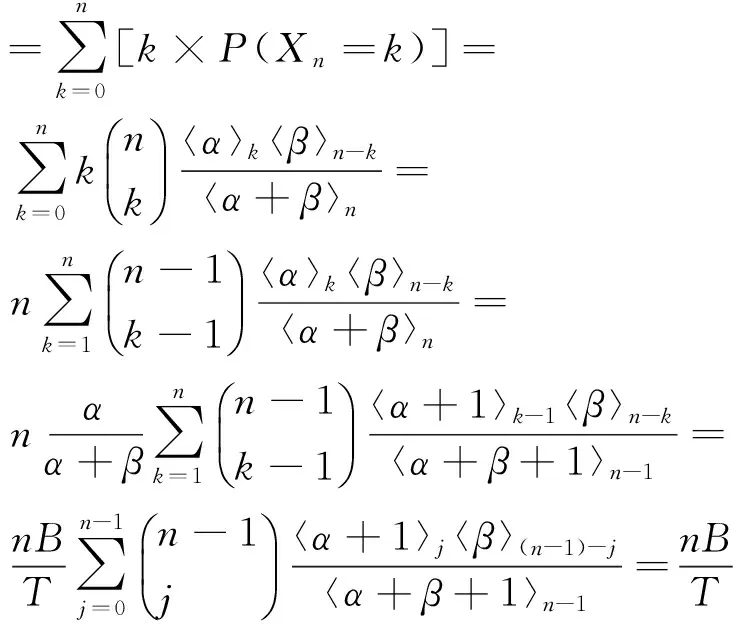
(3)

设Yn表示n次抽取后罐中蓝色小球的总个数，则Yn=cXn+B，E(Yn)表示n次抽取后罐中蓝色小球总个数的期望，由Yn及E(Xn)可得

(4)

可得出n次抽取后罐中蓝色小球所占比例为

(5)

式(5)表明，n次抽取后罐中蓝色小球数与小球总数比等于最开始时罐中蓝色小球数与小球总数之比。因此，若抽取前罐中某颜色(类别)小球数量占优，经过若干次抽取后，该颜色(类别)小球仍然占优。该推论体现波利亚罐模型具有保持罐中小球主要类别的特点，也说明了文献[10]中“时间传染”的特性。将该推论运用到图像分类中，可以用来增强像素的归属概率最大的那一类别。

为利用波利亚罐模型实现图像分类，将图像中的各像素用一包含不同颜色小球的罐表示，小球的各类颜色对应图像的各个类别，像素属于各类别的概率对应各颜色小球的数量，像素归属某一类别的概率越大，则该类别(颜色)小球数量越多。本文提出方法首先对图像各类别进行随机采样，由ML算法计算单个像素属于各类别的概率，根据得到的概率计算该像素对应的罐中各类别小球的数量及占总球数的比例，按所得比例抽取小球。由取到小球的类别，增加该类别小球的数量，再重新计算各类别小球的数量及比例，并确定下一次各类别的抽取比例。以上过程模拟波利亚罐模型的抽取过程，可保持罐中小球的主要类别。将该过程运用到图像分类中，针对单个像素，可以增强其主要归属类别，若结合邻域，可将中心像素划分到更合适的类别中去，有效弥补ML算法易产生误分像素的缺点，提高图像的分类精度。

1.2 基于波利亚罐模型的图像分类

1.2.1 图像罐模型建立

1.2.1.1 图像数据结构

设I={p(i，j);i=1,2,…,a，j=1,2,…,b}表示一幅尺度为a×b的图像，其中(i，j)为像素在图像中的空间坐标，p为像素(i，j)的光谱测度。在利用波利亚罐模型的图像分类中，以罐u(i，j)表示像素(i，j)，为图像I建立罐模型U={u(i，j);i=1,2,…,a，j=1,2,…,b}，则

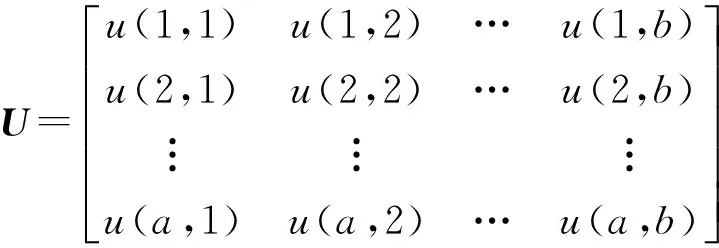
(6)

1.2.1.2 建立罐模型

用P(i，j)(l)表示像素(i，j)属于第l类的概率，l∈{1,2…,L}。根据ML算法，P(i，j)(l)可由式(7)计算得出

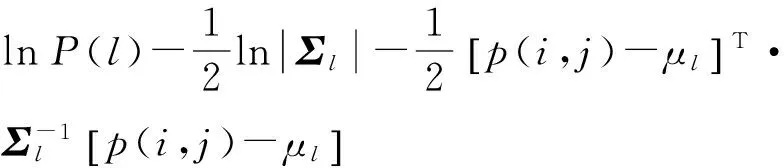
(7)

式中，μl和Σl分别为第l类样本区域的均值及协方差矩阵；P(l)为第l类的先验概率[16]。本文使用初次ML算法得到，其对数形式为

(8)

用P(i，j)(l)乘以罐中小球总数T(规定各罐中小球总数相同)，计算罐u(i，j)中类别为l的小球的数量，完成图像罐模型的建立。根据上述过程，对尺度为a×b且有L个目标类的图像建立罐模型，设Gl,0(i，j)表示进行0次抽取过程后，类别为l的小球数量，则Gl,0(i，j)为

Gl,0(i,j)=T×P(i,j)(l)

(9)

式(9)可将像素属于各类别的概率P(i，j)(l)转化为各类别小球的数量。则进行0次抽取过程后，像素(i，j)的罐模型为u0(i，j)={Gl,0(i，j)|l=1,2，…,L}，该过程如图1所示。

图1 像素(i，j)各类别概率P(i，j)(l)及其罐模型u0(i，j)

图1为分为3类(L=3)的图像建立罐模型的过程。若图中像素(i，j)属于各类别的概率分别为：P(i，j)(1)=0.6，P(i，j)(2)=0.1，P(i，j)(3)=0.3。令罐中黑、灰、白这3色分别对应1、2、3这3种类别，设T=10，则像素(i，j)的罐模型u0(i，j)中含6个黑色(1类)小球、1个灰色(2类)小球、3个白色(3类)小球，即G1,0(i，j)=6，G2,0(i，j)=1，G3,0(i，j)=3。将以上过程作用于图像中的其他像素，完成罐模型的建立。

u0(i，j)为像素(i，j)罐模型的初始表示方式，以此类推，则un-1(i，j)表示第n-1次抽取后，进行第n次抽取前像素(i，j)的罐模型，n=1,2,…。

1.2.2 结合邻域的分类过程

为避免仅根据单个像素进行分类导致结果出现误分的问题，需要充分利用图像像素的邻域信息。将波利亚罐模型抽取过程扩展到邻域中，考虑邻域像素对抽取结果的影响。首先为罐un-1(i，j)定义邻域，根据邻域中各个像素属于各类别的概率，计算此邻域中各类别小球的数量及占总球数的比例。按所占比例，使用赌轮盘随机选择算法[17]选取小球，由选中的结果更新un-1(i，j)中小球的组成，得到un(i，j)，并计算un(i，j)中各类别小球的数量及比例。根据新得到的比例，使用赌轮盘算法进行新一轮小球选取，并更新un(i，j)中小球的组成。上述过程重复进行，直到达到预定的抽取次数或各类别小球的数量所占比例趋于稳定。具体实现步骤如下：

1.2.2.1 超瓦罐模型

为罐un-1(i，j)定义邻域，将该邻域中所有罐模型集中起来，形成的集合称为un-1(i，j)的超瓦罐模型，以Sn-1(i，j)表示，则

Sn-1(i,j)={un-1(r,s)|(r,s)∈Nd,n=1,2,…}=

{Gl,n-1(r,s)|(r,s)∈Nd,l=1,2，…,L,n=1,2,…}

(10)

式中，Nd表示un-1(i，j)的邻域[18]，即

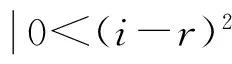
(11)

若d=2，则Sn-1(i，j)表示un-1(i，j)周围8个相邻罐的集合，如图2所示。其中，图2(a)中灰色部分表示像素(i，j)的3×3邻域，邻域像素各类别概率如图所示，结合前文，得到罐un-1(i，j)的超罐模型Sn-1(i，j)(如图2(b)所示)。

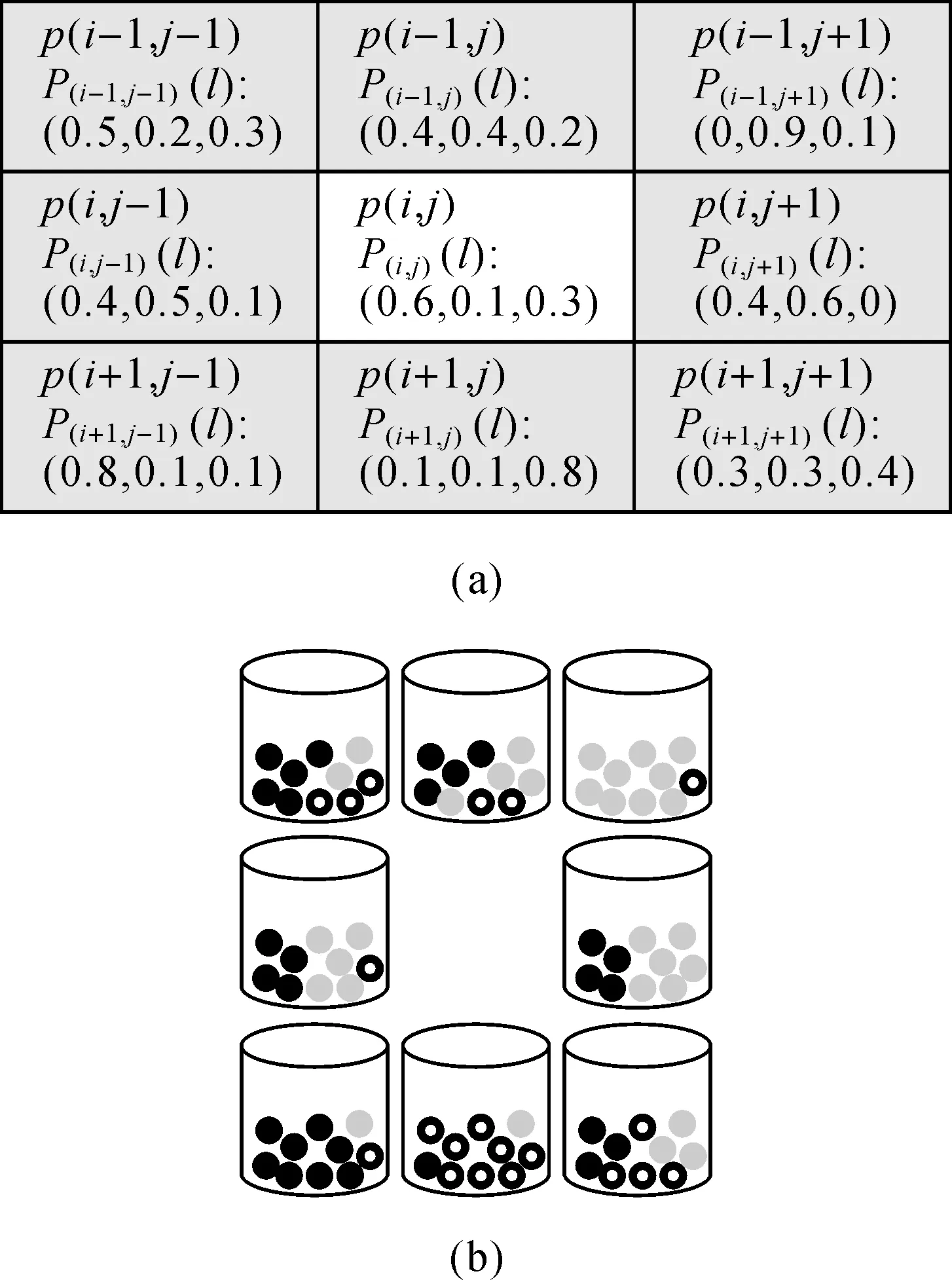
图2 像素(i，j)邻域及罐un-1(i，j)超瓦罐模型Sn-1(i，j)示意图

1.2.2.2 抽取及成分更新

根据图3方法在超瓦罐Sn-1(i，j)中模拟波利亚罐模型的抽取过程。

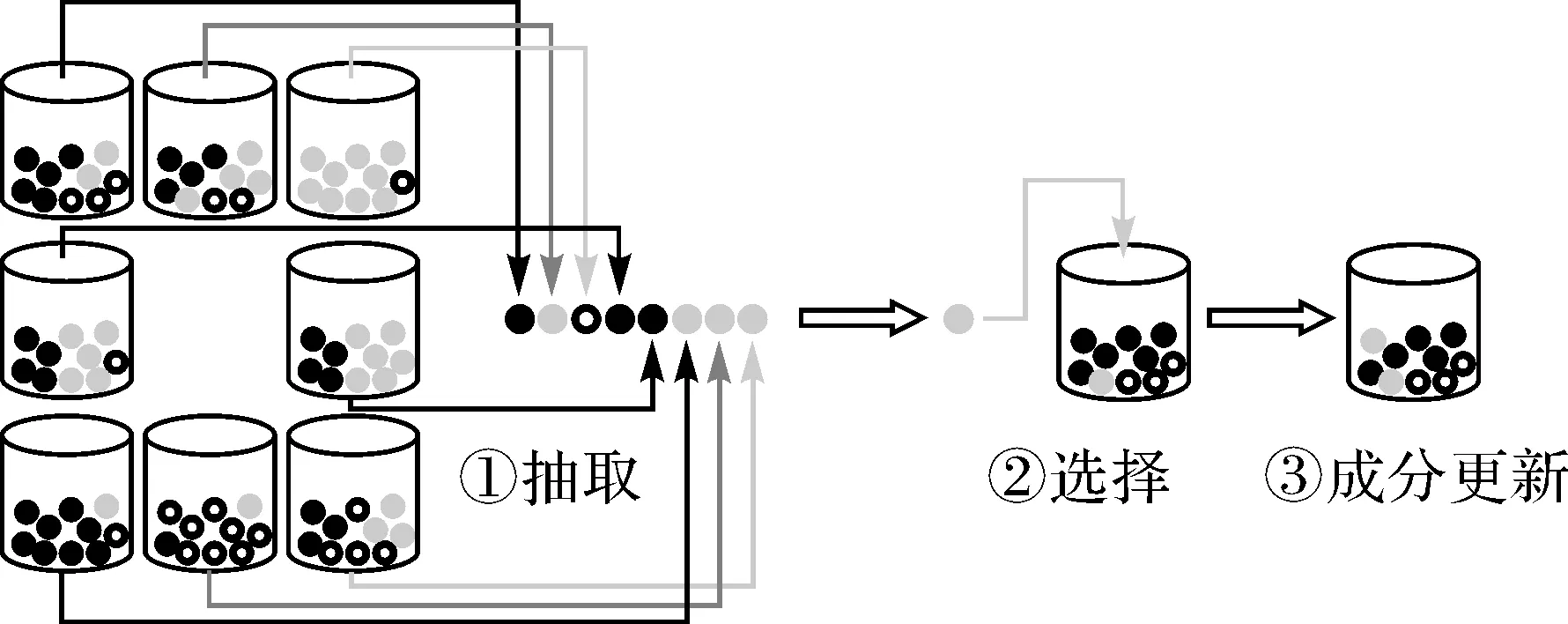
图3 抽取及成分更新过程

图3中，在Sn-1(i，j)中的8个罐模型的中使用赌轮盘随机选择方法各取出一个小球，共得到8个小球，假定得到小球的颜色分别为：黑、灰、白、黑、黑、灰、灰、灰(①)，此次抽取得到的灰色(2类)小球个数最多(②)，则向un-1(i，j)中加入c个灰色(2类)小球(③，此图中c=1)，得到成分更新后的罐模型un(i，j)。若①中抽取结果出现颜色不同数量相同的情况，则任意选取其中一种颜色(如出现3黑3灰2白或4黑4灰0白，则在黑色和灰色中任选一色)。②中得到的颜色(类别)用Jn(i，j)表示，则Jn(i，j)=2。

针对分为L类的图像，Jn(i，j)取值如下

Jn(i,j)=ll=1,2，…,L

(12)

式(13)表示第n次抽取的结果中，颜色(类别)最多的小球为l类小球，则向罐un-1(i，j)中加入c个l类小球，得到罐un(i，j)，该过程可表示如下

un(i,j)={Gl,n(i,j),Gl′,n(i,j)|l,

l′=1,2，…,L,l≠l′,n=1,2,…}

(13)

式(14)中，如果Jn(i，j)=l，则Gl,n(i，j)=Gl,n-1(i，j)+c，Gl′,n(i，j)=Gl′,n-1(i，j)。

以上过程重复进行，若罐un-1(i，j)中各颜色小球数量比与罐un(i，j)中对应颜色小球数量比基本一致，停止抽取，此时图像分类结果达到稳定。假设总共进行了H次抽取，则uH(i，j)={Gl,H(i，j)|l=1,2，…,L，H=1,2,…}，若

(14)

则像素(i，j)归属于类别M，分类完成。

以上过程模拟波利亚罐模型的随机试验过程，结合像素邻域，可将中心像素划分到更合适的类别中去，利用波利亚罐模型保持罐中小球主要类别的特性，可以强调像素合适的类别，有效避免误分，使图像分类结果更准确。

1.3 方法流程

本文结合最大似然算法和波利亚罐模型进行图像分类，方法流程总结如下：

(1) 由最大似然算法，得到像素(i，j)属于各类别的概率P(i，j)(l)。

(2) 根据P(i，j)(l)，为像素(i，j)建立罐模型。

(3) 定义邻域Nd,根据Nd建立超瓦罐模型。

(4) 在超瓦罐模型中进行波利亚罐模型的抽取过程，更新罐模型。

(5) 步骤(3)、(4)重复进行，直至达到预定的抽取次数或罐模型中各颜色小球数量比趋于稳定，得到最终分类结果。

2 试验结果和讨论

采用本文方法分别对合成全色遥感图像和真实全色遥感图像进行分类试验，与ML算法、文献[13]算法的分类结果进行对比，并对试验结果进行定性和定量分析。

2.1 合成图像分类

为了准确对分类方法进行定性、定量评价和比较，对尺度为128×128像素的合成图像进行分类试验。合成图像以图4(a)为模板图像，并从0.5 m分辨率Worldview-2全色遥感图像中截取不同地物目标填充到模板图像上，其中，①—⑤区域依次为树林、农田、海水、人工建筑、裸地。图4(b)为生成的合成图像。

图4 模板图像和合成图像

利用ML算法对图4(b)进行试验，在图4(b)不同位置上对各类别进行样本选取， 所选取的4组样本在原图中位置如图5(a1)—(d1)所示。结果如图5(a2)—(d4)所示，其中图5(a2)—(d2)、(a3)—(d3)、(a4)—(d4)分别为ML算法、本文方法、文献[13]算法、ML和概率松弛算法的试验结果。

由图5(a2)—(d2)可以看出，ML算法对图像中纹理特征变化较大的区域(如①、②区域)分类效果很差，需要对此进行改进。本文方法采用像素5×5邻域(d=8)作为超瓦罐模型，取T=100，c=10，得到的最终分类结果如图5(a3)—(d3)所示。可以看出本文方法分类结果比较理想，对比图5(a2)—(d2)各区域的误分像素明显减少，能够有效保持各类别的边缘，得到较为可靠的试验结果，一定程度上解决了ML算法中的问题。且4组试验结果相近，说明样本对本文方法基本没有影响。

图5(a4)—(d4)为文献[13]算法的分类结果，该文献同样使用波利亚罐模型实现图像分类。文献[13]算法采用像素的3×3邻域定义Sn-1(i，j)，从Sn-1(i，j)中直接进行抽取，没有考虑Sn-1(i，j)中各un-1(r，s)的成分组成，使得抽取和选择过程过于简略，且使用的邻域过小，利用不到更多的邻域像素，试验结果并不理想。

为了对试验结果进行定量精度评价，以模板图像图4(a)为参考图像，分别得出ML算法、本文方法、文献[13]试验结果的混淆矩阵，并据此计算总体精度及Kappa值，计算结果列于表1。比较表1中4种方法的总体精度和Kappa系数，可以看出使用本文方法进行图像分类得到较好的结果。4组试验总体精度和Kappa系数都在0.99左右，均高于ML算法、文献[13]算法的a、b、c组试验。虽然在d组试验中本文方法Kappa系数略低于ML和概率松弛算法，但本文方法分类精度远高于优质分类器(Kappa系数0.8)标准[19]，且仅相差5.5×10-3，对分类精度的影响可忽略。

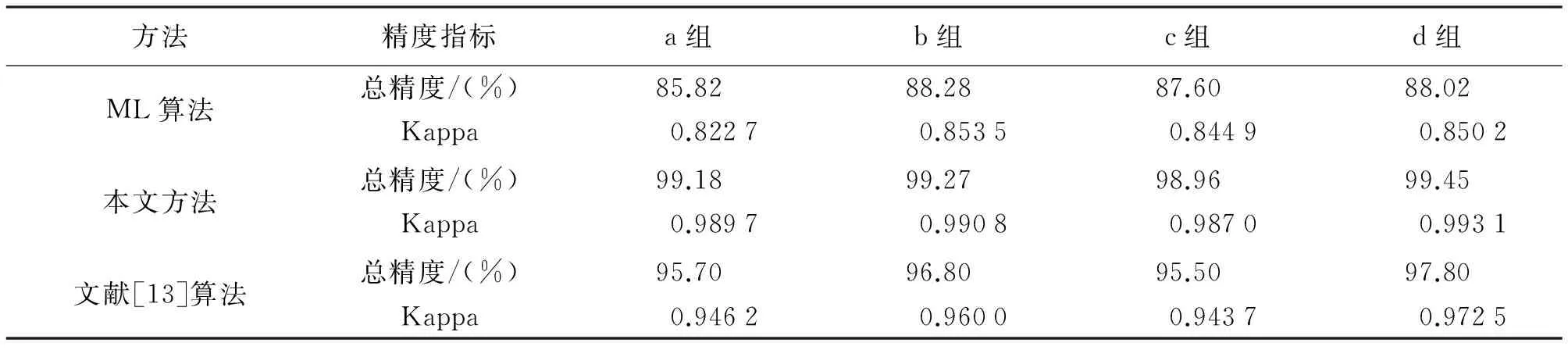
表1 图5(a2)—(d4)总精度和Kappa系数

2.2 真实遥感图像分类

为验证本文方法的适用性，选取2幅类数为4、尺度为256×256像素的1 m分辨率IKONOS全色遥感图像(如图6所示)进行分类试验。每幅图像随机选取4组样本(如图7(a1)—(d1)、图8(a1)—(d1)所示)，分别使用ML算法、本文方法及文献[13]算法进行处理，并对试验结果进行对比分析。

图6 IKONOS图像

图7(a2)—(d2)、图8(a2)—(d2)为ML算法试验结果，可以看出结果不够理想。如图7(a2)—(d2)树林类(图6(a)①区域)、图8(a2)—(d2)两类沙地(图6(b)③④区域)被分成2类或3类，其他区域也包含大量误分像素。图7(a3)—(d3)、图8(a3)—(d3)为本文方法试验结果，使用像素5×5邻域定义Sn-1(i，j)得到的最终分类结果。从整体上看，该结果中误分像素明显减少，既能够将不同类型地物区分开，又保持了各地物的形状。图7(a3)—(d3)4组试验、图8(a3)—(d3)4组试验彼此结果相近，可以说明样本对本文方法基本没有影响。图7(a4)—(d4)、图8(a4)—(d4)为文献[13]算法试验结果，对比本文方法，文献[13]算法分类结果不佳，且不能有效保持各地物形状。

根据真实遥感图像的试验结果，说明本文方法在一定程度上优于另外3种方法，有效对各地物的分类进行了改进，使结果更加准确。

3 结 语

本文提出一种结合最大似然算法和波利亚罐模型进行图像分类的方法，该方法可以有效改进最大似然算法的一些缺点。首先根据ML算法为图像建立罐模型，利用波利亚罐模型两个传染特性，可以使像素的主要归属类别得到增强。在此基础上考虑像素与其邻域间的关系，可以消除各类别中孤立的误分像素，提高图像的分类精度。试验结果表明，本文方法能够有效对高分辨率全色遥感图像进行分类，并具有较高的准确率。通过4组随机采样的试验结果，可以看出本文方法基本不受样本区域的影响，避免了ML算法对样本质量要求精确的缺点，有效简化了图像分类过程。

图8 图6(b)试验结果

参考文献：

[1] 梅安新，彭望琭，秦其明.遥感导论[M].北京：高等教育出版社，2001：193.

[2] 孙家抦.遥感原理与应用[M].2版.武汉：武汉大学出版社，2009：204-206.

[3] KELLY P A，DERIN H，HARTT K D.Adaptive Segment-ation of Speckled Images Using a Hierarchical Random Field Model[J].IEEE Transactions on Acoustics，Speech，Signal Processing，1988，36(10)：1628-1641.

[4] AITKENHEAD M J，Aalders I H.Classification of Landsat Thematic Mapper Imagery for Land Cover Using Neural Networks[J].International Journal of Remote Sensing，2008，29(7)：4129-4150.

[5] 周鲜成，申群太，王俊年.基于微粒群的K均值聚类算法在图像分类中的应用[J].小型微型计算机系统，2008，29(2)：333-336.

[6] 任明艺，李晓峰，李在铭.一种基于模糊分类的运动目标检测算法[J].信号处理，2012，41(4)：435-438.

[7] 辛芳芳，焦李成，王桂婷.非局部均值加权的动态模糊Fisher分类器的遥感图像变化检测[J].测绘学报，2012，41(4)：584-590.

[8] 谭熊，余旭初，秦进春.高光谱影像的多核SVM分类[J].仪器仪表学报，2014，35(2)：405-411.

[9] 刘梦玲，何楚，苏鑫.基于pLSA和Topo-MRF模型的SAR图像分类算法研究[J].武汉大学学报(信息科学版)，2011，36(1)：122-125.

[10] EGGENBERGER F，POLYA G.Uber Die Statistik Verketter Vorgange[J].Zeit Angew Math Mech，1923，3(4)：279-289.

[11] ALAJAJI F，BURLINA P.Image Modeling and Restoration Through Contagion Urn Schemes[C]∥International Conference on Image Processing.Washington，D.C.：IEEE Computer Society Press，1995.

[12] 耿茵茵，蔡安妮，孙景鳌.基于瓦罐模型的多判据判决及其在图像分割中的应用[J].电子学报，2002，30(7)：1017-1019.

[13] BANERJEE A，BURLINA P，ALAJAJI F.Image Segmentation and Labeling Using the Polya Urn Model[J].IEEE Transactions on Image Processing，1999，8(9)：1243-1253.

[14] MAHMOUD M H.Polya Urn Models[M].Boca Raton，State of Florida：CRC Press，2009：50-53.

[15] 何朝兵.关于Polya罐子模型的几个结论[J].海南大学学报(自然科学版)，2009，27(4)：332-335.

[16] 杜培军.遥感原理与应用[M].北京：中国矿业大学出版社，2006：171-172.

[17] 周辉仁，郑丕谔，牛犇.基于递阶遗传算法和BP网络的模式分类方法[J].系统仿真学报，2009，21(8)：2243-2247.

[18] GEMAN S，GEMAN D.Stochastic Relaxation，Gibbs Distribution，and Bayesian Restoration of Images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1984，6(6)：721-741.

[19] CONGALTONR G，GREEN K.Assessing the Accuracy of Remotely Sensed Data：Principles and Practices[M].Boca Raton，State of Florida：CRC Press，2008：105-119.