ARIMA模型在江苏省社会固定资产投资中的应用
马媛婵
[提要] 投资是拉动经济增长的三驾马车之一,因此研究我国全社会固定资产投资对研究我国经济增长有着重要的现实意义。本文采用江苏省1991~2015年数据,从时间序列定义出发,运用Eviews软件建立ARIMA模型,对历年江苏省社会固定资产进行分析,最后对该模型进行评价,提出不足。
关键词:ARIMA模型;时间序列;固定资产投资
中图分类号:F83 文献标识码:A
收录日期:2018年2月6日
一、引言
1978年的改革开放政策,给我国带来新的发展动力,让经济迅速发展,并取得不俗的成就,社会固定资产总额也持续增加。就江苏省而言:1991年仅为439.98亿元;1993年首次突破1,000亿元达到1,144.2亿元;而2015年则高达45,905.17亿元。而在中国2001年加入WTO之后,来华投资的外商人数大量增加,这也推动了经济策略的改进与发展,促使经济策略有所改变,为经济增长增添新的动力。而江苏作为改革开放的先行地区,经济发展一直处于领先地位。然而,大量投资的增加导致固定资产增长过快,带来了一些新的问题。又由于全社会固定资产投资受多种因素的影响,而各影响因素之间又有着千丝万缕的内在联系。因此,本文将江苏省社会固定资产投资总额看成是一个时间序列,利用已有的历史数据分析该指标的发展趋势,并预测未来值,从而为经济策略的制定提供可靠的理论基础。
二、ARIMA模型简介
如果通过运用时间序列的过去以及当期值,再加上滞后项的干扰,建立模型以后是可以解释时间序列的规律的,这就是随机时间序列。这种模型的优势就在于,如果序列不受时间的变化而变化,那么,我们就可以用过去的数值来预测未知的变量。
实际生活中,大部分时间都是不平稳的,各类现象的平均数、方差等都会随着时间的不同而改变,但是传统的时间序列模型却只能描述平稳序列的内在规律。因此,就需要一种方法,能够将不平稳的序列转化为平稳的序列。通常所用的方法有差分和取对数。就差分这一方法而言,在差分后序列变得平稳,然后用一个平稳的ARMA(p,q)模型作为其基础,那么原始序列则是一个自回归单整移动平均时间序列,记为ARIMA(p,d,q)。它有三种基本模型组成:AR模型、MA模型以及ARIMA模型。
三、实证分析
影响全社会固定资产投资的因素有很多,如经济基础、人口变化、科技因素等,而各影响因素之间又有着千丝万缕的内在联系。所以,如果想要用传统的因果分析法去研究这个问题,就会比较困难,难以区分究竟是何种因素导致固定资产投资的变化。于是本文将以前的全社会固定资产投资数据作为时间序列,利用这些历史数据分析其内在规律,建立相应时间序列模型,并預测未来值。
本文选用1991~2015年的25个年度指标值,这些数据来源于《中国统计年鉴》和《江苏省统计年鉴》,为了使模型的正确性更高,选用前22年的数据进行处理,得出相应的表达式,并用后3年的数据来对该表达式进行检验,最后对2014年及2015年的投资额进行预测。
(一)数据来源及描述。本文对1991~2015年的25个年度江苏省全社会固定资产投资数据进行分析,所有数据来源于《中国统计年鉴》和《江苏省统计年鉴》。表1为选用数据的基本描述统计,图1为1991~2015年我国全社会固定资产投资总额折线图。(表1、图1)

由表1可知,数据随着时间的变化差距较大,由最大值和最小值之间的巨大差距可知,其有较大的标准差。这也就说明,原序列存在异方差,并且是不平稳的序列。由图1可知,曲线向右上方波动,并且增长趋势明显,并且存在异方差。由图1就能简单判断出该序列不平稳,存在时间趋势项。为了更具有说服力,对原始数据进行单位根检验,由结果可知,未经处理的序列没有通过ADF单位根检验,因此原序列不平稳。这一点也进一步说明了该项指标受到多种因素的影响,不适合固定模式的分析。
(二)平稳化处理。为了使初始数据序列更加平稳,对我国固定资产投资总额序列取对数,记为lnXt;一阶差分后的序列记为△lnXt;二阶差分后的序列记为△2lnXt。按二阶差分后数据做序列图,已没有时间项的干扰,可认为已经变为平稳序列。经处理,发现二阶差分后序列平稳。对已经平稳后的序列做相关图。并根据自相关与偏相关图截尾与否选择适合的时间序列模型。如果自相关是拖尾,偏相关截尾,则用AR算法;相反的话则用MA算法;如果自相关和偏相关都是拖尾,则用ARMA算法。在该例中,PACF图和ACF图均是拖尾的,因此该序列适合ARMA模型。又由于序列是经过二阶差分后才平稳,所以这里选用ARIMA模型。
(三)ARIMA(p,d,q)模型的建立。通过上述分析,本文选择ARIMA(p,d,q)模型,并从上述单位根检验中可知d=2。ARIMA(p,d,q)模型中p、q这两个参数分别通过自相关及偏相关图推出。相关系数AC与偏相关系数PAC在K=2与K=4时都与0有显著差异。因此,设定模型为ARIMA(2,2,4),并先假设存在常数项。
在假设模型为ARIMA(2,2,4)的情况下常数项和部分系数都没有显著性,因此不能通过t检验,因此需要对模型进行修正。修正后的结果如表2所示。(表2)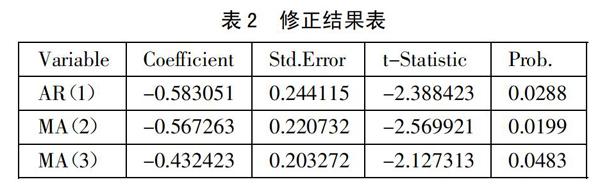
由表2可知,所有系数都是显著的,可以通过检验。于是将模型ARIMA(1,1,4)修正为ARIMA(1,2,3),并得到如下表达式: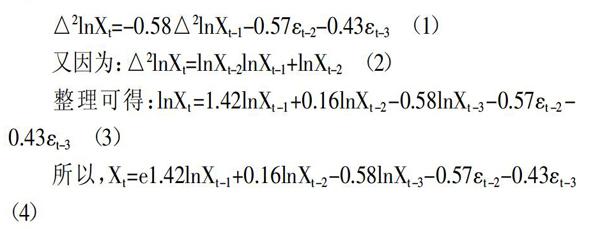
(四)模型的诊断。运用模型(4)对结果进行拟合回归,可以得到相应的拟合值和残差图。实际值与拟合值相比较为接近,且自相关与偏相关值基本都在置信区间内。
由于估计模型时使用的是1991~2013年的数据,所以可以使用2014年、2015年这两年的数据对模型进行估计。具体预测结果如表3所示。(表3)
四、模型评价
建立ARIMA模型时,本文选择1991~2015年江苏省固定资产投资额作为研究对象,通过平稳性检验、自相关与偏自相关等检验确定模型相关参数,得到ARIMA(1,2,3)模型。用模型对2014年、2015年的江苏省固定资产投资做预测,得到的预测值与实际值拟合效果较好,误差分别为4.1%和19.8%。由此可见,随着ARIMA模型预测期间增大,预测误差会逐渐增大。在短期预测方面,与其他的预测方法相比,该种预测的准确度还是比较高的。因此,建立ARIMA模型对预测短期除此之外,此处的样本量较少,仅有25个,要想有更好的拟合和预测效果,样本量应该越多越好。
主要参考文献:
[1]倪宁宁.基于拓展ARIMA模型的全社会固定资产投资拟合及预测[J].统计与决策,2016.13.
[2]潘静,张颖,刘璐.基于ARIMA模型与GM(1,1)模型的居民消费价格指数预测对比分析[J].统计与决策,2017.20.
[3]师思.ARIMA模型在固定资产投资变化率预测中的运用[J].统计与决策,2009.10.
[4]李惠.ARIMA模型在我国全社会固定资产投资预测中的应用[J].对外经贸,2010.7.
[5]尹炜锋.河北省固定资产投资需求分析预测[D].天津大学,2013.

