基于PSO优化LSSVM在基坑开挖过程中周围建筑物沉降预测研究

李海鹏 胡锦伟 王加志 黄志艳

摘要：本文提出一种用粒子群优化算法来确定LSSVM参数的方法。该方法是在对LSSVM进行分析的基础上，融合PSO的群搜索特征来提高LSSVM预测精度。文章最后采用昆明市某基坑周围建筑物沉降数据对此模型进行了验证，并与其他算法进行了对比分析，计算结果表明用该模型进行沉降预测相比其他算法具有较快的收敛速度和更高的预测精度。

Abstract： This paper presents a method of determining the parameters of LSSVM using particle swarm optimization algorithm. The method is based on the analysis of LSSVM， and combines PSO's group search features to improve LSSVM prediction accuracy. At last， the model is verified by the settlement data of buildings around a foundation pit in Kunming and compared with other algorithms. The calculation results show that the settlement prediction using this model has faster convergence speed and more High prediction accuracy.

关键词：基坑开挖；沉降预测；PSO算法；LSSVM模型；参数优化；预测精度

Key words： foundation pit excavation；settlement prediction；PSO algorithm；LSSVM model；parameter optimization；prediction accuracy

中图分类号：TV551.4+2 文献标识码：A 文章编号：1006-4311（2018）14-0125-03

0 引言

由于基坑工程的特殊性导致了在基坑开挖引发周围建筑物沉降的观测时间短，因此基坑开挖引发周围建筑物的沉降数据就是小样本数据。本文利用一种基于粒子群优化算法（PSO），对最小二乘支持向量机（LSSVM）供水量预测模型参数进行优化。为了验证模型的可靠性，本文采用某市实测基坑周围建筑物沉降数据对比分析了PSO算法，遗传算法，并对上述两种模型和BPNN的预测精度进行定量分析。

3 实例分析

基于上述方法对昆明某基坑周围建筑物竖向位移进行预测。该基坑最大开挖深度16m，支护形式为桩锚支护，场地形式较为复杂需对周围环境建筑物进行竖向位移监测。图1为基坑及基坑周边环境及测点布置平面图。

本文以测点jk5、jk6的作为本文模型的研究数据，以前56個数据作为训练样本，以后7个数据作为测试样本。笔者先将沉降数据进行相空间重构，在进行相空间重构时，采用了互信息法[14]和G-P法[15]求得测点jk5的τ=3，m=4测点jk6的τ=6，m=5其中τ为延迟时间，m嵌入维数。再依据BIC信息准则选取邻近相点K=7。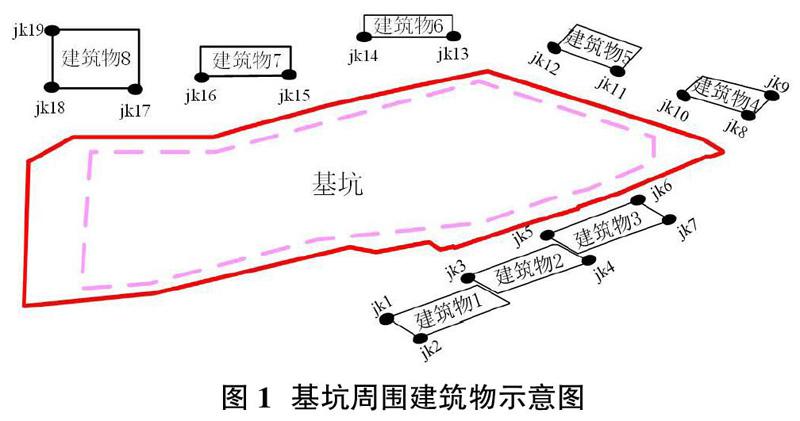

本文应用了使用最广泛的BP神经网络对基坑周围建筑物沉降量进行预测。三种模型的预测效果如图2，图3所示。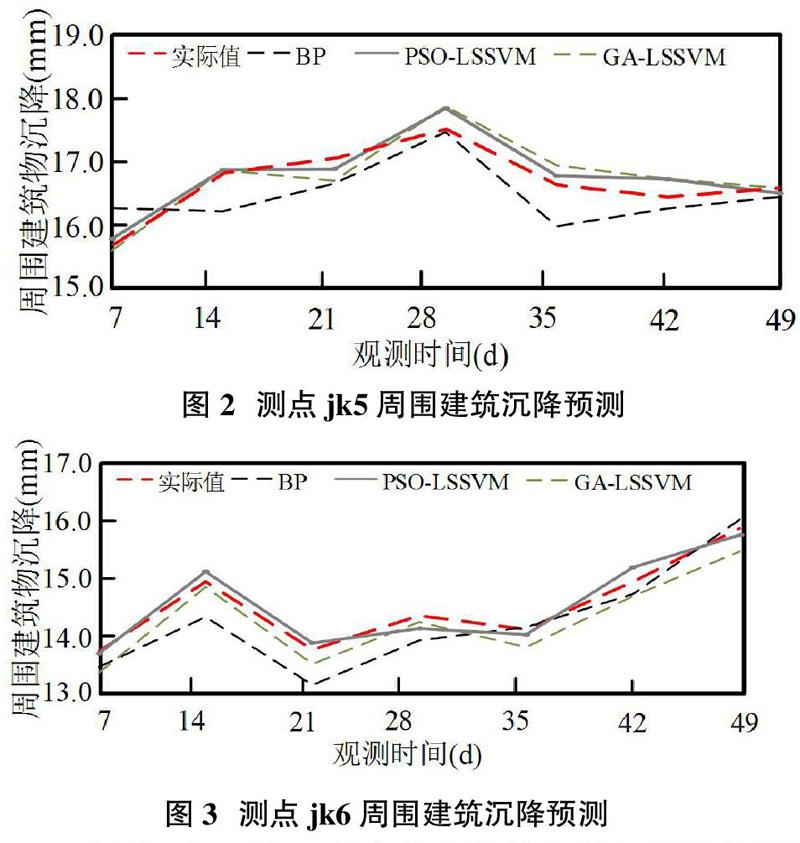

由图可知，这四种方法都能较好的把握基坑周围建筑物沉降的总体趋势，但对局部细节预测存在一定的差异。本文采用平均绝对误差（MAPE）对预测结果进行分析，如表1、表2所示。PSO与LSSVM模型的预测精度最高，而单纯的BP神经网络预测精度最低。本文提出的PSO算法寻优速度最快，收敛所用的迭代次数最少，平均绝对误差最小，充分显示了该算法在沉降量预测方面上具有良好的信息收集能力和对全局最优解的掌控能力。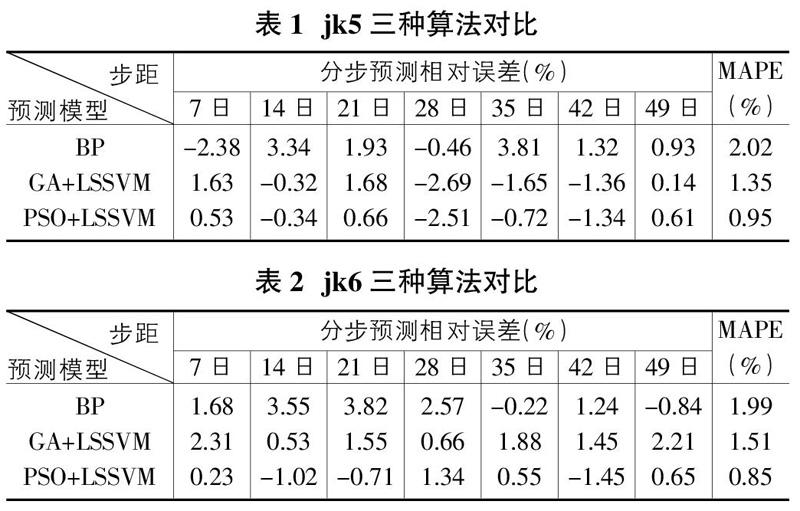

4 结论

本文采用昆明市某基坑周围建筑物沉降的实测数据对多种模型预测结果进行对比分析，得出以下结论：

①采用PSO算法对LSSVM设计参数进行优化，在LSSVM的参数寻优上展现了其收敛速度快、结果准确等优点，有效地解决了在非线性沉降量上难以建模的问题。

②利用本文方法对基坑开挖过程中对周围建筑物的沉降进行预测，平均绝对值误差为0.90%，与GA-LSSVM， BP算法相比，具有更高的预测精度。

③本文所使用的模型易于通过软件实现，为其它相关研究的开展提供了崭新的思路。

参考文献：

[1]杨涛，李国维，樊琨.基于人工神经网络的公路软基沉降预测模型[J].上海理工大学学报，2003（02）：117-120.

[2]刘思峰.灰色系统理论的产生与发展[J].南京航空航天大学学报，2004（02）：267-272.

[3]刘晓，曾祥虎，刘春宇.边坡非线性位移的神经网络–时间序列分析[J].岩石力学与工程学报，2005（19）：101-106.

[4]李德江，花向红，李涛等.基于支持向量机的建筑物沉降预测模型研究[J].测绘工程，2009（03）：29-31.

[5]吴清海，李惠芳.变权组合模型在沉降预测中的应用[J].测绘科学技术学报，2009（02）：118-120，124.

[6]曹净，丁文云，赵党书，等.基于LSSVM-ARMA模型的基坑变形时间序列预测[J].岩土力学，2014（S2）：579-586.

[7]郭树荣，丛旭辉.基于灰色组合模型的基坑周边建筑物沉降预测[J].建筑科学，2016（03）：89-93，99.

[8]VAPNIK V N. The nature of statistical learning theory[M]. New York： Springer， 1995.

[9]SUYKENS J AK， Van GESTEL T， BRABANTER D E. Least squares support vector machines[M]. Singapore：World Scientific， 2002.

[10]崔建明，刘建明，廖周宇.基于SVM算法的文本分类技术研究[J].计算机仿真，2013（02）：299-302，368.

[11]赵波，曹一家.电力系统无功优化的多智能体粒子群优化算法[J].中国电机工程学报，2005，25（5）：1-7.DOI：10，3321/j.issn：0258-8013.2005.05.001.

[12]唐雪琴，王侃，徐宗昌，等.基于MAPSO算法的小波神经网络训练方法研究[J].系统仿真学报，2012，24（3）：104-108.

[13]何井運，郑亮.基于混沌相空间重构公路路堤沉降预测模型[J].交通标准化，2009（17）：18-22.

[14]李峰，宋建军，董来启，等.基于混沌神经网络理论的城市地面沉降量预测模型[J].工程地质学报，2008（05）：715-720.

[15]吕小青，曹彪，曾敏，等.确定延迟时间互信息法的一种算法[J].计算物理，2006（02）：184-188.

[16]陈丽琳.基于多嵌入维数的时用水量LSSVM组合预测[J]. 机电工程，2012（07）：869-872.

[17]付强，李晨溪，张朝曦，等.关于G-P算法计算混沌关联维的讨论[J].解放军理工大学学报（自然科学版），2014（3）：275-283.DOI：10.7666/j.issn.1009-3443.20130110001.

[18]GOKULAN B. P，SRINIVASAN D，Distributed geometric fuzzy multiagent urban traffic signal control[J]. IEEE Transactions on Intelligent Transportation Systems，2010，11 （3）： 714 -727.