异步轧制等效应变速率的计算模型

李立新 郑良玉 肖 麟 童泽琼

(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北武汉 430081)

异步轧制与同步轧制相比，具有板形好、尺寸精度高、轧制压力低、板带加工效率高、道次变形大等特点，在硅钢、铝板材等金属轧制中取得了良好的效果[1- 4]。异步轧制根据单一应变路径分类有：(1)上下轧辊半径相同，轧辊转速不同；(2)上下轧辊转速相同，轧辊半径不同；(3)上下轧辊转速、半径都相同，但上下轧辊与轧件接触的摩擦条件不同。这三种异步轧制过程，前两种是上下轧辊的线速度不同，第三种则是轧辊与轧件的摩擦条件不同，最终都导致轧件与轧辊接触面上的摩擦力中性面发生移动，所以上下接触面的摩擦力会形成一个额外的搓轧区。由于额外搓轧区的存在，会对轧制板材的织构及晶粒大小造成影响[5- 8]，同时使得接触区应力、应变、应变速率更为复杂。

Saito Y等[9]在2 mm×20 mm×430 mm的轧制试样中部插入同种材料的长2 mm、直径3 mm的圆柱棒，通过改变轧辊的摩擦条件，试样高速轧制后，观察圆柱棒的变形情况，并在平面变形占主导的条件下，提出了异步轧制试验压缩应变和剪切应变与剪切角的关系式，以及等效应变的计算方法。Ko Y G等[10]、Ding Y等[11]、Lee K M等[12]则利用Satio Y提出的公式，同样采取插片法得到剪切应变，间接验证了该计算公式的准确性。Ma C Q[13]等认为,异步轧制是沿轧件法向的压缩应变和沿轧制方向的剪切应变的平面应变状态，在几何学基础上，对异径轧制剪切应变计算公式作了相应修正，提出了同径异速轧制剪切应变公式，并在有限元模拟基础上作了相关计算。两种剪切应变公式同时建立在实际验证的基础上，可以认为是等效的，联立两式可以得到剪切角的计算方法。Beausir B等[14]认为,在异步轧制过程中，剪切应变速率和压缩应变速率存在一个比例系数p，并推导出p与剪切角和压下率的计算公式，但关于压缩应变速率未给出相关计算方法。

本文结合轧制变形相关理论，推导了压缩应变速率计算公式，在上述理论基础上，计算了等效应变速率。为验证推导的等效应变速率公式的合理性，由于直接验证较为困难，故采用JMAK方程和轧制退火试验来间接验证。具体是利用推导公式计算得到的等效应变速率代入JMAK方程，拟合异步轧制理论再结晶软化率计算公式，再利用该拟合公式计算同步轧制理论再结晶软化率，与实际测量的再结晶软化率进行对比验证。本文试验采用同径异速异步轧制，试样再结晶软化率通过测量退火前后试样硬度的变化来计算。

1 理论推导

1.1 剪切角的确定

宽厚比较大的板材轧制时可以忽略宽展，近似处理为平面应变,即沿轧件法向的压缩应变以及沿轧制方向的剪切应变和拉伸应变。在异步轧制中，剪切应变γ存在Satio Y提出的关系：

(1)

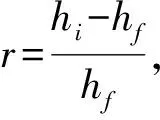
(2)

式中：θ为剪切角。

异步轧制时的剪切应变与上下轧辊速度之间的关系，还可用Ma C Q等提出的公式计算：

(3)

式中：hi和hf表示试样的初始厚度及轧后厚度(m)，R表示轧辊半径(m)，v1和v2分别表示上下轧辊的线速度(m/s)。

联立两种剪切应变公式，可确定tanθ=f(hi,hf,R,v1,v2)。

1.2 异步轧制压缩应变速率和等效应变速率的确定

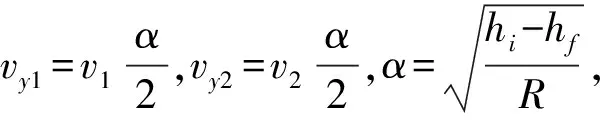
(4)

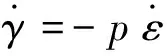
(5)

其中，系数p>0，并且p与剪切角θ存在以下关系：

(6)

由式(6)与剪切角的计算公式确定p=g(hi,hf,R,v1,v2)。

=f2(hi,hf,R,v1,v2)

(7)

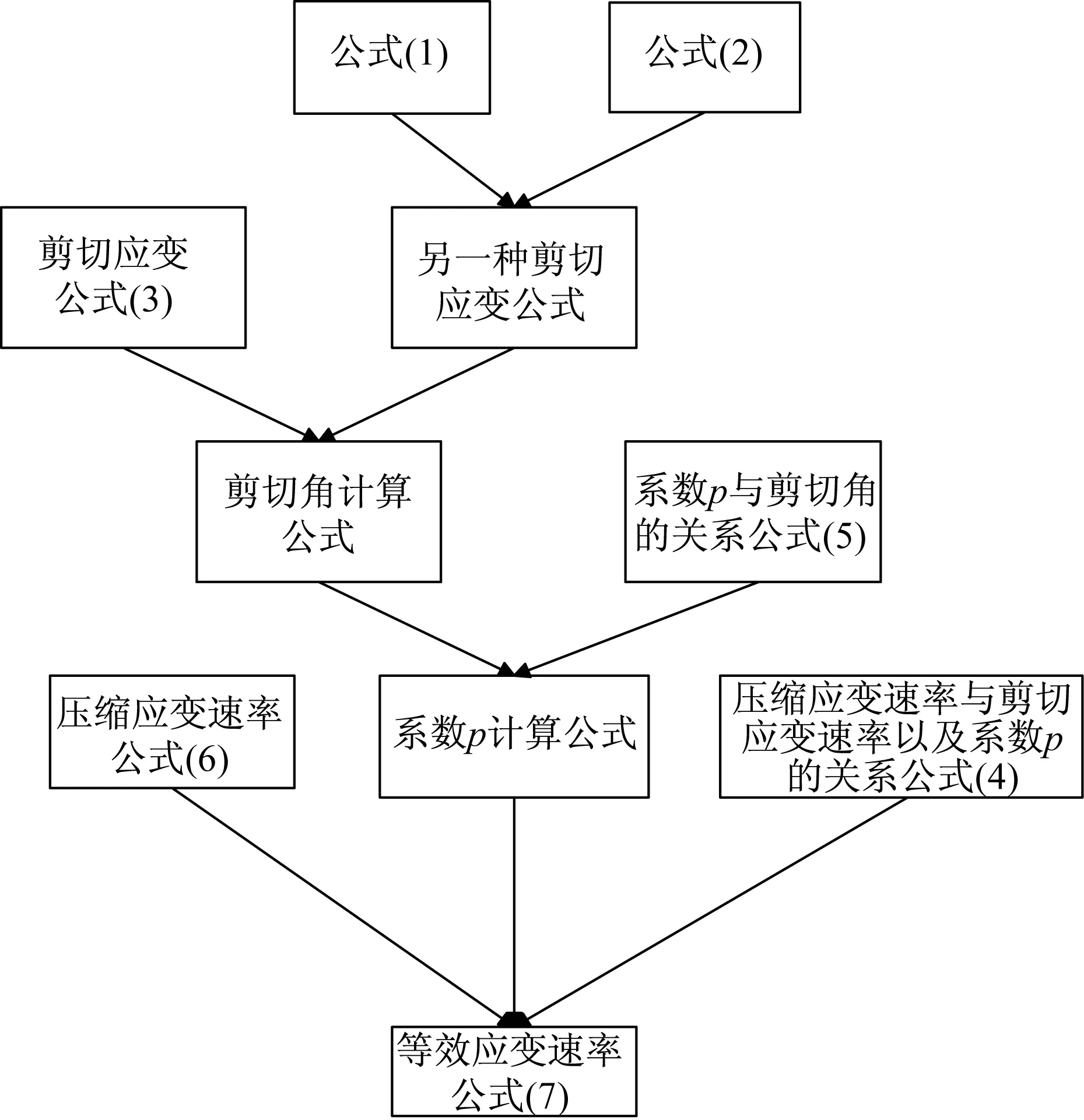
图1 公式推导流程图Fig.1 Flow chart of equation derivation

2 试验验证

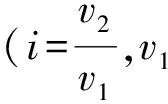
表1 试样的化学成分(质量分数)Table 1 Composition of the samples (mass fraction) %

2.1 试验结果

再结晶软化率计算公式为：

(8)

式中：H1表示加工硬化后试样的硬度，H2表示退火相应时间试样的硬度，H3表示完全退火后试样的硬度。

再结晶软化率可以根据Avrami方程[15- 16]描述如下：

(9)

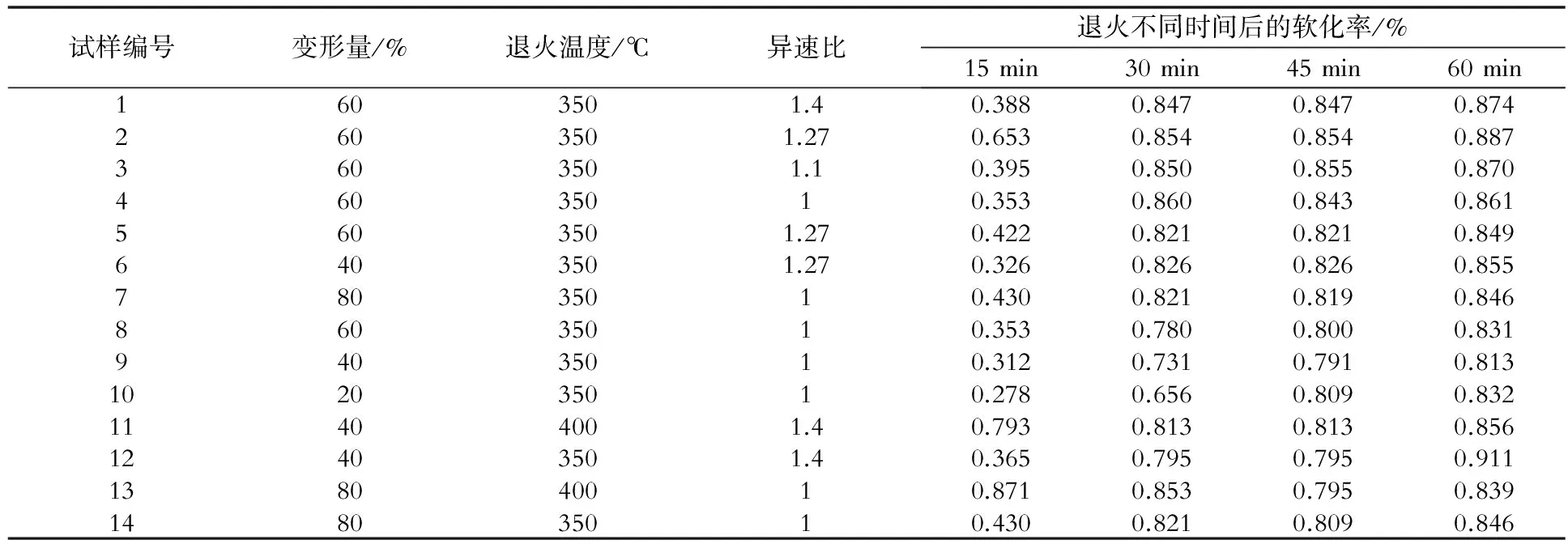
表2 试验参数和结果Table 2 Experimental parameters and results

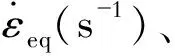
(10)

式中：A、p、q、s都为材料常数，Q为激活能(J/mol)，R为气体常数(J/(mol·K))。

将式(9)变换一下，对变换后方程和式(10)取自然对数，联立两等式可获得方程：

(11)

式中：α0、α1、α2、α3、α4均为常数。

根据表2试验数据(其中5、8、15号铝样作为对比试验)进行多元线性回归，得到异步轧制回归方程：

(12)

在显著性水平0.001下，通过F分布表查得临界值Fα(4,16)=7.94，观测值F0=13.739 5，F0>Fα，故回归方程是显著的。将此方程推广到同步轧制试验结果中，计算得到同步轧制的理论再结晶软化率，并与试验结果进行比较。退火30 min再结晶软化率的理论值与试验值对比如图2所示。

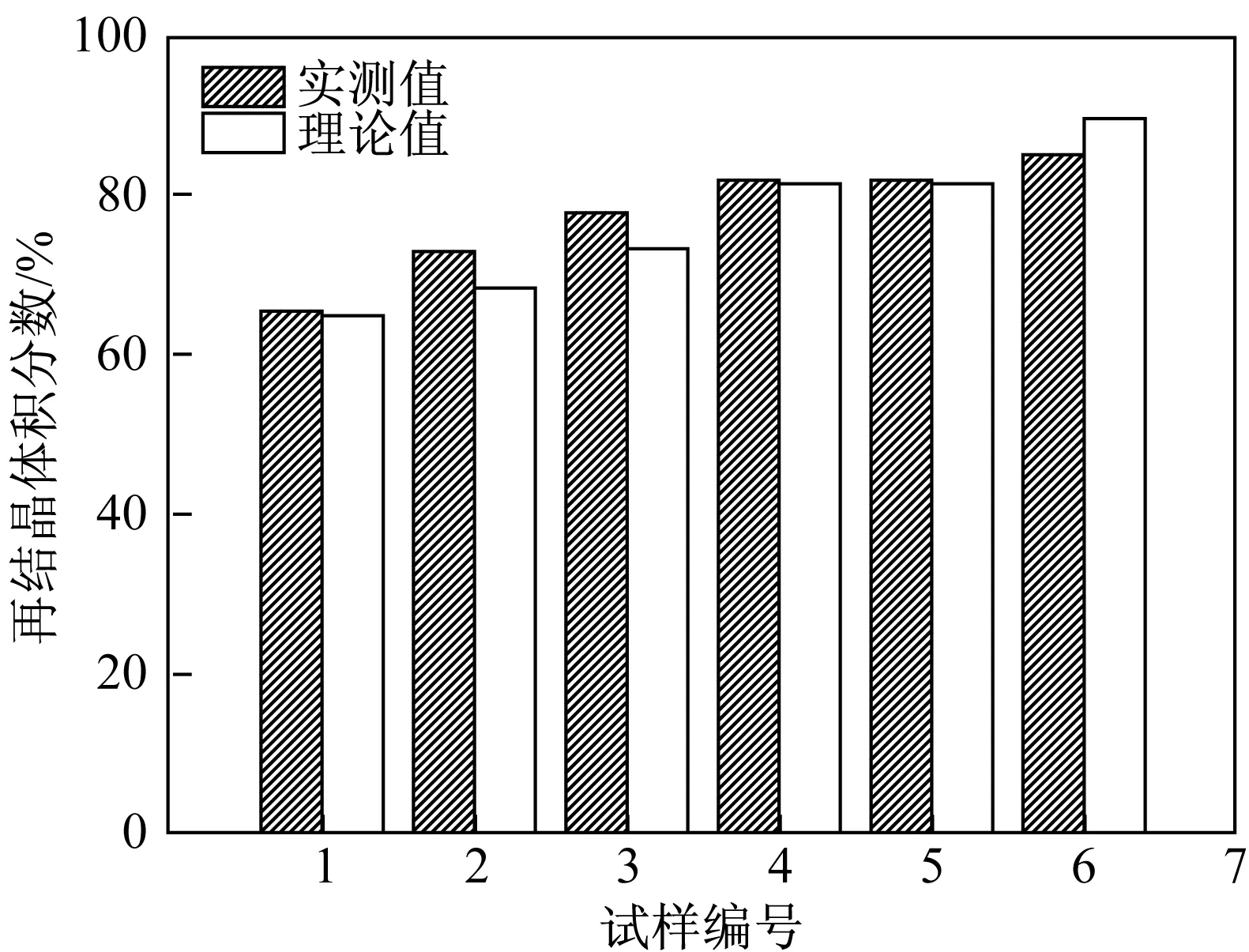
图2 退火30 min再结晶软化率理论值与试验值对比Fig.2 Comparison of theoretical and experimental values of the recrystallization softening rate after annealing for 30 min

从图2可以看出，再结晶软化率的试验值和理论值最大误差为5.42%左右，最小为0.392%，考虑到实际测量等因素的影响，该误差是可以接受的。可以判定该回归再结晶软化率计算公式对同步再结晶软化率计算是准确的，间接证明了异步轧制等效应变速率计算公式在异速比i=1的情况下，计算同步轧制等效应变速率也同样适用。

2.2 讨论

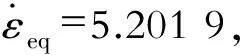
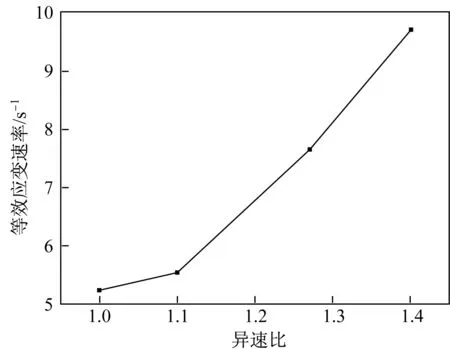
图3 异速比对等效应变速率的影响(压下率为60%)Fig.3 Effect of rolling speed on equivalent strain (reduction rate of 60%)

压下率对等效应变速率的影响如图4所示。可以看出，相同异速比，压下率越大，等效应变速率越大。主要原因在于相同异速比条件下，压下量增加，压缩应变速率增大，并且压缩应变速率影响较大，剪切应变速率增加，最终等效应变速率增大。同时可以看出，相同压下率，较小异速比下，等效应变速率变化较小，这一点与异速比对等效应变和等效应变速率的影响相对应。

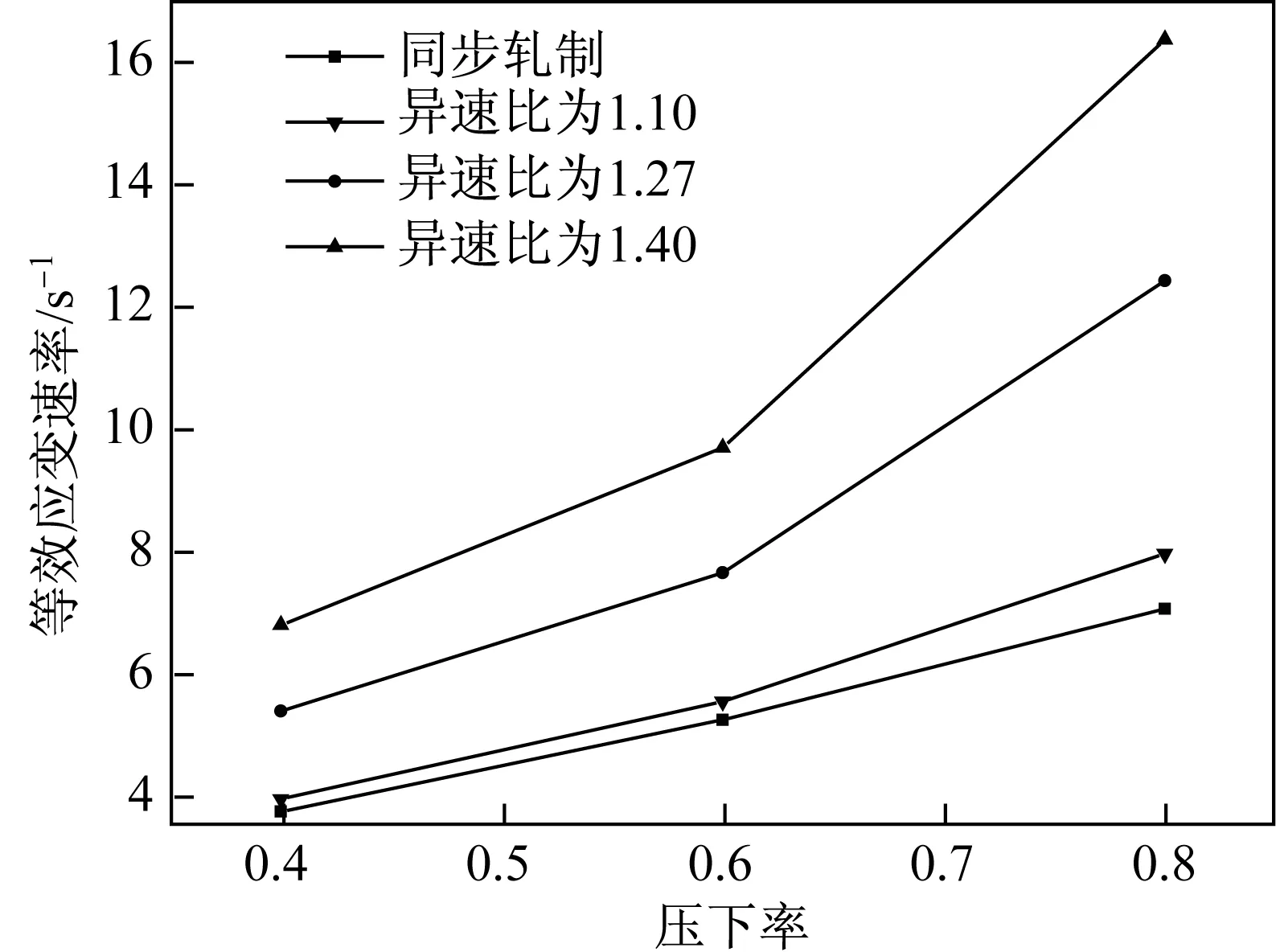
图4 压下率对等效应变速率的影响Fig.4 Effect of rolling reduction rate on equivalent strain rate

3 结论

(1)本文推导的计算模型基于轧制基本参数—轧辊转速、轧辊半径、异速比、压下量，尽管形式相对复杂，但能有效简便计算轧制等效应变速率。

(2)影响轧制过程中等效应变速率的因素：相同压下率等效应变速率在异速比i=1.030 1取得最小值；相同异速比下：较小异速比时，压下率越大，等效应变速率变化不明显；较大异速比时，压下率越大，等效应变速率变化较大。

[1] 王忠堂,宋广胜,张士宏.异步轧制AZ31镁合金板材的孪晶组织及织构[J].材料热处理学报, 2013, 34(10):62- 66.

[2] 江海涛,段晓鸽,蔡正旭,等.异步轧制AZ31镁合金板材的超塑性工艺及变形机制[J].材料工程, 2015, 43(8):7- 12.

[3] 李冰峰.异步轧制技术及其在铝合金中的应用[J].有色金属加工,2013,42(5):5- 7.

[4] 刘刚,莫成刚,李超.异步轧制硅钢薄带的固体渗硅[J].钢铁,2016,51(3):68- 72.

[5] 左玉波,付兴,崔建忠.异步热轧铝合金厚板的剪切变形和板形控制[J].中国有色金属学报(英文版), 2014, 24(7):2220- 2225.

[6] WRONSKI S, GHILIANU B, CHAUVEAU T, et al. Analysis of textures heterogeneity in cold and warm asymmetrically rolled aluminium[J]. Materials Characterization, 2011, 62(1):22- 34.

[7] MA C Q, HOU L G, ZHANG J S, et al. Microstructures and properties of asymmetrical rolled 7050 Al alloy plate with bending behavior optimization[J]. Materials Science & Engineering A, 2016, 657(1):322- 330.

[8] MA R, WANG L, WANG Y N, et al. Microstructure and mechanical properties of the AZ31 magnesium alloy sheets processed by asymmetric reduction rolling[J]. Materials Science & Engineering A, 2015, 638(2):159- 164.

[9] SAITO Y, SAKAI T, MAEDA F, et al. Deformation and recrystallization behavior of ferritic stainless steel in high speed hot rolling[J]. Tetsu- to- Hagane, 1986, 72:799- 806.

[10] KO Y G, SUHARTO J, LEE J S, et al. Effect of roll speed ratio on deformation characteristics of IF steel subjected to differential speed rolling[J]. Metals & Materials International,2013,19(3):603- 609.

[11] DING Y, JIANG J H, SHAN A D. Microstructures and mechanical properties of commercial purity iron processed by asymmetric rolling[J]. Materials Science & Engineering A, 2009, 509(1/2):76- 80.

[12] LEE K M, LEE H C. Grain refinement and mechanical properties of asymmetrically rolled low carbon steel[J]. Journal of Materials Processing Technology, 2010, 210(12):1574- 1579.

[13] MA C Q, HOU L G, ZHANG J S, et al. Influence of thickness reduction per pass on strain, microstructures and mechanical properties of 7050 Al alloy sheet processed by asymmetric rolling[J]. Materials Science & Engineering A, 2016, 650(4):454- 468.

[14] BEAUSIR B, BISWAS S, DONG I K, et al. Analysis of microstructure and texture evolution in pure magnesium during symmetric and asymmetric rolling[J]. Acta Materialia, 2009, 57(17):5061- 5077.

[14] 蒋莉萍,王军,肖振宇,等.室温多向锻压AZ31镁合金的静态再结晶行为[J].中国有色金属学报,2015, 25(11):3051- 3059.

[16] 彭聪辉,常辉,胡锐,等.Haynes230高温合金的静态再结晶动力学[J].航空材料报,2011, 31(2):8- 12.

[17] PARK J J. Finite- element analysis of severe plastic deformation in differential- speed rolling[J]. Computational Materials Science, 2014, 100(121):61- 66.

收修改稿日期：2017- 06- 05