一种采用改进融合观测器的同步磁阻电机位置估算算法

杜逸康，廖勇，林豪，李福

（重庆大学电气工程学院，重庆 400044）

0 引言

同步磁阻电机是一种转子无需永磁体和励磁绕组的无刷电机，转子结构如图1示，依靠转子的凸极性产生磁阻转矩，结构简单，成本较低，调速性能好[1]。若能实现同步磁阻电机的无位置传感器控制，可将同步磁阻电机推广到各类对成本控制要求高，对机械结构空间限制多的场合加以利用，并推动同步磁阻电机向高速化发展。针对同步磁阻电机的角度估算问题，有诸多学者进行了研究与讨论。

图1 同步磁阻电机转子结构示意图Fig.1 The rotor structure of Synchronous Reluctance Motors

利用电机数学模型及可获取的电压电流信号，直接解算电机转子位置角，是常用的一类无位置传感器控制方法，如通过计算电机转子磁链获得转子位置角[2-4]，或跟踪电机的扩展反电势，解算转子位置角信息[5]。通过采用各类全维或者降维观测器，对同步磁阻电机系统进行在线观测，并估算转子位置，也是常用的实现手段[6-9]。这类方法运算简单，但在低速段，由于漏抗压降和电阻压降占比较大，反电势较小，在零速时，反电势为零，因此这类方法只能用于中高速，同时，电机参数的准确性对这类方法的影响极大，电机参数的不准确会导致该类方法得到的转子位置产生较大误差[7,10,11]。而在低速段采用其他方法，会产生两种方法有效速度区间交叉时，角度如何切换的问题[12]。

为弥补上述利用电机模型的方法在低速段及零速点的问题，高频信号注入法通过在机端注入高频信号，人为使得转子的凸极性在高频反馈信号中易于检测，从而实现跟踪转子位置角[13-16]。高频注入法分为旋转信号注入法和脉振信号注入法两种。旋转信号注入法通过在机端注入一个高频旋转的电压矢量，跟踪反馈电流信号中高频信号的相位，并直接计算注入信号与反馈信号的相位差得到转子位置信息。脉振信号注入法在同步旋转轴系d轴方向上注入脉振电压小信号，利用定子电流中高频信号分量作为参考坐标轴系与实际坐标轴系间的角差信息，调整参考坐标轴系的角度从而实现跟踪[15]。相比旋转信号注入法，脉振信号注入法在同样的注入频率和功率下可以产生更大的参考轴系误差角以便于追踪[17]。高频信号注入法类方法具有共同的问题，即在经过采样和信号解析电路及控制系统的动作滞后，反馈信号的相位产生了一定的滞后偏差，这会导致在未进行相位补偿而直接滤波和解算坐标系角度误差信息时，有效信号信噪比降低的问题，严重情况下会导致锁相环无法正确跟踪。

基于上述现有的理论研究，本文提出一种低速段采用改进脉振高频电压信号注入法，高速段采用有效磁链观测器，两者共用同一个角度锁相环的同步磁阻电机角度估算方法。低速段仅用低通滤波器，并利用原方法未利用的d轴的电流信号，从dq轴电流信号的乘积中获得位置误差信号，从而避免原方法解算过程中可能导致有效信号信噪比较小的问题。同时，高速段的磁链观测器与低速段的信号注入法共用同一个角度锁相环，利用权重函数表进行角度切换，提供更平滑的角度观测效果。

1 同步磁阻电机的数学模型

将同步磁阻电机简化为同步旋转坐标轴系下的理想电机模型，忽略磁滞损耗、杂散损耗、饱和效应，在dq轴系中电压方程如下[18]：

式中ud，uq为dq轴下的定子电压；id，iq为定子dq轴电流；rs为定子电阻；Ld，Lq为dq轴电感；ωe为转子电角速度。同步磁阻电机的转矩表达式为：

其中，P为电机转子极对数。

图2 有效磁链矢量关系示意图Fig.2 Active flux vector diagram in dq synchronous reference frame

2 有效磁链观测器

有效磁链观测器（Active Flux Observer）的思想为将任意交流电机的转矩公式中，与iq电流相乘的磁链量定义为有效磁链量，从而将电机模型转化为一个理想的隐极同步电机[19]。在此定义下，有效磁链始终与d轴方向平行，代表产生转矩的励磁磁链量，跟踪有效磁链即可得到d轴位置。

同步磁阻电机的有效磁链量定义为：

此时，式（3）可表示为如下形式：

而定子磁链量在dq轴系下可表示为：

对同步磁阻电机而言，由于转子上无任何励磁结构，励磁完全是由定子提供的，因此定子磁链量即为转子磁链量。将上述矢量表示在dq轴系中，可知不管电压电流矢量如何变化，有效磁链量方向始终与d轴一致。因此得到了磁链矢量，即可求出转子角度。

在磁链计算中，逆变器的非线性效应，积分器的零漂效应，均会造成直接积分得到的有效磁链产生偏移[20]，因此在应用中，有效磁链计算式（7）中具有一项积分误差补偿量ucomp，该量由角度估算后，利用电流模型计算的磁链与电压模型得到的磁链对比求差得出。

有效磁链观测器完整结构如下X示，而转子位置角可采用上式（8）直接计算得到。其中，fs为采样时间，k和k-1分别代表现在的采样点和前一个采样点。

图3 有效磁链观测器结构图Fig.3 Active flux observer structure diagram

3 改进信号注入法

本文采用高频脉振电压信号注入法。电机运行时，在参考d轴上注入一个脉振高频小电压信号，当参考旋转坐标轴系与真实同步旋转坐标轴系有偏移角时，在参考dq轴方向上均有感应的反馈高频电流信号，推导如下：

在参考轴系的d轴上注入高频脉振电压信号：

图4 参考坐标系与真实坐标系对应关系Fig.4 The relationship between real dq frame and refrence dq frame

由于参考轴系与真实轴系中间存在的偏角，可得到真实坐标轴下的注入信号为：

在式（10）的高频激励信号下，由于反馈高频电流较小，可忽略式（1）、式（2）中的电阻压降项，运动电势项由于转速较低也可忽略。将基波下的同步磁阻电机数学模型简化为高频下频域表达式后，将复频域算子s用jω替换，得到方程（11）：

其中ld，lq为高频dq轴电感。将式（10）代入式（11），可得高频电流激励为：

其中：

在原文献中，由于式（12）中q轴上的高频电流反馈在Δθ为零时也为零，因此通过将该高频电流转为直流量，即可作为PI锁相环的角差信号输入，从而实现高频信号注入法跟踪角度[14]。而转为直流量的这一过程是将该信号与系统产生的高频同相信号相乘实现的，当两者由于A/D转换过程及采样过程产生相差时，会造成有效信号幅值的减弱。

对这一问题，本文采用如下的改进方法，将dq轴反馈电流信号相乘：

将dq轴反馈信号视作高频反馈信号和基频直流反馈信号的组合，因此式（14）相乘的结果中，可找到dq轴电流高频反馈信号相乘的结果，而由于dq轴电流经过的是相同的采样和处理环节，相位滞后应是相同的，因此上述操作的效果与原方法中令q轴电流与系统产生的高频信号相乘的结果是一致的，但由于无相位滞后，因此有效信号的幅值未衰减。因此采用下图5中的滤波器组合结构，就可以得到与原方法类似的偏角信号，如式（15）所示。

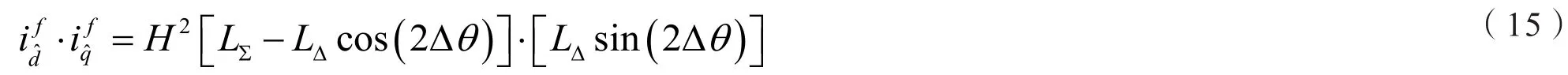
其中：

显然式（15）中的信号具有和式（12）中相似的效果，均可以作为PI环节跟踪的对象。

4 改进融合角度观测器

采用本文提出的改进高频信号注入法和有效磁链观测器法，可分别得到中高速域下与低速域下的转子位置角观测值与电机速度观测值。在升速或降速过程中，一般采用加权平均的方法处理两种方法速度交叉段的角度与速度估算值。这会带来如下问题：当高频注入法仍处于工作状态时，高频信号注入不能切断，这会导致同一时刻运行的磁链观测器中得到的结果包含高频谐波，如利用式（8）的方法直接解算，会导致磁链观测器得到的角度有抖动，速度则可能产生极大的震荡，这一结果会通过加权算法引入最后的综合结果，使得电机失稳[3]。而采取对磁链信号进行滤波等方式又会人为增加磁链信号的相差及算法的运算量，这两者都会使得角度信号的处理变得更加复杂。

为应对上述问题，本文提出一种改进的融合角度观测器，采用下图6所示的结构，高速段仅采用磁链观测器得到的角度信号，抛弃直接计算的速度信号，将两种方法得到的参考轴系角差信息按照以速度为参量的比例输入锁相环，在300 rpm以上仅采用磁链信号，在100 rpm下仅采用高频注入法信号，在100～300 rpm之间则根据速度得出不同的比例值，确保两种方法的投入和切出都是平滑的。由于角度的综合是通过锁相环的方式进行的，在低速和中速时，磁链观测器由于角差信号输出占比，因此可以去除信号注入带来的抖动对最终结果的影响，而速度锁相环对角度的波动具有一定的滤波能力，也保证了最终输出结果的平滑程度。

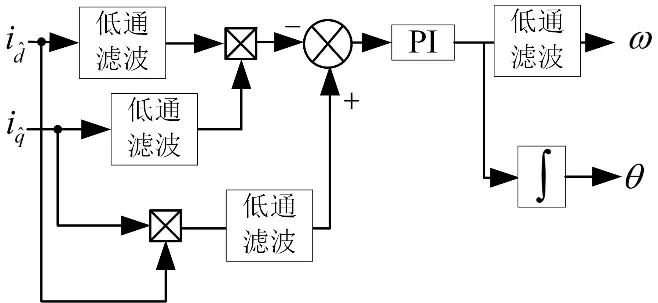
图5 改进的反馈高频信号处理方式Fig.5 Improved HFSI signal resolving method

图6 融合观测器基本结构图Fig.6 The structure of fusion observer

5 实验验证

本文前述的角度估算方法在一台10 kW同步磁阻电机上进行了实验验证，电机参数见下表1。实验平台为快速原型控制平台dSPACE ds1103系统，可直接利用MATLAB/Simulink模型进行算法开发和实验，试验平台及设备照片见图7、图8。

表1 同步磁阻电机参数表Table1 Parameters of Synchronous Reluctance Motor

图7 试验平台照片Fig.7 Experiment platform photo

图8 同步磁阻电机及其他实验设备Fig.8 Synchronous reluctance motor and other equipment

图9至图11为低速段电机在空载状态由30 rpm升速至40 rpm后的信号注入法工作波形。由图9的速度观测波形可知，本文改进信号注入法相较原方法，观测得到的速度误差更小，在升速的过程中动态跟踪性更好，无明显振荡，而原方法在申诉过程中产生了明显的振荡。且相较本文改进接近零的角度观测误差，原方法在跟踪角度上存在一个较大的观测误差，由图11可知。

图12至14为融合观测器在速度切换域前后一段升速过程的波形。电机在空载状态由100 rpm 至300 rpm稳定。由图12及13可见，融合观测器从信号注入法切换至磁链观测器的过程中，无明显震荡或抖动，速度与角度跟踪都保持了很高的精度，由图14也可知全过程中融合观测器角差略有波动，但基本保持在零附近。体现了本文所述融合观测器的优越性和可靠性。

图9 原高频注入法与本文改进方法速度观测对比图Fig.9 Improved HFSI method and original method speed comparation

图10 原高频注入法与本文改进方法角度观测对比图Fig.10 Improved HFSI method and original method position comparation

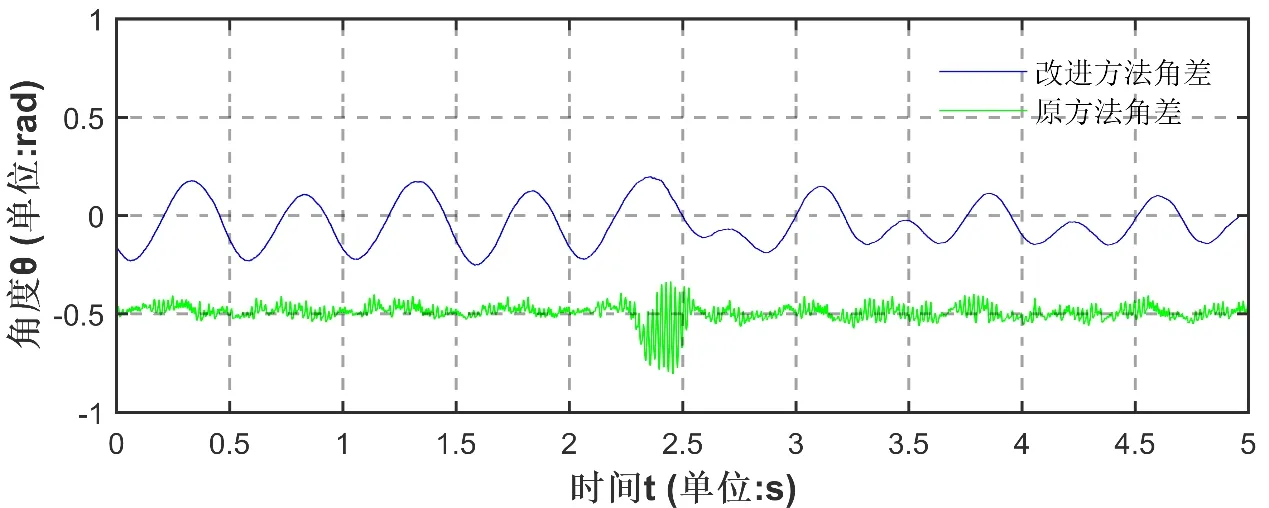
图11 原高频注入法与本文改进方法角差对比图Fig.11 Improved HFSI method and original method position error comparation

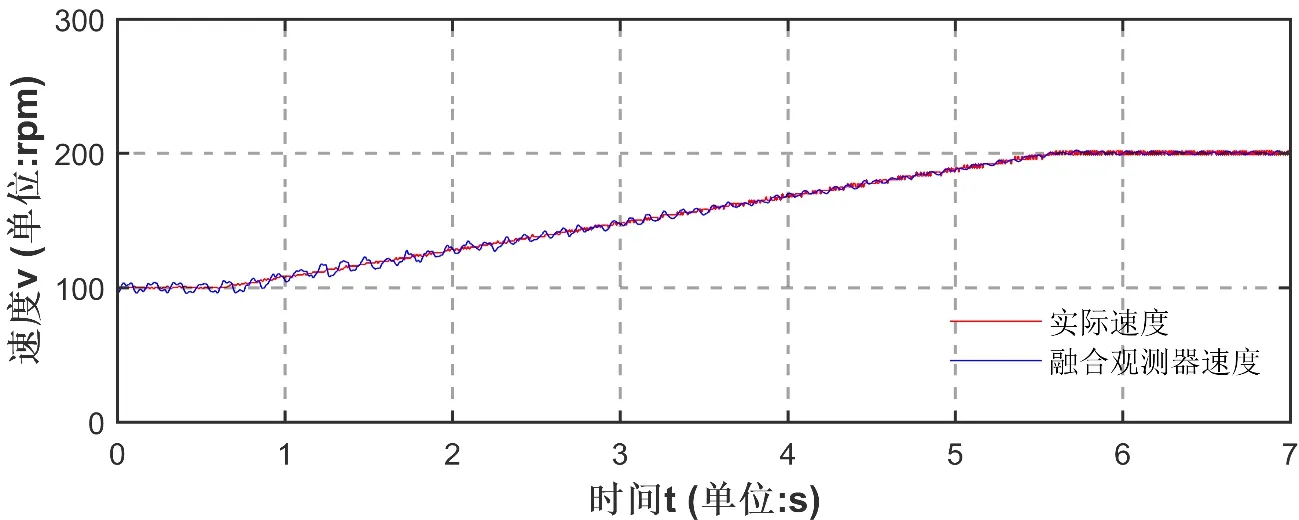
图12 升速过程中融合观测器速度跟踪波形Fig.12 Fusion observer speed result during a speed-up process

图13 升速过程中融合观测器角度跟踪波形Fig.13 Fusion observer position result during a speed-up process

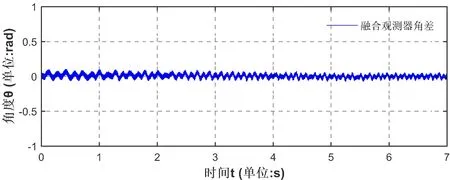
图14 升速过程中融合观测器角度跟踪波形Fig.14 Fusion observer position error during a speed-up process

6 结论

本文对同步磁阻电机角度估算方法进行了深入分析与讨论。对低速段的高频信号注入法存在的问题，及低速段与高速段不同估算方法间的融合问题进行了详细的分析，提出一种改进的高频反馈信号处理方法及改进的速度融合观测器方案。通过电机实验验证了改进高频信号处理方法的优越性，及融合速度观测器在切换角度估算方法过程中的稳定性和有效性，实验结果表明，本文提出的融合观测器具有跟踪误差更小、稳定性更好的特点。在未来的研究中，可着重关注同步磁阻电机电机在不同负载状态下，及在额定转速点以上运行时的位置估算问题，以将融合观测器适用的范围进行扩宽，提高方法的适用性。

[1] 蔡顺. 同步磁阻电机性能分析与结构优化[D]. 浙江：浙江大学, 2017.CAI Shun. Performance Analysis and Optimization of Synchronous Reluctance Machines[D]. Zhejiang：Zhejiang University, 2017.

[2] 符一凡, 向大为, 何志明. 一种无传感永磁电机效率自动跟踪控制方法[J]. 新型工业化, 2017, 7(7):5-13.FU Yi-fan, XIANG Da-wei, HE Zhi-ming. An automatic efficiency tracking control method for sensorless permanent magnet synchronous motor[J]. The Journal of New Industrialization, 2017, 7(7):5-13.

[3] YOUSEFI-TALOUKI A, PESCETTO P, PELLEGRINO G. Sensorless Direct Flux Vector Control of Synchronous Reluctance Motors Including Standstill, MTPA, and Flux Weakening[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3598-3608.

[4] LANDSMANN P, KENNEL R, KOCK H W D, et al. Fundamental saliency based encoderless control for reluctance synchronous machines[C]//The XIX International Conference on Electrical Machines, 2010: 1-7.

[5] ICHIKAWA S, TOMITAT M, DOKI S, et al. Sensorless control of synchronous reluctance motors based on an extended EMF model and initial position estimation[C]//Industrial Electronics Society, 2003. IECON ′03. The 29th Annual Conference of the IEEE, 2003(3): 2150-2155.

[6] TUOVINEN T, HINKKANEN M. Adaptive Full-Order Observer With High-Frequency Signal Injection for Synchronous Reluctance Motor Drives[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2):181-189.

[7] TUOVINEN T, HINKKANEN M, LUOMI J. Analysis and Design of a Position Observer With Resistance Adaptation for Synchronous Reluctance Motor Drives[J]. IEEE Transactions on Industry Applications, 2013, 49(1):66-73.

[8] 柏建勇, 刘雨佳. 基于MRAS观测器的PMSM无速度传感器模型预测电流控制[J]. 新型工业化, 2015, 5(9):52-58.BAI Jian-yong, LIU Yu-jia. Speed Sensorless Model Predictive Current Control for PMSM System Based on MRAS Observer[J]. The Journal of New Industrialization, 2015, 5(9):52-58.

[9] MORANDIN M, RU D D, BOLOGNANI S, et al. An Integrated Starter-Alternator Based on a Sensorless Synchronous Reluctance Machine Drive[C]//IEEE Vehicle Power and Propulsion Conference. IEEE, 2015:1-6.

[10] KILTHAU A, PACAS J M. Parameter-measurement and control of the synchronous reluctance machine including cross saturation[C]//Industry Applications Conference, 2001. Thirty-Sixth Ias Meeting. Conference Record of the. IEEE, 2001 , 4 (4): 2302-2309.

[11] TUOVINEN T, HINKKANEN M. Signal-Injection-Assisted Full-Order Observer With Parameter Adaptation for Synchronous Reluctance Motor Drives[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3392-3402.

[12] 王子辉. 永磁同步电机全速度范围无位置传感器控制策略研究[D]. 浙江：浙江大学, 2012.WANG Zi-hui. Research on the Position-Sensorless Control Strategy of PMSM at Full Speed Range[D]. Zhejiang: Zhejiang University, 2012.

[13] 张耀中. 永磁同步电机无位置传感器矢量控制系统的研究[D]. 浙江：浙江大学, 2015.ZHANG Yao-zhong. Research on Permanent Magnet Synchronous Motor Sensorless Vector Control System[D]. Zhejiang: ZhejiangUniversity, 2015.

[14] PAN P, LIU T, MADAWALA U K. Adaptive controller with an improved high-frequency injection technique for sensorless synchronous reluctance drive systems[J]. 2016, 10(4): 240-250.

[15] CONSOLI A, SCARCELLA G, SCELBA G, et al. Sensorless Rotor Position Estimation in Synchronous Reluctance Motors Exploiting a Flux Deviation Approach[J]. IEEE Transactions on Industry Applications, 2007, 43(5):1266-1273.

[16] KIM S, SUL S K, IDE K, et al. Maximum efficiency operation of Synchronous Reluctance Machine using signal injection[C]// Power Electronics Conference. IEEE, 2010:2000-2004.

[17] BUGSCH M, HELD A, PIEPENBREIER B. Sensorless control of SynRMs using an adaptive 2DoF current control including a comparison of two alternating HF signal injection-based methods[C]//Industrial Electronics Society, IECON 2016 -, Conference of the IEEE. IEEE,2016:2910-2916.

[18] JOVANOVIC M G, BETZ R E, PLATT D. Sensorless vector controller for a synchronous reluctance motor[C]//Ias Meeting, Ias ′96.Conference Record of the. IEEE, 1998(1): 122-129.

[19] BOLDEA I, PAICU M C, ANDREESCU G D. Active Flux Concept for Motion-Sensorless Unified AC Drives[J]. IEEE Transactions on Power Electronics, 2008, 23(5):2612-2618.

[20] 王君瑞, 马宏兴, 郭冀岭, 等. 异步电机矢量控制中死区补偿的仿真研究[J]. 电机与控制学报, 2006(2):164-170.WANG Jun-rui, MA Hong-xing, GUO Ji-ling, et al. Simulation of the dead-time compensation in vector-controlled induction motor[J].Electric Machines and Control, 2006(2): 164-170.