LBSN中融合线上关系和线下行为的好友推荐算法
丁 勇 曲秋菊 蒋翠清
(合肥工业大学管理学院 安徽 合肥 230000)
0 引 言
随着智能手机和社会化媒体的普及,基于位置的社交网络(LBSN)服务得到广泛应用,并在人们的社交生活中发挥重要作用。推荐与注册用户具有相似兴趣的朋友是LBSN最重要的服务之一。但是,社交网络中的海量信息必然造成信息过载的问题,在这种情况下,如何为用户推荐感兴趣的信息,成为学术界研究的热点[1]。
LBSN通过位置特征将社交空间和现实行为联系起来,融合了线下行为和线上关系。因此,基于LBSN的好友推荐特征的选取包含两方面:一是线下行为特征,具体包括签到时间、地点偏好、距离远近程度等;二是线上关系特征,即用户间的好友关系。在线下行为特征方面,Wu等[2]将用户在地点的签到信息按时间段进行划分,计算签到次数的相似性;俞菲等[3]采用核密度函数估算用户签到行为概率分布,用信息熵度量签到行为在时间上的集中程度;潘果等[4]将距离上小于300米的经纬度坐标为同一地点,计算待推荐用户与目标用户在同一地点的签到次数;Ying等[5]使用移动轨迹和文本内容计算相似性。在线上关系特征方面,Silva等[6]利用好友关系拓扑图进行好友推荐;Romero等[7]对用户的影响度排序,进行好友推荐;Wu等[2]基于随机游走算法进行好友关系的计算;李霞等[8]基于社交网络的拓扑结构和相邻点间的信任度构建推荐模型。
但是,上述研究中仍存在以下几点问题:第一,在计算位置相似性时往往将时间划分为几个时间段,分段进行相似度计算,那么两个用户在不同时间段于同一地点进行签到该如何考虑呢?第二,用户及其好友在签到距离上存在什么样的关系?第三,用户与待推荐用户间的熟识程度与哪些因素最为相关?基于上述问题,本文提出一种新的融合线上关系和线下行为的好友推荐方法,选取位置偏好相似性、距离相似性、熟识度三个特征,并通过Gowalla上的数据实验验证该算法的有效性。
1 位置偏好相似性计算
用户的签到信息包括:签到地点经纬度、签到时间。因此,考虑签到数据的时间和空间特征来定义用户之间的位置偏好相似性。
1.1 考虑时间因素的位置偏好相似性计算
考虑时间因素时,按照日常的工作生活规律,将用户签到时间划分K段:t1为工作日的工作时间(周一至周五上午9点至下午5点),t2为工作日的非工作时间,t3为周末。用户的所有签到地点构成签到地点集L={l1,l2,…,lN},则用户ui在时间tk于地点ln签到的次数为cikn,因此,用户ui在时间tk于地点ln签到的概率为:
(1)
用户ui在时间tk得到签到概率向量pik=(pik1,pik2,…,pikN)。若待推荐用户与目标用户在相同地点相同时间段内的签到概率相近,则可以认为他们对于该地点有相似的偏好。利用余弦相似性计算待推荐用户uj和目标用户ui的签到概率相似性:
SimLTk(ui,uj)=cos(pik,pjk)=
(2)
利用式(2)计算得到了用户间在不同时间段对位置偏好的相似性:SimLT1、SimLT2和SimLT3。取三个时间段相似性的平均值作为考虑时间因素的位置偏好相似性,计算如下:
(3)
1.2 排除时间因素的位置偏好相似性计算
若用户u1在时间段t1于地点l3签到2次,用户u2在时间段t3于地点l3签到5次,利用式(1)计算的相似性结果为0,但是显然用户u1、u2对于地点l3是有相似偏好的。因此,为了排除时间段划分导致的偏差,本文将用户在不同时间段的签到次数相加,得到地点签到概率为:
(4)
相应的地点签到概率向量为pi=(pi1,pi2,…,piN),利用余弦相似性计算结果为:
SimL(ui,uj)=cos(pi,pj)=
(5)
1.3 计算位置偏好相似性分值
结合上述内容,定义位置偏好相似性计算公式如下:
SimLocation(ui,uj)=λSimLT(ui,uj)+(1-λ)SimL(ui,uj)
(6)
式中:λ为调整参数。式(6)强调了时间对于用户签到偏好的影响。
2 位置偏好相似性计算
2.1 用户及其好友签到距离关系探究
为了探究用户和其好友的签到地点在距离上有什么联系,随机选取了数据集中的10个用户进行实验。以下使用ID号为0的用户说明,对ID号为0的用户及其所有好友的签到地点经纬度作散点图结果如图1所示。
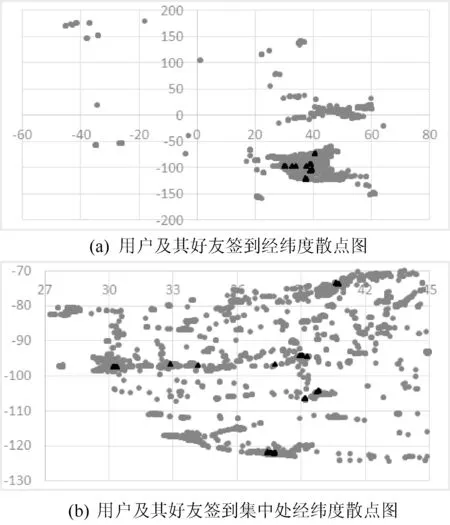
图1 用户及其好友签到经纬度散点图
图1中黑色的点为ID号为0的用户签到经纬度,其余点是其所有好友的签到经纬度。(a)是将(b)中签到集中部分放大后得出的,可以看出虽然用户0的好友签到范围非常广,但是在用户0签到过的地点周围却相对集中。
因此,得到以下结论:用户ui的好友签到地点集中分布在用户ui的签到地点附近。经过实验,用户ui的好友签到地点集中分布在用户ui的签到地点距离半径为20 km以内的地方。
2.2 计算距离相似性分值
获取目标用户ui的所有签到地点L(ui)={li1,li2,…,liM},待推荐用户uj的所有签到地点L(uj)={lj1,lj2,…,ljQ},则定义距离相似性计算公式如下:
(7)
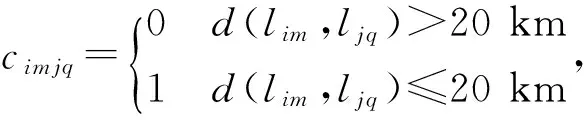
d(lim,ljq)=R·arccos[sin(latim)·sin(latjq)+
cos(latim)·cos(latjq)·cos(lonim-lonjq)]
(8)
式中:(latim,lonim)和(latjq,lonjq)是两地点的经纬度坐标;R为地球半径,近似为6 378 137米。
3 熟识度计算
假设网络中共有I个用户,用户间好友关系构成无向图G(U,E),其中ui∈U表示用户,(ui,uj)∈E表示用户ui和uj之间的好友关系。本文定义:
定义1用户ui和uj之间的最短连接路径所跨越的好友层次成为阶数。
定义2用户ui和uj之间拥有最短连接路径的路径数称为路数。
如图2所示,用户0和用户9的阶数为2,路数为3。
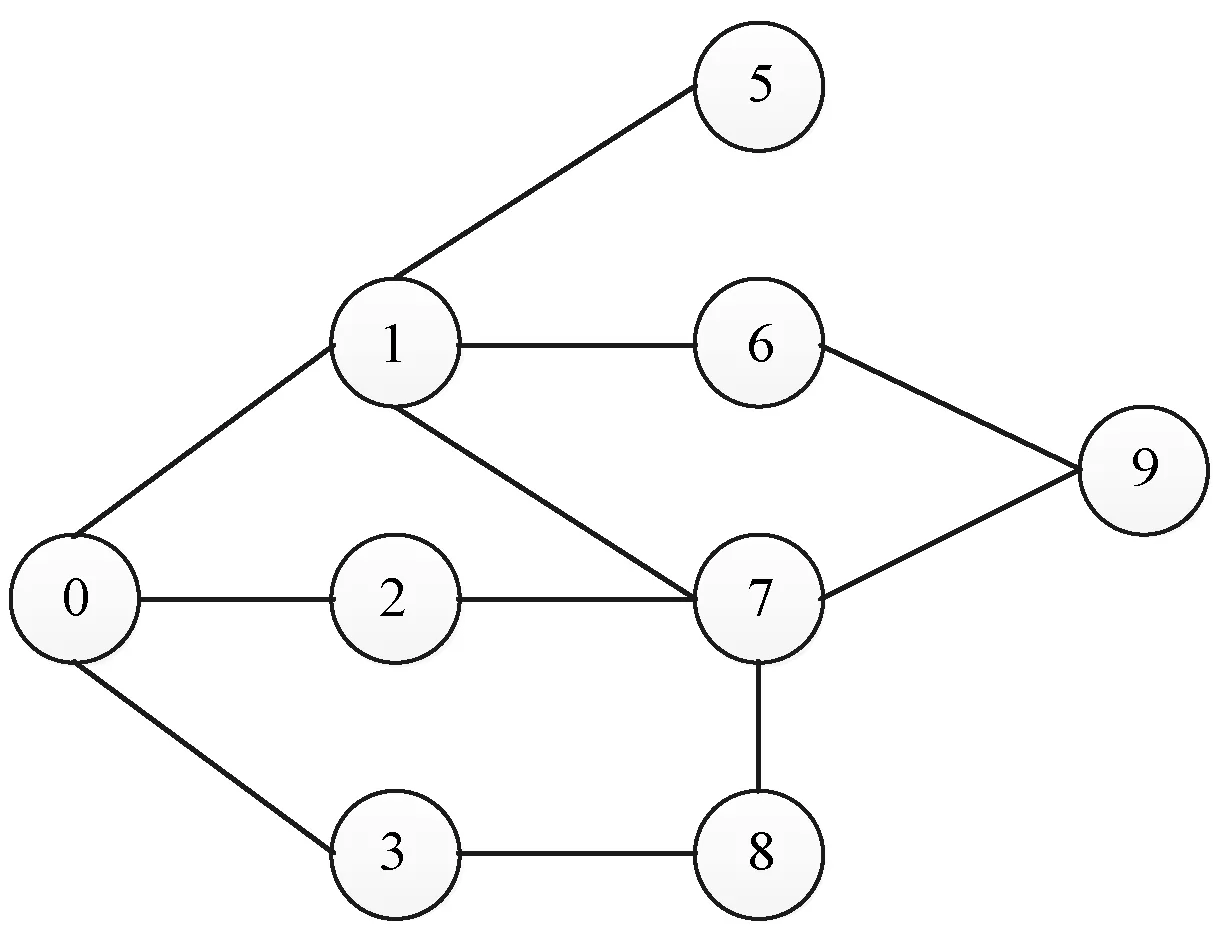
图2 好友关系图
传统的好友关系中只考虑了共同好友的数量对熟识度的影响,根据六度分隔理论,最多通过六个人你就能够认识任何一个陌生人,因此用户间的熟识度应考虑多层的关系。本文定义熟识度计算公式为:
SimFamiliarity(ui,uj)=βRankij×Routeij
(9)
式中:Rankij为用户ui和uj间的阶数,Routeij为用户ui和uj间的路数,β为小于1的参数。考虑到阶数对熟识度的影响比路数大,基于本文实验数据取β为0.001。
4 计算最终推荐分值
4.1 计算相似性分值
将上述三个特征进行集成,计算相似性分值。为保证加权有效,将三个特征值进行标准化处理:
(10)
最终计算公式为:
Sim(ui,uj)=ξSimLocation′+
ζSimDistance′+(1-ξ-ζ)SimFriend′
(11)
式中:Sim为相似性分数,ξ和ζ为调整参数,ξ,ζ∈[0,1];SimLocation′为位置偏好相似性标准化后的结果,SimDistance′为距离相似性标准化后的结果,SimFriend′为熟识度标准化的结果。
4.2 用户影响力
除了上述相似性对好友推荐产生影响之外,本文进一步考虑用户影响力对好友推荐的影响。用户影响力反映了用户在网络中的重要程度,网络中用户的行为往往会参考影响力高的用户的推荐意见。因此影响力高的用户在相似性相同的情况下更可能被加为好友。
本文使用好友数和签到次数衡量用户影响力,其中签到次数表现了用户主观发挥影响力的意愿,计算公式为:
Influencej=Cj×Hj
(12)
式中:Influencej为用户uj的用户影响力,Cj为用户uj的总签到次数,Hj为用户uj的好友总数。
4.3 最终推荐分值
将用户影响力根据式(10)进行标准化后与相似性融合,得到最终推荐分值:
(13)
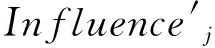
5 实验和分析
5.1 实验数据集和评价指标
本文实验选择Gowalla签到数据集[9]作为研究对象,数据集包含196 591个用户信息,6 442 892个签到记录,1 900 653对好友关系。由于数据稀疏性大,为保证实验的有效性,首先对数据进行预处理[10-11],剔除了签到次数小于20、好友数小于10的用户,从剩余的数据中随机选取1 052个用户进行实验,其中包含14 911个签到地点,361 513条签到记录,48 512对好友关系。数据构成的关系网络是全联通的,即任意两点是联通的,不存在孤立节点,且任意节点的度大于10。在用户的好友关系上随机选取80%的数据作为训练集,20%作为测试集进行实验。
本文选取准确率(precision)、召回率(recall)和F1-measure作为评价指标[12-13]:
5.2 实验设计与结果分析
5.2.1 对比实验
为验证算法的有效性,将本文提出的算法与文献[2-3]中的算法进行对比。本实验采用Top-N策略,将推荐值最高的用户推荐给目标用户,n选取5、10、15、20。本文中调整参数λ、ξ和ζ受实验数据的影响,因此需要根据具体数据进行调整。在本实验中λ取0.5,ξ和ζ取0.3,实验结果如图3所示。从图中可以看出,本文提出的好友推荐算法在准确率、召回率和F1-measure值三个评价指标上明显高于文献[2]和文献[3]中的算法。
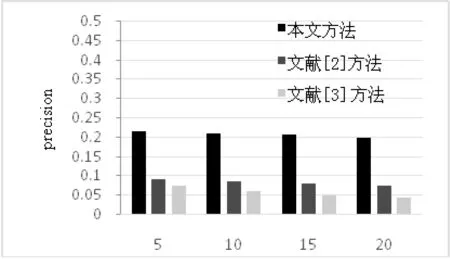
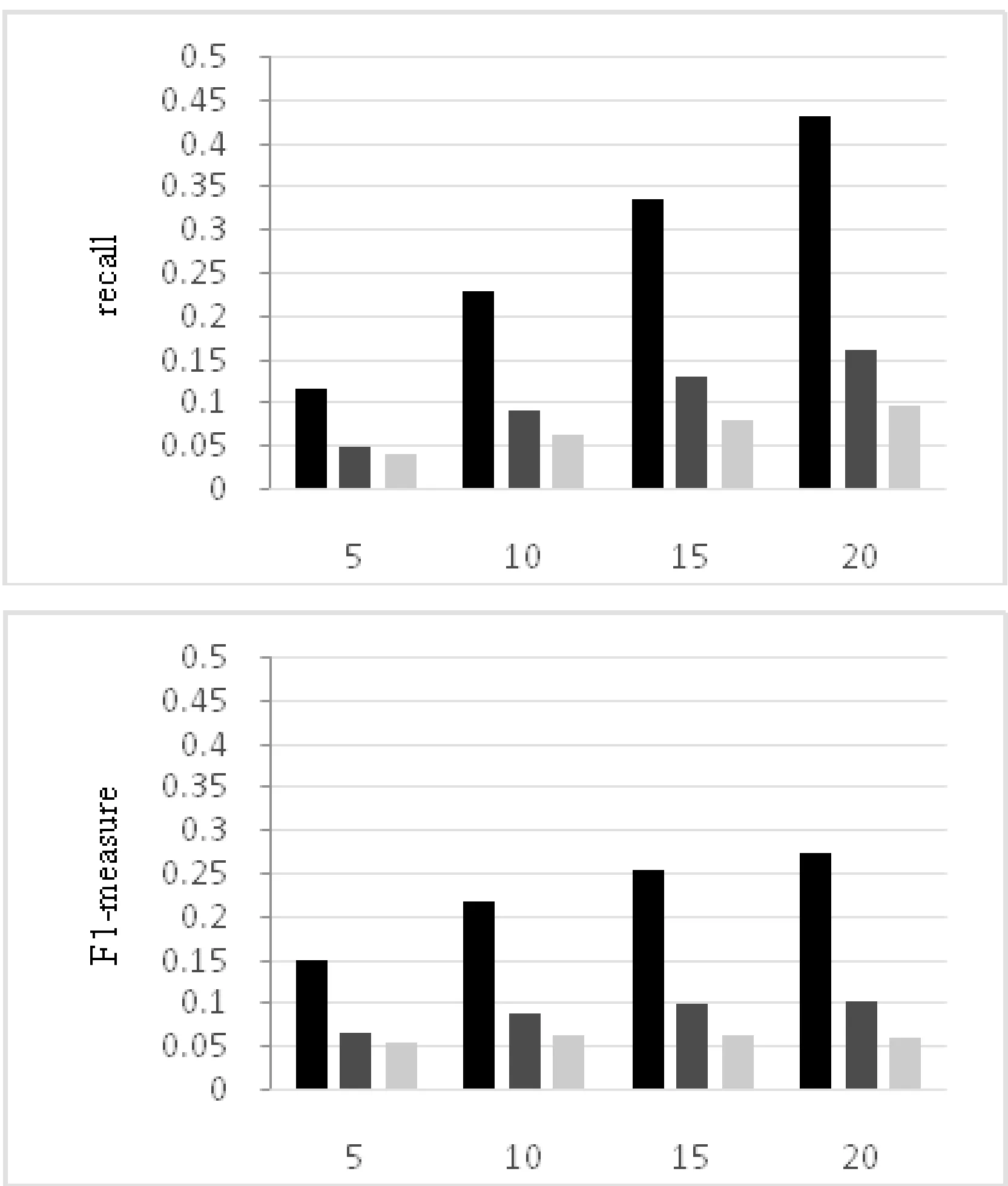
图3 各评价指标对比图
5.2.2 特征组合对性能的影响
本实验将各个特征性能与集成结果进行对比,进而观察各个特征对推荐效果的影响,实验结果如图4所示。从图中可以看出:首先,熟识度的各个指标远高于其他两个特征,这可能是由于数据的稀疏性造成的[14],高数据稀疏性使相似度计算的准确性降低,并且线上的好友关系是真实存在的,它对于用户间交友的影响更加直观。其次,随着推荐个数的增多,集成的准确率、召回率和F1-measure增多越来越不明显,但是仍高于某一单独特征,这是由于熟知度对推荐效果的影响远高于其他两点。
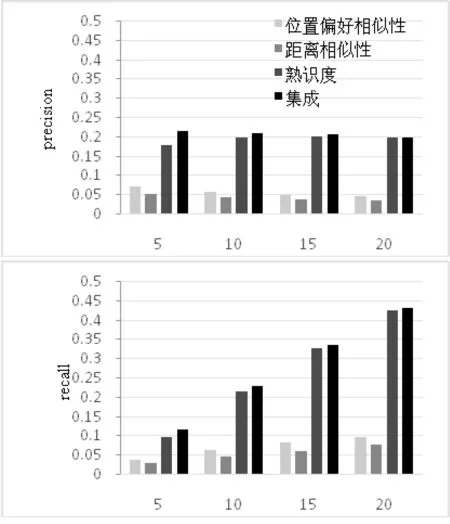
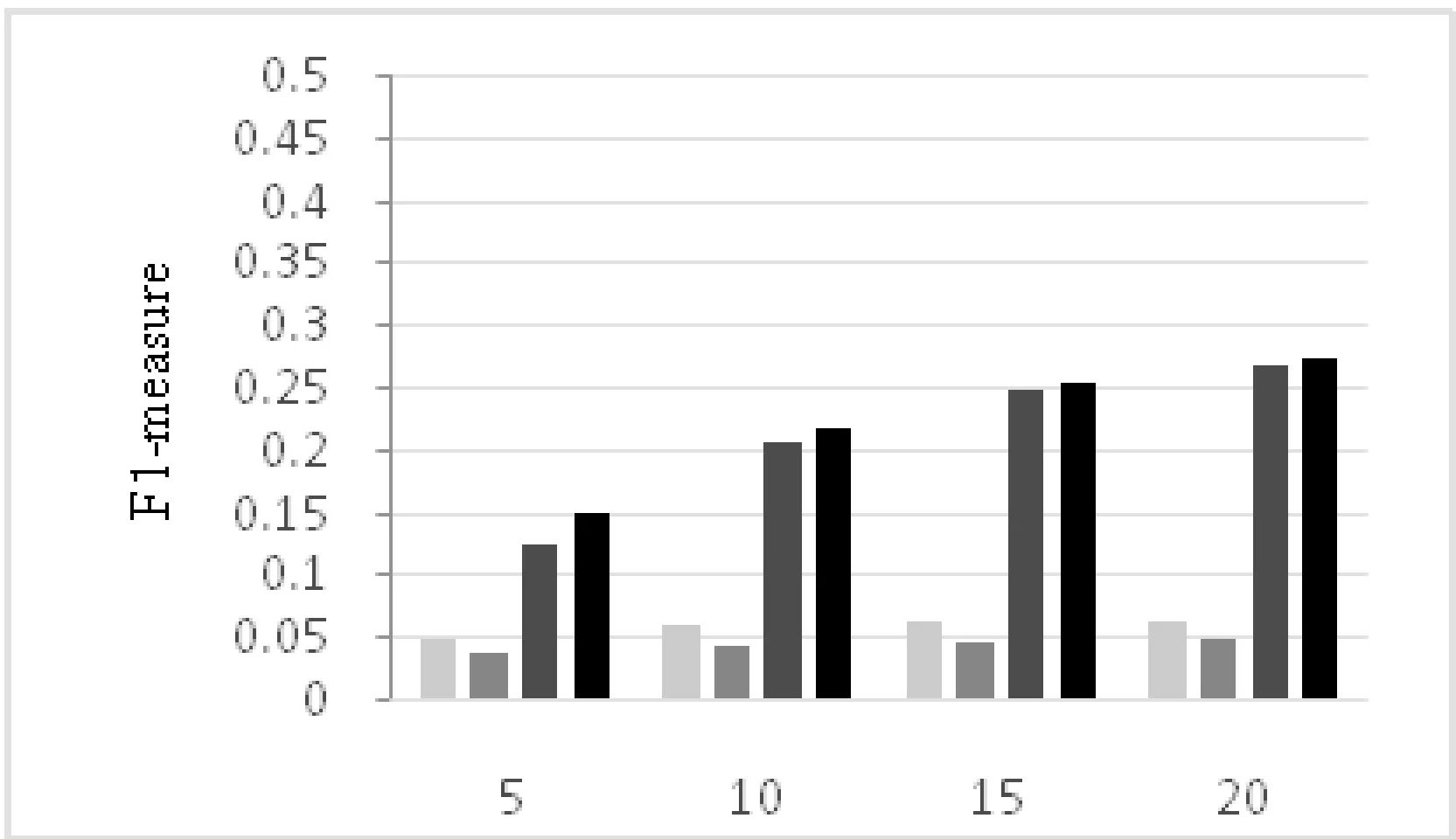
图4 特征组合的性能对比图
6 结 语
本文基于位置社交网络的签到信息以及好友关系,综合考虑位置偏好、距离相似性、熟识度三方面影响用户交友的因素,提出了新的融合线上关系与线下行为的好友推荐算法。算法将时间因素重新考虑到位置偏好的计算中,弥补了位置偏好计算中的不足;探究了用户及其好友的签到距离关系,定义了新的距离相似性算法;使用阶数和路数作为影响熟识度的因素,并定义了新的熟识度计算方法。最后将三个特征融合用户影响力进行赋值加权,并用对比实验验证了本文方法的有效性。在下一步的研究中,将考虑朋友圈的动态演化,同时在特征权重设置上考虑更为有效的方法。
[1] 杨阿祧, 汤庸, 王江斌,等. 基于博弈的社会网络个性化好友推荐算法研究[J]. 计算机科学, 2015, 42(9):191-194.
[2] Wu M, Wang Z, Sun H, et al. Friend Recommendation Algorithm for Online Social Networks Based on Location Preference[C]//International Conference on Information Science and Control Engineering. IEEE Computer Society, 2016:379-385.
[3] 俞菲, 李治军, 车楠,等. 一种面向获取空间信息的潜在好友推荐算法[J]. 软件学报, 2017, 28(8):2148-2160.
[4] 潘果, 徐雨明. LBSN中位置信息与网络拓扑相融合的好友预测[J]. 计算机科学, 2014, 41(9):115-118.
[5] Ying J C, Lu H C, Tseng V S. Followee recommendation in asymmetrical location-based social networks[C]//ACM Conference on Ubiquitous Computing. ACM, 2012:988-995.
[6] Silva N B, Tsang I R, Cavalcanti G D C, et al. A graph-based friend recommendation system using Genetic Algorithm[C]//2010 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2010:1-7.
[7] Romero D M, Galuba W, Asur S, et al. Influence and Passivity in Social Media[M]//Machine Learning and Knowledge Discovery in Databases. Springer Berlin Heidelberg, 2011.
[8] 李霞, 李守伟. 一种基于社交网络舆论影响的推荐算法[J]. 计算机应用与软件, 2017, 34(1):275-280.
[9] Cho E, Myers S A, Leskovec J. Friendship and mobility:user movement in location-based social networks[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, Ca, Usa, August. DBLP, 2011:1082-1090.
[10] 于亚新, 李玉龙, 刘欣,等. LBSNs中基于用户活动和社交信任的好友及位置推荐算法[J]. 小型微型计算机系统, 2014, 35(10):2262-2266.
[11] 蔡海尼, 陈程, 文俊浩,等. 基于用户签到和地理属性的个性化位置推荐算法研究[J]. 计算机科学, 2016, 43(12):163-167.
[12] 陈洁敏, 李建国, 汤非易,等. 融合“用户-项目-用户兴趣标签图”的协同好友推荐算法[J/OL]. 计算机科学与探索, 2017. CNKI 网络优先出版, 2017-02-20. http://www.cnki.net/kcms/detail/11.5602.TP.20170220.1008.008.html.
[13] 雷震, 吴玲达, 雷蕾,等. 一种基于构建-竞争聚类及KNNFL的事件探测与追踪系统[J]. 系统工程理论与实践, 2006, 26(3):68-74.
[14] Li X, Cong G, Li X L, et al. Rank-GeoFM: A Ranking based Geographical Factorization Method for Point of Interest Recommendation[C]//International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2015:433-442.

