一种基于不规则三角网的地层等值线绘制方法

段友祥 赵 琰* 孙歧峰 李洪强,2

1(中国石油大学(华东)计算机与通信工程学院 山东 青岛 266580) 2(中国石化集团胜利钻井工艺研究院 山东 东营 257000)

0 引 言

随着计算机图形学和科学计算可视化的发展，等值线的绘制也开始采用计算机自动生成，等值线的可视化研究一直受到人们的重视。在实际应用中，利用等值线可视化技术将地层离散的数据转换成连续的地形图像，使专业人员能够对地层构造形态做出正确的解释分析，确定石油富集区的位置、形态以及石油的储量等[1]。根据可视化的地层图像指导钻井作业，减少无效井位开采，不仅提高了寻找油气储藏的效率，而且具有重大的经济效益和社会效益。

传统的等值线追踪方法[2-5]大多是基于规则网格，其数据结构简单，便于存储管理，但数据冗余量大，效率不高。如周顺等[5]提出了基于规则三角网的等值线追踪算法，但这种算法比较适合于有规律的数据。当数据是不规则离散点时，需要利用二阶、三阶曲面方程等函数将数据拟合成有规则的曲面，插值完成后，将插值后的数据抽稀，再进行等值线追踪，这会导致等值线与实际的测量存在一定的误差。后来人们发展出了不规则网格，这种方法不仅适用于规则分布的离散数据点，避免了插值方法带来的精度损失，也适合不规则、甚至畸形分布的离散数据点。但也存在一些问题，如胡德鹏等[6]提出了基于不规则三角网的等值线追踪方法，在查找等值点时，不仅需要大量的存储空间来存储边界三角形、边界标识、已查找过的边、三角形等。而且，在追踪过程中需识别等值线穿过三角形的入口和出口，无形中增加了程序的复杂程度，生成的二维平面图形直观性相对较差。本文以某采油厂油藏等值线离散数据为基础，结合地层三维可视化的实际应用特点，针对传统等值线追踪方法的不足，提出了一种优化等值线绘制算法。该算法简化了传统方法中利用大量存储空间来存储边界三角形，已查找过的边、边界标识等元素的存储模式，将三角剖分后的数据进行有规律的存储及结构性处理，建立了相应的拓扑关系。不仅实现了地层等值线较高质量的绘制，而且提高了算法效率。

1 算法原理与相关数据结构

1.1 算法的基本思想

对于给定的油藏地层不规则离散点集合V={Xi,Yi,Zi},i=1,2,…,n，其中Xi和Yi为离散点的坐标，Zi为离散点的高程值，算法的原理如下：

1) 离散数据三角剖分。将离散数据通过逐点插入法生成不规则的三角网，并利用LOP算法不断对新生成的三角网进行优化。对于边界上多余的三角形，可通过限定三角形边的长度，对其进行适当的裁剪。

2) 求取等值点。根据给定的高程值，在生成的三角网上求取等值点。

3) 等值线追踪。利用简化后的数据结构，建立相应的拓扑关系，并根据等值线的不同类型分别进行等值线追踪，并对得到的等值线进行标注与平滑处理。

4) 等值线填充。获取所有的高程值数据，并将其映射为对应的色标，遍历整个三角网，将所有数据点进行任意形状填充。

1.2 数据结构

下面给出算法所需的数据结构定义：

1) 点的存储结构：

class Point

{

int ID;

//点的编号

double X;

//横坐标

double Y;

//纵坐标

double Z;

//高程值

listlist_ID_Edge;

//所属边的编号

listlist_ID_Tri;

//所属三角形的编号

}

2) 边的存储结构：

class Edge

{

int ID;

//边的编号

int ID_StartPoint;

//所属边的起点

int ID_EndPoint;

//所属边的终点

list list_ID_Tri;

//所属三角形的编号

}

3) 三角形的存储结构：

class Triangle

{

int ID;

//三角形的编号

int iEdgeIndex[3];

//三角形所包含的边编号

int iPointIndex[3];

//三角形所包含的顶点编号

}

4) 等值线存储结构：

class ContourLine

{

double d_Value;

//等值线所对应的属性值

ContourLineType conType;

//等值线类型

}

2 离散数据点的三维空间层面建模

不规则三角网TIN是数字高程模型DEM中最基本的表现形式，具有存储效率高、数据结构简单等优点。在TIN生成算法中，Delaunay三角剖分算法在地形拟合方面较普遍，常被用于TIN的生成。其算法总体上可以分为三类：三角网生长算法、逐点插入法和分治算法。三角网生长算法[7-9]出现较早，效率相对较低，目前采用较少；分治算法[10-11]效率高、时间复杂度小，但其使用大量递归算法，当数据量很大时，对计算机内存要求比较高；逐点插入算法[12-14]实现简单、效率高、占用内存较小，目前使用广泛。本文采用逐点插入法进行三角剖分。步骤如下：

1) 定义一个所有离散点的集合,并找到包含所有点集合的初始大三角形。

2) 在初始大三角形中建立初始三角网。插入一个数据点P，在三角网中找出包含P的三角形Tri，把P与三角形Tri的各个顶点相连生成三个新的三角形。

3) 用LOP算法将生成的三角网进行优化[15]，遍历所有的三角形，如有三角形的边在区域边界外，且超过给定的长度限制，删除该边界多余的三角形[16]。

以某采油厂地层离散数据为例，采取先将原始的三维离散点数据投影到二维平面，在二维平面内进行三角剖分，得到二维平面域内的剖分结果如图1所示。当平面域内的剖分算法完成后，将剖分后的结果映射回三维空间即可得到三维空间的层面模型。

图1 离散数据平面域内不规则三角剖分图

3 等值线追踪

3.1 等值点求取

要确定等值点在三角形边上的位置，首先要判断该边上是否有等值线穿过，如若存在，利用线性插值法计算得到等值点在平面区域上的位置坐标。设等值线的高程值为z，三角形边的两个端点的三维坐标分别为(x1,y1,z1)和(x2,y2,z2)，当高程值z的大小介于z1和z2之间时，证明该边上有等值线穿过，其判别式如下:

Δz=(z-z1)(z-z2)

(1)

式中：Δz表示高程判定值，z1和z2分别表示边的两个端点高程值。

当Δz<0时，证明等值线穿过该边(Δz=0时，另作讨论),反之，该边不存在等值线。图2显示了等值线的几种走向。其中，i、j、k表示三角形顶点，1、2、3表示三角形边。

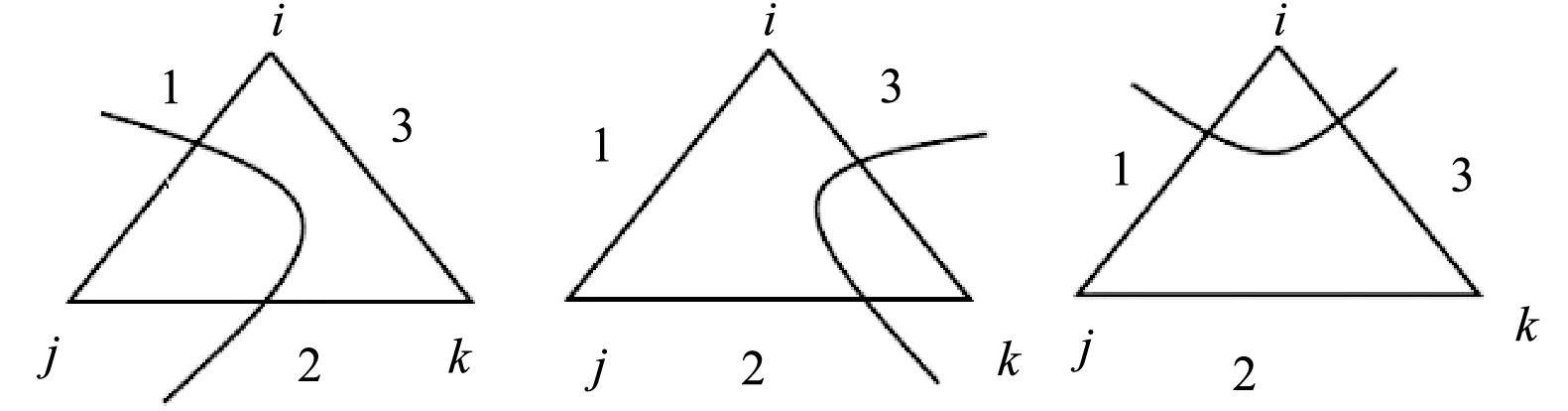
图2 等值线的走向示意图

找到某条边上的等值线后，求出该边上等值点在平面区域上的位置坐标。

其等值点的平面坐标如式(2)：

(2)

当Δz=0时，等值点经过三角形的顶点，对于这样的等值点，称之为奇异点。对于奇异点的处理参考文献[6]，对三角形顶点高程值加上(或减去)一个微小的正数ε的方法，其中ε>0,本文取ε=z×10-n,zi=z+ε,其中n=4，通过对奇异点的处理，极大地提高了等值线的精确性及拟合程度。

3.2 等值线追踪算法

得到Delaunay三角网上所有的等值点后，需要把高程值相同的等值点进行连接形成等值线。由于三角形公共边上的等值点，既是第一个三角形的出口点，又是相邻三角形的入口点，据此得到等值线追踪算法。

1) 非闭合等值线追踪，算法步骤如下：

① 以某个等值线数值为例，先在边界边链表list_EdgeBound中寻找一条等值边作为起始边，若存在，将该边记录到等值边list_ContourLine链表中，从搜索边链表中删除，否则，等值线闭合，执行2)。

② 查找以①中得到的起始边为边的三角形，遍历该三角形的其他边，查找其他的等值边，若存在，将其记录到等值边list_ContourLine链表中，同时，在搜索边链表删除。

③ 将该三角形从搜索三角形list_Tri链表中删除，以该三角形为基础搜索下一条等值边，若存在，将该边记录到list_ContourLine中，并在搜索边链表中把该等值边删除。

④ 循环③，如果查找到的等值边的最后一条是边界边链表中的边界边，非闭合等值线追踪完成。

2) 闭合等值线追踪，算法步骤如下：

① 以任意一条等值边作为起始边，若找不到这样的起始边，应开始另一条等值线的追踪。

② 查找以①中得到的起始边为边的三角形，遍历该三角形的其他边，查找其他的等值边，若存在，将该边记录到等值边list_ContourLine链表中，同时，在搜索边链表删除。

③ 将该三角形从搜索三角形list_Tri链表中删除，以该三角形为基础搜索下一条等值边，若存在，将该边记录到list_ContourLine中，同时，在搜索边链表删除。

④ 循环③，如果查找到的等值边是①中得到的起始边，闭合等值线追踪完成。

3) 循环执行1)、2)直到找到所有等值线对应的等值边系列。

图3是采用上述算法得到的地层高程等值线追踪图，达到了很好的等值线追踪效果。可以看出，优化的等值线追踪方法是对原有的等值线追踪方法进行了存储模式的简化。在三角剖分结束后，把三角剖分后的三角形数据有规律的存储，并针对每个三角形数据建立相应的拓扑关系，包括点、边、边界边等。通过共边数目来区分边界边，并将其保存在相应的链表中，在追踪非闭合等值线时，直接选取链表中数据作为起始边，极大地缩短了遍历时间。

图3 离散数据未平滑的等值线图

3.3 等值线平滑

追踪获得的曲线一般需要进行平滑处理。本文采用了抛物样条插值方法，对得到的等值线进行平滑处理。同时还可以根据需要，在等值线上添加标注以表明等值线的要素值。图3为未平滑加标注后的等值线图，图4为平滑加标注后的等值线图。从两图对比中可以看出，平滑后的等值线图质量更高。

图4 离散数据平滑后的等值线图

3.4 等值线图填充

填充是为了更好的可视化信息，例如用不同的颜色值代表不同的高程值，可以表示出地层的高低起伏状态，达到更真实的可视化效果。采用的基本方法是：将高程值转换为色标数据，然后通过一定的映射规则映射到特定的色谱上，即把高程值数据转换成不同的颜色，最后将这些颜色值以图像的形式显示出来(本文颜色均以灰度表示)。

1) 获得所有的高程值数据。

2) 定义色谱。颜色值通常用三原色(R,G,B)表示，即色标。若要生成可视化的图像，需要将高程值映射为相应的色标。在映射前首先需要定义一条用来映射的色谱，即一组颜色由浅到深的色标。色谱的选择与可视化的显示效果有着密切的关系，图5为本文所用的64个等级的色谱。

图5 64级色谱

3) 建立映射规则。建立映射规则是指确定高程值数据与RGB颜色值的对应关系。具体实现过程如下：

首先，找出所有高程值的最大值和最小值，分别表示为：Zmax、Zmin；其次，建立高程值和色标值的对应关系。假设色标的最大值和最小值分别为Cmax、Cmin，则高程值与色标对应关系由式(3)、式(4)和式(5)计算得到。

index=(Cmax-Cmin)/(Zmax-Zmin)

(3)

式中：index为色标转化系数。

C=Cmin-Zmin×index

(4)

式中：C为色标值变化量。

Ci=Zi×index+C

(5)

式中：Zi为某高程值，Ci为Zi高程值映射后得到的色标值。

4) 利用填充相关的操作生成可视化的地层图。遍历三角网，将所有的数据点进行任意形状的填充[17]。

图6为利用OpenSceneGraph库函数生成的可视化的地层图，图7为局部可视化地层图。

图6 可视化地层图

图7 局部地层图

在研究的基础上，选用具有高性能、可扩展、可移植等特点的OpenSceneGraph作为可视化实现平台，对地层等值线的三维可视化进行了实验验证。结果表明本文提出的基于优化不规则三角网等值线追踪算法的地层等值线绘制方法能够更加清晰逼真地反映地形概况，使全方位、多角度的地层观测分析方式变为可能，为随钻地质导向综合决策平台的实现奠定了基础。

4 算法精度分析与执行效率

本文算法实验环境为：Visual Studio2013+OpenSceneGraph。测试平台为：Windows 7中文旗舰版，Intel® CoreTM i5-3230M CPU 2.60 GHz， 4 GB 内存。

4.1 算法精度分析

等值线精度的影响因素主要为：离散数据的三角剖分以及等值线的平滑。首先，针对剖分方法而言，分为规则格网法及不规则三角网法。因规则格网法是通过拟合曲面插值产生的，所以插值后的数据较原来的离散数据丢失了精度。本文采用不规则三角网法，因地层数据相对密集，无需插值，由原始数据直接构成三角网，保持了原始数据的精度。其次，对于等值线的平滑方法而论，由于地层等值线是地质构造的基本表示形式，如果偏差一点，可能会造成一些精度损失，无法为专业人员提供正确的分析解释。为了确保等值线的精度，在平滑等值线时应尽量通过原始离散点。故本文选用抛物样条插值方法，使平滑后的等值线穿过所有原始点，减小了等值线平滑造成的精度损失，满足了地层等值线绘制的要求。

4.2 算法执行效率

为了考察本文追踪算法的实际执行效率和应用效果，选用不同规模的多组数据进行测试。离散数据点个数分别选择了200、1 000、5 000、10 000,4组实验数据，高程值个数都为10。表1为传统算法与改进算法的耗时对比。从表中可以看出改进后的算法时间性能大幅优于传统算法。

表1 传统算法与改进算法的耗时对比

5 结 语

本文针对现有的等值线追踪算法，提出了一个新的等值线追踪的解决方案。将原来复杂的存储模式进行了简化，在追踪之前对数据进行了结构性预处理，提高了等值线的追踪效率。该方法流程和结构简单，易于实现；利用抛物样条插值法实现了等值线的平滑操作；利用OpenSceneGraph实现了地层的三维可视化，专业人员能够比较容易地看到数据的变化趋势，满足了实际应用的需要。

[1] 韩丽娜.地质等值线图的生成与绘制[D].西安:西安科技大学,2006.

[2] 于嘉,吴旭.一种改进的矩形网格等值线追踪算法[J].河南师范大学学报(自然版),2008,36(6):34-36.

[3] 韦美雁,杜丹蕾.基于规则网格的等值线的生成研究[J].湖南科技学院学报,2007,28(4):39-41.

[4] 廖国忠,张伟,梁生贤,等.基于规则三角网的等值线追踪与填充算法的实现和应用[J].物探化探计算技术,2014,36(1):120-123.

[5] 周顺,李青元,张威,等.一种基于规则格网的等值线生成方法[J].测绘科学,2015,40(5):116-121.

[6] 胡德鹏,黄晓萍,任年海.基于不规则三角网(TIN)的追踪等值线算法及对等值线光滑算法的研究[J].计算机与信息技术,2006(3):46-48.

[7] Wu J Q,Xu A G.An improve method of Delaunay triangulated net growth algorithm[J].Science of Surveying & Mapping,2012,37(2):103-104，187.

[8] Chen Z Y,Fu J Z,Shen H Y,et al.An Improved Parallel Computation Method for Delaunay Triangulation[J].Advanced Materials Research,2013,819:299-303.

[9] Shamos M I,Hoey D.Closest-point problems[C]//16th Annual Symposium on Foundations of Computer Science.IEEE Computer Society,1975:151-162.

[10] Lewis B A,Robinson J S.Triangulation of planar regions with applications[J].Computer Journal,1978,21(4):324-332.

[11] 蒋红斐.基于分治算法构建Delaunay三角网的研究[J].计算机工程与应用,2003,39(16):81-82.

[12] 王龙浩,王解先.基于逐点插入法的Delaunay三角网快速生成算法[J].工程勘察,2013,41(10):75-79.

[13] 余代俊,蒲朝旭,朱逍贤.一种Delaunay三角剖分的改进算法[J].测绘通报,2014(6):51-54.

[14] 胡金虎.基于不规则三角网的高精度等值线生成方法[J].工程勘察,2011,39(2):64-68.

[15] 陈明晶,方源敏,李国柱,等.一种Delaunay三角网的改进生成算法[J].昆明理工大学学报(自然科学版),2016(5):33-38.

[16] 付晓东,赵俊三,马绍雄.不规则区域内基于D-TIN的等值线生成算法[J].昆明理工大学学报自然科学版,2006,31(6):46-50.

[17] 杨玺,吴晟,李英娜,等.基于不规则三角网的等值线填充算法[J].计算机应用与软件,2016,33(10):265-269.