非负矩阵MapReduce梯度下降半监督社区发现算法
赵 霞 魏霖静 肖 君
1(甘肃农业大学信息科学与技术学院 甘肃 兰州 730000) 2(甘肃省计算中心系统集成部 甘肃 兰州 730000)
0 引 言
复杂网络的构建方式是利用图形化方式实现对真实世界的描述,其特点是具有随机图拓扑结构特征。复杂网络中存在的主要问题是大数据,对大数据进行处理,可实现新功能的开发[1-2]。复杂网络分析时,如果事先知道其结构形式,则可较为简单实现对复杂网络的准确快速分析。复杂网络一般出现在生物、社会以及基础设施等不同网络中,通过社区结构开发,可实现信息共享、推荐以及分类等操作[3-4]。
目前,已开发出许多社区发现算法,例如,文献[5]提出基于模块度最大化方式的非重叠社区Newman贪婪计算方法,但是其仅考虑模块度,而未对模块密度指标进行考虑。文献[6] 提出基于Girvan算法的非重叠社区Newman检测算法,该方法是一种层次聚类的分裂计算方法。文献[7] 提出有向权重网络的信息论计算方法,用于对社区结构进行检测,通过信息流压缩网络优化,实现复杂网络社区的有效发现。文献[8]提出重叠社区形式下的信息传播策略,其对于唯一标签每个节点的搜索过程是有效的,但是算法并未对社区质量进行考虑。现实存在的复杂网络包含有大量的节点和边缘,上述算法在计算过程中并未考虑算法计算效率问题,因此对算法计算效率进行提升是研究的重点[9]。同时,上述提到的方法对于复杂网络的边缘密度指标非常敏感,容易受到这些指标的影响。上述算法并未考虑复杂网络结构间存在的交互力。
为实现复杂网络的快速分析,较为理想的社区检测方式是对计算效率和精度进行同步考虑。此外,需要在社区发现过程中充分考虑定向网络和权重网络等不同结构形式。对此,本文提出一种非负矩阵MapReduce梯度下降半监督社区发现算法,实验结果验证了算法的有效性。
1 问题描述
非负矩阵实质上是一类非常有效的低秩特征的模型逼近算法,可有效地实现异质网络的潜在多维信息的特征描述。当前,已有很多不同的社区数据挖掘算法,但是传统的社区矩阵发现算法需要将数据矩阵的因子F进行分解。同时施加正交形式的非负约束G,但是需要考虑到约束的强弱,太强容易造成逼近精度的下降,这会限制社区发现算法的逼近精度。为解决该问题,这里通过新矩阵S的引入,实现非负三重矩阵模型的构建:(1) 利用引入的光滑矩阵因子S,改善非负三重矩阵在执行分解过程中的自由度,提高分解精度;(2) 利用社区之间和之内存在的信息数据,提高联合聚类过程中流形约束性能;(3) 对迭代过程进行优化,并引入MapReduce算法实现算法计算效率的提升。
给定无向网络G,其包含n组节点数,并令复杂网络的特征矩阵形式为V=[Vij]n×n(Vij≥0),矩阵中的元素Vij含义是对节点i与j之间存在的相似度进行表征。利用非负矩阵的因子分解过程,可实现矩阵V利用Wn×k和Hk×n的近似分解,其中这两个分解矩阵是非负的,即Vn×n≈Wn×kHk×n。
采用非负矩阵方法进行社区发现的算法核心:特征矩阵V在进行分解操作后,获得的行向量v可视为列向量H的线性组合,形式为v=wH,其中参数w为矩阵W的行向量。对矩阵进行分解后,可获得具有更低维度的基向量H,实现对数据空间V的整体表示。参数w在公式中所起的作用是近似表达数据点v相对基向量的权重。利用矩阵W中所具有的行向量,对网络节点进行划分获得K个不同的类别,而矩阵W中的值则表达了网络节点相对于K个社区所具有的不同隶属度。图1为本文采用的非负矩阵社区发现算法的示例计算过程。

图1 基于非负矩阵分解社区发现示例
图1中(a)为网络模型中含有三组不同的社区模型,其中有两个简单网络包含重叠节点,分别是节点6和节点11。在对(a)网络模型进行非负矩阵操作后,可获得(b)的w分量归一化形式的社区结构的隶属度分布形式。根据曲线形式可知,(b)中的节点6和节点11的非负矩阵w分量在不同社区之间存在一定的交叉,这表明上述两个节点在两个社区之间都存在一定的关联,而非重叠节点仅在一个社区上呈现出较强的隶属特性。
2 半监督非负矩阵社区发现
2.1 算法描述

(1)
(1) 损失均方函数,一般是矩阵间所存在差异因子的Frobenius范数均方值,形式如下:
(2)
(2) 散度KL目标定义形式如下:
LKL(X,WHT)=KL(X‖WHT)
(3)
针对不同类型的程序可选择不同的目标进行表征,这里在网络约束中引入约束,构建对称框架形式。若复杂网络为无向链接类型,那么对于对称形式的邻接矩阵,其分解后所获得的结果也是对称形式的,那么得到的损失均方函数新的形式如下:
(4)
由于LLSE、LKL与LSYM相对矩阵W与H均具有非凸特性,因此在矩阵W与H均存在情形下,难以简单地使用启发式方法对损失函数进行优化,获得全局性的局部极小。同时,因为矩阵W与H,LLSE、LKL与LSYM相对于上述矩阵是具有凸性特征的,可利用迭代过程实现对LLSE的过程优化:
(5)
如迭代过程式(5)所示,LKL与LSYM可基于以下两组迭代过程进行优化更新:

(6)
(7)
复杂网络的社区发现,其将网络拓扑数据作为算法输入,数据形式可表达成邻接矩阵。在进行社区发现时,利用对目标的优化获得最小值,从而得到与邻接矩阵相关的新矩阵。然后,在新矩阵中对其执行分类过程。在以上定义指标基础上,复杂网络图的项Rβ(O,H)满足正则化特征,且有β∈{LSE,KL},该网络所具有拓扑信息目标如下:
Fα,β(H|X,Y)=Lα(X,H)+λRβ(Y,H)
(8)
式中:X∈{LSE,KL,SYM,MOD,ADJ,LAP,NLAP},λ为复杂网络先验和拓扑信息的均衡系数,该系数λ一般取正值。仅LADJ与LMOD内的第一项,系数λ取负值,原因是这些位置的术语目标取最大化,而其余术语目标取最小化。为简化社区发现,对于目标式(8)选取一致的距离目标。如果存在α∈{LSE,SYM,MOD,ADJ,LAP,NLAP},β=LSE;那么α=KL时,β=KL。由此可得目标形式为:
(9)
(10)
(11)
FMOD(H|X,Y)=-Tr(HTBH)+λTr(HTLH)
(12)
FLAP(H|X,Y)=Tr(HT(D-X)H)+λTr(HTLH)
(13)
2.2 Frobenius范数矩阵迹优化
2.1节节所提到的目标FLSE、FSYM和FKL对于矩阵H与W满足非凸性,利用一般的迭代优化,无法寻找到全局极值点,对此这里设计三种类型的更新优化策略,目的是寻找到其全局极值点:

FLSE(H|X,Y)=Tr((X-WHT)(X-WHT)T)+
λTr(HTLH)=Tr(XXT)+Tr(WHTHWT)-
2Tr(XHWT)+λTr(HTLH)
(14)
在W=[wij]≥0与H=[hij]≥0上分别利用ψ=[ψij]∈RN×K和Φ=[φij]∈RN×K两个拉格朗日乘子进行处理,可得LLSE形式如下:
LLSE=Tr(XXT)+Tr(WHTHWT)-2Tr(XHWT)+
λTr(HTLH)+Tr(ψWT)+Tr(ΦHT)
(15)
在给定矩阵H和W情况下,对LLSE求解最小值过程,可基于偏导求解获得:
(16)
(17)
因为ψikwik=0并结合Kuhn Tucker约束φjkhjk=0,可获得wik与hjk求解形式为:
-(XH)ikwik+(WHTH)ikwik=0
(18)
-(XTW)jkvjk+(HWTW)jkvjk+λ(LH)jkvjk=0
(19)
在上述基础上,可得下列目标更新策略:
(20)
如果λ=0,式(20)所示迭代规则即为式(5)迭代规则,上述迭代过程采用欧氏距离进行优化标准制定。采用类似方式,可获得求解LSYM最小值的迭代优化规则:
(21)
为确保一致性,可设λ″=2λ′。基于相同策略可对FKL最小化,其迭代规则为:
(22)
式中:I是尺寸为N×N的矩阵,是单位阵,hk是矩阵H第k列,形式如下:
(23)
3 并行化梯度下降求解
3.1 梯度下降
梯度下降(最速下降)是基于梯度概念实现优化过程加速的方法。方向导数与梯度之间存在一定的关系:方向导数最大值对应的方向即为梯度方向,方向导数在该点上的最大值即为梯度模[15]。该算法的优点是实现简单,具有较快的收敛速度,应用在复杂网络中具有先天优势。具体计算过程见算法1。
算法1社区发现梯度下降求解
1. 算法初始:取值范围随机初始为任意值
2. 迭代过程:
目标计算:
终止条件判断:函数值差小于设定终止阈值,那么停止循环迭代;否则继续执行;
社区分类更新:
3. 输出结果
3.2 MapReduce并行计算
对于复杂网络,更新策略式(20)中参数X与Y均是非常大的高维矩阵,且具有稀疏数据形式,可采用〈i,j,xij〉与〈i,j,yij〉所示的key-value对形式进行MapReduce并行格式储存。此外,因为存在k≪min(m,n),为实现矩阵H与W的矩阵并行相乘,以降低数据计算开销,可将矩阵H与W进行切割处理,获得n和m组具有k维尺寸行向量,即H=(h1,h2,…,hn)T及W=(w1,w2,…,wm)T,hi与wj均是具有k维尺寸的行向量,且迭代中均具有稀疏特性,可仅保存非零项。因此矩阵H与W也可基于〈i,hi〉与〈j,wj〉的key-value对形式进行MapReduce并行格式储存。更新策略式(20)进行分解计算,获得如下6个部分:P1=2XH,H←H⊕(P1+P2)⊗(P3+P4+P5),P2=YTW,P3=2HHTH,P4=HWTW,P5=αH+[β],每部分均可采用MapReduce进行并行计算,矩阵H各部分计算流可分别描述:
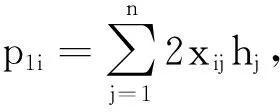

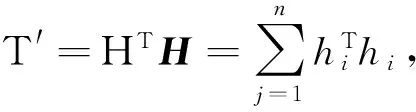
(4)P4=HWTW计算。与P3计算过程类似,先对T″=WTW执行计算,然后对P4=2HT″执行计算,T″与P4计算均仅需1组MapReduce操作执行:Map-7、Reduce-7、Map-8和Reduce-8,具体操作过程与前述P3操作相似,不再赘述。
(5)P5=αH+[β]计算。对于P5计算仅需一组MapReduce操作进行:Map-9和Reduce-9,其中在Map-9过程中,对元组〈i,hi〉进行读入,而在Reduce-9操作后获得元组〈i,αhi+[β]i〉,并输出。

3.3 复杂度分析
us范数计算中,因为涉及到社区数K=N,则每步的迭代需要执行的浮点运算数为O(N2K),因此上述算法计算过程并未增加矩阵分解计算复杂度。同时,因为邻接矩阵A满足稀疏特性,迭代过程所需的复杂度进一步降低到O((NK+M+R)K),R是先验连接点信息数。与此同时,基于KL散度迭代更新过程,所需的矩阵尺寸为N×N,需要执行的浮点运算数为O(N3)。

O(N2K+q(p+4)NK)=O((N+q(p+4))NK)
(24)
基于以上的复杂度分析,可知社区的Frobenius范数求解,适合用于复杂网络场景,其与网络规模N之间更接近于线性关系。那么采用MapReduce并行计算后,相应的计算复杂度应该除以并行数即可,计算效率得到大幅提升。
4 实验分析
选择测试集如下:Karate Club(KC)、Dolphin Network(DN)、Enron、DBLP、Amazon、Wikivote、American College Football(ACF)等。对比社区发现策略选取分层聚类算法(CNM)以及生成树算法(STA)。评价指标选取如下:准确度指标、召回指标、计算效率、模块度、模块密度、覆盖率等指标。准确度指标和召回指标计算形式如下:

(25)
准确度指标和召回指标分别从正确性和全面性两个角度对社区发现质量进行评价。表1所示为准确度指标和召回指标对比数据。

表1 准确度指标和召回指标
据表1实验数据,相对准确度指标,本文算法在测试网络中性能表现要比CNM以及STA社区发现算法更好。社区发现的准确度可达到90%,STA算法为85%左右,性能其次,CNM算法为72%左右,性能最差。在召回指标中,本文算法指标值可达89%左右,CNM算法可达87%左右,STA算法可达85%左右,本文算法具有更佳的计算性能。
图2所示是在覆盖率和计算效率两项指标上的实验对比结果,对比算法仍选取CNM以及STA社区发现算法。

图2 覆盖率和计算效率
根据图2所示对比曲线,在ACF、DBLP、KC、Enron四个测试网络上的覆盖率数据要显著比CNM以及STA社区发现算法更好。而在计算用时指标上,CNM和STA两种类型的社区发现过程用时较为接近,本文算法因为采用MapReduce并行执行策略,其计算速度明显更快。
最后以Amazon网络为对象进行模块密度和模块度两项指标的测试,见图3。

图3 Amazon基准测试
根据图3所示实验曲线,在Amazon网络上,本文算法在模块密度和模块度两项指标上均比CNM以及STA社区发现算法更好。其中,CNM社区发现结果的模块密度结果比STA社区发现结果更好,而STA社区发现结果在模块度上结果比CNM社区发现结果更好。
5 结 语
本文提出一种非负矩阵MapReduce梯度下降半监督社区发现算法,构建社区发现的矩阵迹优化规则,利用梯度下降法对社区非负矩阵进行求解,并构建基于MapReduce的并行计算方式,仿真实验验证了算法有效性。下一步研究方向:(1) 构建真实数据集对算法性能进行测试;(2) 对算法的并行计算过程进行优化,考虑采用其他形式的并行计算框架;(3) 对梯度下降算法进行研究,进一步提升算法性能,提高计算效率。
[1] 陈克寒,韩盼盼,吴健.基于用户聚类的异构社交网络推荐算法[J].计算机学报,2013,36(2):349-358.
[2] Guo Tao,Zhang Guo,Guo Wenjuan.An improved weighted complex network clustering method[J].Computer science,2012,39(6):99-102.
[3] 宣善立,梁栋,朱明,等.一种基于修正的最小生成树及其邻接谱的特征匹配算法[J].电子学报,2010,38(2):269-274.
[4] Jin Di,Liu Jie,Yang Bo.Large scale complex network community detection based on local search and genetic algorithm[J].Journal of automation,2011,37(7):873-881.
[5] Chen M,Nguyen T,Szymanski B.On measuring the quality of a network community structure[J].Social computing (SocialCom),2013,52(3):122-127.
[6] Zhang Xinmeng,Jiang Shengyi.Complex network partitioning algorithm based on incremental clustering of core graph[J].Journal of automation,2013,39(7):1117-1124.
[7] Wang T,Krim H,Viniotis Y.A Generalized Markov Graph Model:Application to Social Network Analysis[J].IEEE Journal of Selected Topics in Signal Processing,2013,7(2):318-332.
[8] Wang S S,Chern A,Tsao Y,et al.Wavelet Speech Enhancement Based on Nonnegative Matrix Factorization[J].IEEE Signal Processing Letters,2016,23(8):1101-1105.
[9] Venkataraman A,Yang D Y,Pelphrey K A,et al.Bayesian Community Detection in the Space of Group-Level Functional Differences[J].IEEE Transactions on Medical Imaging,2016,35(8):1866-1882.
[10] Karimi-Majd A M,Fathian M,Amiri B.A hybrid artificial immune network for detecting communities in complex networks[J].Computing,2015,97(5):483-507.
[11] Chen W H,Paik I,Hung P C K.Constructing a Global Social Service Network for Better Quality of Web Service Discovery[J].IEEE Transactions on Services Computing,2015,8(2):284-298.
[12] 刘衍珩,李飞鹏,孙鑫.基于信息传播的社交网络拓扑模型[J].通信学报,2013,34(4):1-9.
[13] Xie J,Szymanski B K.Towards linear time overlapping community detection in social networks[J].Lecture notes in computer science,2012,73(1):25-36.
[14] Qi Lilei,Zhao Dandan.Study on Optimization of urban public traffic system based on complex network[J].Journal of Southwestern Normal University (Natural Science Edition),2014,39(7):102-106.
[15] Hu Xiping,Li Xitong,Ngai E C.Multidimensional context-aware social network architecture for mobile crowdsensing[J].IEEE Communications Magazine,2014,52(6):78-87.

