基于状态机的递归算法非递归化框架

杨 硕 周霜菊 张志杰

1(沈阳化工大学计算机科学与技术学院 辽宁 沈阳 110142) 2(成都大学美术与影视学院 四川 成都 610106) 3(西南民族大学计算机科学与技术学院 四川 成都 610041)

0 引 言

递归程序具有代码简洁，易于理解的特点，其正确性也很容易得到证明，许多算法可以根据递推公式或递归定义直接写为递归函数[1]。常见的明显带有递归性质的算法问题，如：汉诺塔、阿克曼函数、N后问题等，如果直接用非递归程序表达，算法的编写难度会很大。因此，对于这类算法，程序员一般选择递归程序表达。但是，递归程序具有几个明显的缺点，使对其的非递归化研究成为必要：

(1) 低级编程语言(如汇编语言等)和某些早期的高级编程语言(如Coq、Agda等)不支持递归调用。

(2) 递归程序消耗较多的栈内存，当栈内存被耗尽时，会出现“栈内存溢出”的严重错误。栈内存的效率较高，函数发生调用时，函数中形参、局部变量和返回地址等的保存都需要栈内存。但是，x86计算机的栈内存只有1 MB，当递归深度较深时，会将栈内存耗尽，从而引起程序崩溃。而将递归程序非递归化后，可以利用malloc或new等函数从堆内存中获取容量大得多的动态内存，从而避免了栈内存耗尽的问题。

(3) 递归程序在频繁调用自身时，程序内部的参数和变量会不断地通过栈内存保存和恢复，这个过程会影响到函数的执行效率。

因为以上缺点，在某些情况下，程序员会将递归程序转化为非递归程序运行。常见的非递归化思路可以分为以下几种：

(1) 某些尾递归程序可以用递推迭代的方式非递归化[2-3]。典型的可以通过递推迭代非递归化的问题有阶乘算法和菲波那契算法等。

(2) 形式推导方法[3-7]。用数学方法推导出递归问题的本质，这种方式能够获得效率较高的非递归算法，如，利用下列公式，可以直接获得菲波那契序列的第n项值：

(1)

(3) 用栈模拟递归[8-11]。函数调用过程的本质实际上就是相关参数和数据的入栈和出栈的过程，因此，可以用栈模拟的方法将任意递归程序非递归化。该方法通用性强，有助于对递归问题本质的分析，但仅能解决栈溢出问题，对运行效率的提高帮助不大。根据编译器处理递归程序的机制可知：使用栈模拟方式的非递归程序中，栈中保存了初次调用到当前递归点的完整路径。

本文提出一种使用栈模拟的递归程序非递归化框架，与文献[9-11]中提到的“while-while”、“while-if”、“do-while”、“do-if”等形式不同的是：本文基于状态机编程的思想，将函数的调用过程分解为若干个状态。用栈和状态之间的条件转换模拟递归函数的调用过程，并提出一系列转换规则，使得递归程序的非递归化过程更加简便和程序化。

1 有限状态机和非递归化框架

1.1 有限状态机

有限状态机FSM(Finite State Machine)的思想最初来源于硬件控制电路。它把复杂的控制逻辑分解成有限个稳定状态，同时有限状态机也是软件上常用的一种基于数据驱动的处理方法。特别是在嵌入式系统的设计上，很多时序问题和实时事件的处理都可以借助有限状态机的思想解决。简单的有限状态机可以简化为两个要素组成：状态和条件。下一个状态的跳转取决于当前所处的状态以及发生的条件，即：下一状态=<当前状态，条件>。使用状态机编程思想可以让程序的复杂行为变得简洁透明，图1是一个典型的控制吸油烟机动作的有限状态机和控制代码。

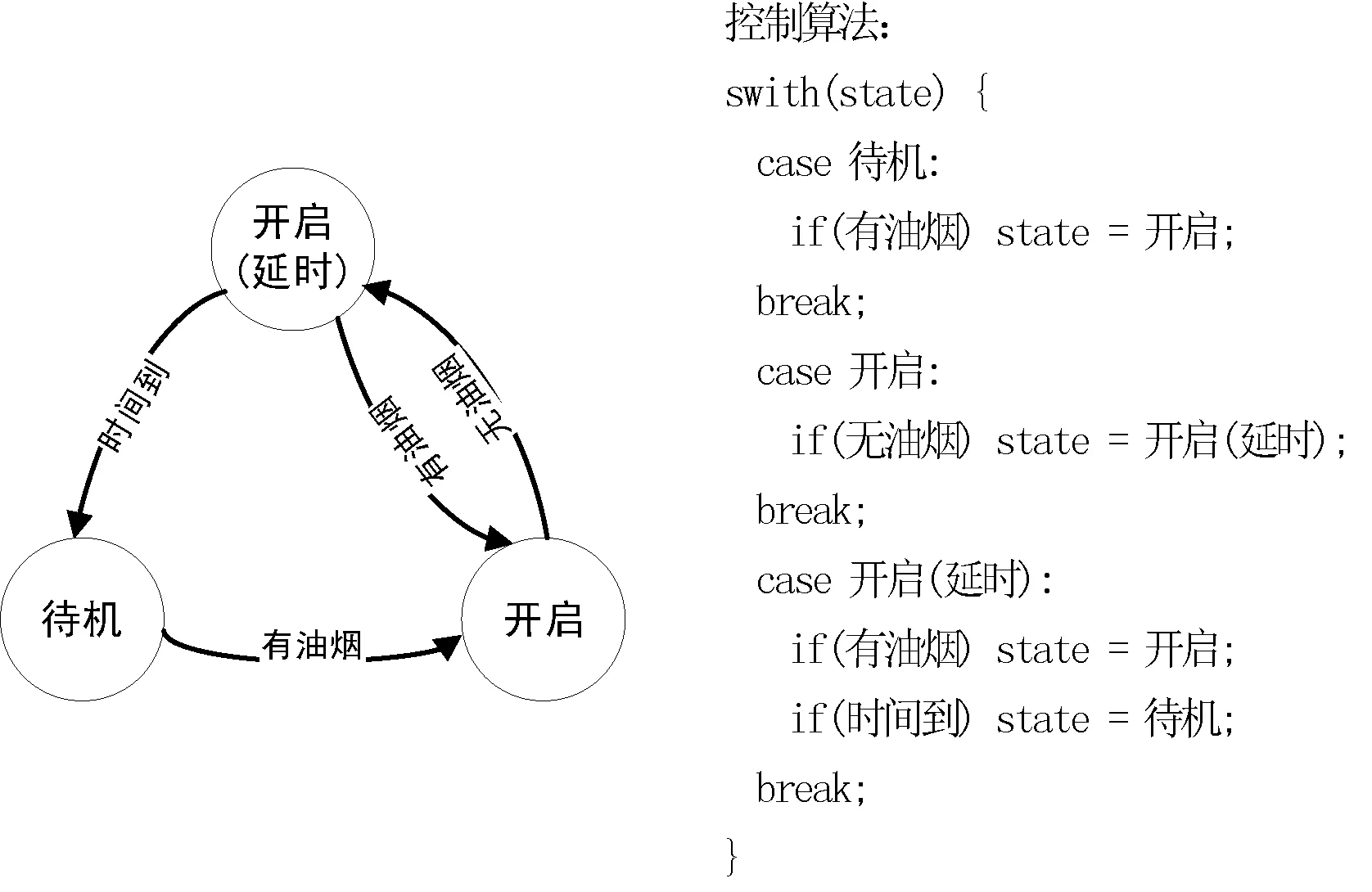
图1 典型的有限状态机和控制算法

1.2 递归到非递归的框架

以汉诺塔的递归程序为例，见算法1。在Hanoi函数内部一共发生了两次递归调用，因此，其函数调用关系树为一棵二叉树，图2为该二叉树的局部。

算法1汉诺塔的递归程序

void Hanoi(int n, char x, char y, char z) {

if(n == 1) move(x, 1, z);

//语句1，递归停止条件

else {

Hanoi(n-1, x, z, y);

//递归点1

move(x, n, z);

//语句2

Hanoi(n-1, y, x, z);

//递归点2

}

}

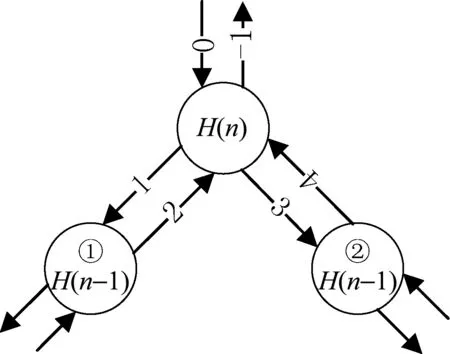
图2 Hanoi函数调用状态编码

图2中，H(n)表示参数为n的函数调用，两个H(n-1)表示在H(n)内部的两次递归调用。借助状态机的思想，对调用过程编码如下：

0：进入函数； 3：进入递归点2；

1：进入递归点1； 4：从递归点2返回；

2：从递归点1返回； -1：函数返回。

因此，对于形似Hanoi算法的递归函数，其非递归化状态机可以写为如算法2形式。其中，push表示发生一次函数调用并将相关参数和变量入栈保存，pop表示函数返回, state表示不同的调用状态。

算法2递归到非递归转换框架(形似Hanoi算法)

push();

while(栈不空) {

if(达到递归停止条件) {

pop();

}else if(state == 0) {

//进入函数

state = 1;

}else if(state == 1) {

//进入递归点1

state = 2;

push();

}else if(state == 2) {

//递归点1返回

state = 3;

}else if(state == 3) {

//进入递归点2

state = 4;

push();

}else if(state == 4) {

//递归点2返回

state = -1;

}else if(state == -1) {

//退出函数

pop();

}

}

算法2是本文提出的非递归化框架，非递归化时，只需将原递归程序中相关语句放置在算法2的相应状态中去即可。但是，算法2中存在一些状态的冗余，这些冗余状态可以以一定规则合并从而提高运行效率。为了去除状态冗余以及处理函数返回值等问题，本文提出了4个转换规则，其中：规则1、规则3用于去除冗余，提高效率，规则2用于栈的设计，而规则4处理函数返回值问题。

规则1递归函数从最后一个递归调用点返回后，将退出递归函数或返回到上一层，因此，可以去除算法4中的state == -1状态，并将其合并到state== 4处。对状态的精简可以提高非递归函数效率。

将算法2得到的框架推广并考虑到规则1，可以得到更为通用的转换框架，见算法3。

算法3递归到非递归转换框架(通用形式)

push();

while(栈不空) {

if(达到递归停止条件) {

pop();

}else if(state == 0) {

//进入函数

state = 2*i-1;

}else if(state == 2*i-1) {

//进入递归点i

state = 2*i+2;

push();

}else if(state == 2*i) {

//递归点i返回

if(当前为最后一个递归点) pop();

else state = 2*(i+1)-1;

}else if(state == 2*(i+1)-1) {…

//进入递归点i+1……

}

规则2栈的设计，栈中除了必须保存state状态变量外，依照编译器处理函数调用的流程，还需要保存以下3类参数和变量：1) 在递归调用过程中发生变化的函数形参，大多数递归函数需要保存所有的形参；2) 递归函数本身和递归点的返回值，如：保存递归函数本身的返回值re，递归点x的返回值rex；3) 递归函数中，影响递归调用的局部变量，这类变量决定了递归点的进入和返回。

2 常见递归算法的非递归化

2.1 汉诺塔程序非递归化

根据规则2，栈的设计如下：

(1) 发生变化的形参：n,x,y,z；

(2) 函数返回值：无；

(3) 影响递归调用的局部变量：无。

因此，栈的定义为：

struct {

int state;

//状态

int n;

char x, y, z;

}stack [MAXSIZE];

int ptop = -1;

//栈顶指针

此外，栈的功能函数定义为：push入栈，pop出栈，empty判断栈空，top获得栈顶。

在push函数中，state被自动初始化为0。

算法4为汉诺塔的非递归程序。

算法4汉诺塔的非递归程序

void HanoiS(int n, char x, char y, char z) {

push(n, x, y, z);

//state在push中被初始化为0

while(!empty()) {

//栈不空

if(top.n == 1) {

//递归停止条件

move(x, 1, z);

//语句1

pop();

//函数返回

}else if(top.state == 0) {

//进入函数

top.state = 1;

}else if(top.state == 1) {

//进入递归点1

top.state = 2;

push(top.n-1, top.x, top.z, top.y);

}else if(top.state == 2) {

//递归点1返回

top.state = 3;

move(x, n, z);

//语句2

}else if(top.state == 3) {

//进入递归点2

top.state = 4;

push(top.n-1, top.y, top.x,top.z);

}else if(top.state == 4) {

//递归点2返回

pop();

//函数返回

}

}

}

算法4中，语句1放置在递归停止条件内，语句2在左枝(第1个递归调用点)返回后被执行，因此放在状态2中。另外，语句2也可以放在状态3中，如此，状态2将成为多余状态(因为状态2中仅进行了状态的改变)，并在下一循环中直接跳到状态3。类似地，状态0也属于多余状态。因此，提出转换规则3去除多余状态。

规则3(状态合并规则) 如果某个状态中没有发生递归函数的调用(push)或退出(pop)动作，那么该状态可以与下一个状态合并。或者：每个状态下仅能包含一个push或pop操作，不包含任何push或pop操作的状态可以与下一个包含push或pop操作的状态合并。

根据规则3，算法4中，状态0和1可以合并，状态2和3可以合并，简化后的算法见算法5。

算法5汉诺塔的非递归程序(简化)

void HanoiS(int n, char x, char y, char z) {

push(n, x, y, z);

while(!empty()) {

if(top.n == 1) {

//递归停止条件

move(x, 1, z);

//语句1

pop();

//函数返回

}else if(top.state == 0) {

//进入函数,进入递归点1

top.state = 1;

push(top.n-1, top.x, top.z, top.y);

}else if(top.state == 1) {

//递归点1返回,进入递归点2

top.state = 2;

move(x, n, z);

//语句2

push(top.n-1, top.y, top.x,top.z);

}else if(top.state == 2) {

//递归点2返回

pop();

//函数返回

}

}

}

2.2 Pnx函数(带有返回值)非递归化

Pnx函数递归程序见算法6。

算法6Pnx递归程序

int Pnx(int n, int x) {

if(n == 0) return 1;

if(n == 1) return 2*x;

return 2*x*Pnx(n-1,x) - 2*(n-1)*Pnx(n-2,x);

}

Pnx函数类似于菲波那契算法，实际上可以通过递推迭代解决。Pnx函数的递归点位于表达式中，首先整理表达式，将递归点独立出来，见算法7。

算法7Pnx递归程序(整理)

int Pnx(int n, int x) {

int re, re1, re2;

if(n == 0) re = 1;

//递归停止条件

else if(n == 1) re = 2*x;

//递归停止条件

else {

re1 = Pnx(n-1, x);

//语句1,递归点1

re2 = Pnx(n-2, x);

//语句2,递归点2

re = 2*x*re1 - 2*(n-1)*re2;

//语句3

}

return re;

}

根据规则2，栈的设计如下：

(1) 发生变化的形参：n(x在调用中未发生变化)；

(2) 函数返回值：re，re1，re2；

(3) 影响递归调用的局部变量：无。

Pnx函数的递归调用次序与Hanoi函数完全一致，经过规则3化简后，Pnx的非递归程序见算法8。

算法8Pnx非递归程序(简化)

int PnxS(int n, int x) {

push(n);

while(!empty()) {

if(top.n <= 1) {

//递归停止条件

if(top.n == 0) top.re = 1;

if(top.n == 1) top.re = 2*x;

pop();

//函数返回

}else if(top.state == 0) {

//进入函数,进入递归点1

top.state = 1;

push(top.n - 1);

}else if(top.state == 1) {

//递归点1返回,进入递归点2

top.state = 2;

top.re1 = uptop.re;

//语句1

push(top.n - 2);

}else if(top.state == 2) {

//递归点2返回

top.re2 = uptop.re;

//语句2

top.re = 2*x*top.re1 - 2*(top.n-1)*top.re2;

//语句3

pop();

//函数返回

}

}

return stack[0].re;

}

算法8中，uptop为栈顶的下一个位置(令top为stack[ptop]，则uptop为stack[ptop+1])。对于基于栈模拟的非递归化算法，栈中保存了从第一次调用函数到当前递归点的完整调用路径，因此，可以通过uptop接收递归点的返回值。

规则4有返回值的递归函数，需要在栈中保存每个递归点及递归函数本身的返回值，令re为递归函数的返回值，从上级返回后会保存在uptop.re中，则在递归点x处接收该返回值的方式为：top.rex = uptop.re。

2.3 Akman函数(多递归点)非递归化

算法9Akm函数递归程序(整理)

int Akm(int m, int n) {

int re, re1;

if(m == 0) re = n+1;

//递归停止条件

else if(n == 0) re = Akm(m-1, 1);

//语句1,递归点1

else {

re1 = Akm(m, n-1);

//语句2,递归点2

re = Akm(m-1, re1);

//语句3,递归点3

}

return re;

}

根据规则2，栈的设计如下：

(1) 发生变化的形参：m,n；

(2) 函数返回值：re，re1；

(3) 影响递归调用的局部变量：无。

算法10为根据规则3简化后的非递归程序。

算法10Akm非递归程序(简化)

int AkmS(int m, int n)

push(m, n);

while(!empty()) {

if(top.m == 0) {

//递归停止条件

top. re = top.n + 1;

pop();

}else if(top.state == 0) {

//进入函数

if(top.n == 0) {

//进入递归点1

top.state = 3;

push(top.m-1, 1);

} else {

//进入递归点2

top.state = 1;

push(top.m, top.n-1);

}

}else if(top.state == 1) {

//递归点2返回,进入递归点3

top.state = 2;

top.re1 = uptop.re;

//语句2

push(top.m-1, top.re1);

}else if(top.state==2||top.state==3) {

//递归点1, 3返回

top.re = uptop.re;

//语句1,3

pop();

}

}

return stack[0].re;

}

递归点1、3返回后执行的代码完全一致，它们的返回值作为递归函数的返回值，因此，可以将状态2、3合并。

2.4 N-后问题非递归化

算法11N-后问题递归程序

void nQueen(int r) {

if(r >= n) {

//递归停止条件

PrintMethod();

sum++;

}else {

for(int i = 0; i < n; i++) {

//for中：语句1(i=0; i

x[r] = i;

//语句2

if(Place(r)) nQueen (r+1); //语句3,递归点1

}

}

}

根据规则2，栈的设计为：

(1) 发生变化的形参：r；

(2) 函数返回值：无；

(3) 影响递归调用的局部变量：i(i的取值决定了递归调用的次数以及是否进入递归点)。

算法12为N-后问题的非递归程序。

算法12N-后问题非递归程序

void nQueenS(int r) {

push(r);

//i在push中被初始化为0

while(!empty()) {

if(top.r >= n) {

//递归停止条件

PrintMethod();

sum++;

pop();

}else if(top.state == 0) {

//进入函数

top.i = 0;

//语句1

if(top.i < n) top.state = 1;

//语句1

else pop();

}else if(top.state == 1) {

//进入递归点1

top.state = 2;

x[top.r] = top.i;

//语句2

if(Place(top.r)) push(top.r + 1);

//语句3

}else if(top.state == 2) {

//递归点1返回

top.i += 1;

//语句4

if(top.i < n) top.state = 1;

//语句4

else pop();

}

}

}

递归算法(算法11)for语句中的i

2.5 Perm函数(全排列)非递归化

算法13Perm函数递归程序

void Perm(int list[], int k, int m) {

if(k == m) printList(list, m);

//递归停止条件

else {

for(int i = k; i <= m; i++) {

//for中: 语句1(i=k; i<=m;)，语句4(i++; i<=m;)

swap(list[i], list[k]);

//语句2

Perm(list, k+1, m);

//递归点1

swap(list[i], list[k]);

//语句3

}

}

}

根据规则2，栈的设计为：

(1) 发生变化的形参：k；

(2) 函数返回值：无；

(3) 影响递归调用的局部变量：i。

算法14为Perm函数的非递归程序。

算法14Perm函数非递归程序

void PermS(int list[], int k, int m) {

push(k);

while(!empty()) {

if(top.k == m) {

//递归停止条件

printList(list, m);

pop();

}else if(top.state == 0) {

//进入函数

top.i = top.k;

//语句1

if(top.i <= m) top.state = 1;

//语句1

else pop();

}else if(top.state == 1) {

//进入递归点1

top.state = 2;

swap(list[top.i], list[top.k]);

//语句2

push(top.k + 1);

}else if(top.state == 2) {

//递归点1返回

swap(list[top.i], list[top.k]);

//语句3

top.i += 1;

//语句4

if(top.i <= m) top.state = 1;

//语句4

else pop();

}

}

}

2.6 二叉树后(先、中)序遍历非递归化

二叉树遍历的递归算法[12]比较简单。对于非递归程序，常见的基于“while-if”等框架的非递归算法中，先中序非递归算法采用的思路是：先沿左节点一直访问下去，直到左子树为空后再出栈访问一次右节点[9]。这种做法严格上不属于采用栈模拟方式的非递归化方法，因为栈中没有保存根结点到当前访问节点的完整路径(如只有右子树的情况)。而常见的后序遍历非递归算法在访问节点时先要区分是从“左枝”(递归点1)还是从“右枝”(递归点2)返回，因此入栈时需要将“访问标记”一同入栈。这样就使得栈中能够保存根结点到当前结点的完整路径，所以该类后序非递归算法属于栈模拟方式。一些二叉树的常见算法，如：求取任意两节点的共同祖先等，都需要利用后序非递归算法的框架完成，利用的就是其“栈中能够保存根结点到当前结点的完整路径”的性质。这个性质也是区分非递归算法是否属于栈模拟方式的重要特征。

利用本文提出的框架可以将二叉树遍历的非递归算法表达为更为简洁和通用的形式，见算法15。算法中，语句1放置在状态0、1、2处分别对应着二叉树的先、中、后序遍历。本文框架基于状态机思想，用栈严格地模拟了递归函数的调用过程，属于栈模拟方式，栈中保存了根结点到当前结点的完整路径。

算法15二叉树后序(先序、中序)遍历非递归算法

void tree_LRNs(BiTree T) {

push(T);

while(!empty()) {

if(top.T == NULL) pop();

//递归停止条件

else if(top.state == 0) {

//进入函数,进入递归点1

top.state = 1;

//语句1放此处为先序遍历

push(top.T -> lchild);

}else if(top.state == 1) {

//递归点1返回,进入递归点2

top.state = 2;

//语句1放此处为中序遍历

push(top.T -> rchild);

}else if(top.state == 2) {

//递归点2返回

printf(″%c ″, top.T -> data);

//语句1-后序遍历

pop();

}

}

}

3 结 语

利用状态机的思想，提出一种递归程序到非递归程序的转换框架。从转换实例可以看出，相比常见的“while-if”，“while-while”等非递归框架，本文提出的非递归框架思路清晰，代码简洁。只要将递归点的进入和返回行为进行状态编码，根据状态机模型和规则1-规则4，可以很快地将递归程序转换为非递归形式。同时本文框架具有程序化强的优点，进一步推广可以使计算机自动生成非递归程序代码成为可能。本文框架仅针对于直接递归的非递归化转换，对于较为复杂的间接递归的非递归化转换过程和规则，将作为进一步研究的重点。

[1] 汤亚玲.递归算法设计及其非递归化研究[J].计算机技术与发展,2009,19(11):85-93.

[2] 赵东跃.汉诺塔非递归算法研究[J].计算机应用与软件,2008,25(5):241-243.

[3] 陈瑞环,杨庆红,姚兴.使用递推解决递归问题的研究与应用[J].计算机应用与软件,2011,28(3):186-194.

[4] 谭罗生,吴福英,黄明和.Hanoi问题的解模型[J].计算机应用与软件,2004,21(10):49-51.

[5] Ivica M,Marin G.Comparison of heuristic algorithm for the N-Queen problem[C]//29th International Conference on Information Technology Interfaces,Cavtat,Croatia,IEEE,2007:759-764.

[6] Jun W,Hongfa W,Guoying Y,et al.Proving of the non-recursive algorithm for 4-peg hanoi tower[C]//International Conference on Electronic Computer Technology,Baoding,China,IEEE,2009:406-409.

[7] Liberios V,Zuzana B,Daniel M.Hanoi towers in resource oriented perspective[C]//15th International Symposium on Applied Machine Intelligence and Informatics,Herl′any,Slovakia,IEEE,2017:179-184.

[8] 孟林,李忠.递归算法的非递归化研究[J].计算机科学,2001,28(8):96-98.

[9] 李忠,尹德辉,孟林.递归算法非递归化的一般规律[J].四川大学学报(自然科学版),2003,26(2):209-212.

[10] 朱振元,朱承.递归算法的非递归化实现[J].小型微型计算机系统,2003,24(3):567-570.

[11] 杨春花,姚进,赵培英,等.一个递归算法非递归化的算法框架[J].计算机应用与软件,2010,27(9):81-84.

[12] 严蔚敏,吴伟民.数据结构(C语言版)[M].清华大学出版社,2016:128-131.