基于动态系统辨识的钢铁企业氧气管网系统的研究

张子阳 孙彦广

(中国钢研科技集团冶金自动化研究设计院 北京 100071)

0 引 言

氧气系统是钢铁企业重要的组成部分，高炉炼铁、转炉炼钢需要大量的氧气，同时氧气系统为连轧、连铸工艺过程提供氮气、氢气，氧气的消耗是钢铁企业技术气体消耗的重要部分，据统计，钢铁企业用氧量占氧气工业总产量的2/3[1]，大多数钢铁企业氧气放散率较高[2-3]，氧气系统对钢铁企业的进一步节能具有很大挖掘潜力。通过氧气管网建立模型和仿真模拟，为氧气系统的调度提供指导，对钢铁企业技术气体管网优化利用提供有力保障。

管网模型研究一直是国内外相关领域研究的重要问题[4-6]， 国内越来越重视对系统管网的研究，如今管网系统的研究大部分集中在天然气管网[7]、煤气管网[8]和蒸汽管网[9]，在钢铁氧气管网研究方面有如下研究：张培昆[10]基于混合整数线性规划方法建立管网调度模型，研究高炉开始休风期间管网初始压力对氧气放散率的影响；胡云芝等[11]运用BP人工神经网络算法建立数学模型，在MATLAB环境下开发了可反映各种不确定因素影响波动的情况下钢铁企业氧气用量的预测模型；倪健勇等[12]从控制氧气输送过程中的成本出发，通过对高压氧气管网实施降压措施，降低了高压氧气管网的输送压力，从而降低了氧气的输送成本；吴建福等[13]对转炉吹炼时的输氧管网动态特性进行了仿真模拟，分析了高压输气管网的压力波动与球罐群的位置和球罐数量有关。在以往的研究中，由于过于对假设过度的简化，造成管网系统精度不高。

目前国内外研究氧气管网运行优化方面主要集中在对特定目标函数的管网优化模型的求解，对于管网系统动态性能方面的研究较少。

随着管网建模研究的不断深入，如今模型已由线性推广到非线性，模型的约束条件更加具体，有效地提升了管网特征的精度，同时，模型应用的领域更多[14-15]。大部分对氧气管网建模研究属于理论建模，通过简化假设，建立描述氧气管网特性的方程，实现对管网系统的模型构建。但是管网系统通常是复杂的非线性系统，为了计算方便，增加模型的约束，导致模型精度不高，不能有效地描述管网系统的运行状态。

1 氧气管网动态运行特性模型辨识

氧气在管网流动特性建模可以用下面的方法：一种方法是通过机理分析建立系统的模型控制方程组，得到可接受的结果；另一种方法是在系统的输出为时间序列的基础上，再结合已知的输入建立模型[16-17]。本文通过系统输入、输出数据及管网的压力建立较为准确的系统模型，实现对管网系统的近似。由于氧气管网结构复杂，管网的流量随着压力不断变化，因此需要降低模型与实际运行工况的误差，采取对模型的主要影响因素进行辨识，使得该模型可以更加准确地描述管网的实际工况。

1.1 氧气管网动态模型的确定

系统辨识理论是系统的输入输出时间函数来确定描述系统行为的数学模型，尤为适用动态系统的描述。对于氧气管网系统，影响氧气在管网中流动的因素较多(如温度、压力、位置等因素)，综合这些约束来建立氧气管网模型较复杂。因此，应用系统辨识理论建立氧气管网的动态特性数学模型有一定的实际意义。

氧气管网的模型是在一定的数据基础上宏观建模思想，通过建立管网输入与管网累计流量之和作为输入，以监测点的压力为输出模型。与传统宏观模型不同，模型将用户使用氧气量作为未知变量，通过动态数据变化跟随氧气管网变化。

氧气管网系统可以表示为一个非线性动态系统，如果将用氧量作为不可测的扰动量，氧气管网可以表示为：

x(t)=f(x(t-1),u(t-1),d(t-1))

(1)

式中：x为管网状态变量，一般为管网压力，流量；u为控制变量，一般为制氧站压力和流量；d为用氧量。

通过研究氧气管网运行过程，选用ARX模型进行辨识。若所研究的氧气管网系统为MIMO系统，可以构建多输入多输出的ARX模型，模型可表为:

(2)

式中：ε(t)为干扰噪声(随机用户随机用氧量)。式(2)可理解为氧气管网下一时刻t的状态与上一时刻近似线性相关，并且与输入有着直接关系。

ARX模型是常用的辨识模型，根据管网系统的输入、输出信息建立数学模型，具有模型结构简单、鲁棒性强，是常用的非线性动态系统辨识模型。ARX模型可以表示为：

A(q-1)x(t)=q-ntB(q-1)u(t-1)+ε(t)A(q-1)=1+A1q-1+…+Anaq-naB(q-1)=B0+B1q-1+…+Bnbq-nb

(3)

式中：x(t)∈Rm×1是输出，u(t)∈Rp×1是输入，ε(t)∈Rr×1为白噪声(假设均值和方差均为零)，可表示为：

x(t)=[x1(t),x2(t),…,xr(t)]T

u(t)=[u1(t),u2(t),…,up(t)]T

ε(t)=[ε1(t),ε2(t),…,εr(t)]T

注:Aj∈Rr×r,j=1,2,…na,Bj∈Rr×p,j=1,2,…,nb，为待估计参数矩阵；q-1为后移算子，满足q-1u(t)=u(t-1)；na、nb为模型阶数，nk为系统时延。

1.2 模型的定阶与参数估计

对于氧气管网模型，首先用AIC定阶准则，来计算模型阶数和延时，具体步骤如下：

(1) 确定na、nb、nk的区间，确定不同阶数和延时的待辨识ARX模型。

(2) 模型参数的计算，通常采用估计得到相关参数，求得预测误差，并计算AIC指标：

IAIC≅ln(1+2nV/N)

式中：n是总数，N是采用的数据个数，V是模型预测误差平方和。

(3) ARX模型的确定是由AIC指标的决定的，为最小AIC指标的模型。

2 主管网系统的辨识

以某钢铁企业氧气管网系统为例，建立该钢铁企业氧气管网系统的ARX模型。从实际管网调控角度出发，通过监测的管网流量与压力来确定样本数据，采样时间为2015年5月21日至2015年5月24日，采样间隔为1分钟。

在处理氧气管网系统动态辨识的过程中，先确定系统的输入输出数据，即由进入管网的氧气量与用户消耗的氧气量之差的累积量(单位m3·h-1)为输入数据，由氧气管网的压力(单位MPa)作为输出数据。其中氧气流量差累积量u可以由流量计测得的输入输出流量获得，管网压力P可以由管网的压力计量装置获得。

系统模型结构如图1所示。

图1 系统模型结构图

根据氧气系统实际的采集数据，为了实现系统输入的充分性，所采用的数据变化范围较大，输入数据曲线如图2所示。

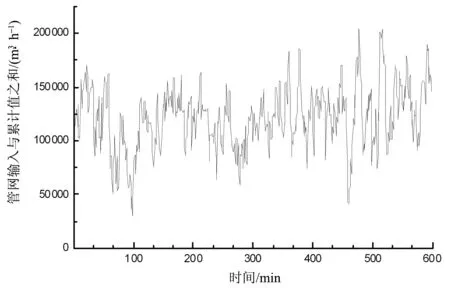
图2 输入数据曲线

输出数据如图3所示。

图3 输出数据

由输入输出曲线可知，此序列均值不为零的时变系统，把管网系统中的数据需要进行数据平稳化处理，对输入与输出时间序列进行处理可以去除部分趋势项。图4和图5为降噪后的重构信号。

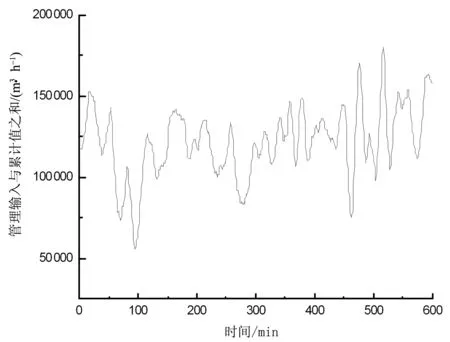
图4 降噪后输入数据

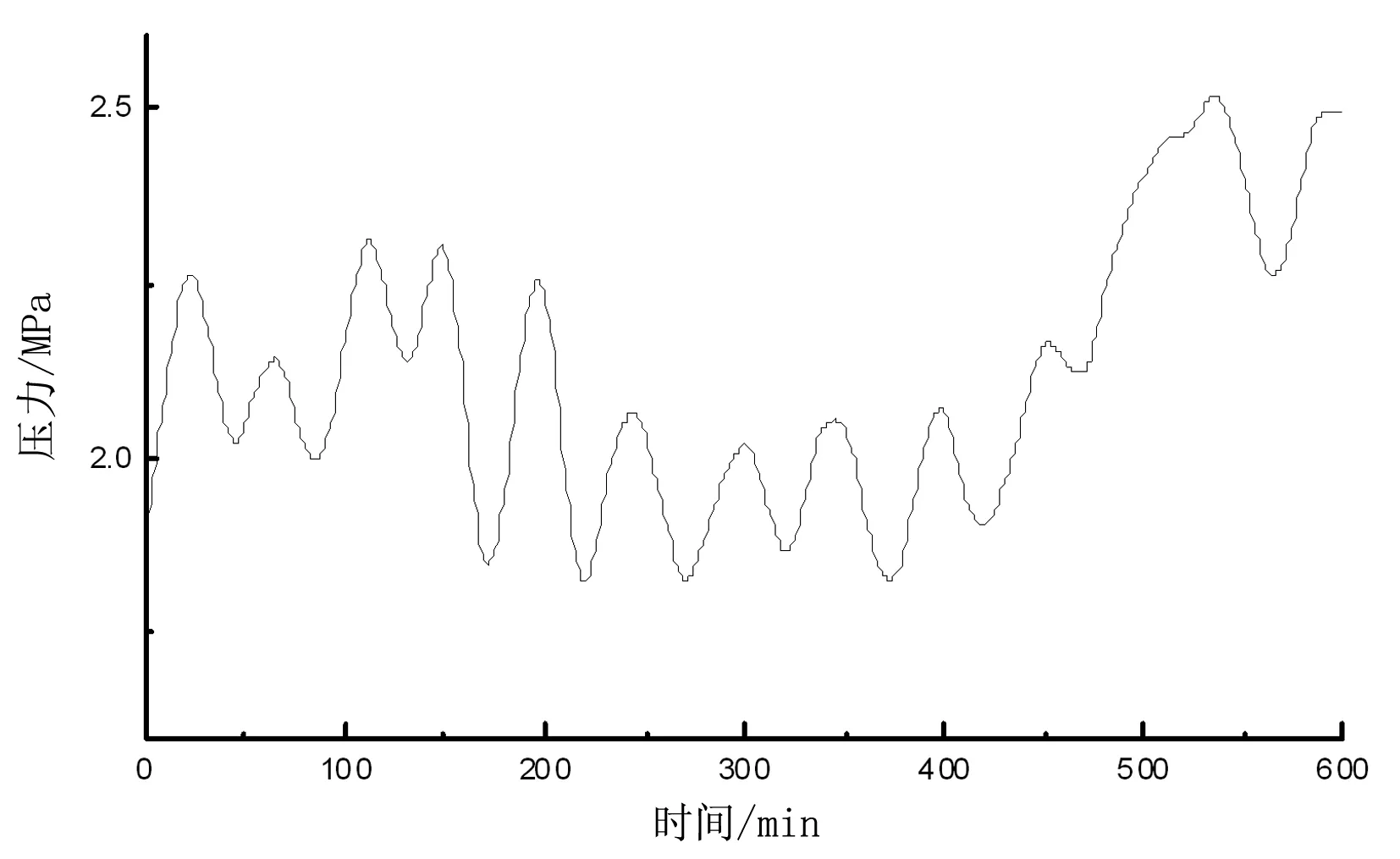
图5 输出数据输出数据曲线

根据前述辨识判据以及氧气管网实际运行时的输入输出数据，对候选模型的结构进行辨识，针对氧气管网系统中，氧气用户用氧量是随着时间不断变化，氧气管网系统状态随用氧量变化而变化。通过对氧气管网的ARX模型辨识，用氧量为时变扰动变量，采用基于递推最小二乘法对参数进行确定。引入具有鲁棒性和稳定性的实时辨识算法。

(4)

ε(t)=x(t)-θ(t-1)φT(t-1)

(5)

(6)

式中：P(t)为增益矩阵，H(t)为中间变量，F(t)为模型所需要的最小增益矩阵。ζ1(t)，ζ2(t)为遗忘因子。

通过采样提取了另一组数据(不同时段的采样数据)验证所得到的辨识模型的有效性如图6所示，并比较模型输出的结果与实测数据的误差如图7所示。

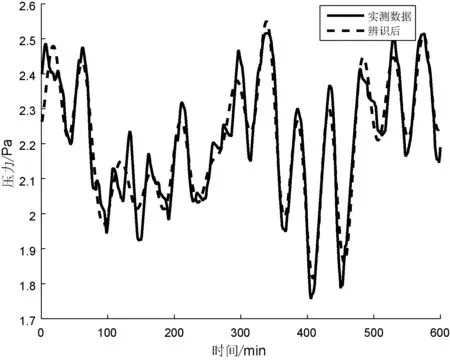
图6 模型输出与实际值

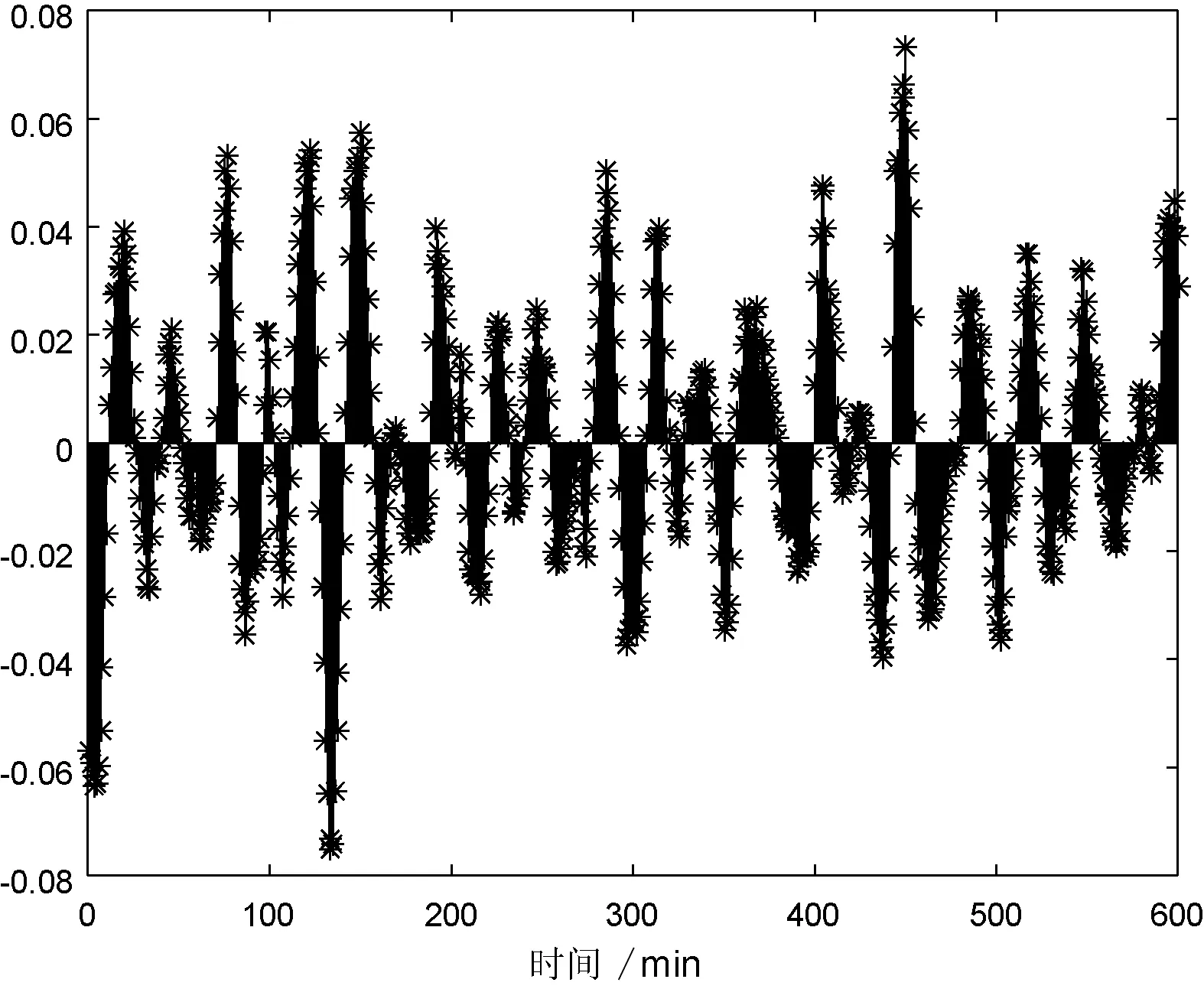
图7 误差分析

从图6所示管网输出压力的对比曲线可以看出，模型能够准确预测出管网系统运行不同状态的响应。从图7可以看出，氧气管网系统运动过程中，用户用量的不断变化以及故障检修等因素影响，得到的辨识模型输出与实测值之间的误差维持在稳定范围内。但是辨识的整体结果与实际数据基本保持一致，模型输出基本上能够拟合系统实际输出，验证了辨识模型的有效性。

3 不同用户管网系统的辨识

对不同用户模型数据与实际数据对比分析，进一步验证辨识所得模型的可靠性与适用性。钢铁企业的主要用户分为稳定用户和冲击用户，稳定用户对氧气用量恒定，冲击用户对氧气使用的不均衡度较大，冲击用户的波动极易造成氧气的放散，用户具体用氧量所占比例如表1、表2所示。

表1 稳定用户用氧百分比

表2 冲击用户用氧百分比

高炉和转炉同时运行时、多个转炉同时运行时进行验证，所得结果与实际运行的对比曲线如图8、图9所示。

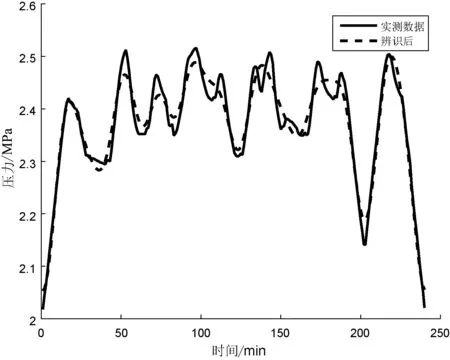
图8 高炉和转炉同时运行时对比曲线

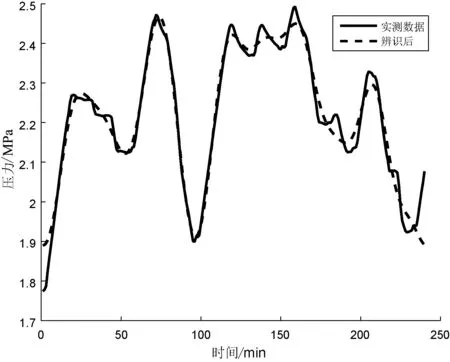
图9 多个转炉运同时行时对比曲线

从图8的对比曲线可以看出，高炉和转炉同时运行时，用氧量较大导致管网压力大部分时间较高。由于高炉氧气消耗较为平稳，为连续用氧用户，此时转炉用氧数量稳定，总体的氧气消耗量比较稳定，压力变化量不大。当多个转炉运同时行时，如图9所示，在100 min时由于炼钢用氧过度集中，供氧不足导致管网压力急剧下降。与常规理论模型的输出结果相比，本文辨识模型具有较好的跟踪性 ，辨识结果输出的压力更接近于实际系统的测量值，并且在不同用户辨识模型输出稳定。

4 结 语

本文结合钢铁企业氧气管网系统的运行特点和实际动态运行的影响，通过对氧气管网系统ARX建模，根据实测输入输出数据，首先选择系统模型阶次，然后用递推最小二乘法对模型参数进行确定，最后通过实测数据验证模型的有效性。在高炉和转炉同时运行时、多个转炉同时运行时不同工况进行验证，辨识所得到的模型能更准确地描述实际的系统运行状态。应用于氧气管网的运行仿真、预测和控制，可作为降低氧气放散率的重要手段。在对管网压力有要求的情况下，可以调节氧气管网辨识模型参数作为辅助手段进一步改善氧气管网调度效率。

[1] 蔡树梅.制氧系统电力消耗与经济运行[J].冶金动力,2015(8):26-28.

[2] 邵睿.降低氧气厂氧气放散率的研究[J].武钢技术,2015,53(5):23-27.

[3] 柳钢气体公司氧气放散率同比降低15.8%累计销售工业氧90000瓶[J].深冷技术,2016(1):21.

[4] Oliver M E.Economies of scale and scope in expansion of the US natural gas pipeline network[J].Energy Economics,2015,52:265-276.

[5] Chaudhary H,Kim Y,Kumar T,et al.Forecasting leaks in pipeline network:U.S.Patent 9,558,453[P].2017-1-31.

[6] 高鲁锋,郑海村.蒸汽管网水力热力耦合计算方法[J].中国科技论文,2013,8(8):812-815.

[7] Woldeyohannes A D,Majid M A A.Simulation model for natural gas transmission pipeline network system[J].Simulation Modelling Practice.and Theory,2011,19(1):196-212.

[8] 姜好.城市天然气管网供应可靠性模型分析[J].天然气技术与经济,2016,10(4):68-70.

[9] 马湧,孙彦广.贝叶斯神经网络在蒸气管网预测中的应用[J].中国冶金,2014,24(6):53-57.

[10] 张培昆,王立.高炉休风时供氧管网压力对氧气调度的影响[J].北京科技大学学报,2017,39(2):283-293.

[11] 胡云芝,张延平,胡帅.MATLAB神经网络模型预测钢铁企业氧气用量[C]//冶金循环经济发展论坛,2008.

[12] 倪健勇,何玉君,王忠润.降低氧气管网压力的实践[J].深冷技术,2011,33(3):1-3.

[13] 吴建福,童莉葛.高压氧气输送管网仿真分析[C]//中国金属学会.第七届(2009)中国钢铁年会大会论文集(中).北京:中国金属学会,2009.

[14] Nelles O.Nonlinear system identification:from classical approaches to neural networks and fuzzy models[M].Springer Science&Business Media,2013:36-45.

[15] Milanese M,Norton J,Piet-Lahanier H,et al.Bounding Approaches to System Identification[M].Springer US,1996.

[16] Reynders E,Wursten G,De Roeck G.Output-only structural health monitoring in changing environmental conditions by means of nonlinear system identification[J].Structural Health Monitoring,2014,13(1):82-93.

[17] Gkikas G D,Athanassoulis G A.Development of a novel nonlinear system identification scheme for the pressure fluctuation inside an oscillating water column-wave energy converter Part I:Theoretical background and harmonic excitation case[J].Ocean Engineering,2014,80(3):84-99.