半立方抛物线形断面收缩水深简化计算

沈 刚 ，彭 凯 ，王 洁 ，沈 洲 ，孙少江

（1．溧阳市水利局，江苏 溧阳 213300；2．扬州大学 水利与能源动力工程学院，江苏 扬州 225009；3．广东省水文局江门水文分局，广东 江门 529030）

明渠特征水深计算在水利工程设计中，由于抛物线类断面明渠的水力学特性较优，且断面稳定性好，在渠道工程中得到较为广泛的运用［1-2］。赵延风［3］和滕凯［4］等分别提出了一套可适用于各类抛物线形断面收缩水深的计算公式，赵延风的公式形式复杂，且需要通过迭代法提高计算精度，而滕凯的公式须查表确定参数，两者的计算过程均不够简便；代述兵等［5］提出的初值公式精度较低，运用迭代计算可提高精度，但增加了计算的复杂程度；陈诚等［6］将牛顿迭代法算法引入立方抛物线形断面收缩水深的计算，迭代计算收敛速度快但公式形式略显复杂不便于记忆；陈诚等［7-8］首次提出高次方程求解的迭代逼近—逐次优化拟合方法，并先后将其应用于立方和半立方抛物线形断面收缩水深的计算，其计算精度较高但公式略显复杂，本文借鉴该方法拟建立一套精度高且形式简捷的直接计算公式，便于工程设计人员直接应用。

1 无量纲收缩水深基本方程

半立方抛物线形断面曲线方程：

式中 a为半立方抛物线形断面的形状参数（m-1/2）。

收缩水深的基本方程为

式中 E0为以收缩断面底部为基准面的过水建筑物上游总水头（m）；hc为收缩断面处的水深（m）；Q为过水流量（m3/s）；g为重力加速度，通常取9.81（m/s2）；φ为流速系数，一般取0.80～1.00；Ac为收缩断面处的过水断面面积（m2）。

引入无量纲收缩水深x和无量纲参数k，即：

由式（1）～（4）可得半立方抛物线形断面无量纲收缩水深x的基本方程：

式（5）为x的高次方程，实际工程中可通过已知参数根据式（4）求得k值，但无法由式（5）直接解得x。

2 无量纲收缩水深简化计算公式

对式（5）进行简单的数学变换，得到迭代公式：

设迭代初值为x0，兼顾公式的精确性和简捷性，将其带入式（6）连续迭代3次，得：

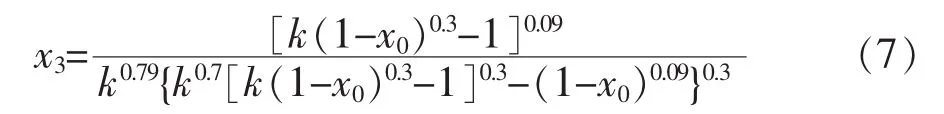
式中x∈［0.01，0.50］［3-4］，经过反复试算与分析比较，发现当迭代初值x0取0.25时，得：

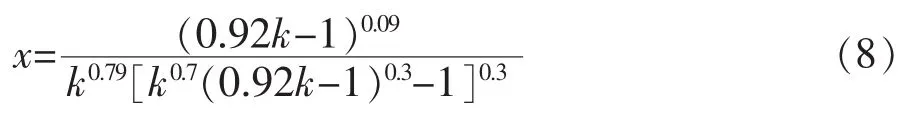
此时计算公式精度较高，且形式较为简捷。

3 误差分析与精度评价

3.1 误差分析

为验证式（8）的精确性，在［0.01，0.50］区间内以一定步长选取不同的x*，以此作为无量纲收缩水深的精确值，将其代入式（5）得k值，并将k作为已知参数代入式（8），可求得无量纲收缩水深的近似值x，及相对误差，可知hc与x的相对误差相同，计算结果如表1。

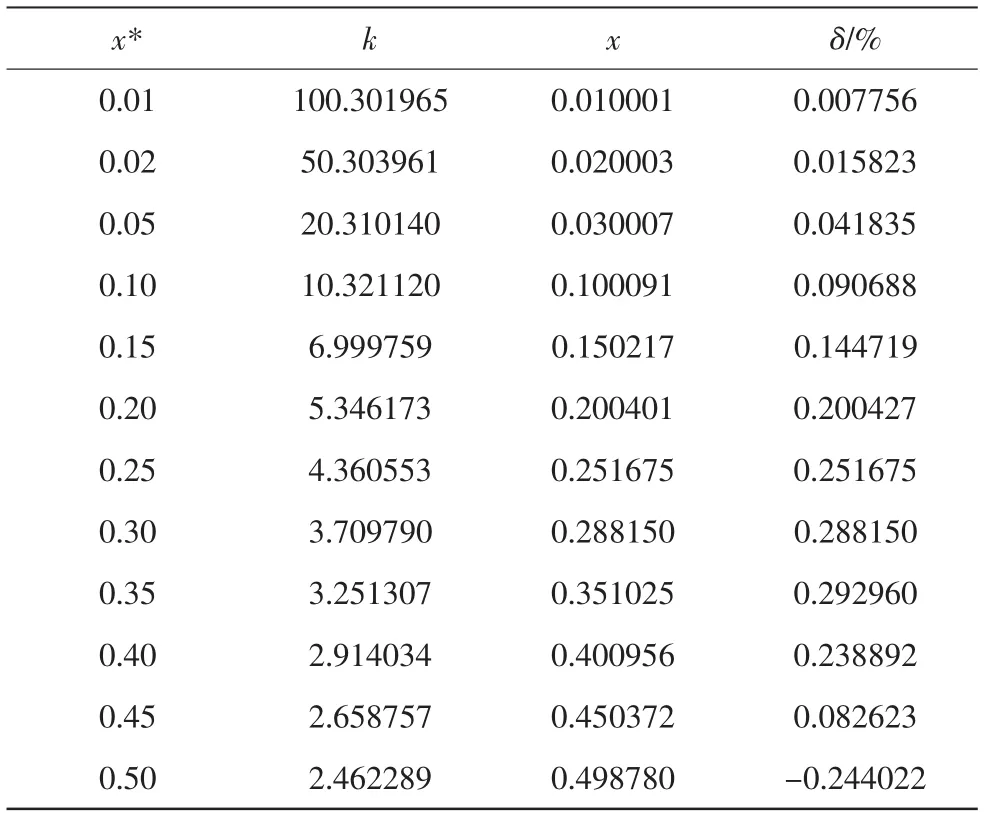
表1 新建公式相对误差

计算结果表明，在工程适用范围内，式（8）的相对误差呈先上升后下降的趋势，其最大相对误差绝对值仅为0.296%。 当x∈［0.01，0.4661］时，相对误差为正值，最大误差值为0.296%；当x∈（0.4661，0.50］时，相对误差为负值，最大误差值为-0.244%。

3.2 精度评价

表2为在x∈［0.01，0.50］工程适用范围内，由近年来提出的各种半立方抛物线形断面收缩水深直接计算方法求得的最大相对误差及评价。各式中n为断面方程幂函数的指数，对于半立方抛物线形断面n=3/2；B，γ分别为与n有关的系数。结果显示，当x∈［0.01，0.50］时，现有各类迭代初值计算公式最大相对误差绝对值从0.583%至5.439%不等，均须通过迭代计算提高精度，且公式形式较为复杂；而本文公式的最大相对误差绝对值仅0.296%，且形式简捷。所提出的直接计算公式不需要借助于迭代过程提高计算精度，通过较小计算量即可较精确地计算出半立方抛物线形断面的收缩水深，在工程实际计算中具有较为显著的优越性，可供工程设计人员参考使用。

4 应用举例

已知某闸前断面总水头E0=5m，通过渠道的流量Q=32m3，流速系数φ=0.95。若采用半立方抛物线形断面渠道，其断面曲线的方程为y=0.2|x|3/2，求闸后断面收缩水深hc的值（保留至10-3m）。

表2 现有计算公式的相对误差

4.1 参数k

将已知参数代入式（4），得k=5.0946。

4.2 收缩水深近似值x

将k值代入式（8）得，x=0.2112。

4.3 收缩水深hc

将x值代入式（3），计算收缩水深hc=1.056m。

通过试算法或计算机编程求得本算例收缩水深的精确值1.054m，故由本文公式算得收缩水深值的相对误差仅0.190%，精度完全满足工程实际应用要求。

5 结语

（1）借鉴高次方程近似求解的迭代逼近—逐次优化拟合方法，建立了一套新的半立方抛物线形断面收缩水深直接计算公式，形式简捷便于记忆。

（2）误差分析结果表明，在工程适用范围内该公式的相对误差介于-0.244%～0.296%之间，精度较高能够满足工程实际应用的需要。

参考文献：

［1］张伟，何武全．基于粒子群算法的抛物线形渠道断面优化方法［J］．灌溉排水学报，2017，36（4）：94-98．

［2］韩延成，徐征和，高学平，等．二分之五次方抛物线形明渠设计及提高水力特性效果［J］．农业工程学报，2017，33（4）：131-136．

［3］赵延风，王正中，刘计良．抛物线类渠道断面收缩水深的计算通式［J］．水力发电学报，2013，32（1）：126-131．

［4］滕凯．抛物线形断面渠道收缩水深简化计算通式［J］．水利水电科技进展，2014，34（3）：61-64．

［5］代述兵，刘韩生，卞晓卫，等．三种抛物线形断面收缩水深的直接计算公式［J］．长江科学院院报，2015，32（9）：90-93．

［6］陈诚，金城，赵程程，等．立方抛物线形断面收缩水深的牛顿迭代公式［J］．水科学与工程技术，2017（4）：1-2．

［7］陈诚，龚懿，王洁，等．立方抛物线形断面收缩水深的直接计算研究［J］．中国农村水利水电，2017（2）：173-175，181．

［8］陈诚，龚懿，沈刚，等．迭代逼近逐次优化拟合方法在水力计算中的应用研究［J］．水利水电技术，2017，48（6）：75-79．