非连续变形接触问题的分区有限元-块体界面元动力混合算法

李同春，樊舒婕，刘晓青，赵兰浩

（1.河海大学水利水电学院，江苏省南京市 210098；2.水资源高效利用与工程安全国家工程研究中心，江苏省南京市 210098）

0 引言

在水利工程中存在着许多局部不连续的现象，例如拱坝的横缝、岩体的裂隙、地基的软弱面等。这些局部不连续区域在地震等动力荷载作用下的张开、闭合和摩擦滑移关系着结构稳定与工程安全。考虑动载下不连续区域交界面的动态接触问题对于结构动力分析有着十分重要的意义。对于此类问题，已有的数值分析方法包括传统的有限元法FEM[1-3]、离散元法DEM[4，5]和非连续变形分析方法DDA[6-8]，以及FEM-BEM[9]、DEM-FEM[10-13]、DEM-BEM[14]等混合算法。

本文针对动力情况下非连续变形的接触非线性问题，基于文献[15]的力学模型提出了一种新的动力迭代求解方法。推导了包含接触力、块体形心刚体加速度和接触结点总位移在内的非线性方程，将该非线性方程与块体形心动力平衡方程进行耦合，建立了以界面接触力和块体形心刚体加速度为混合变量与界面结点总位移进行迭代求解的动力界面迭代方程，给出了混合解法的实施步骤并通过典型算例验证了动力混合解法的正确性。

1 IBE-PFE动力混合算法的力学表达

IBE-PFE动力混合算法将求解系统分解为若干块体与非连续界面，每个块体同时作为系统有限元的一个分区，以块体结点加速度作为分区有限元计算基本变量，以块体刚体形心加速度作为刚体运动变量，当接触界面上接触点对的接触内力增量已知，则可通过动力有限元法求出块体的加速度增量，进而根据Newmark法[16]求解各结点的应力和位移。建立接触界面上力与点对总位移方程，在块体形心处建立接触内力、块体形心加速度增量引起的力的平衡方程，将以上方程进行耦合，块体形心接触内力、加速度作为混合迭代变量和接触界面点对总位移的求解可以通过迭代方程求得。

2 IBE-PFE动力混合算法

2.1 动力分区有限元方程

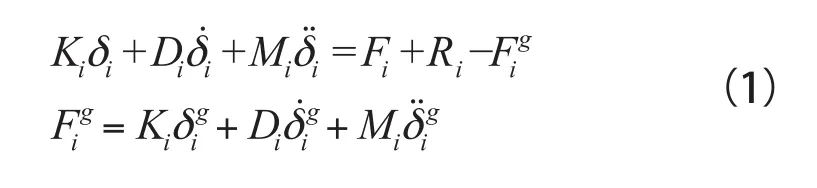
其中，Ki为刚度矩阵；Di为阻尼矩阵，这里采用瑞利比例阻尼假定Di=αMi+βKi，α、β为瑞利比例阻尼系数；Mi为质量矩阵，Fi为作用于第i个块体上的外荷载；Ri为由不连续界面上由内力传输的荷载向量，可由下式表示：

其中，Ti为该块体内结点上的作用力与接触点对上的接触力转换系数矩阵，FcL为局部坐标系下单元接触点对之间的接触力。

2.2 接触块体的刚性运动及动力平衡方程

如果第i块的形心位移被设为刚体位移变量，那么根据刚体运动法则，可视为块体内的每个点的刚体位移是与此相关、且遵守刚体运动法则的。在每一个接触块体形心点上分别建立块体力的平衡方程，对于每个块体，离散单元的动力平衡方程为：

其中，ωk为第k个结点相对于形心的转换矩阵。mi为与第i块块体的质量，Ii为与第i块块体相对于形心的转动惯量为质量阻尼系数，、为第i块块体的刚体加速度和刚体速度。npi为第i块块体的结点总数，Fk为作用在第k个结点的外荷载，Rk为作用在不连续界面上第k个接触点的接触内力。

2.3 时域方程离散化

在时域中，采用广义Newmark法[16]离散化有限元平衡方程（1）与动力平衡方程（3）。将离散后的（3）回带入方程式（3）可得时间步为n+1时块体形心的动力平衡方程如下，

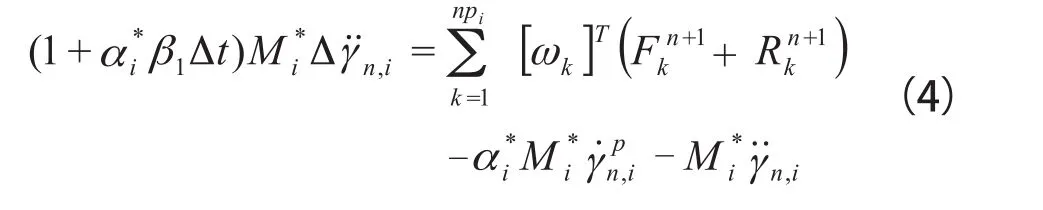
2.4 局部不连续边界的相对位移方程

局部不连续界面的相对位移方程可写作：

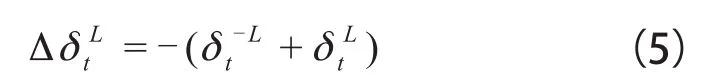
假设第i块块体中，不连续界面上接触点对的数目为nbi，对于每一个块体i，当时间步为n+1时各个点的整体位移为：

Ti为该块体内结点上的作用力与接触点对上的接触力转换系数矩阵，等式两边分别乘以整理可得：

其中，令

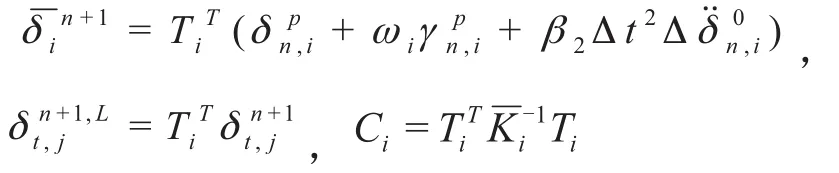
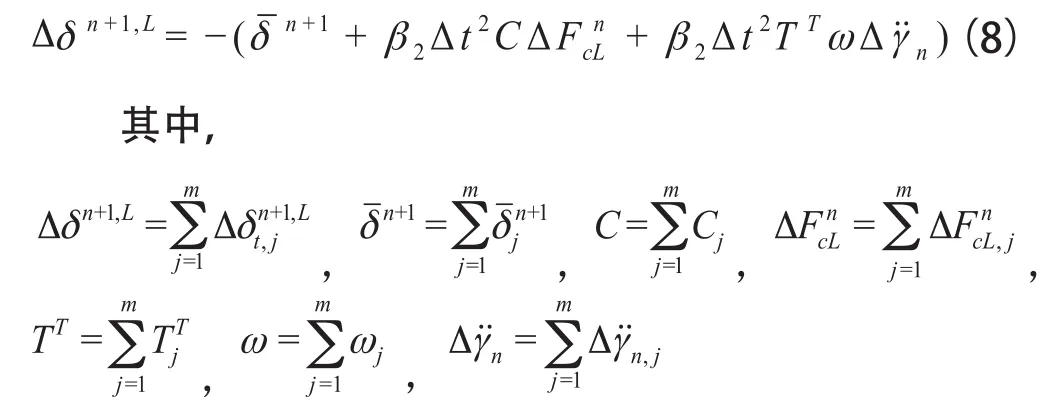
2.5 包含刚体转动位移和不连续边界接触力的混合求解方程

联立界面结点总位移方程和块体力的平衡方程可以得到的IBE-PFE混合算法的混合迭代方程。通过引入块体力的平衡方程后把接触力和块体形心刚体位移作为混合变量与结点总位移进行迭代，求解接触力增量与接触结点总位移增量之间的非线性关系得以实现。将式（1）、式（2）代入方程式（8）：

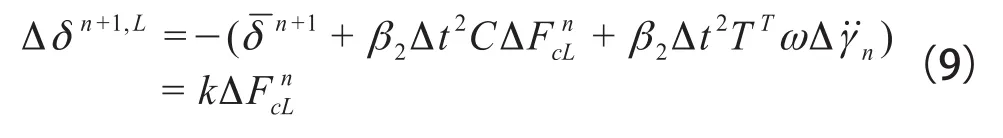
这里引入k来描述不连续界面之间的间隙状态，当k等于0时，Δδn+1，L为0，表示两接触体之间无位移差。式（9）进一步可改写为：

参考方程式（2），系统块体形心满足动力平衡方程，则对所有块体应用式（4），可得：

联立方程式（10）、式（11）可得：

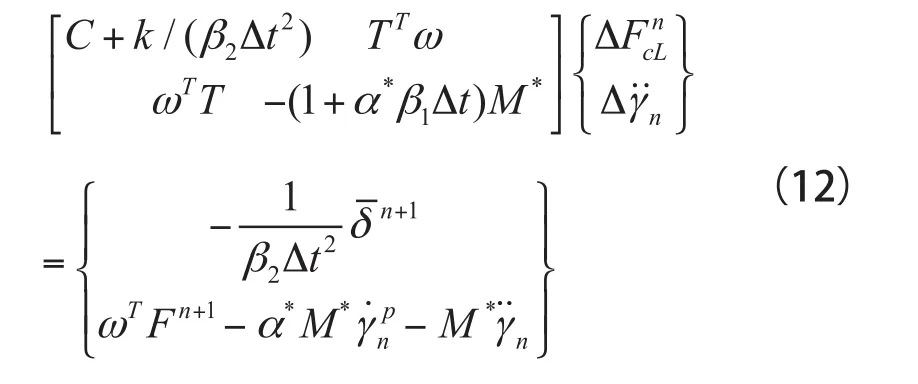
式（12）即为IBE-PFE动力混合解法的迭代方程。求解时将形心加速度增量视为混合迭代变量与界面结点动力总位移进行混合迭代求解。显然，该方法的迭代方程组具有对称性，可优化求解步骤，具有较高的求解效率。

3 算例验证

本算例以预设切口的混凝土三点弯曲梁受冲击荷载开裂为例，首先参考文献[17]建立有限元模型如图1所示，混凝土梁尺寸为228.6mm×76.2mm×25.4mm，2个支撑点之间的距离为203.2mm，预设裂纹长度为17.0mm，有限元模型共有414个单元、456个结点。在梁的中心点处施加冲击荷载，动力荷载施加方向垂直于梁，作用点位于跨中点，规定冲击荷载加载在试件中点处，因此混凝土梁受力状态为对称的，有限元模型可简化如图2所示，接触界面由14组接触点对模拟。混凝土梁的材料参数取值如表1所示，表中ρ为密度，E为弹性模量，v为泊松比，σρ为抗拉强度，ε为弹簧刚度。采用PFE-IBE方法计算该含缺口的混凝土简支梁受动力荷载作用下裂缝扩展的数值模拟解。

表1 混凝土材料参数Tab.1 Material parameters of the concrete specimen

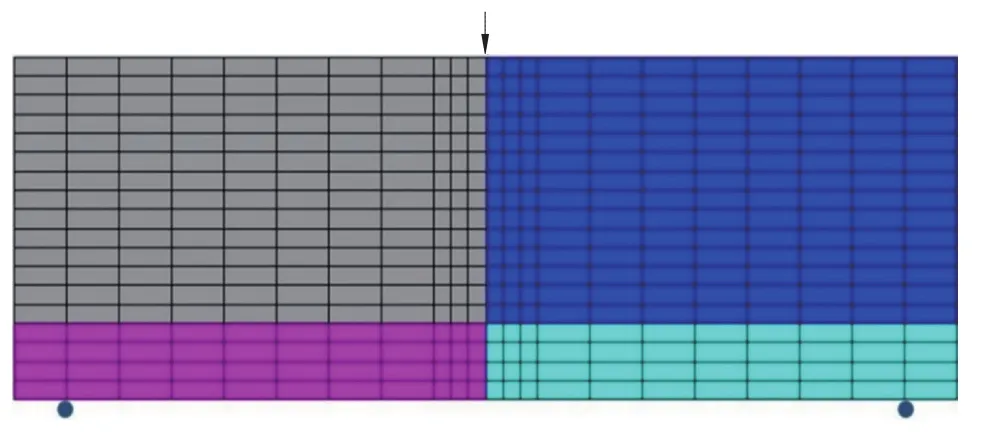
图1 预设切口的三点弯曲梁有限元模型Fig.1 Finite element model of a notched three-point bending beam

图2 梁左侧结构及接触点对示意图Fig.2 Configuration and finite element mesh of the left part

将IBE-PFE并与FEM结果[17]及Gopalaratnam和Shah试验[18]结果比较，图3中实验结果的测量存在着一定延时，但与数值计算结果对比延时极小；IBE-PFE开裂时程曲线的斜率与实验结果较为一致，说明模拟的开裂速率与实验较吻合。图4为同样计算条件下FEM与IBE-PFE的挠度时程曲线对比，结果吻合较好。

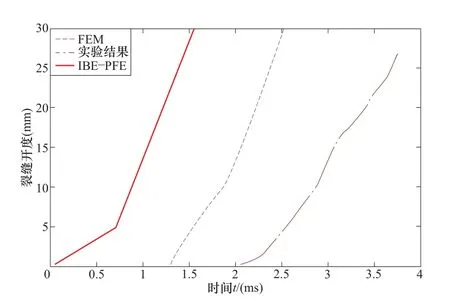
图3 混凝土梁开裂时程曲线Fig.3 Solutions of the crack extension history for the concrete beam

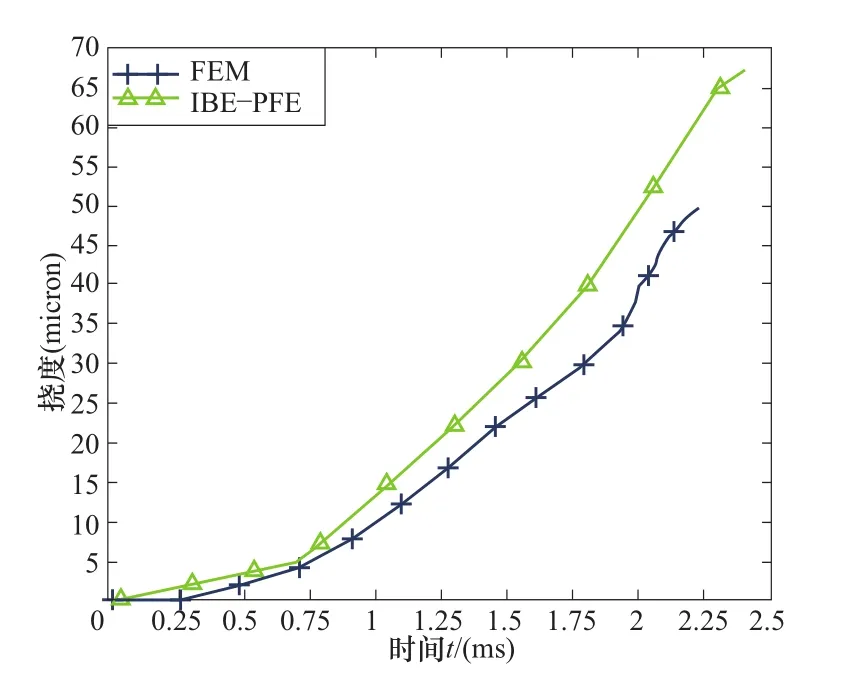
图4 混凝土梁挠度时程曲线Fig.4 Solutions of the deflection history for the concrete beam

4 结束语

本文基于IBE-PFE理论提出了一种新的动力迭代求解方法，并应用于求解局部非连续变形的动接触问题；详细阐述了IBE-PFE动力混合算法的力学表达和公式推导，实现了分区有限元与界面刚体元的结合，将求解系统分为若干块体和接触面，由接触状态形成界面柔度矩阵，非线性迭代仅在接触面上进行，提高了计算效率的同时保证了计算精度。数值算例的结果也证明了该方法的准确性和有效性。

[1] C.S.Desai，M.M.Zaman. Thin layer element for interfaces and joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics 1984，8（1）：19-43.

[2] A.Gens，I.Carol，E.E.Alonso. An interface element formulation for the analysis of soil-reinforcement interaction[J]. Computers and Geotechnics 1989，7：133-151.

[3] R.Buczkowski，M.Kleiber. Elasto-plastic statistical model of strongly anisotropic rough surfaces for finite element 3D-contact analysis[J]. Computer Methods in Applied Mechanics and Engineering 2006，195：5141-5161.

[4] B.C.Burman. A numerical approach to the mechanics of discontinue[D]. James Cook University of North Qeensland，Townsville，Australia，1971.

[5] P.A.Cundall，O.D.L. Strack A discrete numerical model for granular assemblies[J]. Geotechnique 1979，29（1）：47-65.

[6] G.H.Shi，R.E.Goodman. Two dimensional discontinuous deformation analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics，1985，9：541-556.

[7] L.Jing，Y.Ma，Z.Fang. Modeling of fluid flow and solid deformation for fractured rocks with discontinuous deformation analysis（DDA）method[J]. International Journal of Rock Mechanics and Mining Sciences，2001，38：343-355.

[8] J.Liu，X.J.Kong，G.Lin. Formulations of the three-dimensional discontinuous deformation analysis method[J]，Acta Mechanica Sinica，2004，20（3）：270-282.

[9] Humberto Breves Coda. Dynamic and static non-linear analysis of reinforced media ：a BEM/FEM coupling approach[J].Computers and Structures，2001，79 ：2751-2765.

[10] J.L.Xu，Z.P.Tang. Combined Discrete Finite Element Multiscale Numerical Method and Its Application[J]. Chinese Journal of Computation Physics，2003，6 ：477-482.

[11] N.Guo，J.D.Zhao. A coupled FEM/DEM approach for hierarchical multiscale modelling of granular media[J]. International Journal for Numerical Methods in Engineering，2014，99（11）：789-818.

[12] Mark Michael，Frank Vogel，Bernhard Peters. DEM–FEM coupling simulations of the interactions between a tire tread and granular terrain[J]. Computer Methods in Applied Mechanics and Engineering，2015，289：227-248.

[13] X.Q. Liu，T.C. Li，L.H. Zhao. An Iteration Algorithm based on Mixed FEM and DEM for Safety Factor of Slope Stability with Determined Sliding Surface[J]. Applied Mathematics and Athematics and Information Sciences，2012，6（3）：721-725.

[14] S.G Chen，J. Zhao. Modeling of Tunnel Excavation Using a Hybrid DEM/BEM Method[J]. Computer-Aided Civil and Infrastructure Engineering，2002，17（5）：381-386.

[15] T.C. Li，X.Q. Liu，L.H. Zhao. An interactive method of interface boundary elements and partitioned finite elements for local continuous discontinuous deformation problems[J].International Journal for Numerical Methods in Engineering，2014，100（7）：534-554.

[16] WANG Xiaojian，LI Tongchun，HE Jinwen，et al. Application of IBE-PFE method to analysis on stability of slope around flood discharge tunnel outlet of a hydropower station [J].Water Resources and Hydropower Engineering，2017，48（3）：140-145，157.

[17] M.G.Katona，Zienkiewicz. A unified set of single-step algorithms，Part3：the beta-m method，a generalization of the Newmark scheme[J]. International Journal for Numerical Methods in Engineering，1985，21：1345-1359.

[18] Jiaji Du，Albert S. Kobayashi，Neil M. Hawkins.FEM Dynamic Fracture Analysis OF Concrete Beams[J].Journal of Engineering Mechanics，1989，115（10）：2136-2149.