基于抽象素养视角下的代数思维培养研究

莘义成

在人教版初中数学《2.1整式（1）》教学中，基于丰富的现实情景和学生已有基础设计合理的抽象活动，让学生经历用字母表示数抽象的主要活动，在活动中积累数学抽象活动经验，发展符号意识和数学抽象素养。下面以《2.1整式（1）》为例谈谈如何帮助学生实现从数到代数的过渡，发展代数思维。

教学片断

一、创设情景，提出问题

问题1：青藏铁路线上，在格尔木到拉萨之间有一段很长的冻土地段。列车在冻土地段的行驶速度是100 km/h，列车在冻土地段行驶时，根据已知数据求出列车行驶的路程。

（1）2 h行驶多少千米？3 h呢？… t h呢？你能提出哪些数学问题？

师生活动：学生独立回答问题，提出了“字母可以表示什么数？”“怎么样用字母表示数？”“为什么要学习用字母表示数”等问题。

评析：通过设问，引发学生发现问题和提出问题，学生从“是什么、为什么、怎么做”的角度提出了自己想研究的问题，激发学生的问题意识和求知欲。

（2）字母t表示时间有什么意义？如果用v表示速度，列车t h行驶的路程是多少？

（3）回顾以前所学的知识，你还能举出用字母表示数或数量关系的例子吗？

师生活动：学生独立回答后在教师引导下归纳，用字母t可以表示时间，字母t可以像数一样参与运算。此外字母表示的范围广泛，如数学公式、法则、性质、运算律等，及总结用字母表示数需要注意的问题。

设计意图：让学生经历由数到式的过程，感受从特殊（具体）到一般（抽象）的认识过程，体会用字母表示数的简洁性和必要性。学生通过范例感受字母可以表示数，字母可以参与运算，为下面继续学习用含有字母的式子表示数量关系做到方法上的引导。

二、探究关系，解决问题

问题2：怎样分析数量关系，并用含有字母的式子表示数量关系呢？

例1：（1）苹果原价是每千克p元，按8折优惠出售，用式子表示现价；

（2）某产品前年的产量是n件，去年的产量是前年产量的m倍，用式子表示去年的产量；

（3）一个长方体包装盒的长和宽都是a cm，高是hcm，用式子表示它的体积；

（4）用式子表示数n的相反数。

师生活动：学生先思考，然后和同桌交流，学生代表演板、展示，师生共评。

追问：（1）苹果现价比原价降低了多少？你能再赋予0.8p一个含义吗？

（2）前年与去年产量的和是多少？去年的产量比前年多多少？你能再赋予mn一个含义吗？

（3）这里数n一定是正数吗？

评析：熟悉用含有字母的式子表示实际问题中的数量关系，并体会一个含有字母的式子可以表示多种不同的含义，理解字母可以像数一样参与运算，为形成单项式的概念做铺垫，在用数学符号表示数量关系中，感受其中“抽象”的数学思想。

例2（1）一条河的水流速度是2.5km/h，船在静水中的速度是vkm/h，用式子表示船在这条河中顺水行驶和逆水行驶时的速度；

（2）买一个篮球需要x元，买一个排球需要y元，买一个足球需要z元，用式子表示买3个篮球、5个排球、2个足球共需要的钱数；

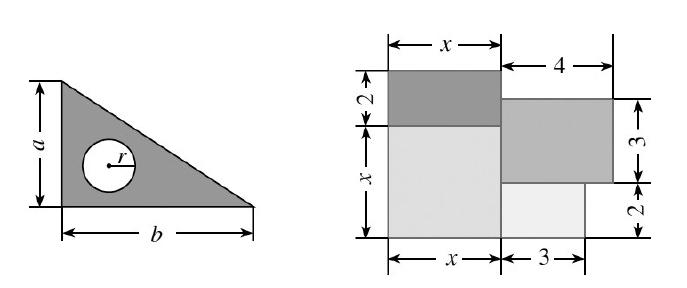
（3）如左下图（图中长度单位：cm），用式子表示三角尺的面积；

（4）右上图是一所住宅的建筑平面图（图中长度单位：m），用式子表示这所住宅的建筑面积。

师生活动：学生先独立思考、列式，然后同桌交流，教师组织学生全班展示，师生共同归纳，列式就是把实际问题中与数量有关的语句，用含数、字母和运算符号的式子表示出来，也就是把文字语言转化为符号语言。分析问题时应抓住关键词语，明确它们的意义及关系；理清语句层次，明确运算顺序；联想相关概念和公式，字母可以和数一样进行运算。

追问：（1）如果船在河中顺水行驶，3 h行驶多少千米？

（2）当x=70，y=50，z=80时，式子3x+5y+2z的值是多少？你能再赋予3x+5y+2z一个含义吗？

（3）列式书写应该注意什么？

师生活动：问题（1）（2）学生独立代入计算；赋予3x+5y+2z一个含义，鼓励学生发散思维，从不同的角度去解释；第三问由师生共同归纳注意事项。

评析：进一步熟悉用含有字母的式子表示实际问题中的数量关系，体会字母的丰富含义。经历由“特殊→一般→特殊”的过程。进一步理解字母可以像数一样进行运算，为形成多项式的概念进行铺垫，在用数学符号表示数量关系中，感受其中“抽象”的数学思想。

例3 （1）观察下列各式：x，2x2，3x3，4x4，……按此规律，第n个式子是 。

师生活动：学生通过观察、分析，归纳发现规律，并用含字母的式子表示一般結论。

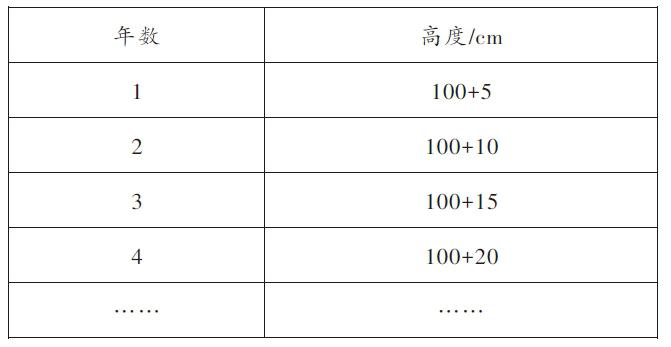
（2）测得一种树苗的高度与树苗生长的年数的有关数据如下表（树苗原高100 cm）：

前四年的变化和年数有什么关系？假设以后各年树苗高度的变化与年数保持上述关系，用式子表示生长了n年的树苗高度。

师生活动：教师引导学生归纳，用整式表示实际问题中的数量关系和变化规律，可以从特殊值入手，借助表格分析，由特殊到一般，由个体到整体地观察、分析问题、发现规律，并用含字母的式子表示一般的结论，这体现了由特殊（具体）到一般（抽象）的认知规律。

评析：借助具体的式子或表格，通过观察、分析、归纳发现规律，并用式子表示数量关系和变化规律，经历由特殊到一般的过程，使学生进一步感受从特殊到一般的认知规律，体会到用字母探索和表达一些规律的便捷，认识到字母比数字更具有一般性。

问题3：上面的问题中，既有已知数，又有字母表示数，字母表示数有什么意义？用含有字母的式子表示数量关系有什么意义？

师生活动：用字母表示数，字母和数一样可以参与运算，可以用式子把数量关系简明地表示出来。

评析：进一步理解字母表示数的意义，理解用含有字母的数学式子表示实际问题中数量关系的简洁性、必要性和一般性。

三、介绍由数到代数的历史，感悟数学文化

我们探讨了用字母表示数，你有什么体会？你知道在人类历史上，是如何发明用字母表示数呢？教师用多媒体介绍由数到代数的历史。

评析：利用多媒体介绍由数到代数的发展史，让学生在数学史中汲取养分，激发学生学习兴趣，感受数学文化的魅力，提高数学素养。深入理解字母表示数的过程，不是简单地用字母代替数的过程，而是具体数量符号化、从特殊到一般的抽象化过程。

总评

用字母表示数，看似简单，实则不然。它肩负着帮助学生从算术思维向代数思维进行过渡的任务，是学习和认识数学的一次飞跃，同时也是学生今后继续学习代数式、整式、分式和根式等概念及相关运算的重要基础，具有非常重要的意义。

课堂上学生经历从“具体事物——分析数量关系——学会数学地表示”这一逐步符号化、一般化的过程。学生通过观察、分析和归纳得出一般规律，获得对代数对象及其运算的知识。体现了学生以经历发现问题、提出问题、分析问题、解决问题的过程，教师进行代数思维培养的核心任务便完成。

1.借助丰富情境，加深对字母表示数的理解

从字母表示的“数”的对象来看，字母是数的化身，但从本质上看字母又不同于数。教学中，给学生提供生活中常见的情景和具体事例，让他们在熟悉的环境中反复体会字母表示数的现实性。先让学生用算式表示问题的结果，再通过改变具体数量，抽象地用字母表示数，写出相应的含有字母的式子。又如例3的两个问题，用字母表示数量关系和变化规律，得到具有一般性的结论。有助于学生理解字母的使用是数学表达和数学思考的重要形式，初步感受学习过程中数式通性的原理。

2.经历数学抽象过程，发展数学抽象素养

学生完整地经历用字母表示数这一研究对象的发现、提出。通过创设情境，例1，例2，例3中的问题，在分析数量关系的同时，用自己的语言进行描述，并在师生互动过程中运用字母将这个关系和规律表示出来。自然合理地完成从数到字母表示数的抽象过程，即把日常语言抽象成数学语言（数量关系式），进而转换成符号语言。学生通过多次经历这些用字母表示数学抽象的活动，可以积累数学抽象的活动经验，发展数学抽象素养。

3.体验数学思想，增强学生对代数思维内涵的理解

“用字母表示数”能够简洁地表示实际问题中的数量关系，方便地表达一般规律，是对数量关系的概括性表述；在“求含有字母的式子的值”的学习中，通过将每一个变量取定一个数值代入式子，经运算而获得一个确定值的过程，使学生体会“对应”的思想，领悟“变化”与“确定”之间的辩证关系。将内容所蕴含的特殊与一般、运动与变化的数学思想方法及教育价值，不露痕迹地渗透于教学过程中，体会字母比数更具有一般性，揭示数与式的联系和区别——数可以看成是式的特殊情况，数的运算可以看成是式的运算的特殊情形，促进学生对所学知识的理解与掌握，提高认识能力，形成良好的数学素养。

4.感悟数学文化，体会从数到代数的进步

用字母表示数是人类知识由具体到抽象的一次飞跃，是人类千百年来思维抽象的结晶。教学中，学生在学习知识的同时，体会由数到代数的过渡中所蕴含的丰富数学文化，从而全面地感悟人类对认识客观世界中数量关系的不断探索，了解人类从数到用字母表示数这个重要的进步。教学中通过用字母表示运算定律、公式、数量关系、变化规律，使学生感受到数学的符号语言比文字语言更简洁明了，积累这样的体验和认识，对于提高学生的学习兴趣和理解能力都有很大的帮助。这样才能使数学课更具有活力，达到德育、智育的雙重教育目的。

5.夯实基础，代数思维的培养是一个循序渐进的过程

本节课具有承前启后的作用，是在小学已学过简单的字母表示数的基础上，进一步地抽象探究。本节课重点回答了“为什么要用字母表示数”“字母可以表示哪些数”“如何用字母表示数”及用字母表示数时书写规范、注意事项等。它是学习代数的重要基础，是由算术思维向代数思维过渡的关键环节，切不可轻描淡写，而要浓墨重彩。对绝大多数学生而言，经历认识上的这个过渡时期，都需要反复体验。教师应分层次地安排抽象活动，实现语言概括到字母表示的对比、过渡和加深，激发学生进一步体验符号语言的兴趣。与此同时，教师还应着眼于学生的发展，整体把握教学目标，不断地为学生完成认识上的飞跃打好基础。

（作者单位：枣阳市钱岗中学）