基于BP神经网络对非线性函数拟合

广东理工学院电气工程系 吴 琼

以生物学基础的BP网络为全局网络，于多变量函数逼近理论不同，BP神经网络是输入输出的映射，其优势在诸多方面比函数逼近理论要更为明显。本质上，神经网络是一个非线性系统，任意复杂的非线性函数它都能够充分逼近。良好的鲁棒性、联想记忆能力、容错性高及并行处理信息等优异特性使神经网络成为智能领域中的重要算法之一[1-2]。

1.BP神经网络的结构与原理

图1 多层神经网络结构

图1所示为多层神经网络结构。其中，n表示输入层神经元个数，l 表示隐含层中神经元个数，m为输出层神经元个数。ωij、ωjk为连接权值，分别表示输入层第 i 个神经元和隐含层第 j 个神经元、隐含层第 j 个神经元与输出层第k个神经元之间的权值。取线性函数作为输入层神经元的作用函数，即神经元的输入和输出相同。分别将隐含层和输出层神经元的上一层神经输出加权和对应作为他们的输入，激励程度和作用函数决定了各个神经元的输出[3]。

基本BP算法包括两个方面：信息的前向传播和误差的反向传播。计算实际输出时，按从输入到输出的方向进行；而权值和阈值的修正从输出到输入的方向进行。

(1)信息前向传播过程[4]

对于图1，设各神经元的阈值为0，便于后续分析。

(2)误差的反向传播过程

误差的方向传播，即首先由输出层开始逐层计算各层神经元的输出误差，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络的最终输出能接近期望值。

2.仿真实验

利用BP网络拟合非线性函数：

给出不同隐含层的BP网络拟合结果比较图，最大训练步数1000步，目标函数误差。

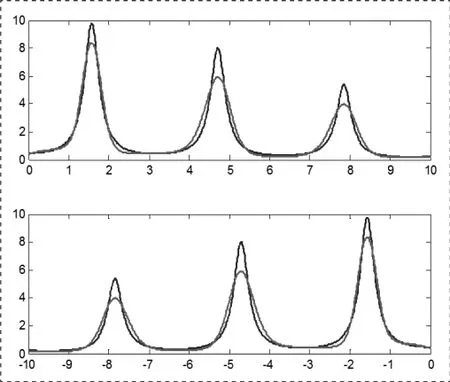
图2 10个隐含层节点的BP网络拟合效果虚线是BP网络输出

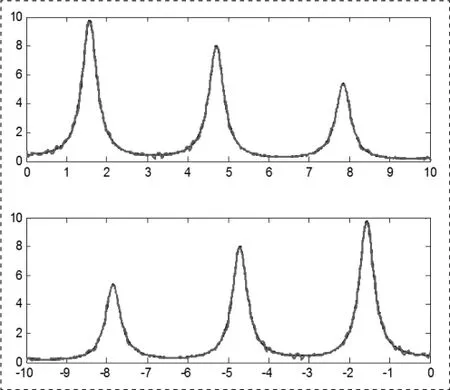
图3 100个隐含层节点的BP网络拟合效果虚线是BP网络输出

从仿真图可看出利用BP网络拟合非线性函数具有良好效果。

3.结束语

本文简单介绍BP神经网络的原理和特点，在此基础上对非线性函数进行拟合。仿真结果表明，利用BP神经网络能将拟合误差控制在很小的范围之内，印证了其拟合的有效性。

[1]周妮娜．基于BP神经网络的非线性系统辨识[J]．新技术新工艺,2008(10)∶36-37．

[2]吴琼,任瑾．基于数据滤波的极大似然递推最小二乘辨识[J]．电子世界,2017．

[3]程森林,师超超．BP神经网络模型预测控制算法的仿真研究[J]．计算机系统应用,2011(8)∶100-103．

[4]张宝堃,张宝一．基于BP神经网络的非线性函数拟合[J]．电脑知识与技术,2012,8(27)∶6579-6583．