60°坐标系下三电平逆变器SVPWM算法研究

童 军，张 倩，路 尧，王侠辉

(西安科技大学，西安 710054)

0 引 言

近年来，由于多电平逆变器在高电压、大功率场合应用的越来越多，人们对其越来越重视，因此提出了多种拓扑结构的主电路，对其进行了深入的研究和探讨。多电平逆变器即是利用多电平阶梯波来无限逼近正弦波，同时它的产生可以克服两电平逆变器较高的电压变化率dudt和较高的电流变化率didt等缺点[1-2]，而研究多电平逆变器要以三电平逆变器理论为基础。SVPWM技术是将计算机与PWM技术完美结合。通过控制空间电压矢量，以实现磁链轨迹无限逼近圆形为目的。它具有很小的谐波影响，且兼具较高直流利用率的优势，因此受到人们越来越多关注，在变频调速技术中大放异彩，得到了广泛应用[3]。

本文采用的60°坐标下SVPWM控制算法，由于采用非正交的60°坐标系，使得在确定参考电压矢量的位置和计算基本矢量的作用时间时，相较于传统的SVPWM控制算法会更简单，避免了繁琐的三角函数计算，大大减少了计算的工作量。

1 二极管箝位型三电平逆变器原理分析

图1二极管箝位型三电平逆变器主电路拓扑图

逆变器处于工作状态时每一个桥臂每次有且仅有两个开关管导通，VT11和VT13互补导通，VT12和VT14互补导通，其中VT11和VT12导通时输出电压为Ud/2，中间两个开关管导通时输出电压为0，VT13和VT14导通时输出电压为-Ud/ 2，即输出有3种状态1(P)，0(O)，-1(N)，三相组合共有27种开关状态。

若定义Sa，Sb，Sc为a，b，c三相的开关输出状态，则三相输出电压可表示：

将三相静止坐标系转换为α-β坐标系，转换方法：令α坐标轴与A相坐标轴重合，α轴逆时针旋转90°得到β轴，将期望合成参考电压矢量分解到α，β轴上，就可得到两坐标系下的转换关系：

则合成参考电压矢量：

式中：j为复系数；ρ为旋转因子；ρ=ej2π/3。

由式(3)可得，输出基本矢量按照其模长大小可分为零矢量、小矢量、中矢量和长矢量，各个矢量的模长分别为0，Ud3,3Ud3,2Ud3。图2为三电平SVPWM电压矢量的空间分布。

依据我国康复治疗技术岗位任务分析的研究[6]，对言语治疗技术岗位工作任务的分析共列举了6项，结果显示，ST岗位需要掌握的前四项任务分别是ST4、ST6、ST2、ST5，提示在言语治疗中对失语症康复需求较多，此外，吞咽功能的康复也是言语康复的重点任务（见表5）。

图2三电平SVPWM电压矢量的空间分布

2 直角坐标系下的SVPWM算法

传统SVPWM算法是将三电平的输出空间电压矢量按60°每分隔为一个扇区，总共6个扇区，用Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ表示；再将每个扇区又分别划分为4个小区域，如图3所示，用1，2，3，4表示小区域。

图3传统算法下第一扇区小区域的划分

由于扇区是以60°划分的，因此对于扇区的判断，可以通过参考电压矢量的角度来判定。若用[X]表示对X进行取整，θ表示参考电压矢量Uref的角度，θ∈[0°,360°]。则当[θ/60°]=1时，参考电压矢量在第一扇区；当[θ/60°]=2，参考电压矢量在第二扇区，以此类推，依此就可确定参考电压矢量的位置。

如图3所示，以第一扇区为例，将第一扇区分为4个小部分，以第3部分的边界线为3个判据。利用3个顶点的坐标，则小区域的判断方法[5]：

(4) 若Uref不满足以上任一条件，则参考矢量在小区域3。

以第一扇区第3部分为例，确定参考矢量所处的区域后，根据临近三矢量合成原则，利用临近的3个基本矢量u1，u2，u3合成参考矢量Uref，根据空间电压矢量合成的伏秒平衡原则，有：

u1T1+u2T2+u3T3=UrefTs

(4)

T1+T2+T3=Ts

(5)

表1直角坐标系下第一扇区各矢量作用时间

区域T1T2T312kTssin(π3-θ)2kTssinθTs[1-2ksin(π3+θ)]2Ts[1-ksin(π3+θ)]Ts[2ksin(π3-θ)-1]2kTssinθ3Ts(1-2ksinθ)Ts[1-2ksin(π3-θ)]Ts[2ksin(π3+θ)-1]4Ts(2ksinθ-1)2Ts[1-ksin(π3+θ)]2kTssin(π3-θ)]

同理可求出当参考电压位于其他扇区小区域时每个基本矢量的作用时间。

3 60°坐标系下的SVPWM算法

由上一节可以看出,传统直角坐标系下SVPWM的算法中，判断空间电压矢量所在位置和确定矢量作用时间时存在大量的三角函数的计算，大大增加了计算工作量，因此引入基于60°坐标系下的SVPWM算法。

由于对于扇区的划分是以60°为一扇区的，因此可以采用非正交的60°为坐标系实现SVPWM算法。

重新建立坐标系，令α轴为g轴，g轴逆时针旋转60°为h轴，得到g-h坐标系。设此时参考矢量Uref的坐标为(Ug,Uh)，则可得到60°坐标系下的电压表达式：

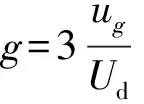
图460°坐标系下电压矢量空间分布图

对于大扇区的判断方法与传统直角坐标系下的方法相同，以参考矢量的角度为基准，计算其所在扇区。

同样以第一扇区为例，确定参考矢量的具体位置。与直角坐标系相比，60°坐标系下将参考电压矢量Uref简化为(g，h)的坐标为整数，同样用第2小区域的3条边界线作为判据更为简单直接。则小区域的判断方法如下：

(1) 若Uref满足g+h<1,则参考电压矢量落在小区域1；

(2) 若Uref满足g>1,则参考电压矢量落在小区域3；

(3) 若Uref满足h>1,则参考电压矢量落在小区域4；

(4) 若Uref不满足任一条件，则在小区域2；

同静止直角坐标系一样，确定参考矢量所处的区域后，根据临近三矢量合成原则，利用基本矢量u1,u2，u3可以确定合成参考矢量Uref，联立式(4)、式(5)，以第一扇区第一小区域为例，则就可以求出各基本矢量的作用时间依次：

则对应的第一扇区内各小区域内个基本矢量的作用时间如表2所示。

表260°坐标系下各小区域基本矢量的作用时间

区域T1T2T31T1=(1-g-h)×TsT2=g×TsT3=h×Ts2T1=(g+h-1)×TsT2=(1-h)×TsT3=(1-g)×Ts3T1=h×TsT2=(2-g-h)×TsT3=(g-1)×Ts4T1=(h-1)×TsT2=(2-g-h)×TsT3=g×Ts

同理可得其他扇区内小区域的判定和各区域内基本矢量的作用时间。

对于开关管的控制关键在于生成的PWM波形的正确与否。在生成PWM波形时，为了降低开关管的损耗，开关管的状态不能发生跳变，即开关管不能有P→N的变化。当参考电压矢量位于第一扇区第一小部分时，以七段调制为原则，则各个基本电压矢量的作用顺序：POO(T1/4)→OOO(T0/2)→OON(T2/2)→ONN(T1/2)→OON(T2/2)→OOO(T0/2)→POO(T1/4)，驱动信号示意图如图5所示。

图5A相开关管驱动信号示意图

从图5可以看出开关管VT11和VT13的驱动信号恰好为相反互补的，而开关管VT12和VT14开关管的驱动信号也为相反互补的，所以对每一相开关管的控制驱动信号只要两个，其他两个开关管的驱动信号只要取反与之相反即可，这样可以较大程度上减少工作量。

4 仿真和实验

利用MATLAB软件，在Simulink中搭建仿真模型实验平台，系统仿真模型图如图6所示，图7为具体的g-h坐标下的SVPWM算法，对文中的SVPWM算法进行仿真验证。仿真试验参数：Ud=720 V，Ts=0.6 ms，仿真时间设置为0.3 s，f=50 Hz。图8～图10为仿真波形，图11～图13为实验波形。从图8可以看出，每个周期参考电压矢量依次通过了6个扇区。图9、图12为A相相电压波形图。图10、图13为AB两相线电压波形图。实验波形图与仿真波形图相符，验证了此方法的可行性；同时，和两电平逆变器相比，三电平逆变器输出的五电平阶梯波更加逼近正弦波，验证了此方法的先进性。图11依次往下顺序为4个开关管驱动波形图，从图中可以明显看出VT11，VT13驱动波形互补，VT12，VT14驱动波形互补。

图6三电平逆变器系统仿真模型

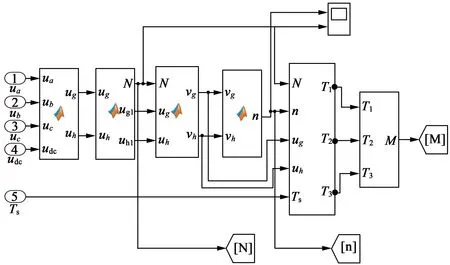
图7g-h坐标下的SVPWM算法

图8扇区判断仿真波形图

图9A相相电压波形图

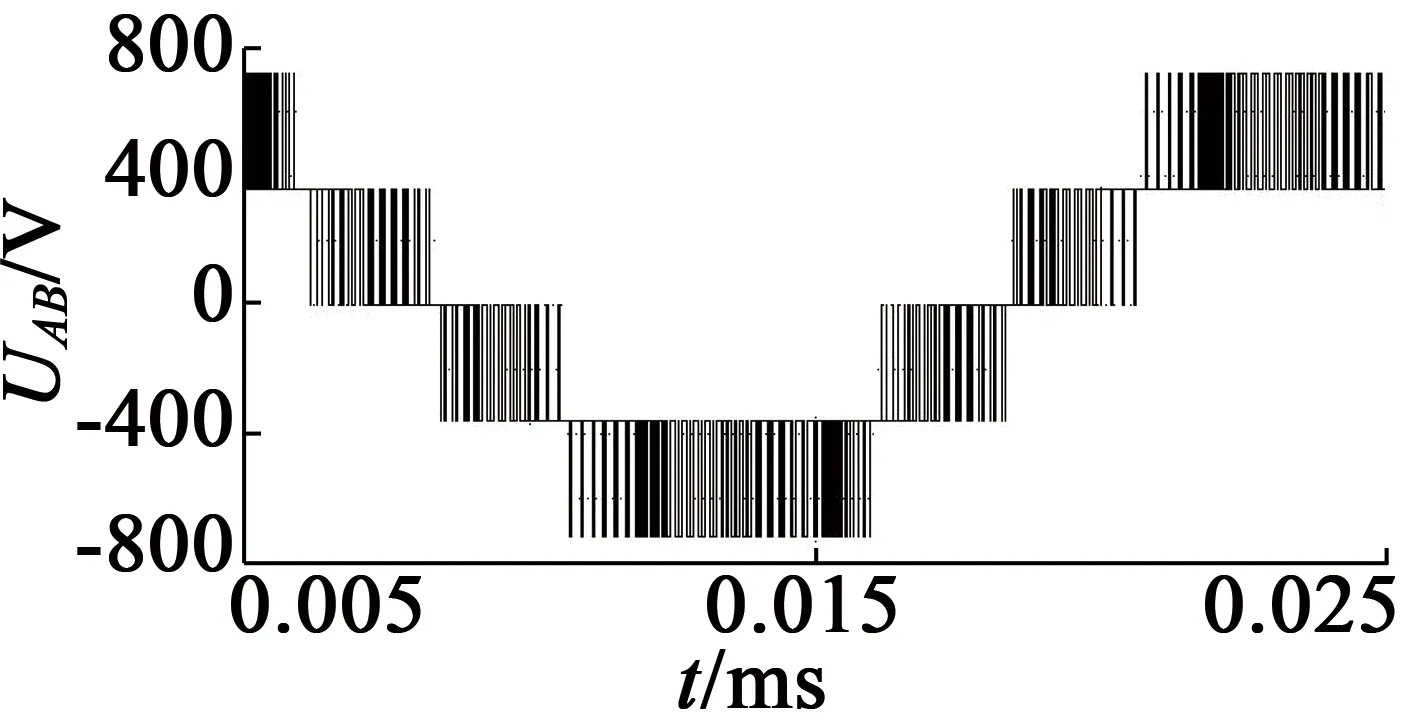
图10线电压UAB仿真波形图

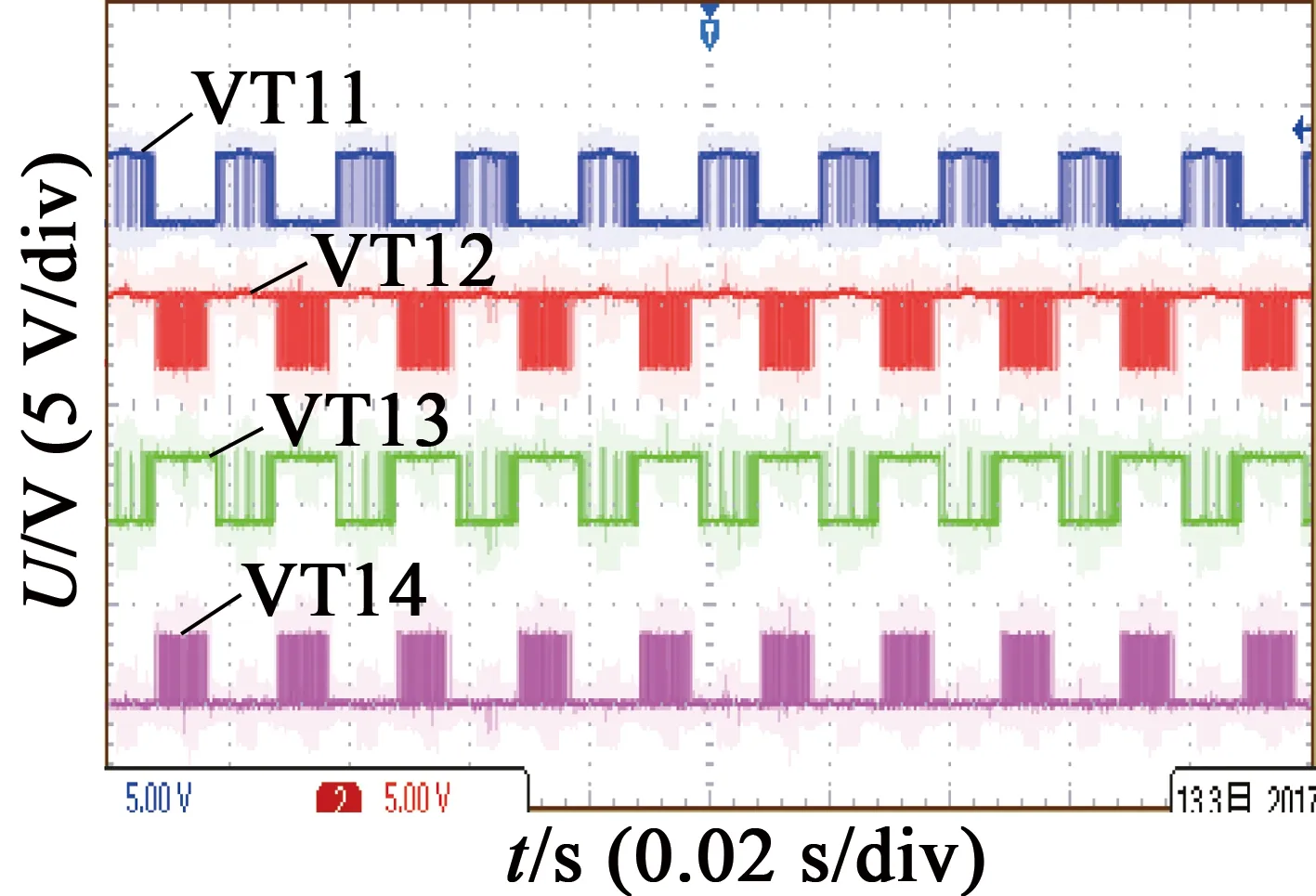
图11A相4个开关管驱动波形

图12A相相电压波形图

图13线电压UAB波形图

5 结 语

本文首先对二极管箝位型三电平逆变器的原理进行分析，其次对直角坐标系下SVPWM的算法进行分析研究，在此基础上为了克服传统SVPWM算法的大量计算问题，阐述了基于60°坐标系的空间电压调制算法，此方法在确定参考电压矢量的位置和计算基本矢量的作用时间上大大减少了计算量，并通过MATLAB仿真和硬件实验验证了其方法的正确性和可行性。

[1] 鲁金升，陈晓霖，王若羽，等.基于s函数的60°坐标系下三电平SVPWM的研究[J].电力科学与工程，2017，33(3):36-41.

[2] 董兴发，董长双，张忠国.基于第一扇区的三电平SVPWM算法[J].煤矿机械，2014，35(2):59-61.

[3] 张纯江，贲冰，王晓寰，等.基于三电平SVPWM扇区过渡问题的技术研究[J].电力电子技术，2016，50(4)：67-69，74.

[4] 何登，李春茂，华秀洁，等.一种简化三电平SVPWM方法研究[J].电力电子技术，2014，48(5):74-76.

[5] 赵辉，李瑞，王红君，等.60°坐标系下三电平逆变器SVPWM方法的研究[J].中国电机工程学报,2008,28(24):39-45.