基于电流追踪的开关磁阻电机转矩脉动抑制研究

张崇娇，沈小林

(中北大学，太原 030051)

0 引 言

开关磁阻电机是目前市场上比较有竞争力的一种新型电机，它具有电机结构简单,运行可靠,工作效率高等优点。近几年，学者们对开关磁阻电机进行深入研究，使其能够高效应用于各个领域。开关磁阻电机的转子上没有永磁体或绕组，这一特点使它在工作中有较高的可靠性，用于现场环境恶劣的场合。开关磁阻电机性能良好，可频繁正反转，调速范围广，过载能力强，工作效率高。但是由于其本身的双凸极结构，使得开关磁阻电机的噪声、振动以及转矩脉动比其他电机都要高，而转矩脉动又是振动和噪声的起因之一，所以控制开关磁阻电机的瞬时转矩并抑制转矩脉动，一直是学者们的研究目标。

近几年，学者们提出了诸多减小转矩脉动的方法，除了对传统电流斩波和开通关断角度进行优化外，还将现代控制、智能控制等先进控制方法应用进来，进行转矩脉动的高效控制。文献[1-2]提出的电流上下限斩波法，可降低导通过程中的振动和转矩脉动，但换相过程中依然有较大的瞬时转矩变化，且该方法在电机高速运行时必须提高斩波频率，这将导致功率开关器件的损耗。文献[3]针对开关磁阻电机的矩角特性，对转矩分配函数的约束条件进行研究，但它无法用一个转矩分配函数来达到各个转速、负载条件时转矩的恒定，需要通过静态矩角特性簇曲线来构建转矩分配函数簇。但准确的静态矩角特性曲线通过实验难以得到，并且由于各个厂家的开关磁阻电机参数不同，因此该方法推广难度大，受到一定的制约。文献[4-6]将转速信号、实时转矩、位置信息和电流信号作为控制器的输入量，利用神经元模糊学习算法对电流反馈补偿值进行调整，但此方法转矩闭环建立困难，实际推广意义不大。

本文用一种新方法构建转矩-电流映射。基于电机模型“转矩-位置角”平面的曲线，利用曲线拟合的数值分析方法总结不同电流下的转矩曲线簇表达式，通过这些表达式最终得到电机的控制量和参考量的完整映射函数，实现以电流控制瞬时转矩的目的。此方法适用于控制瞬时转矩，通过控制电流值，对导通周期里每个位置角度上的瞬时转矩进行控制，便于转矩曲线波峰区域和波谷区域相电流波形的调节，从而使转矩趋于恒定，实现转矩脉动的抑制。通过仿真验证了此方法的有效性。

1 基于转矩—位置角曲线拟合方程构建转矩—电流映射

1.1 转矩—位置角曲线的特点

有限元仿真时，保持转速不变，在固定位置角度上，单相通电时，转矩与产生此转矩的电流值是一一对应的，如图1所示。即在某位置角度下，转矩与电流是呈一一对应的映射关系，且在各个斩波电流下的转矩波形非常相似，转矩波形上下平移后可以基本重合。

图1各种斩波电流下的转矩—位置角度曲线

因此矩角平面内的电流—转矩曲线都是由式(1)类型[7]的曲线簇构成：

TI=f(I)+TI0(θ)

(1)

式中：曲线TI0=TI0(θ)是由2D有限元分析得到的某一参考电流下的参考矩角特性曲线；f(I)是随着电流变化，转矩T1平移的量，当I=I0时，f(I)=0。

如图2所示，进行了500～1 300 r/min转速范围内，固定开通角和斩波参考电流时电机某相瞬时转矩的仿真。

图2500 r/min～1 300 r/min转矩—位置角曲线

从图2可以看出，不同转速时，转矩波形有很大差异，这是因为绕组电感影响了电流上升速度didt，所以不同转速下必须考虑开通角，当转速升高时，应相应的提前开通角度，可以在各个转速下，分别构建以下曲线簇：

TIn=fn(I)+TI0n(θ)

(2)

式中：TI0n(θ)为转速为n时的参考矩角特性曲线表达式；fn(I)为转速为n时的转矩平移量。

这种方法把形式复杂的偏微分方程，分离变量转变为不含微积分的形式简单的函数，便于DSP中的实时计算。经过有限元计算得到的电机模型的参考转矩曲线，在一定程度上反映了磁路饱和、漏磁以及磁链曲线的非线性，比直接通过磁链方程解析计算得到的转矩值误差要小一些。

1.2 参考矩角特性曲线的获取

由式(2)可知，某转速时的参考矩角特性曲线作为先验经验在本方法中十分关键，其准确性与否关系到瞬时转矩控制的准确性。本文使用ANSYS Maxwell与ANSYS Simplorer的联合时步有限元仿真进行电机瞬时转矩的计算。

ANSYS Maxwell是最常用的电磁有限元仿真软件，但ANSYS Maxwell中自带的控制电路只能进行最基本电机运行控制，不能满足开关磁阻电机的瞬时转矩控制系统的设计[8]。ANSYS Simplorer是功能强大的机电系统设计与仿真分析软件，可以进行复杂控制系统和电路的动态仿真，所以本文采用ANSYS Simplorer搭建开关磁阻化机的控制电路，与ANSYS Maxwell进行联合有限元仿真。

2 参考矩角特性曲线的分段拟合

2.1 分段拟合的方法

本文基于电流—转矩映射的瞬时转矩控制方法中，最基本的先验数据是由有限元仿真获得的“参考矩角特性曲线”，曲线的原始数据是固定步长的一系列离散的点。由图1和图2可以看出，在一个导通周期内的瞬时转矩波形是一个较复杂的曲线，为了降低转矩-位置角曲线的曲线拟合难度，可以通过分部曲线拟合的数值分析方法，得到各个区间的TI0n(θ)的转矩函数表达式，然后构建如式(2)所示的转矩—位置角平面的曲线簇，从而得到电机的斩波电流Iref和瞬时转矩TI的映射函数。

如图3所示，在某相的一个完整导通周期内，按照转矩曲线的形状可以把转矩曲线分成5个部分。

图3相导通区间内转矩曲线的分段

[θ0，θ1]区域是电流开通区间，由于电流开通时上升速度比较快，[θ0，θ1]区域的电流参考值可以赋予定值，此区域的转矩曲线不需要拟合。

[θ1，θ2]和[θ2，θ3]区域的转矩曲线形状较相似，可以分别拟合如下：

(θ)

(3)

(4)

由于θ3之后电机转子轴线离定轴线越来越近，电感的变化减小，径向磁密接近最大，机电能量的转换减小，此时过大的电流会増加铜耗，所以θ3之后Iref也赋予定值。

所以，在实际的控制中，一个导通周期内可以分为3个区间，分别为[θon，θ2]，[θ2,θ3]，[θ3，θoff]。其中θon和θoff分别为相电流开通角度和相电流关断角度。抑制转矩脉动，可以从抑制导通时[θon,θ2]和[θ2,θ3]区域的转矩尖峰，并提高换相时的转矩波谷入手。

2.2 瞬时转矩控制的方法

转矩—位置角平面上的每个点，都可以认为在电流—转矩曲线簇上，即理想状态下，每一个瞬时转矩都对应着某个电流参考值。

在式(2)中，令TI=P，其中P为常数，则：

P=fn(I)+TI0n(θ)

(5)

式(5)为恒定转矩控制的表达式。通过转换可以得到电流I关于位置角度θ的函数，即:

(θ)]=g(θ)

(6)

式(6)的意义：为使瞬时转矩保持在定值，瞬时电流I在每一个导通位置角度上取值。因为电机开通或斩波时电流的上升速度很快，所以瞬时电流I在控制中可以当成电流斩波参考限值Iref。

式(6)是一个运算较简单的表达式，避免了传统冗繁的电磁方程计算，由于没有微积分的运算，嵌入式控制系统CPU占用的运算资源少，且比查表获取参考电流值的方法更加灵活，所以特别适合于实时瞬时转矩控制。

3 样机的转矩脉动抑制效果

以4 kW，1 000 r/min，12/8极开关磁阻电机样机为例，进行恒转矩控制。令输出转矩峰值为50 N·m，矩角特性曲线如图4所示，分别拟合T1，T2两部分区域的曲线。

图4矩角特性曲线

若使函数y=f(x)通过有限序列的资料点(xi,yi)，一般使用最小二乘法获得其拟合多项式，很多软件都能较快完成此项工作[9-10]。

本文中，相电流超前最小电感位置4°开通，超前最大电感位置3.5°关断。

3.1 T1区域(某相位置角14°～16°)

常规的电流斩波控制方式下，取Iref=25 A时，电机模型经过2D有限元计算，得到T1区域的瞬时转矩曲线T1-25(θ)，将曲线上的点经过拟合后，得到下式：

式中：Pi_25(i∈[1,7])。拟合后的曲线如图5所示。

图5斩波电流25 A时T1区域拟合转矩曲线

当Iref=26 A时，T1区域的瞬时转矩曲线T1-26(θ)经过拟合后得到表达式：

式中:Pi_26为常数(i∈[1,7])。

同理，分别取Iref为20 A,21 A,…,30 A，得到T1-I的曲线簇，发现拟合后的多项式除了常数P1_I各不相同，其余的多项式系数Pi_I是几乎相同的，即矩角平面内，各个电流下转矩曲线的形状是一定的，但沿T轴的上下位移量不同。

分别令T1-21-T1-20，T1-22-T1-21，T1-23-T1-22，…，T1-30-T1-29，即：

E(m)=Tm+1-Tm

(9)

式中：m∈[20,29]。

E(m)变化非常小，不妨认为每条转矩曲线之间的上下的位移量是相同的，在[20,29]的区间里可以取E(m)≈k，k为常数，k可取算术平均值:

以图4中25 A曲线为参考曲线，由式(5)、式(8)、式(10)，曲线簇可表示：

T1_I=k(25-I)+T1_25(θ)

(11)

令T1-I=50，则可得到恒转矩控制时电流与位置角的对应关系式：

开关磁阻电机运行时的斩波限值参考电流Iref仅通过式(12)的计算就可以取得，比较方便。

3.2 T2区域(某相位置角16°～20°)

同区域T1，在位置角16°～19.9°时，经过有限元计算得到的曲线，将曲线上的点经过公式拟合后，可得到表达式:

T2_25(θ)=q1_25+q2_25θ0.5+q3_25θ+

q4_25θ2+q5_25θ3+q6_25θ4

(13)

式中：q1_25，qi_25为常数(i∈[2,7])，拟合后的曲线如图6所示。

图6斩波电流25 A时T2区域拟合转矩曲线

同理，以25 A曲线为参考曲线，T2区域曲线簇可表示：

T2_I=k(25-I)+T2_25(θ)

(14)

令T2-I=50，则可得到恒转矩控制时参考电流关于位置角的变化曲线：

综上所述，式(12)和式(15)表达了保持恒定转矩50 N·m时在某相导通区间内斩波参考电流取值。

4 有限元仿真

按照本文的恒定瞬时转矩控制策略进行单相绕組通电的有限元仿真，得到的瞬时转矩如图7所示。

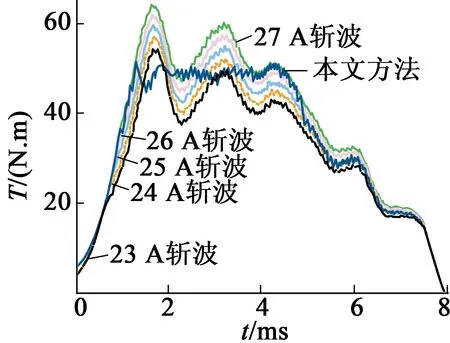
图7单相绕组通电时的瞬时转矩

按照本方法进行恒定瞬时转矩控制的仿真结果，与其余23～27 A的传统电流斩波控制获得瞬时转矩相比，其转矩脉动获得了较好的抑制。

三相轮流导通时，瞬时转矩和电流波形如图8所示。电机正常运行时转矩尖峰得到了有效削弱，在导通区间瞬时转矩基本保持平稳。但是与单相通电的仿真结果还是有所不同，这是因为此时的瞬时转矩是三相合成转矩，相邻关断或开通相产生的转矩会对本方法的效果产生一定影响。

图8三相轮流导通时的瞬时转矩

通过仿真数据计算可知，保持开通角和关断角相同，传统电流斩波时样机的转矩脉动率为72%，采用本方法后转矩脉动率为55%，降低了23.6%。

5 结 语

本文介绍了一种新的基于电流—转矩映射的瞬时转矩控制方法，通过有限元仿真获得电机模型的“转矩—位置角”平面的曲线簇，通过曲线拟合的数值分析方法构建不同电流的瞬时转矩曲线簇表达式，从而得到电机的斩波限流值和瞬时转矩的关系式，可以按照系统对瞬时转矩的要求实时改变电流。

这种方法的优点在于电流—转矩映射控制函数简洁，没有复杂的微积分运算，计算量巧少，适合于实时控制，有利于降低嵌入式控制系统的资源占用率。

但是本方法也存在一些问题，应在今后的研究中继续改进。如：换相时相邻的导通或关断相输出的转矩对瞬时转矩有较大的影响，后续的工作应考虑相邻两相的转矩分配，减小换相时的转矩脉动；在实际的应用中，应充分考虑IGBT的通断频率，本方法在电机低速时效果明显，但是高速时需要提高斩波频率以获得合适的电流波形，对IGBT或MOSFET的通断频率有较高要求。

[1] 王宏华．开关型磁阻电动机调速控制技术[M]第1版.北京：机械工业出版社，1995．

[2] 王旭东，王喜莲，王炎,等．开关磁阻电动机电流双幅值斩波控制[J]．中国电机工程学报,2000,20(4):83-86.

[3] KIMC H,HA I J.A new approach to feedback——linearizing control of variable reluctance motors for direct-driveapplications[J].IEEE Transactions on Control System Technology,1996,4(4):348-362.

[4] LUIS O A P Henriques,LUIS G B Rolim,Walter I Suemitsu.Torque ripple minimization in a switched reluctance drive by neuro—fuzzy compensation[J].IEEE Transactions on Magnetics,2000,36(5):3592-3594.

[5] 张舒辉.用于开关磁阻电机转矩脉动抑制的新型功率变换器研究与设计[D].镇江:江苏大学,2016.

[6] 张玉光.开关磁阻电机非线性建模及转矩脉动抑制技术的研究[D].哈尔滨:哈尔滨理工大学,2014.

[7] CHANG Y C,LIAW C M. Establishment of a Switched-Reluctance Generator-Based Common DC Microgrid System[J].IEEE Transactions on Power Electronics, 2011, 26(9):2512-2527.

[8] 马云龙.开关磁阻电机转矩脉动抑制的研究[D].杭州:浙江大学,2014.

[9] 刘涛,吴忠,吕昊暾.开关磁阻电动机转矩分配策略研究[J].微电机,2013,46(7):11-15.

[10] INANC N,OZBULUR V.Torque ripple minimization of a switched reluctance motor by using continuous sliding mode control technique[J].Electric Power Systems Research,2003,66(3):241-251.