基于极端学习机的网络流量预测模型

鲁华栋， 时磊

(河南工业职业技术学院 1.网络管理中心，2.电子信息工程系，南阳 473000)

0 引言

随着互联网规模的不断增大，每一个小时的网络业务量不断增多，增加了网络拥塞频率，网络流量预测可以为网络管理提供有有价值的参考意见，设计高精度、速度快的网络流量预测模型十分关键[1-3]。

网络流量预测的研究可以分为两个阶段：传统阶段和现代阶段，传统阶段主要有时间序列法、多元线性回归等[4-6]，它们假设网络流量呈现线性变化规律，建模速度快，然而网络流量受到多种因素影响，具有时变性、混沌性等，预测精度低，预测结果不可靠[7]。现代阶段主要采用机器学习算法对网络流量进行建模和预测，其中神经网络应用最为广泛，预测精度得到了一定提升[9-11]。极端学习机(extreme learning machine，ELM)属于新前馈神经网络，建模效率要高于其它神经网络，可以应用于非线性的网络流量预测建模[12]。标准限学习机采用随机确定输出权值，泛化能力差，易出现过拟合缺陷。因此有学者提出了一种改进极端学习机(Regularized ELM，RELM)，泛化能力得到了改善，但RELM只能对网络流量进行离线建模，无法满足网络流量的在线预测要求[13]。为此，有学者提另一种改进极端学习机(online sequential extreme learning machine，OS-ELM)，但计算复杂度高，建模效率低[14]。

为了更加准确地对网络流量进行预测，提出了一种改进极端学习机(Improved ELM，IELM)的网络流量预测模型，并通过网络流量数据的预测实验验证其可行性。结果表明，与其它网络流量预测模型相比，改进极限学习的网络流量预测结果更加可靠，可以更加准确描述网络流量将来的变化趋势，提高了网络流量的预测精度。

2 极端学习机算法及改进

(1)

相关参数见[12]。

对式(1)直接进行求解十分复杂，难以实现，为此引入拉格朗乘子,得到式(2)。

(2)

式中，Hk为神经元矩阵,w为权值。

对式(2)进行求偏导，同时设偏导数为零，那么可以得到式(3)。

(3)

式中，I为单位矩阵

极端学习机的回归模型为式(4)。

(4)

式中，t和x分别为输入和输出。

在极端学习机的回归过程中，实际就是找到βk的值，但该过程包括矩阵求逆运算，使得极限学习的学习比较费时。为此本文提出一种改进极端学习机(IELM)。

设根据时间序列Sk已得到输出权值βk，当有训练样本加入时，输出权值变为式(5)。

(5)

(6)

根据矩阵求逆引理得到Pk的递推表达式为式(7)。

(7)

联合式(5)和式(6)得到βk的递推表达式为式(8)。

(8)

根据Cholesky分解方法求解βk，则有式(9)。

(9)

那么βL求解过程可被转化为求解形如式(10)的线性方程，加快学习速度为式(10)。

ALβL=bL

(10)

对AL进行Cholesky分解得到式(11)。

(11)

式中，SL是一个三角矩阵,如式(12)。

最后βL为

(12)

其中，sij表示SL中不为零的元素；fi为式(13)。

(13)

3 改进极限学习网络流量预测模型

3.1 混沌理论

设原始网络流量数据集：{x(i),i=1,2,…,n}，根据混沌理论可以变为一个多维时间序列为：X(t)={x(t),x(i+τ),…,x(i+(m-1)τ)，其中，τ表示延迟时间，分析一对样本点：X(i)和X(j)，那么两者的距离rij(m)为[15]式(14)。

(14)

关联积分计算公式为式(15)。

(15)

式中，r为阈值。

将网络流量数据{x(i),i=1,2,…}可划分成t个子时间序列，则有式(16)。

(16)

式中，Cl表示第l个子序列的相关积分。

极小值点的计算公式为式(17)。

(17)

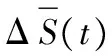
令式(18)。

(18)

式中，Xi(m+1)为重构后的i个向量；Xn(i,m)(m+1)为的Xi(m+1)最近邻。

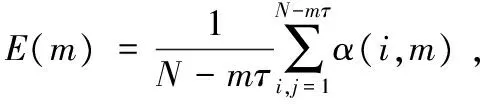
3.2 改进学习机的网络流量预测模型的工作过程

Step1:收集网络流量历史时间序列数据，对其归一化操作，具体为式(19)。

(19)

式中，x(i)和x′(i)分别为原始和归一化后的值，max()和min()分别为最大值和最小值。

Step2: 确定最佳τ和m，对原始网络流量数据重构，建立IELM的学习样本。

Step3: 确定IELM输入权值αk及隐含层偏差bk值，并将网络流训练集输入到IELM进行训练。

Step4: 计算隐含层输出矩阵H。

Step5: 计算输出层权值βk。

Step6: 将βk代入式(4)建立网络流量预测模型，并对测试集进行验证，根据结果对IELM的性能进行分析。

4 网络流量预测模型的性能测试

4.1 实验环境及数据

为了分析改进极端学习机的性能，选择标准测试数据集http://newsfeed.ntcu.net/～news/2015/的每小时流量作为实验对象，它们如图1所示。

图1 实验数据

采用Intel 4核 3.0GHz CPU，32 GB RAM，Windows 10系统上作为实验平台，采用VC++6.0编程实现实验。

4.2 数据混沌处理

采用混沌理论对图1中的实验数据进行分析，得到τ和m变化曲线,如图2所示。

可以发现，最佳τ=5，m=5，这样表示网络流量数据时间上有一定的关联性，通过相空间重构可以挖掘它们之间联系，建立极端学习机的训练样本和测试样本。

4.3 结果与分析

选择文献[13]的改进极端学习机、标准学习机进行对照测试，并采用RMSE、MAPE对模型的性能进行分析，具体为式(20)、式(21)。

(20)

(21)

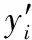
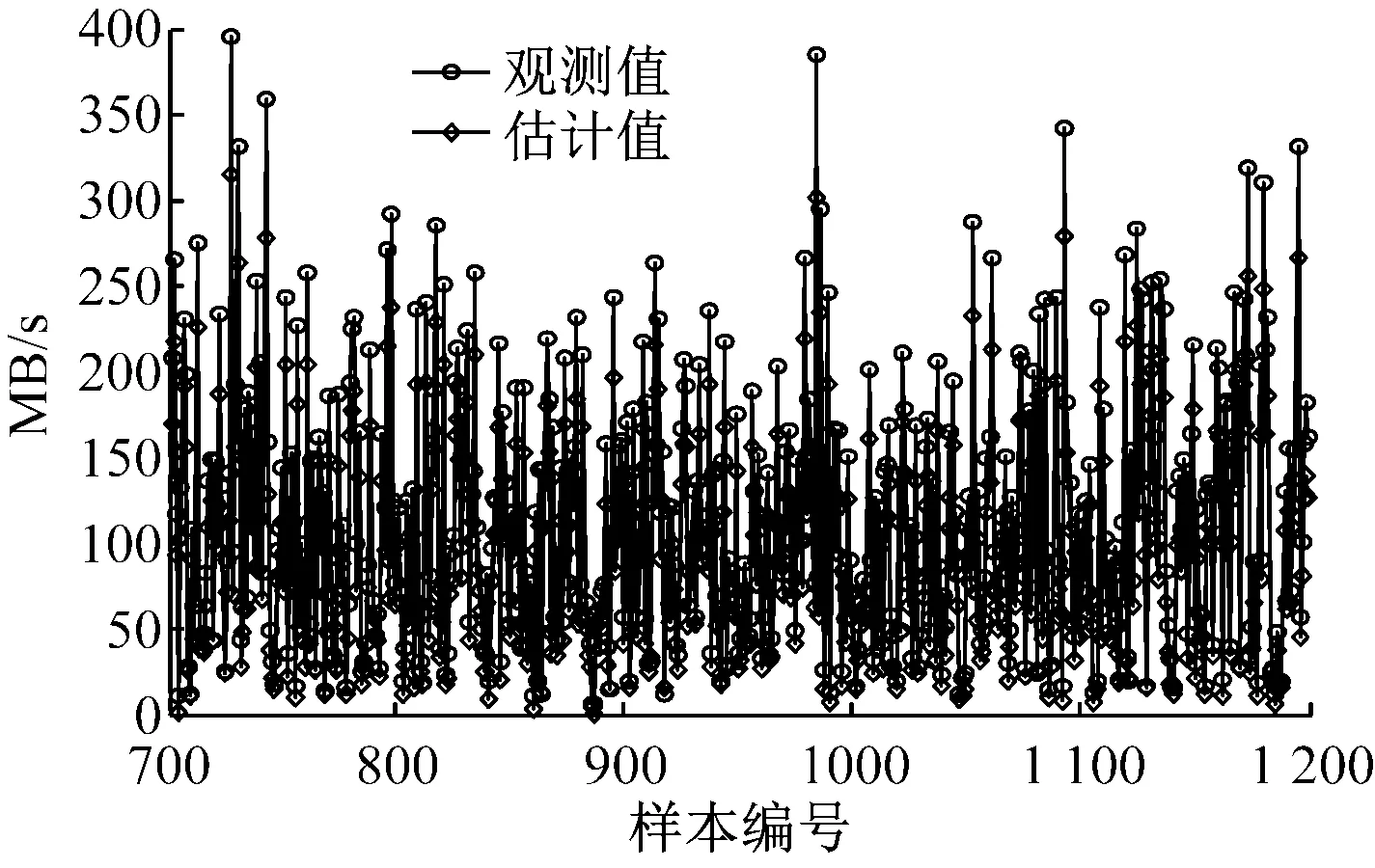
IELM的网络流量一步预测结果如图3所示。

(a) τ

(b) m

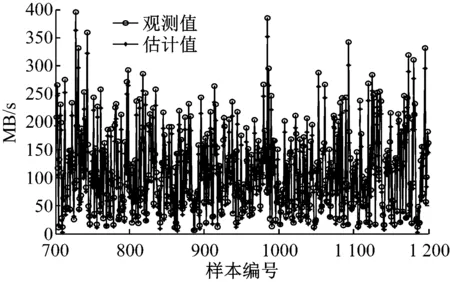
(a) 预测结果

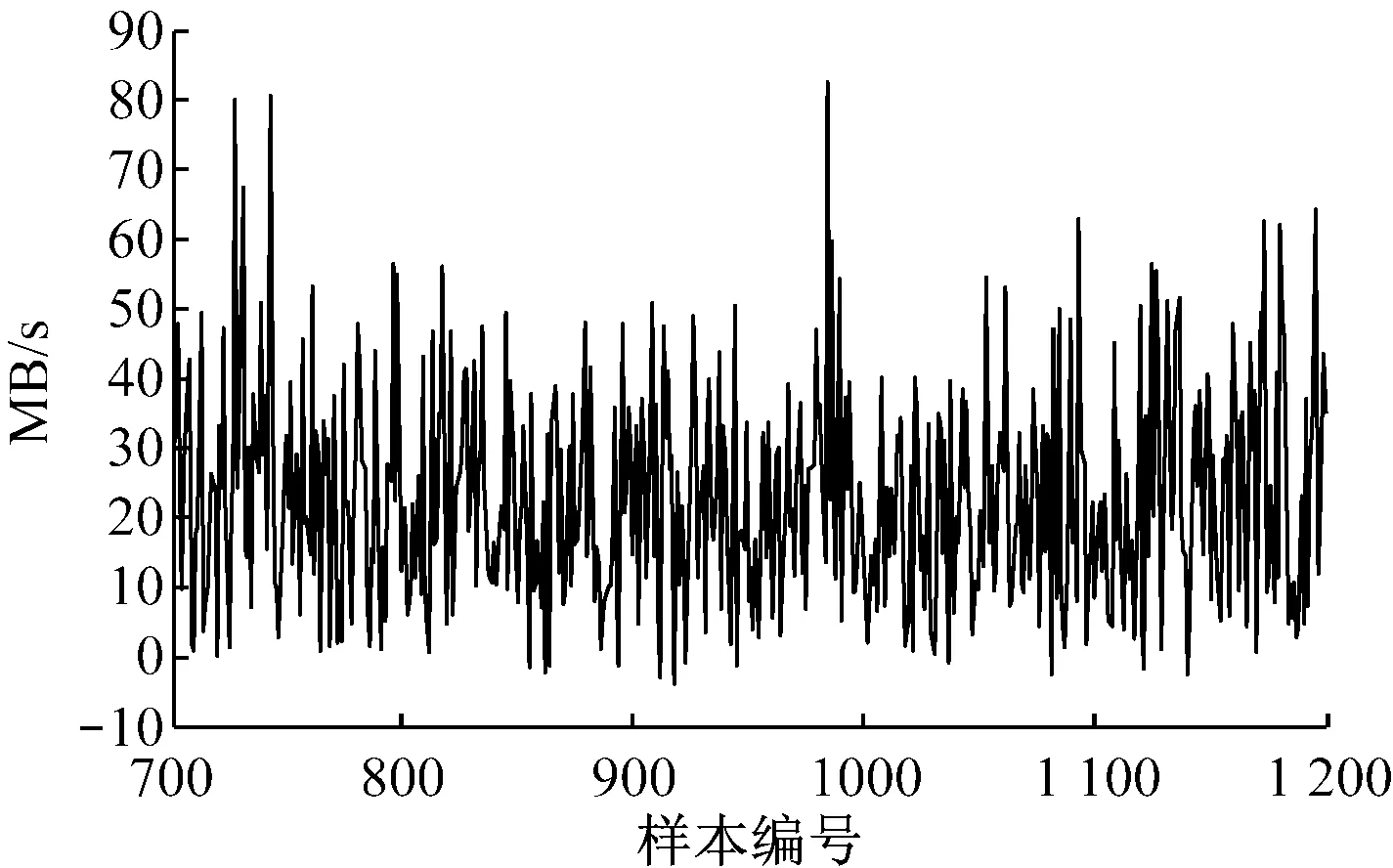
(b) 预测偏差

可以清楚看出，一步测精度高，误差波动平稳，说明将IELM用于网络流量建模与预测是可行的，预测结果可靠。

预测建模主要对网络流量将来变化趋势进行跟踪，因此进行多步预测性能分析，2步骤预测结果,如图4所示。

可以发现，预测步长增加，预测误差随之增加，预测精度相应降低，但是预测精度仍然很高，说明IELM具有较好的泛化性能。

统计所有模型的预测误差，如表1所示。

从表1的预测误差可以知道

(a) 预测结果

(b) 预测偏差

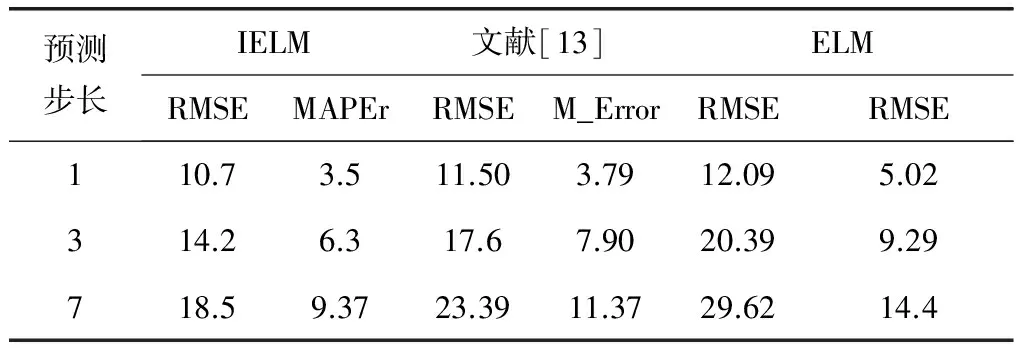
预测步长IELM文献[13]ELMRMSEMAPErRMSEM＿ErrorRMSERMSE110．73．511．503．7912．095．02314．26．317．67．9020．399．29718．59．3723．3911．3729．6214．4

(1) 因为不能在线性对网络流量进行建模，随着预测步长增大，ELM的网络流误差增加幅度比较大，过拟合现象出现的概率增加。

(2) 相对于ELM，IELM和文献[13]的网络流量预测结果得到了相应改善，降低了网络流量的预测误差，因为IELM和文献[13]改进了训练方式，解决了ELM存在的局限性，使网络流量的预测结果更优。

(3) 与文献[13]相比，IELM获得出更高的网络流量预测精度，这因为IELM通过新样本的加入，模型参数进行了动态更新，更好描述网络流量最新的状态，预测误差显著减少，网络流量的预测准确性始终比较高。

5 总结

网络流量与许多因素相关，具有比较明显的混沌性，为了加快网络流量建模速度，获得更优的预测结果，提出了改进极端学习机的网络流量混沌预测模型，具体网络流量预测结果表明，改进极端学习机可以准确把握网络流量的变化趋势，网络流量的预测结果可靠，预测结果而且要优于其它网

络流量预测模型，从而有助于网络流量的管理，有效降低网络拥塞的频率。

[1] 田中大,李树江,王艳红,等. 经验模式分解与时间序列分析在网络流量预测中的应用[J]. 控制与决策, 2015, 30(5): 905-911.

[2] 王升辉, 裘正定. 结合多重分形的网络流量非线性预测[J]. 通信学报, 2007, 28(2): 45-57.

[3] 邱艳,张洪. 一种有效的网络流量预测算法[J]. 成都大学学报(自然科学版), 2016, 35(2): 150-152.

[4] Chen Yuehui, Yang Bin, Meng Qingfang. Small-time scale network traffic prediction based on flexible neural tree [J]. Applied Soft Computing, 2012, 12(1): 274-279.

[5] 高波,张钦宇,梁永生,等. 基于EMD及ARMA的自相似网络流量预测[J]. 通信学报,2011,32(4):47-56

[6] 田中大,高宪文,李树江,等. 遗传算法优化回声状态网络的网络流量预测[J].计算机研究与发展,2015,52(5):1137-114.

[7] 王雪松,赵跃龙. 遗传算法优化延迟时间和嵌入维的网络流量预测[J].计算机工程与应用, 2014,50(12):66-70.

[8] 唐舟进,彭涛,王文博. 一种基于相关分析的局域最小二乘支持向量机小尺度网络流量预测算法[J].物理学报, 2014, 63(13):130504-130514.

[9] 杨雷,李贵鹏,张萍. 改进的Wolf步预测的网络异常流量检测[J]. 科技通报,2014,30(2):47-49.

[10] 李振刚.基于高斯过程回归的网络流量预测模型[J]. 计算机应用,2014, 34(6):1251-1254.

[11] 李明迅，孟相如，袁荣坤等. 融合提升小波降噪和LSSVM的网络流量在线预测[J]. 计算机应用，2012，32(2): 340-342.

[12] 张弦,王宏力.基于贯序正则极端学习机的时间序列预测及应用[J].航空学报,2011,32(7):1302-1308.

[13] Liu Nan, Wang Han. Ensemble based extreme learning machine[J].IEEE Signal Processing Letters, 2010, 17(8):754-757.

[14] Lan Yuan, Soh Yengchai, Huang Guangbin. Constructive hidden nodes selection of extreme learning machine for regression [J]. Neurocomputing, 2010, 73(16):3191-3199.

[15] 张涛,张颖江. 基于矢量空间重构的网络流量预测算法[J]. 计算机科学, 2016, 43(7): 111-115.