一种非线性PID控制的制氧空调系统控制算法设计

吴晓甦

(杭州市城市建设投资集团有限公司，杭州 310003)

0 引言

改善密闭室内空气质量和提高室内舒适度最有效的方法是采用具有制氧功能的空气净化系统。空气净化系统具有净化污染物和调节室内温湿度的功能，净化的主要成分包括粉尘、颗粒物、甲醛、苯和挥发性有机化合物等污染物。

制氧空气净化系统是典型的多输入多输出，大滞后，在运行过程中所受干扰多的非线性系统，传统PID控制技术难以取得良好的控制品质[1]。目前，空气净化系统广泛应用PID控制与其它控制技术相结合的控制技术。梁延东等[2]提出了单神经元技术与自适应PID控制相结合的控制技术，通过搭建仿真平台来验证系统的控制质量和控制精度，取得了较好的实验效果，但该控制技术未应用到实际工况中，难以确定其控制方案的可行性。邱黎辉等[3]提出模糊PID控制方案，通过验证证明了模糊PID控制比传统PID控制具有更好的控制效果，但对于多输入的复杂系统，该控制方案难以保证系统的稳定性和可靠性。李桂梅等[4]将神经网络算法引入空气净化系统中，但在实际验证中，对于时变的非线性系统难以对其固定参数进行优化，系统的控制精度受到一定的影响。闫秀英等[5]提出了一种基于改进Ziegler-Nichols参数整定方法的自校正PID控制器，引入带遗忘因子的最小二乘实时参数估计算法和增量式PID控制算法。通过仿真实验，系统具有较强的实时参数估计和自校正能力。

本文对现有的空气净化系统从净化技术和制氧控制技术两方面进行优化改进，提出了一种基于非线性PID控制的空气净化系统。

2 非线性PID控制算法设计

2.1 非线性PID控制构造

PID控制的数学模型,如式(1)。

(1)

KP为比例参数，KI为积分参数，KD为微分参数，e(t)为系统误差，u(t)为控制器的输出。

非线性PID控制的数学模型,如式(2)。

(2)

其中：KP[e(t)]为非线性比例参数，KI[e(t)]为非线性积分参数，KD[e(t)]为非线性微分参数，e(t)为系统误差，u(t)为控制器的输出。

当系统出现误差e(t)时，非线性比例参数影响控制器的输出u(t)，比例参数越大，系统的响应时间越短，但系统稳定性变差；非线性积分参数可消除系统的稳态误差，降低最大超调量；非线性微分参数能够提高控制系统的稳定性和快速性，控制系统偏差波动的趋势，避免被控对象的严重超调。

2.2 增益参数非线性优化

系统通过非线性函数对比例参数KP、积分参数KI、微分参数KD进行非线性转换，根据系统偏差e(t)修改各个参数，生成3个函数KP[e(t)]、KI[e(t)]、KD[e(t)]替代PID控制中的比例参数KP、积分参数KI、微分参数KD。通过对系统阶跃响应曲线的分析，得到满足系统性能要求非线性化函数，并确定优化改进后的非线性PID控制的模型。系统阶跃响应曲线,如图1所示。

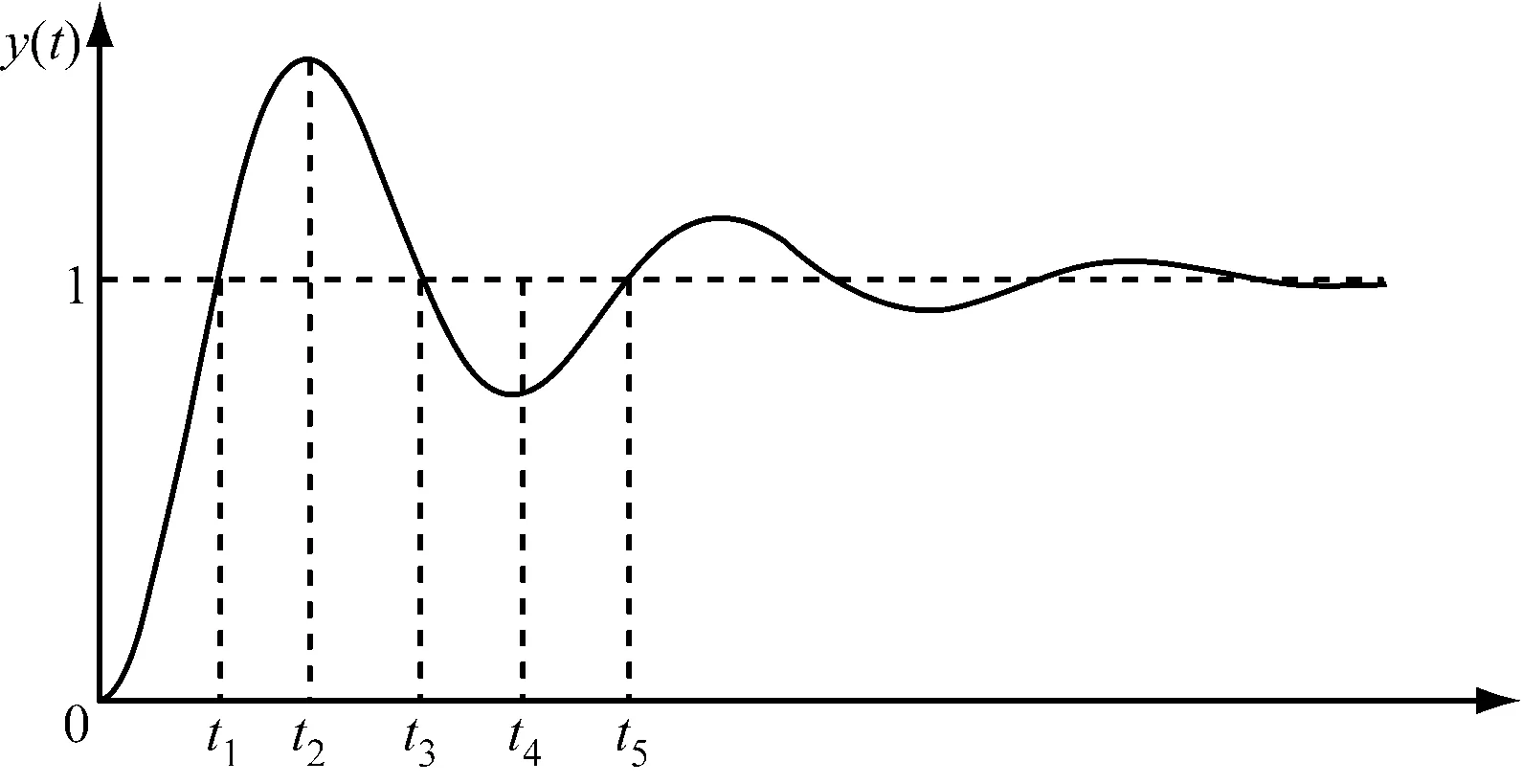
图1 系统阶跃响应曲线

2.2.1 比例函数非线性化

根据系统阶跃响应曲线变化趋势，分段比较非线性PID控制器比例增益参数的变化趋势。比例参数KP[e(t)]的变化趋势,如表1所示。

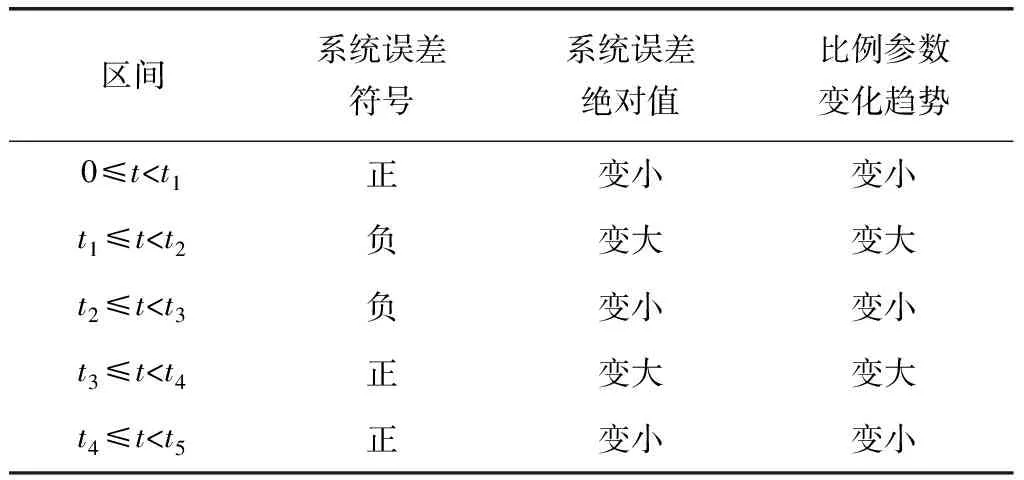
表1 比例参数变化趋势

根据表1可知，当系统响应曲线离稳定值较远时，的绝对值应逐渐增大；当响应曲线离稳定值较近时，的绝对值应逐渐减小。

根据上述规律，我们选用双曲正割函数，来构造非线性函数。双曲正割函数,如式(3)。

KP[e(t)]=ap+bp{1-sech[cp(e(t)]}

(3)

其中：ap、bp、cp为正实常数，ap的值影响KP[e(t)]的最小值，bp的值影响KP[e(t)]的变化范围，cp的值影响KP[e(t)]变化的速率。当系统误差为零时，比例增益KP[e(t)]为最小值ap，当系统误差趋近于无穷大时，比例增益KP[e(t)]为最大值ap+bp。

2.2.2 积分函数非线性化

根据系统阶跃响应曲线变化趋势，分段对比非线性PID控制器积分参数的变化趋势。积分参数KI[e(t)]变化趋势,如表2所示。

根据表2可知，非线性化后的积分参数的变化趋势和系统误差的变化趋势相反，且始终为正值。用双曲正割函数构造非线性函数,如式(4)。

KI[e(t)]=aI+bIsech[cIe(t)]

(4)

其中：aI、bI、cI为正实常数，aI的值影响KI(e(t))的最小值，bI的值影响KI[e(t)]的变化范围，cI的值影响KI[e(t)]变化的速率。当系统误差为零时，积分参数KI[e(t)]为最大值aI+bI，当系统误差趋近于无穷大时，积分参数KI[e(t)]为最小值aI。

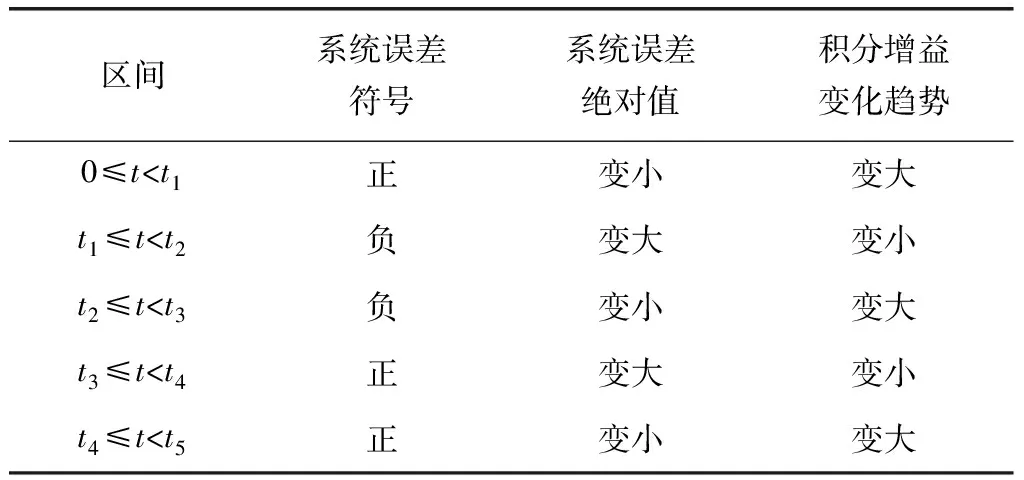
表2 积分参数变化趋势

2.2.3 微分函数非线性化

根据系统阶跃响应曲线变化趋势，分段比较非线性PID控制器微分参数的变化趋势。微分参数KD[e(t)]的变化趋势,如表3所示。

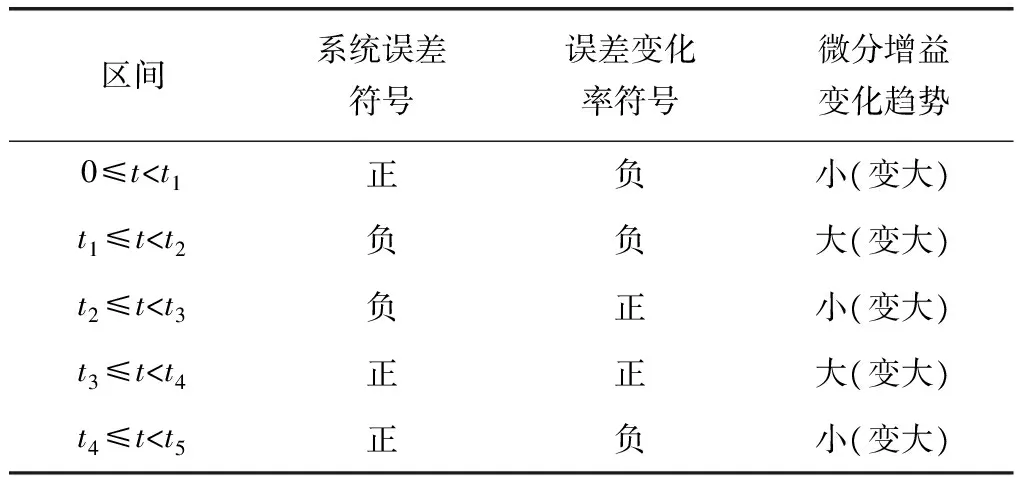
表3 微分参数变化趋势

用双曲正割函数构造非线性函数,如式(5)。

KD[e(t)]=aD+bD/{1+cDexp[dD×e(t)]}

(5)

其中：aD、bD、cD、dD为正实常数，aD的值影响KD[e(t)]的最小值，dD的值影响KD[e(t)]变化的速率。微分参数KD[e(t)]最大值为aD+bD，最小值为aD，当系统误差为零时，KD[e(t)]为aD+bD/(1+cD)。

2.3 氧气浓度非线性PID模型建立

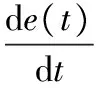
根据传统PID控制的参数值，通过调试和修正，设置非线性增益函数的限值，其中上限为传统PID控制参数值的2到3倍，下限为传统PID控制参数值的1/3到1/2，设置cP、cI、cD、dD初始值为1，得到非线性增益函数初始aP、aI、aD、bP、bI、bD的值和相关参数的变化区间：KP[e(t)]∈[1.1,3.6]，KI[e(t)]∈[0.02,0.12]，KD[e(t)]∈[2,8]

当采样氧气含量位于最大允许误差范围22%±1%时，参数变化区间为KP[e(t)]∈[1.1,2.1]，KI[e(t)]∈[0.07,0.12]，KD[e(t)]∈[4,6]。

(1)KP[e(t)]的非线性化函数

比例增益函数最大值aP+bP=3.6，最小值aP=1.1。可得aP=1.1，bP=2.5。当采样氧气含量位于最大允许误差范围22%±1%时，KP[e(t)]=aP+bP×{1-sech[cP(e(t)]}=2.1，可得cP=1.1。氧气浓度的非线性比例增益函数,如式(6)。

KP[e(t)]=1.1+2.5×{1-sech[1.1×(e(t)]}

(6)

(2)KI[e(t)]的非线性化函数

积分增益函数最大值aI+bI=0.12，最小值aI=0.02。可得aI=0.02，bI=0.1。当采样氧气含量位于最大允许误差范围22%±1%时，KI[e(t)]=aI+bIsech[cIe(t)]=0.07，可得cI=1.3。氧气浓度的非线性积分增益函数,如式(7)。

KI[e(t)]=0.02+0.1×sech[1.3×e(t)]

(7)

(3)KD[e(t)]的非线性化函数

微分增益函数最大值aD+bD=8，最小值aD=2。可得aD=2，bD=6。

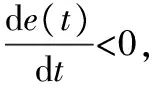
KD[e(t)]=2+6/{1+exp[0.7×e(t)]}

(8)

将比例、积分和微分增益函数式(3)、(4)、(5)代入非线性PID控制的数学模型(2)中，可得室内氧气浓度非线性PID控制的数学模型,如式(9)。

(9)

3 仿真分析

3.1 传统PID空气净化系统模型建立

通过Simulink平台搭建系统模型，对空气净化系统中的被控参数进行仿真分析。在Simulink中建立传统PID空气净化系统仿真模型，如图2所示。

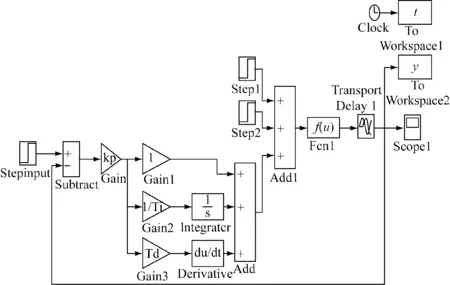
图2 传统PID空气净化系统仿真模型

3.2 非线性PID空气净化系统模型建立

本文利用Simulink模块和S函数来建立非线性PID空气净化系统仿真模型，如图3所示。

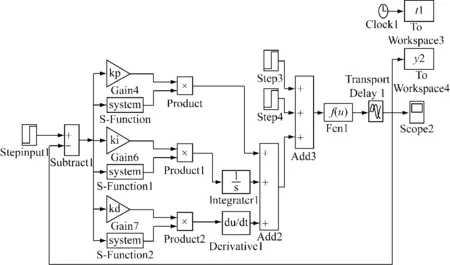
图3 非线性PID空气净化系统仿真模型

3.3 氧气浓度传递函数建立

室内氧气主要来源于室外制氧机组和室外净化过滤机组，按照守恒定律：室内氧气浓度的变化量等于单位时间进入室内的氧气量减去排出的氧气量。等量如式(10)—式(12)。

(10)

Q0-Q3=Gmax×K2×(t0-tn)

(11)

Gmax=V×Nmax

(12)

其中：Q0为制氧机组中的氧气量，Q1为净化过滤机组中的氧气量，Q2为室内救援人员消耗的氧气量，Q3为排风带出的氧气量，Gmax为最大换气量，t0为制氧机组的氧气浓度，tn为排风氧气浓度，K1、K2为损耗系数，V为空气净化空间体积，Nmax为最大换气次数。

对式(10)、(11)进行化简，得到式(13)。

(13)

其中：T为时间常数、K为放大系数、tf为折算后的新风氧气浓度。

将上述为微分方程经过拉布拉斯变换，得到室内氧气浓度的传递函数近似为式(14)。

(14)

仿真实验中，设定空气净化空间为30 m3，最大换气次数为6/h。不考虑氧气浓度在时间上的滞后，得到K=30，T=2.4。因此，室内氧气浓度的传递函数,为式(15)。

(15)

3.3 氧气浓度仿真结果分析

在仿真环境中，设置初始氧气浓度为最低限值17%，要求空气净化系统将室内氧气浓度控制在22%。根据图2和图3所示的模型对氧气浓度进行仿真分析，PID控制氧气浓度曲线图,如图4所示。

非线性PID控制氧气浓度曲线图,如图5所示。

根据图4和图5所示，系统采用传统PID控制，响应时

间约为4.5 min，调整时间约为50 min，最大超调量约为2.62。系统采用非线性PID控制，响应时间约为9.5 min，调整时间约为20 min，最大超调量约为0.46。将两种控制系统的响应列表对比，如表4所示。

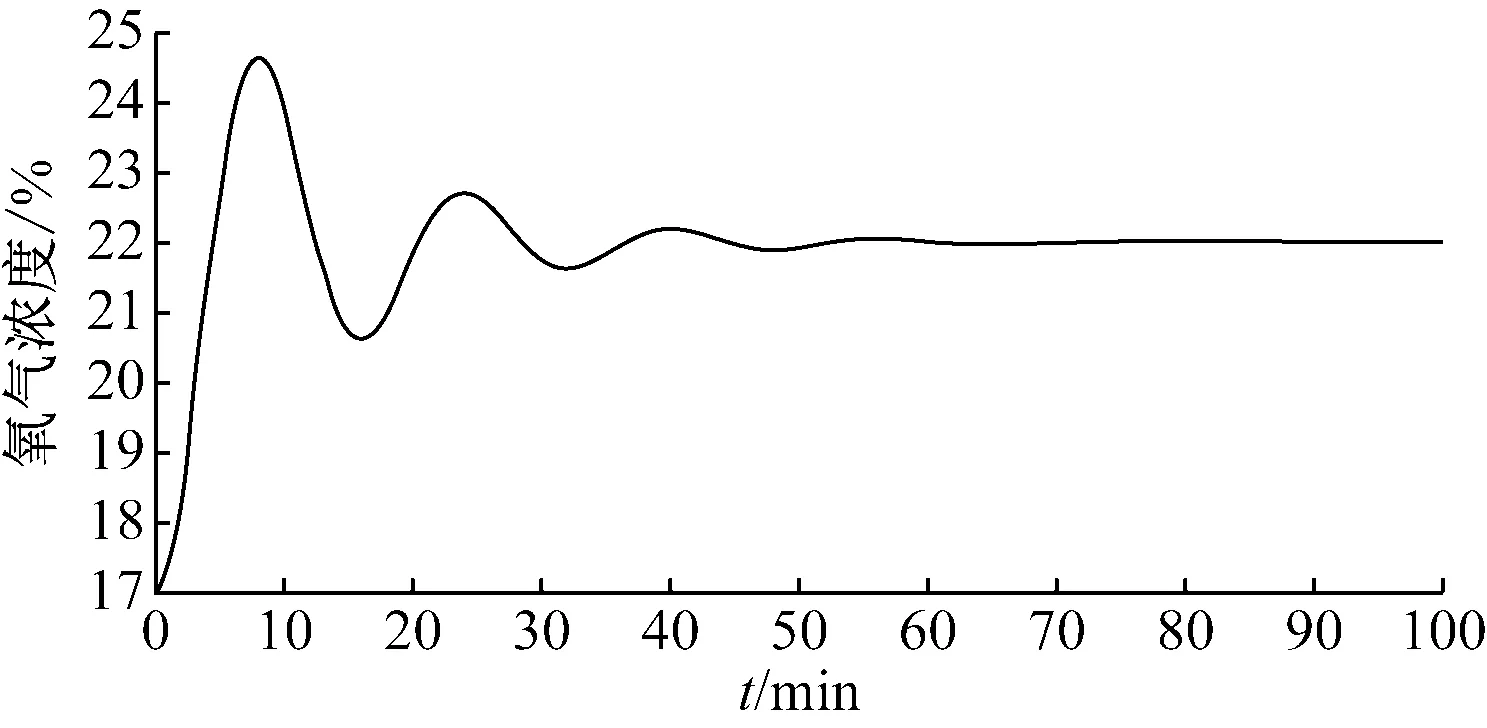
图4 PID控制氧气浓度曲线图

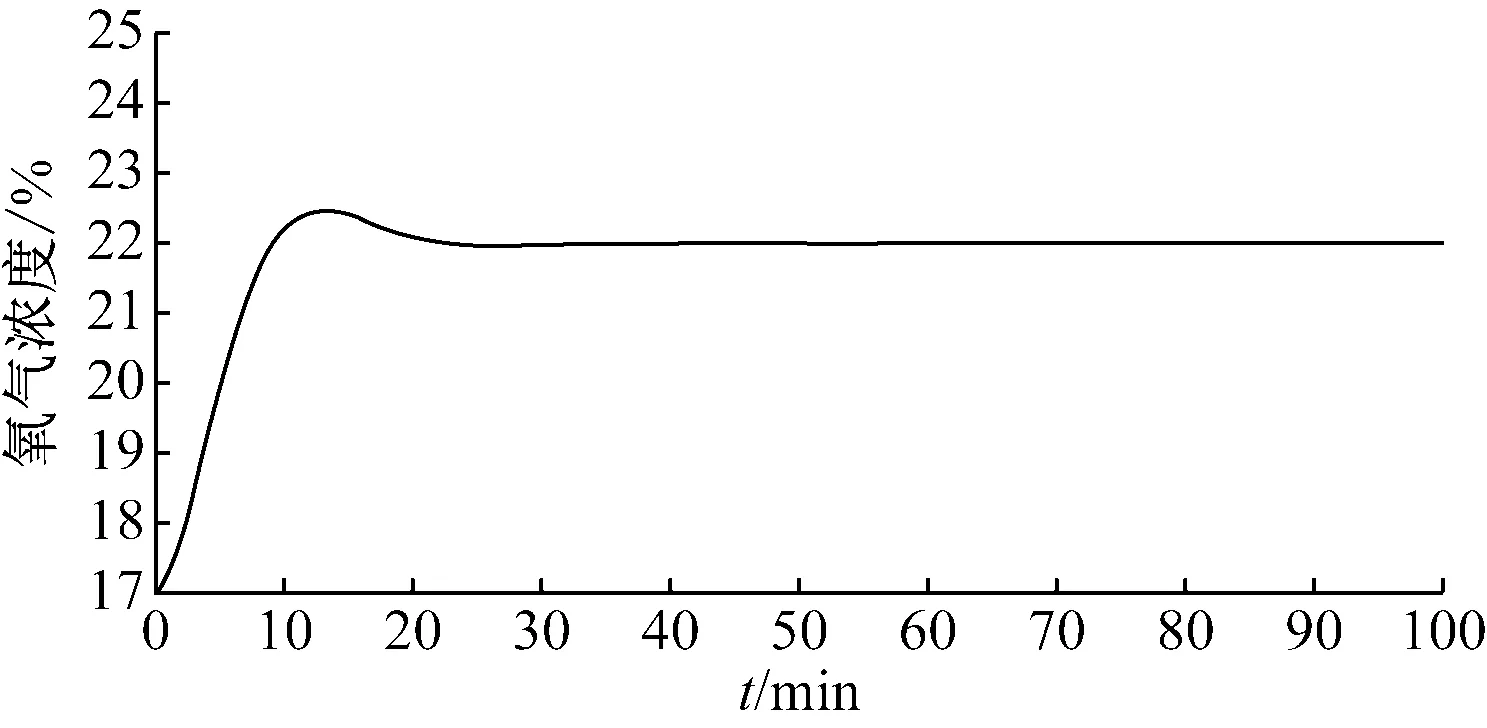
图5 非线性PID控制氧气浓度曲线图

控制系统响应时间调整时间最大超调量传统PID控制4．5min50min2．62(11．9%)非线性PID控制9．5min20min0．46(2．1%)

根据表4可以看出：系统采用非线性PID控制的最大超调量比采用传统PID控制的最大超调量明显下降，系统到达稳定值的调整时间大幅度缩短。虽然非线性PID控制的系统响应时间较长，但这并不妨碍系统整体性能的提升，非线性PID控制的整体性能仍优于传统PID控制。

4 总结

本文提出了一种基于非线性PID控制的空气净化系统控制算法，并以室内氧气浓度为控制目标，利用相应时间、调整时间、最大超调量3个控制参数对比分析了本文所提出的非线性PID控制算法与传统PID控制算法的差异。仿真结果表明，本文所提出的空气净化系统控制算法能够保证氧气浓度等参数的控制精度，适合工矿企业等有人值守的工作环境使用。

[1] 段英宏. 空调房间温度预估模糊PID控制器的研究[J]. 系统仿真学报,2008(3)-0620-03.

[2] 梁延东,刘剑. 神经网络在中央空调控制系统中的应用[J]. 白动化与仪器仪表, 2002(4): 25-27.

[3] 邱黎辉,闽沛文,毛义梅. 模糊PID控制在中央空调系统中的应用研究[J]. 计算机测量与控制,2004,12(1):57-59.

[4] 李桂梅,曾喆昭. 一种基于神经网络算法的非线性PID控制器[J]. 中南大学学报(自然科学版),2010(5):1865-1870.

[5] 闫秀英,任庆昌,等. 一种自校正PID控制器设计与仿真研究[J].系统仿真学报, 2006(S2)-0753-04.

[6] 室内空气质量标准[P]，GB/T18883-2002.

[7] 工作场所有害因素职业接触限值(第1部分)：化学有害因素[P]，GBZ2.1-2007.