基于安全字典树的关键词密文模糊搜索方案

张成， 褚莹， 凌力

(复旦大学 通信科学与工程系，上海 200433)

0 引言

近年来，大数据的出现引发了云计算、云存储的蓬勃发展。现在，个人和企业都倾向于将重要的本地数据存储到云端当中以节省开销。加密云端数据让用户减少了本地开销，也保证了数据不会被云端窃取。然而，用户无法直接对密文进行搜索，选择自己需要的数据资源。下载所有密文又费时费力，浪费大量网络开销，为了解决这个问题，提出了可搜索加密的概念。利用安全索引表来对密文进行分类和搜索能够同时满足系统的安全性和高效性。

由于拼写错误会不可避免地出现，传统精确密文搜索方案便具有较大的局限性。2010年，Li等人首先提出了密文关键词模糊搜索的概念[1]。在明文搜索中，利用关键词相似度就可以返回最可能匹配的文档，因此拼写错误的问题比较容易解决，例如输入关键词“hamberger”没有精确匹配文件，但是可以模糊匹配到“hamburger”对应的文件集合。然而，密文搜索时需要搜索的关键词会加密上传到云端，一个简单的拼写错误在加密后就会与正确结果千差万别。因此密文关键词模糊搜索方案可以显著提升系统的可用性以及用户的搜索体验，拥有广阔的应用环境。

文献[1-5]是近年来研究的云端针对加密数据的关键词模糊搜索方案，主要方法是通过编辑距离来度量关键词，制作关键词模糊搜索集合，通过这个集合构建索引表和搜索凭证。利用用户制作好的搜索凭证和存储在云端的索引表进行匹配，将匹配成功的文档集合返回给用户。2012年，文献[2]在文献[1]的基础上提出了一套较为完备的关键词密文模糊搜索方案。和文献[1]的方案相比，Wang等人的方案拥有更好的安全性和可用性。方案使用编辑距离来度量词语之间的相似度，基于通配符来构造空间效率极好的相似词语集合。为了提高这个加密集合的搜索效率，文中使用了字典树(trie)的数据结构来存储关键词加密后的hash值和制作索引表，搜索效率上有了新的突破。

然而，如果用户使用通配符关键词集合，则搜索关键词时需要预先计算关键词所对应的通配符集合，将集合中的每一个元素单独制作一个搜索凭证，再上传到云端进行搜索，增加用户的计算开销以及云端的搜索时间，也增加了泄露相关信息的风险。因此基于通配符的模糊关键词依旧值得改进。

文献[4,5]在构造关键词模糊集合时，不使用编辑距离以及通配符来度量词语相似度，而是使用词语字典内包含的词语和关键词进行对比并制作模糊集合，这种方法可以减小索引表的总数据量，但是依旧不能有效解决单词拼写错误的问题。

针对基于通配符的关键词集合的不足，本文提出了一种新型的模糊关键词搜索方案。本文着重解决的是搜索时不可避免出现的拼写错误，因此本文会基于键盘按键位置来制作模糊关键词集合，虽然相比通配符集合会增加存储的节点数量，但是可以减少用户端的工作，降低用户计算开销，同时由于只制作一个搜索凭证，因此搜索效率也得到了提高，节省了云端的计算开销和带宽资源。在索引表中还混入一些虚假节点，提高云端分析文档和索引表的难度，提高了方案的安全性。

1 系统模型

我们构建一个高阶云端数据服务模型，如图1所示。

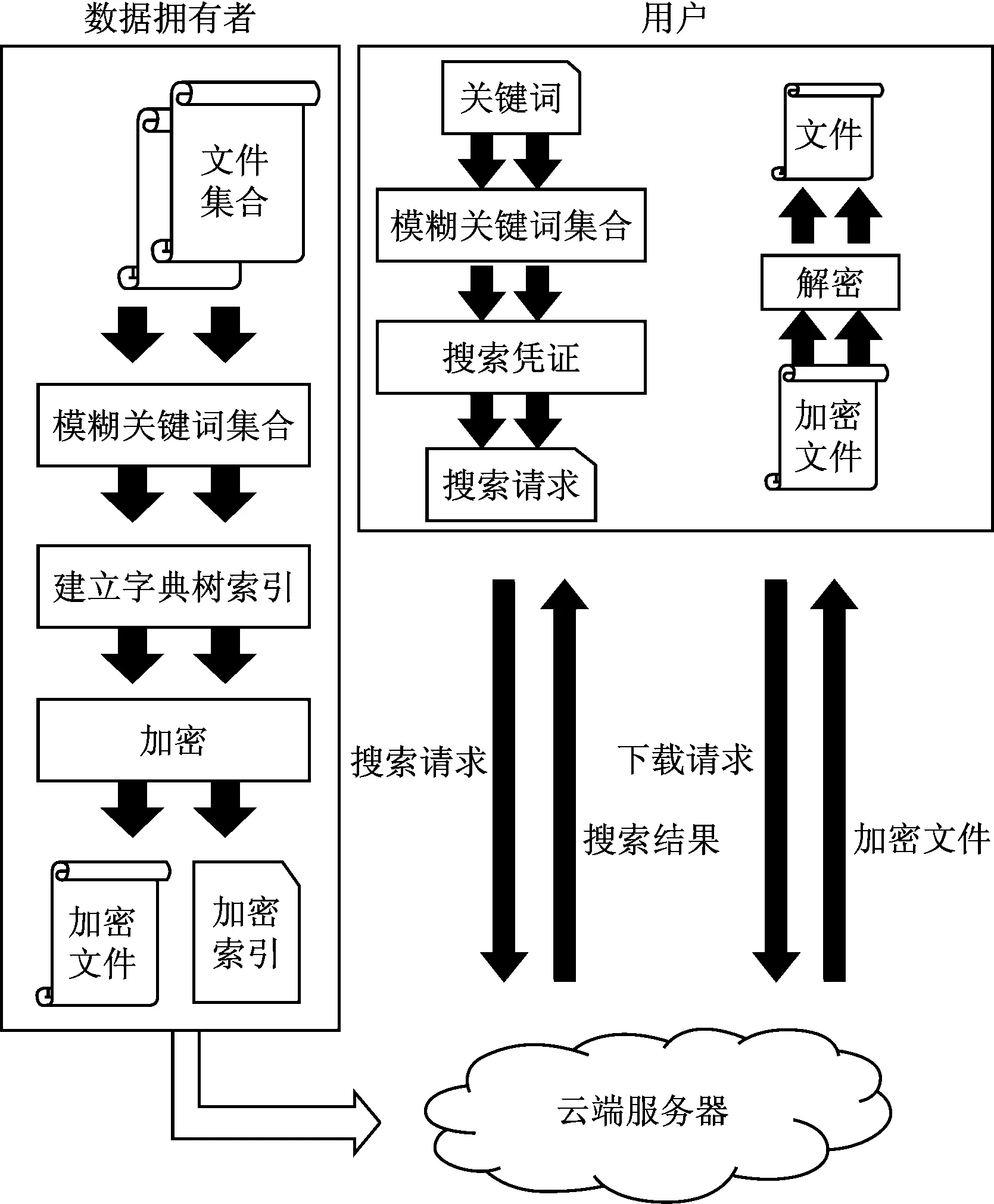
图1 系统模型

模型中存在3个部分：数据拥有者、用户以及云服务器。数据拥有者可能是个人或者企业，加密的数据集合C={F1,F2…Fn}存储在云服务器中。数据集合C当中包含关键词集合W={W1,W2…Wp}。为了保证敏感数据不被盗取，数据拥有者会对数据集合C加密后再上传至云服务器。除此之外，数据拥有者还需要根据关键词集合W构建关键词迷糊集合，根据模糊集合生成搜索凭证Tw，并加入一些混淆凭证，构成索引表Index上传至云端。数据拥有者会将搜索凭证制作秘钥Sk分发给授权用户，用户利用秘钥以及hash等单向函数产生搜索请求凭证。云端在不解密数据的情况下，对数据集合C进行搜索，返回包含指定关键词w的加密文件集合FIDw。搜索方案会根据关键词相似度返回最有可能的文件集合。

在这个模型当中，云服务器只知道数据拥有者上传的密文数据集合C以及索引表Index。云服务器也会诚实地根据用户的搜索请求返回所有符合条件的文件集合，但是会根据数据流分析获取额外信息。

2 关键词模糊搜索方案

2.1 关键词模糊集合的构建

和文献[2～5]相同，本文也使用编辑距离(edit distance)来判定词语之间的相似度。编辑距离，又称为Levenshtein距离，是指将一个字符串转换为另一个字符串所需要的最少编辑次数，许可的编辑操作包括替换字符、插入字符以及删除字符。编辑距离edit(i,j)用于记录str[1…i]和str[1…j]的编辑距离，动态规划公式如下：

1) If i==0&&j==0, edit(i,j) = 0;

2) If i==0&&j>0, edit(i,j) = j;

3) If i>0&&j==0, edit(i,j) = i;

4) If i1&&j1, edit(I,j)==min{edit(i-1,j)+1, edit(i,j-1)+1, edit(i-1,j-1)+f(i,j)}，当第一个字符串的第i个字符不等于第二个字符串的第j个字符时，f(i,j)=1;否则，f(i,j)=0。

本文当中，我们定义Sw,d为某个关键词w对应的相似词语集合，整数d为数据拥有者在制作集合时定义的编辑距离最大值，对于任何w′∈Sw,d，都满足edit(w,w′)≤d。传统模糊关键词集合的构造[2,4-7]都使用基于通配符的模糊集构造方法，对关键词的每个位置的编辑操作都用通配符*表示。例如，对关键词array，构造的基于通配符*编辑距离为1的模糊集合Sarray,1={array，*array，*rray，a*rray，a*ray，arr*ay…arra*，array*}。假设模糊关键词集合的编辑距离是d，那么长度为L的关键词的模糊集合大小为O(Ld)。

基于通配符的方案在明文状态下似乎是一种很合理的方案，但是在对密文搜索时，用户在制作搜索凭证时必须对需要搜索的关键词w计算它的模糊关键词集合Sw,d，这个过程增加了用户的额外开销，也增加了信息泄露的风险。因此本文提出了一种新的基于键盘按键位置的模糊集构造方法。一般的英语单词拼写错误都与键盘相邻按键有关，因此我们可以在构造索引表时只考虑这些元素。例如，按键q的相邻按键为a和w，按键h的相邻按键有y,g,b,n,j等等，经过统计和计算，所有字母可能出现的拼写错误按键总数为92个，因此对于每一个字母按键，将通配符换为相邻字母，平均相邻按键约为3.5个，因此假设模糊关键词集合的编辑距离为d，那么本方案的长度为L的关键词模糊集合大小为

可以看到索引表的大小确实有所增加，但是实际上编辑距离d一般只会选择小于等于2的值，编辑距离d=1时，模糊集合大小约为通配符集合大小的3.5倍；编辑距离d=2时，模糊集合大小约为通配符集合大小的12倍。鉴于基于通配符的索引表一般以MB为计量单位，即使在编辑距离d=2的情况下，我们的方案的索引表数据量依旧是可以接受的。但是在使用本方案后，用户在搜索时不需要制作很多搜索凭证，只需要一条凭证就可以得到需要的结果，节省了用户端和云端两方的计算开销以及时间开销，同时防止了用户制作模糊集合时潜在的信息泄露问题。

2.2 安全字典树索引表结构

为了进一步提高索引表的搜索效率，我们使用一种基于hash值排列的字典树搜索结构来构造索引表，这种多路搜索树用于存储模糊搜索集的所有元素{Sw,d}w∈W。核心思想就是一些元素的hash值会共享一段相同的前缀。定义关键词的hash值αi1αi2…αiτ/λ，树根是一个空集，树的每一条路径αi代表一个字符串，拥有相同前缀的会共用节点。λ为每一个αi包含的比特位，τ为hash值得总比特位，因此总共可以分为τ/λ段。随着树的深入，将从树根到叶子节点的路径上所有字符串拼接在一起，就是叶子节点代表的某个模糊集元素的搜索凭证hash值。

索引字典树通过模糊集合构造而成，计算w的hash值，计算结果平均分为τ/λ段，在字典树的最后一个节点之后，会附加文件索引表，即通往关键词对应的文件集合ID的路径。对每个文件的关键词模糊集合的每一个w作上述操作，直到字典树的完成。结构如图2所示。

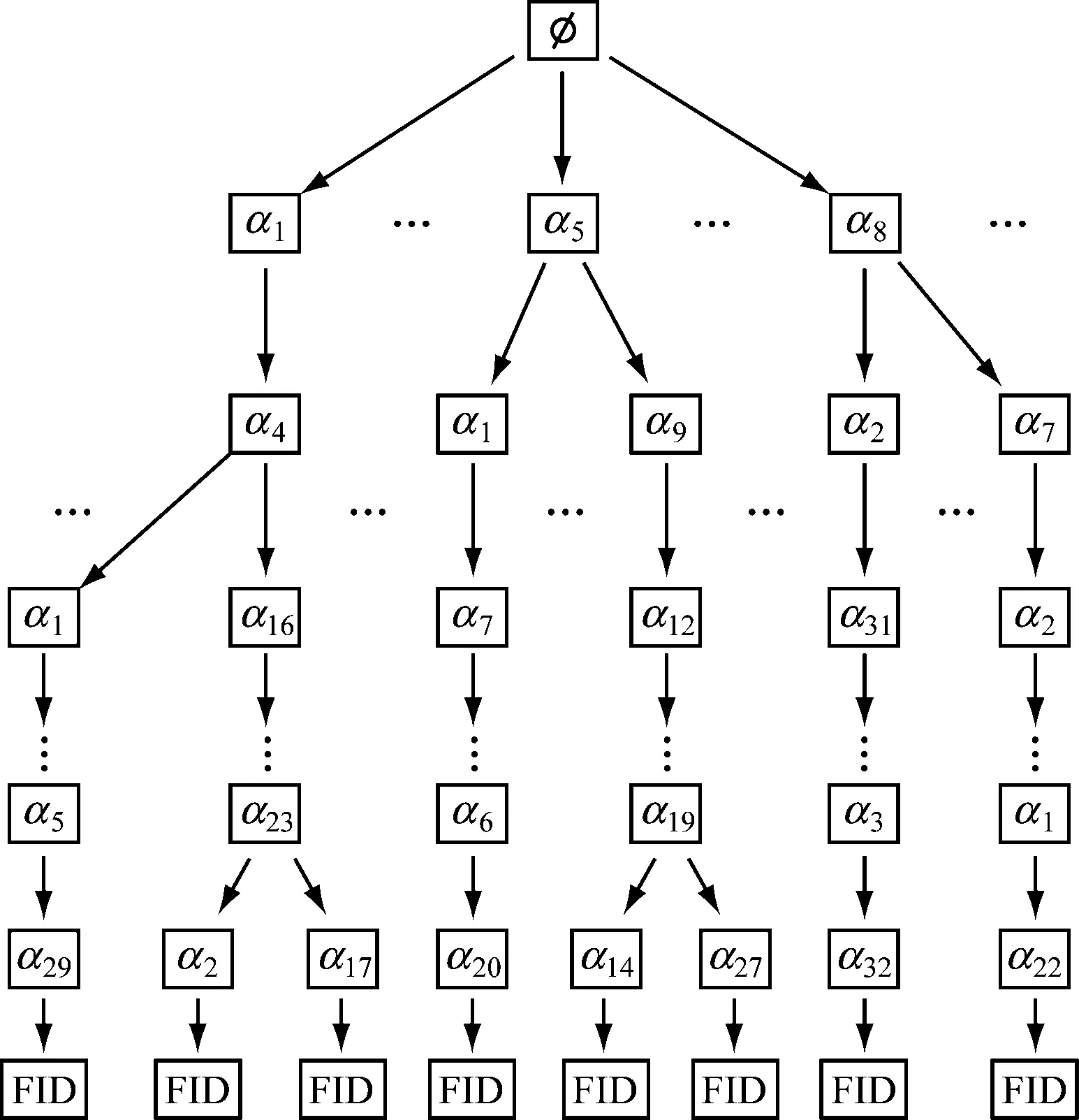
图2 字典索引树结构示意图

由于元素之间的hash值都不同，因此模糊集合的这种分割也是独立不同的。另外，使用这种多路树结构可以完全隐藏关键词w的信息。由于在字典树中不同搜索凭证的路径会共享一些相同的前缀，因此深度搜索可以在常数时间O(τ/λ)完成，和文件总数、关键词总数以及模糊集合节点总数都无关，具有很高的搜索效率。

2.3 索引表建立算法以及搜索算法

预处理阶段：

搜索阶段：

1) 授权用户和数据拥有者安全交互，得到能够获得搜索凭证TWI=f(sk,wi)的秘钥sk。授权用户输入需要查询的关键词w，得到索引凭证Tw。

2) 云端服务器将这些搜索凭证形式上分解为αi1αi2…αiτ/λ的字符串，通过建立好的字典树索引表进行搜索，将对应的文件集合{FIDWI}edit(w,wi)≤d返回给用户。

3) 用户再和数据拥有者进行秘密交互，获得解密秘钥，获得需要的明文文件集合。

由于本文使用的模糊关键词集合无需在制作索引凭证时计算模糊关键词集合，因此搜索时间为O(τ/λ)，即为O(1)的常数时间。而之前文献[2]等人的方案虽然也是用字典树这一数据结构，但是实际搜索之前需要构造{Sw,d}个索引凭证，因此搜索时间需要O(Sw,d)。在编辑距离d=1时约为O(L)，编辑距离d=2时约为O(L2)，时间开销明显降低，减少了很多无意义的搜索。性能对比,如表1所示。

表1 两种方案的性能对比

φ为最大模糊关键词集合的元素个数，|W|为关键词总数。

3 实验性能测试与分析

表1已经在理论上证明，我们的方案能够保护密文的搜索模式和搜索结果，并且增强了搜索效率，达到了常数时间级别。为了证明这一结论，我们使用真实数据集合来验证。我们选择一个包含7000个左右的文件的文本数据集，大小约为400MB。实验配置如下：intel core i7-4790 CPU，7.87G内存。软件环境为：WIN8操作系统以及Java Eclipse编程环境。由于性能的重点在于关键词的数量而不是文件集合的数量，因此我们的实验结果以关键词数量作为横坐标。

设定编辑距离d为1和2时的索引字典树的大小比较。如图3图4所示可以看到基本都是线性增长，d=1时的字典树远远小于d=2的字典树，超过2时效率就会很低，因此方案中不作考虑。制作字典树时使用SHA-1计算hash值，每个搜索凭证的总长度为160 bit。每个子字符串的长度取4 bit，因此树可以分为40层。我们的方案确实在索引大小上高于传统方案，但是大小依旧在MB单位以内，可以接受。由于制作索引只是一次性的，而且可以在线下操作，而且得到了搜索时间性能的提升，因此是可以接受的。

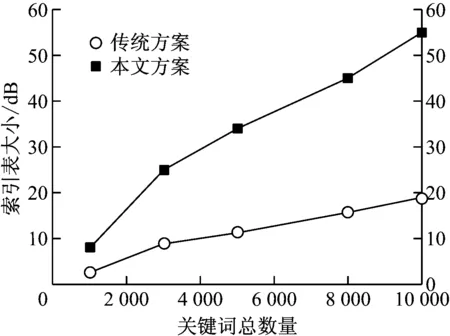
图3 编辑距离为1时的索引大小

图4 编辑距离为2时的索引大小

本文方案和传统方案在搜索时间上的对比。如图5所示。

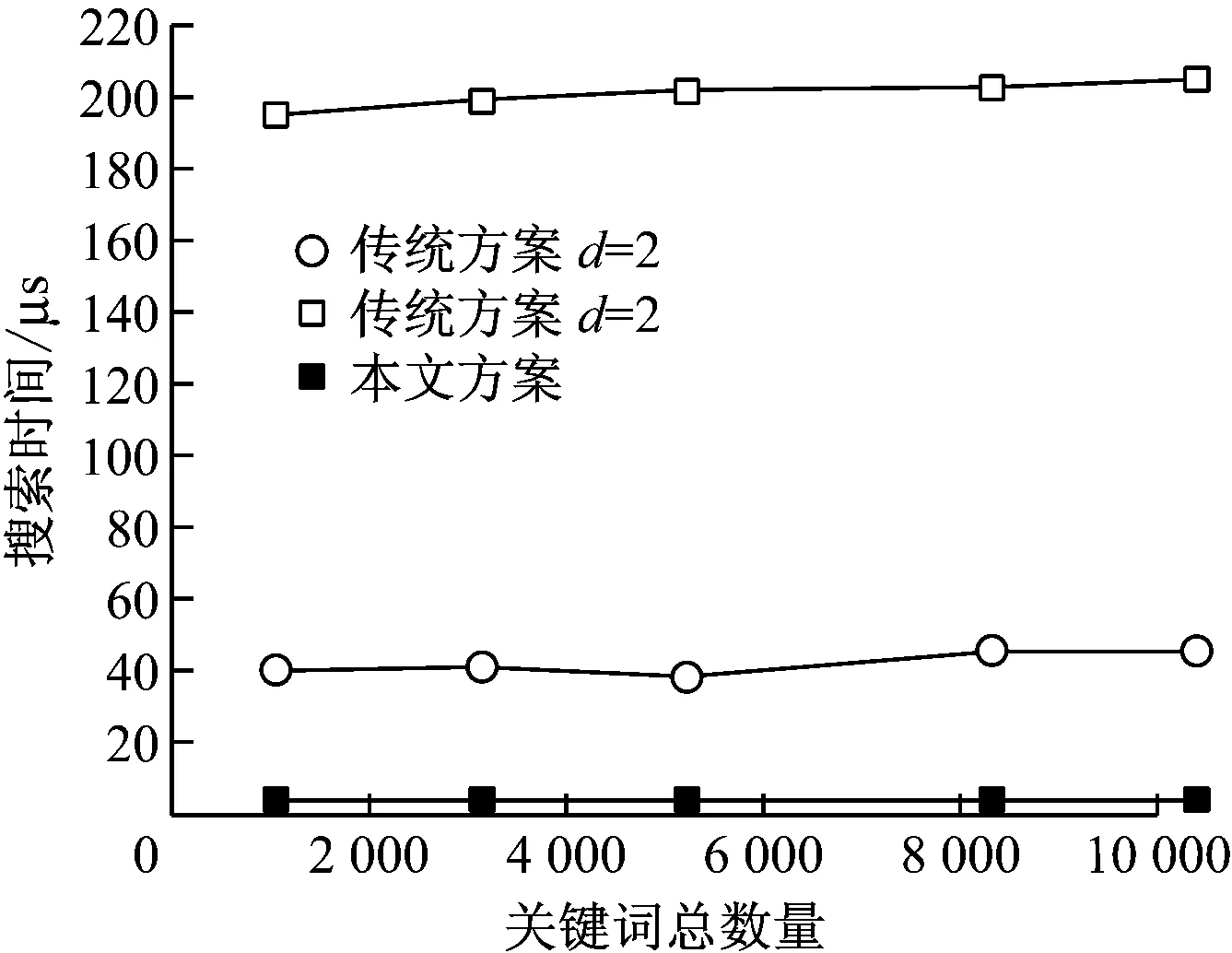
图5 搜索时间对比

可以看到传统方案在编辑距离不同时得到的搜索时间也不相同，因为用户制作的搜索凭证数量不同，因此搜索次数不同。而本文的方案只需要搜索一次，效率上大大提升。

4 总结

针对目前模糊密文搜索中用户制作索引凭证开销大、安全性低的问题，本文提出了一种基于键盘按键位置的模糊关键词集合定义方法。通过分析可能出现的拼写错误，构建了新型的模糊关键词集合以及字典树索引表。尽管提高了字典树索引的大小，但是有效地减少了用户搜索时的计算开销和时间开销，防止用户制作索引凭证的信息泄露，增加了系统的安全性。未来工作中，还可以引入更多有关词语语义的模糊搜索集合，提高搜索效率。

[1] Li J, Wang Q, Wang C, et al. Fuzzy keyword search over encrypted data in cloud computing[J]. Infocom, 2010, 3(9):1-5.

[2] Wang C, Ren K, Yu S, et al. Achieving usable and privacy-assured similarity search over outsourced cloud data[J]. Proceedings - IEEE INFOCOM, 2012, 131(5):451-459.

[3] Kuzu M, Islam M S, Kantarcioglu M. Efficient Similarity Search over Encrypted Data[C]// IEEE, International Conference on Data Engineering. IEEE, 2012:1156-1167.

[4] Liu C, Zhu L, Li L, et al. Fuzzy keyword search on encrypted cloud storage data with small index[J]. 2011:269-273.

[5] Ke T, Zhang W, Ke L I, et al. A Novel Fuzzy Keyword Retrieval Scheme over Encrypted Cloud Data[J]. Wuhan University Journal of Natural Sciences, 2013, 18(5):393-401.

[6] 吴阳, 林柏钢, 杨旸,等. 加密云数据下的关键词模糊搜索方案[J]. 计算机工程与应用, 2015, 51(24):90-96.

[7] 杜军强, 杨波. 云计算中加密数据的模糊关键字搜索方法[J]. 计算机工程与应用, 2015, 51(5):146-152.