带订单选择车辆路径问题的模型与算法

孙刘诚，孙 焰

(同济大学道路与交通工程教育部重点实验室，上海201804)

0 引言

物流是社会活动的经济基础，然而由于物流资源分散、信息封闭、重复配送等，导致物流成本一直居高不下.共同配送作为一种低成本、高效率的协作型配送模式，受到了学者和从业者等各界人士的广泛关注.共同配送包括多种形式，其中很重要的一种形式是通过企业间的信息共享，从而实现运输订单在合作企业间的相互交换和协调，企业车辆互相代为完成订单，提高车辆装载率，减少车辆的交叉重复行驶，不仅可以降低物流成本、提高企业经济效益，还具有营造良好的交通环境、降低碳排放等社会效益.

这种协作型配送模式衍生出了一类新的车辆路径问题，称为带订单选择的车辆路径问题(Vehicle Routing Problem with Request Selection,VRPRS).在此类问题中，运输企业不仅面对由托运人托付的运输订单，同时也可以通过信息平台接收到由合作企业发布的运输订单.运输企业既可以将自身订单委托给合作企业，同时支付一定的委托费；也可以接受其他企业发布的订单，并获得相应的报酬.运输企业需要同时进行订单选择及车辆路径优化使得自己利益最大化.

由于共同配送是近年才发展并兴起的协同物流运作模式中的重要内容，故目前在此背景下的车辆路径问题研究较少.Chu[1]首先提出了在运力不足的情况下可将运输订单外包给其他合作企业的车辆路径问题，并设计了一种启发式算法求解；Bolduc[2]之后加强了前者的求解能力；Côté[3]随后完善了该问题的定义，称该类问题为带公共承运人的车辆路径问题(Vehicle Routing Problem with Private Fleet and Common Carriers,VRPPC)，并开发了更为有效的算法如扰动型元启发式算法和禁忌搜索算法，能求解更大规模的该问题.Liu[4]研究了整车运输下的带订单选择的取送货问题(Pickup and Delivery Problem,PDP)，并考虑了既可以将订单委托给合作企业，也可以接受其他企业的委托.

共同配送环境下的车辆路径问题取得了一定的成果，但除了Liu[4]外，其他研究仅考虑了可将订单外包给合作企业，忽略了还可以选择完成其他企业的发布的订单，并且Liu[4]针对的是整车运输取送货问题，没有考虑更一般意义下的车辆路径问题.因此本文从一家运输企业角度出发，在需要同时进行订单选择及车辆路径优化的条件下，对此类车辆路径问题提出了新的模型和算法，为共同配送系统中的个体行为分析提供了理论基础.

1 基于订单选择的共同配送可行性分析

传统的共同配送概念中，一般是将所有企业的订单信息、车辆信息集中起来进行资源优化.但是实施存在困难，一是谁将占据主导地位难以达成一致，二是企业往往不愿意共享所有商业信息.在此背景下，一种基于订单选择的共同配送模式应运而生，其主要步骤描述如下：

(1)各运输企业将边际收益较低的若干订单发布到共享“订单池”中；

(2)各运输企业根据“订单池”及各自其余订单情况提出订单取舍意向；

(3)联盟决策中心根据各企业订单取舍意向按某种机制重新分配订单，并返回步骤(2)，直至所有订单最终分配完毕；

(4)联盟决策中心根据各企业的贡献程度进行利益分配.

与前面模式不同，该模式下各企业地位平等，不必暴露过多商业信息，具备很强的落地潜力.其中每个步骤都是有待解决的问题，并且需要指出的是，步骤间还存在很强的联系，其交互关系、机制、参数等需要合理制定以尽量满足“激励相容”原则，许多学者就此进行了讨论，如Lai[5]针对整车运输提出了一种基于迭代拍卖的方案达到该目的，Chen[6]则考虑了组合拍卖机制在零担运输协作中的应用.限于篇幅，本文将重点放在步骤(2)，即运输企业的订单选择行为上，剥离出来形成独立的子问题进行研究.

2 模型构建

2.1 问题描述

在上述背景下，本文研究VRPRS的完整描述如下：运输企业面对1组由托运人托付的订单(内部订单，对应的客户称为内部客户)，以及其他合作运输企业发布的订单(外部订单，对应的客户称为外部客户)，可以选择将部分内部订单委托给合作企业，并支付一定的委托费用，同时也可以选择接受部分外部订单获取报酬，确定由本企业完成的1组订单后，合理安排一定数量车辆携带各客户所需的货物从配送中心出发，依次访问客户并最终回到配送中心.问题求解目标是选择由本企业完成的订单，并且优化车辆路径，使得收益最大化.

2.2 模型假设

为了便于研究，该问题有如下前提假设：

(1)外部订单是合作企业发布的边际收益最低的订单(如地理上的离群客户点等)，本企业可自由选择；

(2)委托给合作企业的订单不会被拒绝；

(3)所有货物初始均在一个公共配送中心，运输企业车辆由此装货出发；

(4)货物互相兼容可以混装；

(5)企业拥有的车辆数资源固定，避免运输企业无限接收订单；

(6)考虑到公共客户总需求量可能大于车辆最大容量，允许客户需求可拆分，即1个客户可由多辆车辆服务.

2.3 符号说明

根据图论的理论，该问题可以定义在一个有向图G=(V,A)上，点集V={0}⋃C，点{}0代表公共配送中心，C=CS⋃CA代表客户点的集合，其中CS表示内部客户，CA表示外部客户，弧集A=({0}⋃C)×({0}⋃C).

(1)模型使用参数.

L——合作企业集合({}0代表本企业)；

Q——车辆容量；

cij——从点i到点j的费用，i,j∈V；

e——托运人托付订单的单位收益；

g——完成委托订单的单位收益；

h——委托给外部企业的单位成本；

K——可用车辆数.

(2)模型的决策变量.

xij——从i到j行驶的车辆数，i,j∈V；

qij——点i到点j的货流量，i,j∈V；

2.4 VRPRS模型构建

根据上述符号，可构建VRPRS的混合整数规划模型为

式(1)为目标函数，表示企业获得的总收益最大化，总收益计算公式为：托运人托付的订单的收益+完成外部委托订单的收益—委托给外部企业的成本—车辆可变成本；式(2)保证客户点满足的流量约束；式(3)保证配送中心的流量约束；式(4)表示不会有货物回流到配送中心；式(5)保证满足车辆流约束；式(6)保证使用车辆数不超过最大可用车辆数；式(7)保证车辆容量满足约束；式(8)保证货流量非负；式(9)和式(10)保证部分参数为0-1变量.

2.5 普通CVRP模型构建

为了与运输企业仅完成内部订单的经济效益进行对比，这里另外提出了普通带容量约束的车辆路径问题(Capacitated Vehicle Routing Problem，CVRP)模型.将VRPRS模型中的式(10)替换为

式(11)表示完成托运人托付的所有订单；式(12)表示不接受其他企业的任何委托订单.由式(1)～式(9)，式(11)和式(12)组成的模型即为普通版CVRP模型.

3 算法设计

由于VRP为NP-Hard问题，所以其延伸问题VRPRS同样为NP-Hard问题，精确算法会导致维度爆炸，无法在有效时间内求解，故考虑启发式算法.因遗传算法具有较好的全局寻优能力，在VRP问题上有较好的应用，决定针对本文问题，设计该算法进行求解.

3.1 染色体编码

本文染色体采取十进制编码，将客户序号按一定顺序排列，从而形成一个染色体.这类染色体简洁直观，在旅行商问题(Traveling Salesman Problem,TSP)中应用广泛.但是由于在VRP问题里客户由多辆车辆服务，因此推广到VRP问题时还涉及到解码问题，即将一串十进制染色体编码进行分割，每段编码对应一辆车的访问顺序，从而转化为可行解的结构，可以进一步求得染色体对应的适应度.为解决这一问题，大多数研究里引入了贪婪算法或在染色体中添加编码0代表切割点，但是前者作为一种启发式算法导致难以覆盖到某些解空间，损失了一定的精度；而后者则在染色体交叉时产生了大量不可行解，降低了算法的求解效率.Beasley[7]针对普通VRP问题提出了一种分割算法，算法对客户点的任意组合顺序，巧妙的将分割问题转化为最短路问题，并利用现有的最短路算法在多项式时间内求得其对应的最优分割结果.本文由于车辆数有限制，涉及到各客户的取舍，因此需对这种分割算法进行改进.

基于其思路，设计了一种针对本文问题的染色体编码规则和对应的分割算法，描述如下：

设定染色体为P=(p1p2…pn)，n为客户数，其中前m个基因(p1…pm)为由本企业服务的内部客户和接受委托的外部客户，后n-m个基因(pm+1…pn)为委托给合作企业的内部客户或者不接受委托的外部客户.

对由本企业服务的客户，即前m个基因(p1…pm)，构造一张辅助图G′=(V′,E′)，其中，V′代表点集{0,1,…,m}，E′代表有向边集.对于边(i,j)，其中i,j∈V′，i＜j，若满足容量约束式(13)和式(14)，则边(i,j)的费用如式(15)所示；否则，费用设为无穷大inf.

对于基因段(p1…pm)，其对应的最优分割为在图G′中寻求从0到m的最短路问题，设最短路径长度为sm，那么在该m取值下对应的染色体P=(p1p2…pn)的总收益，即适应度为

对所有的1≤m≤n，求出U(m)的最大值max(U(m))，则该值为染色体P=(p1p2…pn)最终适应度值.最短路算法采取Dijkstra算法，则本文的染色体分割算法时间复杂度为O(n3).

3.2 染色体的选择交叉与变异

本文选择轮盘赌为染色体选择的方式，并每次选择均保留历史最优解以免优秀基因的消失，以概率α选择次序交叉法(Order Crossover,OX)为染色体交叉方法.该方法从父代中随机选取一段路径，并保持另一个父代中城市的相对次序，示例如图1所示.

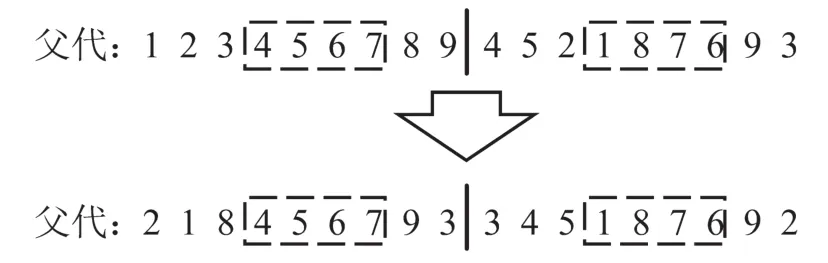
图1 染色体次序交叉示例Fig.1 Example of OX in the chromosome

对染色体以一定的概率β进行变异操作，变异的方法为经典的2-opt算子：将染色体中随机一段基因取逆序放入原位置.

3.3 算法整体框架

本文遗传算法的框架如图2所示.

4 算例分析

本节将对算法进行一系列数值实验.首先在经典的CVRP数据集上对算法的有效性进行了分析，而针对本文提出的问题，由于目前不存在该问题的标准算例，因此构造产生各种规模算例进行测试，并进行结果分析.算法由Matlab编程实现，并在Intel Core i5-4590 CPU@3.30GHz处理器，8GB内存计算机上进行计算.

4.1 算法有效性分析

为验证本文算法的有效性，与已知最优解的CVRP部分算例[8]进行了对比，解保留到个位数，结果如表1所示.其中，IGA表示本文算法的解，BN表示已知最优解，Gap表示与已知最优解的差距(%)，Time表示求解时间(s).

与已知最优解的对比表明，本文算法能在可接受时间内较好地逼近最优解，并且在部分中小规模算例中能达到最优解，说明了本文算法的有效性.

4.2 算例构造

公共配送中心的坐标为(0,0)，客户点均在[1 0 ,90]×[1 0 ,90]的平面内随机生成，客户对各原指定运输企业的货物配送需求为0或者[5,15]之间的随机数，客户中存在同时对多个运输企业均有货物配送需求的，称为共同客户，共同客户占比设为10%，内部客户占比设为60%，并有2个合作企业.费用cij设为点i到点j的欧氏距离.控制最大车辆数为，即刚好满足原运输需求的最小车辆数，使得企业更倾向于进行合理的订单选择而不是简单通过完成更多订单增加经济效益.其他参数设定如表2所示.客户数100以下的称为小规模算例，100及以上的称为大规模算例.算例命名由所有客户数和本企业车辆数构成，如“n100-k8”表示100个客户，8辆自有车辆的算例.

图2 算法框架Fig.2 Algorithm framework

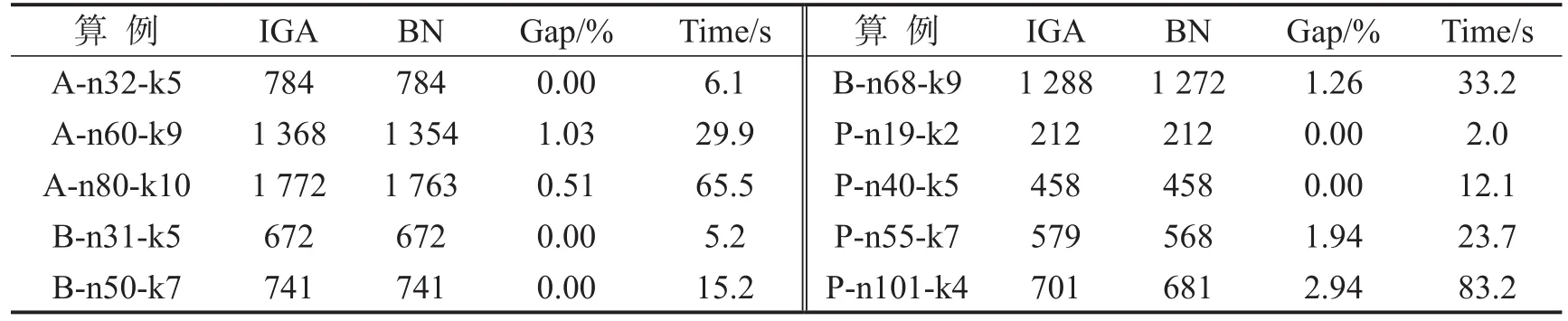
表1 本文解对比已知最优解Table 1 IGA vs.Best known

表2 算例参数设置Table 2 Instance parameter settings

4.3 结果分析

本文遗传算法中设定交叉概率为0.75，变异概率为0.05，种群规模为60，初始种群随机生成，终止条件为经过100次迭代历史最优解仍没有更新.数值实验结果如表3所示.其中 B-CVRP，B-VRPRS，B-Gap分别表示普通配送的收益，带订单选择的配送收益，以及收益提升的百分比(%)；C-CVRP，C-VRPRS，C-Gap分别表示普通配送的车辆行驶距离，带订单选择配送的车辆行驶距离，以及行驶距离增加的百分比(%).结果表明，企业的收益平均有8.22%的提升，并且车辆的行驶路径反而有所减少，平均减幅达到18.41%.可以看出，在共同配送模式下，通过订单的双向委托，运输企业的个体选择行为不仅有利于企业经济效益的提高，并且对于减少汽车配送行驶距离，从而帮助提升交通环境，降低碳排放等有着积极的作用.

表3 数值实验结果Table 3 Results of the numerical experiments

将n20-k2算例的优化结果展示如图3所示(订单选择前后的车辆路径).可以观察到，为了尽可能获得更大利益，运输企业将若干个离群内部客户点委托给了合作企业，选择了其他企业发布的更加顺路的外部客户点，使得其服务客户在地理上更加集中，从而使得车辆行驶距离减少，降低了运输成本.

图3 订单选择前后车辆路径Fig.3 Vehicle routing before and after request selection

5 结论

本文在共同配送环境下，基于企业间可以双向委托订单的策略，提出了一种新的带订单选择的车辆路径问题，以最大化企业经济效益为目标建立了混合整数规划模型.针对此NP-Hard问题，设计了遗传算法，并提出了针对该问题染色体编码的解码的一种多项式时间最优分割算法.通过数值实验，发现通过订单交换和协调，一家运输企业的个体选择行为，不仅能够提高企业的利润，并能够一定程度上减少车辆的行驶距离，实现企业经济效益和社会效益的双赢.本文的研究是以一家运输企业为主体进行的，重点在于分析联盟中的个体订单选择行为.未来的研究主体将转移到多家运输企业的共同配送联盟，考虑合作企业间委托任务价格的敏感性等，充分分析委托代理双方的互动关系，通过制定合理的委托策略结合个体行为反应，以达到共同配送联盟各方合作博弈的目的.

参考文献：

[1]CHU C W.A heuristic algorithm for the truckload and less-than-truckload problem[J].European Journal of Operational Research,2005,165(3):657-667.

[2]BOLDUC M C,RENAUD J,BOCTOR F,et al.A perturbation metaheuristic for the vehicle routing problem with private fleet and common carriers[J].Journal of the Operational Research Society,2008,59(6):776-787.

[3]CÔTÉ J F,POTVIN J Y.A tabu search heuristic for the vehicle routing problem with private fleet and common carrier[J].European Journal of Operational Research,2009,198(2):464-469.

[4]LIU R,JIANG Z,LIU X,et al.Task selection and routing problems in collaborative truckload transportation[J].Transportation Research Part E Logistics&Transportation Review,2010,46(6):1071-1085.

[5]LAI M,CAI X,HU Q.An iterative auction for carrier collaboration in truckload pickup and delivery[J].Transportation Research Part E Logistics &Transportation Review,2017(107):60-80.

[6]CHEN H.Combinatorial clock-proxy exchange for carrier collaboration in less than truck load transportation[J].Transportation Research Part E Logistics&Transportation Review,2016(91):152-172.

[7]BEASLEY J E.Route first—Cluster second methods for vehicle routing[J].Omega,1983,11(4):403-408.

[8]AUGERAT P,BELENGUER J,BENAVENT E,et al.Computational results with a branch and cut code for the capacitated vehicle routing problem[J].Rapport De Recherche-IMAG,1995:495.