共享自行车系统动态调度时间域的获取方法

刘冬旭，董红召

(1.浙江工业大学智能交通系统联合研究所，杭州310014；2.浙江广播电视大学信息学院杭州310012)

0 引言

共享自行车系统(Bicycle Sharing System，BSS)目前分为锁桩式BSS(公共自行车)和无锁桩式BSS(共享单车)，锁桩式BSS通过自助租赁点提供租还服务，共享单车通过电子围栏等方式来解决无序停放问题.然而两者都有停放自行车容量的限制，都面临着交通出行需求的时空分布不均衡问题，租还车难将成为2种BSS共同的突出现象，因而，BSS服务点平衡调度技术成为研究的焦点.调度何时开始、多长时间完成，影响着BSS的调度效率、成本及服务等级，因此，研究BSS服务点调度的时机选择非常重要.

BSS数据分析的研究较多，如滕磊等[1]运用统计分析、聚类分析等方法研究了城市公共自行车系统的借还车频次、用车时长、站点和锁桩设置等问题；国际交通地理期刊用专辑分析了共享式自行车社会、经济、文化、气候地理等特征[2]；但以上文献都缺少对BSS流动特性规律的研究.

针对公共自行车的调度，董红召等提出了公共自行车系统调度的滚动时域调度算法[3]，并进行了调度区域聚类划分[4]，基于大样本历史数据对公共自行车服务点自然租赁需求进行了估算及验证[5].林燕平等[6]提出了基于网络图的某站点自行车的需求量预测模型.J.Schuijbroek等[7]考虑服务级别和调度成本，提出了先聚类后路由的公共自行车分配方案.但是BSS调度时机的获取，还停留在经验阶段，缺少理论计算方法.

为了解决这些问题，可以通过对BSS运行历史数据的分析，获取合理的调度时机，为此，提出了一种BSS自流动模型及BSS动态调度时间域的获取方法.调度时间域是BSS服务点持续处于需要调入或调出自行车状态的时间区间，旨在帮助管理者选择调度的最佳时机，既要避免无法租还车，也要尽量减少调度频次.最后，以杭州锁桩式BSS调度为例对算法进行实验验证.

1 BSS自流动模型的提出

BSS因租用者使用而发生的位置移动，称为“自流动”.自流动特性反映了自行车用户的出行规律，也是BSS管理者选择什么时间、哪些服务点需要进行调度的重要决策依据.为了分析共享自行车流动性特征，这里提出了用服务点自行车周转率、租还量差异、车容比、空/满位等描述不同时间、空间尺度上服务点状态变化的BSS自流动模型，并以此计算出动态调度介入的时间域.BSS自流动模型及算法的框架流程结构如图1所示.

图1 BSS自流动模型及动态调度时间域获取方法Fig.1 Self-moving model and scheduling time ranges algorithm of BSS

1.1 BSS自流动模型的流动性分析

(1)服务点自行车租还量.

服务点i在某时间段τ的自行车租还量Zi(τ)为该时段还车数量和借车数量的总和，其计算方法为

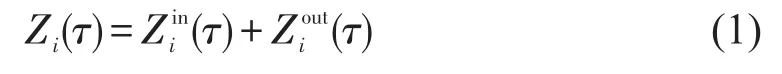
(2)服务点自行车周转率.

服务点i在某时间段τ的自行车周转率ri(τ)包括借车周转率和还车周转率，而借/还车周转率分别定义为服务点i在时间段τ的自行车租/还量与该服务点的停车能力Ei(锁桩数或者电子围栏设计容量)的比值，计算方法为

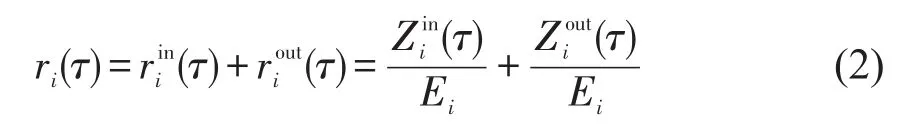
1.2 BSS自流动模型的时变分析

(1)服务点租还量差异.

服务点的自行车租借量和归还量随着时间而变化，往往因不平衡而导致潮汐现象，因此引入租还量差异参数Li(τ)来表示服务点i在时间段τ内的自行车租还量差异，其计算方法为

(2)服务点车容比(停车集中指数).

服务点的停车集中指数在公共自行车领域通常被称为车容比，这里定义为某服务点i在时刻t时保有的自行车数量qi(t)与该服务点停车能力Ei的比值，取值范围为[0，1]，这是表征服务点时变特性的重要概念.设t0为初始时间，qi(t0)为服务点i的初始自行车保有量，服务点i在t时刻的车容比Hi(t)将受到之前租还量差异Li(t-t0)的直接影响，计算公式为

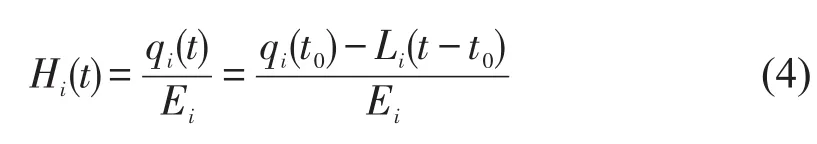
(3)服务点空/满位车容比阈值.

服务点的租还量差异和车容比变化可能会导致服务点进入空/满位状态，当某时间区间内Li(τ)＞0，Hi(t)将持续变小甚至接近0，服务点进入空位状态，借车困难；而当Li(τ)＜ 0时，Hi(t)持续变大直至接近1，服务点进入满位状态，还车困难.令表示车容比满位阈值，表示车容比空位阈值，车容比阈值及服务点i状态的判断规则如下：

2 基于BSS自流动模型的动态调度时间域获取算法

根据BSS自流动模型可以计算出服务点处于空位和满位的时间段，即介入调度的动态时间域.理想的服务点车容比阈值的取值范围是[0,1]，在实际运营过程中，在服务点只剩少量自行车可借出或少量空锁桩可还车时，就定义为空/满状态，即车容比阈值范围变小.同时，周转率高的服务点往往对居民出行和整个BSS的影响程度比较高，因此，对应的调度要提前安排，即车容比阈值范围变小.在统筹考虑调度响应速度和服务点自行车周转率基础上，设计空/满位的车容比阈值算法为

式中：τ为时间段，可以分别取某一工作日及节假日的一天.ri(τ)是服务点i的自行车周转率，ri(τ)值越大，说明该服务点在BSS中越重要，调度应介入越早.rmax(τ)是所有服务点周转率最大值，rmin(τ)是最小值，是周转率ri(τ)的归一化数值，取值范围[0，1].ε是周转率的本地化系数，表示服务点自行车周转率对车容比阈值的影响程度，如ε值越大，则不同服务点的自行车周转率对其车容比阈值的影响越大.[ωmin,ωmax]是一个与调度响应速度关联的空满位判断基准阈值，如果不考虑调度延迟，即服务点一旦发出调度需求，调度车就可立即到达现场，则服务点可以等到其状态变成完全空(没有自行车)或满(没有空锁桩)时，再发出调度请求，此时车容比为0和1，因此，基准阈值也取[0,1].但实际上调度车到达现场有延迟，所以基准阈值范围应小于[0,1]，BSS响应速度越快，即调度车到达现场所需时间越短，则基准阈值取值越接近[0,1].

服务点i的期望车容比为阈值的中间值，在平衡而稳定的周转率情况下，，即服务点自行车保有量为设计停车能力的1/2.然而，BBS在实际运行过程中，服务点的周转率常常并非平衡稳定状态，期望车容比也会受到下一时段租还量差异Li(τ)的影响.如果下一时段租借量大于归还量，即Li(τ)＞0，期望车容比应大于0.5，车容比阈值也右移；反之，则期望车容比应小于0.5，阈值左移.令Tt表示t时刻开始、时长为T的时段，每个时段的期望车容比及车容比阈值算法进一步改进为

式中：Tt+T表示t+T时刻开始、时长为T的时段，即Tt的下一时段；Li(Tt+T)是服务点i在Tt下一时段的租还量差异，取值范围是[-1,1]；μ是租还量差异的本地化系数，表示服务点下一时段的租还差异对其车容比阈值的影响程度，如μ值越大，则服务点下一时段的租还差异对车容比阈值的影响越大.式(7)～式(9)中，和阈值将根据Tt下一时段租还量差异Li(Tt+T)的变化而不同，具体分3种情况：

(1)Li(Tt+T)=0，则式(8)和式(9)等同于式(5)和式(6)，

(2)Li(Tt+T)＞0，则阈值范围右移，

(3)Li(Tt+T)＜0，则阈值范围左移，

计算出服务点车容比阈值后，通过分析服务点车容比沿时间轴的动态演变规律和分布特性，可以确定各类服务点在自流动影响下的失衡程度和需要介入调度的动态时间域.

服务点需调入自行车的正调度时间域用[WIlow,WIupp]表示，这里WIlow和WIupp分别表示时间域的开始时间和结束时间，设有n个正调度动态时间域：k=1,2,…,n，计算方法如式(10)所示.与此相同，设有m个负调度时间域需调出自行车，用k=1,2,…,m，表示，则计算方法如式(11)所示.

式中：σ表示车容比取值的时间间隔.

3 BSS动态调度时间域获取方法的实践应用

基于杭州市下沙地区锁桩式BSS的2016年历史运行数据，对提出的BSS自流动模型及调度时间域算法进行实验验证.在分析几种不同类型服务点周转率的基础上，以居民区类型编号3758服务点的11月份工作日为例，对调度时间域进行计算和分析.

3.1 服务点周转率分析

表1给出了不同类型服务点工作日和节假日的周转率.居民区、学校及大型公交中转站的服务点周转率工作日略大于节假日；而景区和商业区的服务点周转率在节假日远超工作日，节假日期间需要加大对景区和商业区服务点的调度.

表1 不同类型服务点工作日和节假日自行车周转率比较Table 1 Bicycle turnover rates at different types of stations on working days and holidays

3.2 服务点时变分析

以编号3758服务点为例，比较工作日与节假日的自行车租借量与归还量，可得出各时段的租还量差异，如图2所示，工作日早高峰租借量很大，晚高峰归还量很大，容易出现空/满位状态.

3.3 动态调度时间域计算实例和调度方案结果分析

调度响应时间是BSS服务质量等级的重要指标，实验采用表2所示对应关系.表2中调度响应时间[θmin,θmax]是服务点发出调度需求到获得调度服务的理想时间范围.当服务点空/满位持续时间大于最小响应时间时，对该服务点进行调度.

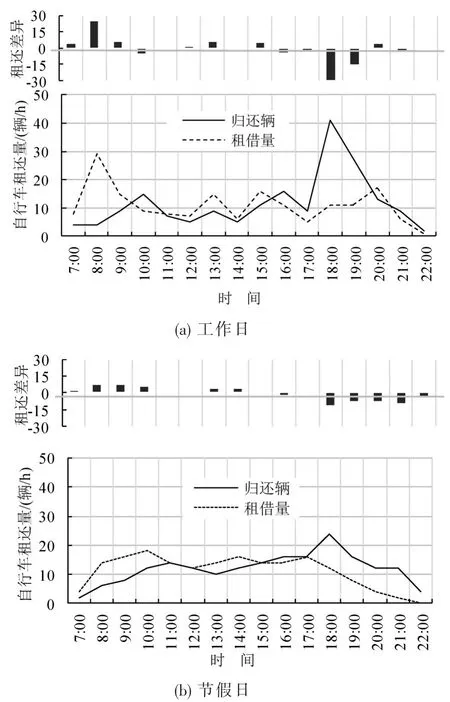
图2 编号3758服务点工作日和节假日租还量时变曲线及差异Fig.2 Dynamic differences between rentals and returns at No.3758 station on working days and holidays

用编号3758服务点工作日的运行数据进行计算.根据BSS运行机构本地化实践经验、结合服务点的周转率等数据分析，用户的调度策略可以通过服务质量等级、空满位判断基准阈值、自流动率本地化系数的综合作用来实现.实验中设定基准阈值取[0.1,0.9]，本地化系数ε和μ取值0.1(限于篇幅，3个取值的详细图表分析可向作者索取).由式(7)计算可得工作日各时段的期望车容比，由式(8)和式(9)计算各时段触发调度的空/满位车容比动态阈值，结果如表3所示.

表2 BSS服务等级与调度响应时间Table 2 The response time for different service level of BSS (min)

采用表3中动态阈值，根据式(10)和式(11)可得编号3758服务点的动态调度时间域如表4所示.同时，如果采用其基准阈值作为固定阈值，即[0.1,0.9]，则也可以获取相应的调度时间域.

从表4可以看出，采用固定基准阈值得出的调度时间域持续时间更长，采用动态阈值则呈现为短时的动态时间域，如早高峰时的正调度为[8:10,8:20]、[8:30,9:00]、[9:20,9:30]，而在固定阈值情况下为[8:10,9:35]，几乎持续整个早高峰时段，而晚高峰负调度时间域也发生同样情况.另外，采用固定阈值得出的正调度时间域[16:05,16:35]在动态阈值情况下没有出现，因为动态阈值的计算考虑了下一时段的租还量需求，因此，即使该时段的自行车保有量非常少，但因晚高峰有大量还车，该时段实际并不需要调度，即动态阈值可减少一些不必要的调度.

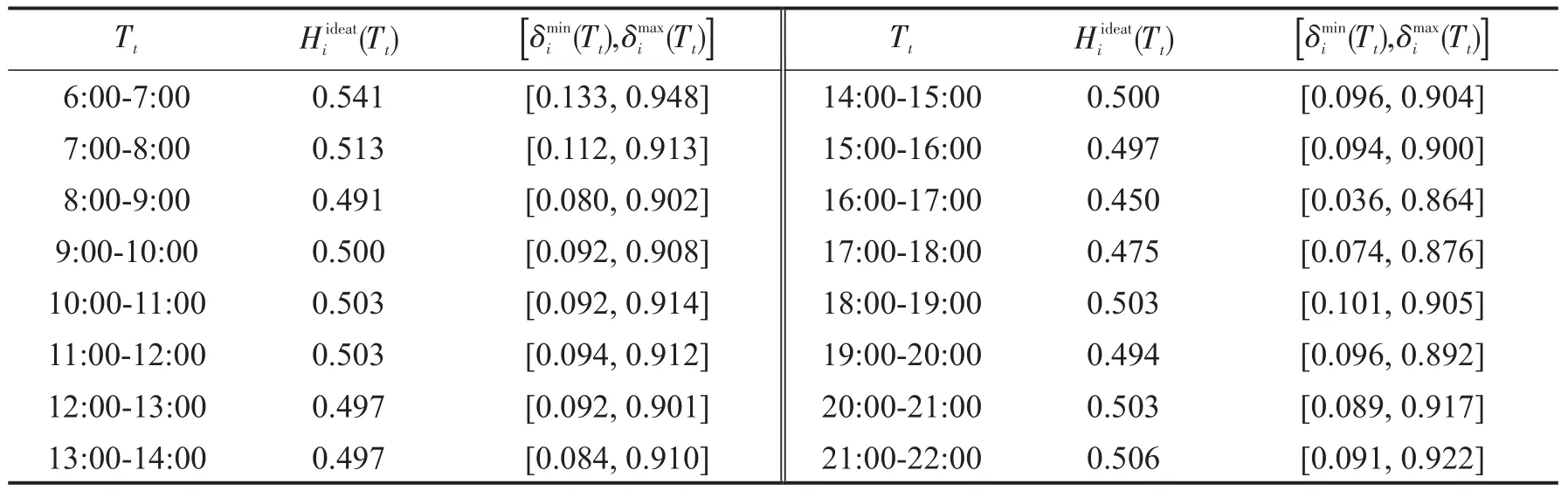
表3 编号3758服务点工作日的期望车容比和车容比阈值Table 3 Ideal value and threshold range of occupancy-capacity ratio at No.3758 station on working days

表4 不同车容比阈值下编号3758服务点工作日的调度时间域Table 4 Scheduling time ranges with dynamic or fixed threshold at No.3758 station on working days

根据表2，BSS的2级服务最小调度响应时间θmin是20 min，比较表4中调度时间域与θmin，只有大于θmin的调度时间域需要实施调度.因此可以得到2种方案所需要的调度次数，表4中“*”标记表示需要实施BSS调度的时间域，动态阈值方法的正调度最少需要3次，负调度需要2次；采用固定基准阈值方法则正调度最少需要5次(因为时间域[8:10，9:35]过长，可能需要调度2次，即正调度需要6次)，负调度需要3次.

显然，采用车容比动态阈值计算方法指导BSS的调度决策，比固定阈值更加精准有效，充分利用了BSS，自行车租借归还的流动时变性，服务点能够在某段时间内达到自平衡，从而帮助BSS管理人员确定调度介入的时机，在满足BSS运行的调度服务等级情况下，可以合理减少调度频次，从而提高了工作效率、降低服务成本.

4 结论

BSS自流动特性对确定合理的调度时间域具有决定性的影响.因此，提出了用自流动模型来描述BSS的流动特性，综合考虑了调度基准阈值、BSS服务点的自行车周转率及租还量差异等特性，给出了自行车调入/调出服务点的正/负调度时间域算法.以杭州市锁桩式BSS作为研究范例，分析比较了编号3758服务点空/满位判断车容比动态阈值与经验固定阈值情况下的动态调度时间域效果.实践证明所提出的BSS动态调度时间域获取方法能够减少调度频次、降低服务成本、并提高调度时机的精准度.

尽管实验以锁桩式BSS为案例，电子围栏式共享单车(无锁桩BSS)也同样适用该方法.共享单车具有海量出行数据，采用动态调度时间域获取方法，可以帮助管理人员选定共享单车的调度时机，从而优化调度成本和工作效率.

参考文献:

[1]滕磊,洪铃,潘婷婷,等.基于多元统计法公共自行车服务系统的研究[J].山西师范大学学报(自然科学版),2016,30(1):40-43.[TENG L,HONG L,PAN T T,et al.The research public bicycle service system by diverse statistics method[J].Journal of Shanxi Normal University(Natural Science Edition),2016,30(1):40-43.]

[2]CORCORAN J,LI T.Spatial analytical approaches in public bicycle sharing programs[J].Journal of Transport Geography,2014(41):268-271.

[3]董红召,赵敬洋,郭海锋.公共慢行系统的动态调度建模与滚动时域调度算法研究的调度[J].公路工程,2009,34(6):68-75.[DONG H Z,ZHAO J Y,GUO H F.Research on the dynamic model and rolling horizon scheduling algorithm for public-use bicycle vehicle scheduling problem[J].Highway Engineering,2009,34(6):68-75.]

[4]董红召,史彩霞,陈宁,等.基于关联规则的公共自行车调度区域聚类划分[J].科技通报,2013,29(9):209-216.[DONG H Z,SHI C X,CHEN N,et al.Clustering division of public bicycle scheduling regional based on association rules[J].Bulletin of Science and Technology，2013,29(9):209-216.]

[5]董红召,吴满金,刘冬旭,等.城市公共自行车系统自然租赁需求的估算方法[J].浙江大学学报(工学版),2016,50(2):265-270.[DONG H Z,WU M J,LIU D X,et al.Estimation method of natural demand of urban public bicycle system[J].Journal of Zhejiang University(Engineering Science),2016,50(2):265-270.]

[6]林燕平,窦万峰.基于网络模型的城市公共自行车需求量预测研究[J].计算机应用研究,2017,34(9):2692-2695.[LIN Y P,DOU W F.Research on demand prediction of urban bicycle sharing based on network model[J].Application Research of Computers,2017,34(9):2692-2695.]

[7]SCHUIJBROEK J,HAMPSHIRE R C,VANHOEVE W J.Inventory rebalancing and vehicle routing in bike sharing systems[J].European Journal of Operational Research,2017,257(3):992-1004.