有关智能化城市增长模型研究
文/程娅萍 山东科技大学 山东泰安 271000
1、任务一模型的建立与求解
对于任务1,在基本假设条件下,针对影响城市智能化可持续发展的指标,建立了衡量城市智能化增长成功率的三大指标体系,包括城市的人口统计,增长需求和地理条件。
城市化率是城市化的度量指标,一般采用人口统计学指标,即城镇人口占总人口的比重。增长需求体系的建立由土地利用率、国民生产总值以及基础设施利用率组成。地理条件相关指标主要包括土地总面积、总耕地面积、园林地、草滩地、城乡村镇、厂房以及交通用地等面积。
2、任务二模型的建立与求解
对于任务2,利用层次分析法以及模糊评价法进行了建模,首先根据题设条件,根据任务一模型各指标之间的重要关系,利用Matlab计算出各指标的权重值;其次,计算出评判影响城市智能化增长成功程度的总指标参数,根据设立的评价机制进行等级评价,且以金昌市为例,利用软件SPSS进行线性回归分析,验证出模型的可靠性;最后,分析金昌和桑托斯当前城市计划的成功程度。
经过上述一系列计算得出的S值,并进行评级,表示城市智能化可持续发展的合理性。其中,5等为最优,说明各个指标体系搭配完整,人口城市化合理,土地利用率高,国民生产总值满足增长需求,城市地理位置优越;反之,1等为最差情况;从5等到1等其成功依次递减。
3、任务三模型的建立与求解
对于任务3,建立了衡量城市智能化增长成功率的预测模型。通过预测未来20年金昌和桑托斯的城市智能化增长成功指数,结合任务2模型当前计划成功程度指数,得出当前计划是不可行的,且根据城市的地理位置、预期增长率和经济机会制定了新的智能化城市发展计划,并评定了新计划的成功率。
评价模型的发展是有极限的。对于城市智能化增长的评价,在其发展的初期是呈指数曲线变化的,但随着相关政策实施等因素的影响,预测模型应用修正指数曲线:
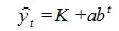
结合计算结果可知:根据任务2 模型的评价标准,金昌城市智能化可持续发展程度逐步上升,但是发展趋势较慢,20年间仅提升了10个指数;桑托斯在城市发展初期呈逐步上升趋势,到2028年以后,城市发展趋势明显放缓;因此,需要为金昌和桑托斯设计新的智能化发展计划。
4、任务四模型的建立与求解
对于任务4,根据任务3模型新计划中的各项计划间的重要关系,利用Matlab进行了权重计算,将各项计划按照最具潜力到最不具潜力进行了排名,并提出各项新计划潜力的排名需要因地制宜。
有关智能化增长计划中的每项计划的新排名。根据制定的新计划中各项计划的权重关系,利用Matlab计算出权重值,根据权重值的大小,对每项计划从最具备潜力到最不具备潜力进行排序。再进行新排名在所选城市中的应用分析(对比各项计划和城市排名的关系)。 因为地理位置差异和经济发展的制衡,该项计划需因地制宜,重新对金昌和桑托斯进行可持续发展新计划排序。
5、任务五模型的建立与求解
对于任务5,根据局部均衡理论,首先构建数学模型,利用Eviews Ver6.0软件估计系统中的三阶段最小二乘法(3SLS)对模型进行参数估计;第二步,设置两个模拟情景以计算研究假说中的外生变量(城市人口)受到冲击时对智能化城市可持续发展成功率的影响;最后,根据模型设计了三种支持方式。
根据局部均衡理论,新计划下,智能化城市可持续发展成功程度综合评判指数计算模型的建立主要基于城镇人口、GDP和土地利用率。根据统计数据,结合Eviews Ver6.0软件估计系统中的三阶段最小二乘法(3SLS)对模型的参数估计,得出智能化可持续发展模型。结合现实中智能化城市可持续发展计划在2006-2015年的相关数据,对模型的单方程进行拟合度检验。检验的指标主要有平均绝对误差、平均相对误差、均方根误差、不等系数。
6、模型优缺点分析
6.1 优点
该模型能够基本解决所提出的所有问题,为衡量一个城市智能化增长成功率提供了借鉴,任务2模型制定的评价标准是与实际情况相符,任务3模型提出的未来几十年城市可持续化增长的新计划能够切实的解决实际问题,并且在任务四模型提出了各项新计划重要性因地制宜的建议,任务5 的均衡模型提出了支撑2050年城市人口增加50%的三种支持方式。
6.2 缺点
因文章篇幅和本团队对问题相关领域认识的限制,5个任务的模型所考虑的因素都不够全面,桑托斯和金昌的能源和资源、以及人为干预等因素都未能考虑进模型,但是,本模型得出的结论基本反映了智能化城市发展的现状和趋势,能够满足解题需要。

