基于航迹质量分析的加权平均融合算法

李素

（四川大学计算机学院，成都，610065）

0 引言

融合估计系统的典型结构分集中式、分布式与混合式三种[1]。其中，分布式融合结构能够以较低的费用得到较好的可靠性和可用性。如图1所示，在分布式多传感器航迹融合系统中[2]，各传感器周期性地将传感器量测发送至跟踪器，跟踪器进行目标跟踪处理得到局部航迹（传感器航迹），然后，将跟踪输出的局部航迹传送至融合中心进行融合处理。航迹融合包括航迹关联和航迹状态估计融合两步。其中，在航迹关联过程中，系统将来自各传感器的局部航迹进行两两关联；而在航迹状态估计过程中，融合中心通过相应的航迹融合算法将那些经过航迹关联后判定为来自同一目标的局部航迹进行融合，形成系统航迹。

一直以来，航迹融合算法都是分布式多传感器融合系统中的一个关键技术[3]。现有的航迹融合算法有加权平均融合方法、简单融合方法、动态权值融合方法等。

加权平均融合是一种有效处理多源传感器数据问题的经典方法，传统的加权平均融合将每一路测量信息完全平均的加权，但并没有考虑传感器因自身差异而导致测量误差相差较大的问题。本文算法将系统航迹与局部航迹的欧氏距离以及其状态向量在1范数下的距离之和作为航迹质量测量度，并进行航迹质量分析，同时剔除航迹质量较差的局部航迹，再根据航迹质量确定各局部航迹的加权因子，最后用加权平均方法进行航迹状态估计，避免了航迹融合效果受传感器自身测量误差的影响，同时也解决了当传感器数量增加到一定数目时融合精度并没有持续提高甚至下降的问题。

图1 分布式多传感器融合系统结构框图

1 航迹融合

一般情况下，当传感器的测量误差越小，其局部航迹的航迹质量越好，当传感器的测量越大时，其局部航迹的航迹质量越差。统计方差分析法将局部航迹在各个时刻的平均方差作为评价航迹质量的方法[4]，这种方法平均了各局部航迹误差，并不能完全体现出各局部航迹在航迹质量上的差异，从而难以获得最优的加权因子。本文将系统航迹与局部航迹的欧氏距离以及其状态向量在1范数下的距离之和作为评价航迹质量的标准，能有效度量各局部航迹的航迹质量。而根据航迹质量来确定加权因子，则航迹质量高的局部航迹对应的加权因子大，航迹质量低的局部航迹对应的加权因子小，能保证加权因子分配的合理性和有效性。

另外，将每一路的局部航迹信息都进行融合处理的做法虽然能整合多路传感器的信息，但并没有考虑到传感器因自身差异而导致测量误差相差较大的问题。信息量越多并不能保证融合结果的精度越高[5]。因此，在进行航机状态估计融合时，本文提出设置航迹质量门限值，剔除航迹质量较差的局部航迹，将航迹质量较好的局部航迹进行融合，能有效减少异常值对融合结果的影响，从而避免传感器测量误差对系统航迹精度的影响。

算法描述：

Step1计算航迹质量

假设系统航迹集合为Ts，来自各个传感器的局部航迹集合为Tp：

其中，系统航迹集合中系统航迹数目为ns，记为：

局部航迹集合中局部航迹数目为np，记为：

假设与系统航迹xsi关联的局部航迹共m条，其中，局部航迹i表示为：

对应的系统航迹 j表示为：

局部航迹i和系统航迹 j欧氏距离定义为：

局部航迹i和系统航迹 j状态向量为：

式中，rk为航迹特征。

局部航迹i和系统航迹 j状态向量在1范数定义下的距离为：

航迹i和航迹 j的距离测度定义为：

局部航迹i在t时刻的航迹质量定义为：

Step2剔除航迹质量较差的局部航迹

设置航迹质量门限：

根据局部航迹的航迹质量和设置的门限值，删除航迹质量小于门限值的局部航迹，保留航迹质量大于等于门限值的局部航迹。

根据航迹质量分配权值，对应的权值为：

Step3加权融合

对保留的局部航迹进行航迹状态估计融合，最终得到系统航迹。加权融合航迹为：

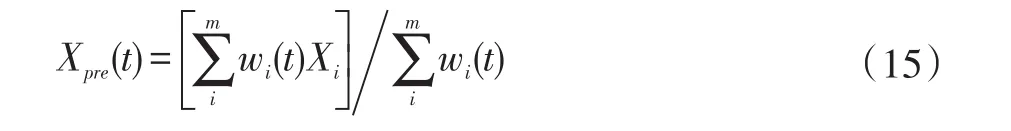
Xi是局部航迹i的状态向量，Xpre(t)为融合得到的系统航迹。

算法流程图如图2所示。

2 仿真实验

2.1 实验环境

实验模拟目标在二维空间做匀速直线运动，使用3部传感器同时观测1个目标，传感器扫描周期均为4s，且目标均在传感器观测范围之内。3部传感器周期性地输出局部航迹报告，融台程序将接收到的航迹数据先进行航迹关联处理，然后对关联成功的航迹进行航迹融合处理，最后输出融合结果。

为了验证本文算法的有效性，模拟3个具有不同测量误差的传感器，3个传感器的坐标位置以及分辨率误差如下：

S1：（-25000,10000)，δ=40

S2：(53066.6425,50000)，δ=100

S3：(10000,-83406.3881)，δ=200

并进行100次Monte Carlo航迹融合处理仿真实验，每次实验仿真测试30个周期，并计算各传感器量测值、量测融合方法输出的系统航迹及本文算法输出的系统航迹的平均误差。

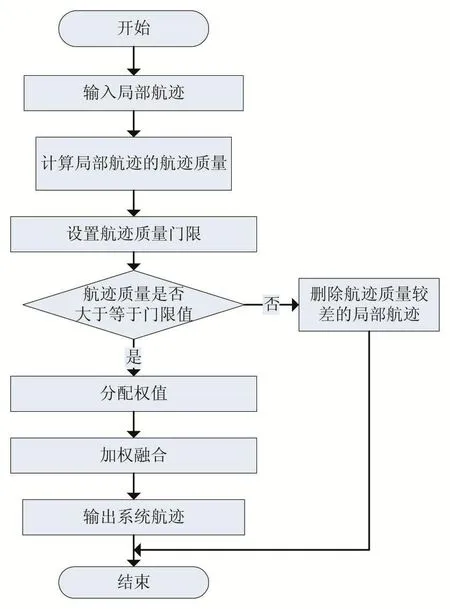
图2 融合算法流程图

2.2 仿真实验结果

表1给出了各传感器量测值、量测融合方法输出的系统航迹及本文算法输出的系统航迹的平均误差。通过量测融合以后，有效地综合了3个传感器的测量值，提高了分辨率相对低、测量误差相对大的传感器的测量效果，但是其终融合精度仍然无法高于分辨率最高、测量误差最小的传感器的测量效果。而本文算法的融合航迹误差明显降低，且低于测量误差最小的传感器的测量值。

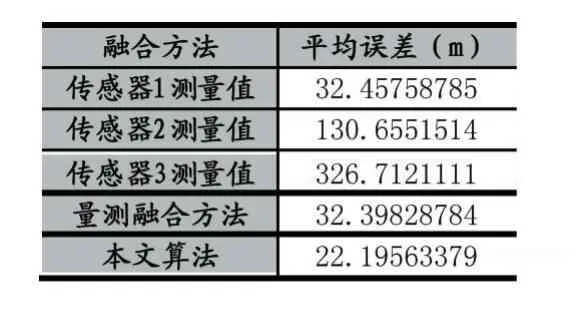
表1 平均误差

图3、图4分别给出了测量值与量测融合方法融合误差比较及测量值与本文算法融合误差比较，实验结果显示本文算法的融合精度明显高于测量融合方法的精度，且对目标状态的预估更稳定。

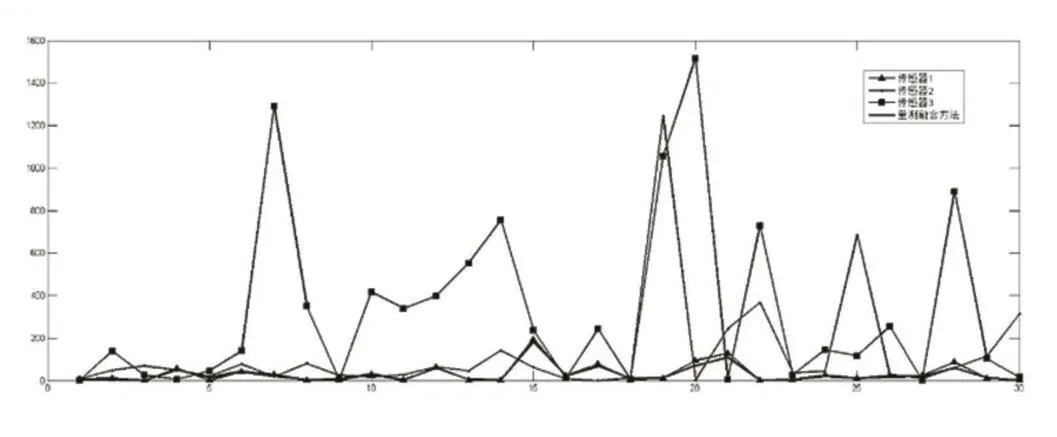
图3 测量值与量测融合方法融合误差比较

图4 测量值与本文算法融合误差比较

2.3 仿真结果分析

在分布式多传感器航迹融合系统中，多个传感器可以有效提高系统的探测能力和，但是随着传感器数量增加会影响数据传输效率，因此，考虑覆盖区域面积和避免覆盖冗余，在仿真实验中使用3部传感器。在仿真实验中分别模拟三种不同实验场景，并进行100次Monte Carlo实验，验证算法在目标密集的环境下是否有效。

以上实验结果表明，本文算法有效地综合了各个传感器的测量值，且融合输出的系统航迹精度高于单个传感器的观测值，达到了航迹融合的目的，验证了本文算法的有效性。

3 结语

量测融合方法只是将估计误差最小的局部估计作为全局估计，这种方法实际上没有对传感器航迹进行真正的融合。而本文算法基于局部航迹的航迹质量分配各局部航迹的权值，并删除了航迹质量较差的局部航迹，因而能在融合中心提取精确度更高的数据，致使融合精度大大提高。

该算法不仅计算简单便与实现，而且克服了航迹融合效果受传感器自身测量误差的影响等局限性。在三个不同的实验场景中，本文分别给出了3个传感器的量测值、量测融合方法输出的系统航迹及本文算法输出的系统航迹的平均误差，并进行了对比，实验结果验证了本文算法的有效性。

参考文献：

[1]韩红,刘允才,韩崇昭等.多传感器融合多目标跟踪中的序贯航迹关联算法[J].信号处理,2004,20(1):30.

[2]韩崇昭等.随机系统概论[M].清华大学出版社,2014:269.

[3]刘健波,王运锋.分布式雷达航迹融合关键技术研究[J].四川大学学报工程科学版,2006,38(6):119.

[4]徐丽.目标密集环境下的多传感器航迹融合算法研究[D].哈尔滨工业大学,2012.

[5]张伟,王泽阳,张可.基于多模型航迹质量的融合算法[J].计算机科学,2013(2):65-70.