基于离散指数函数优化的GM（1,1）模型在电子装备系统故障预测中的应用

孙红影

（三亚学院理工学院，海南 三亚 572022）

1 灰色GM（1,1）模型研究背景

在信息化战争理念的指引下，现代化大型舰船电子装备系统复杂程度也大幅提高。这些武器装备造价昂贵，试验维修费用极高。而在实际应用中，影响舰船电子装备故障因素的种类繁多、实验数据量较少、具有很大的随机性与不确定性。因此建立精确模型或者运用大量试验数据预测故障周期是不现实的。在实际操作过程中只能利用极其有限的试验数据对系统的故障周期进行预测。灰色GM（1,1）模型是灰色系统预测的基础与核心。其特点是能用较少的数据序列建立模型去反映系统的主要动态特性。它将系统看成一个随时间变化而变化的指数函数，因此不需要大量的数据就可以得到很好的预测效果[1-5]。在实际应用中和理论实践中，人们发现了模型的诸多局限性，对此大家都对模型进行了改进。影响模型精度的原因有很多，但主要原因还是背景值的不足[6]。

本文从背景值出发，将原有的背景值公式进行改进，并将改进的背景值公式的GM（1, 1）模型首次运用到舰船的电子装备系统的故障预测中。通过数据模拟和模型比较表明，与传统的GM（1,1）模型相比，本文改进的模型的预测精度有显著提高，能使其更好地服务于舰船电子装备系统，有十分重要的意义。

2 GM(1，1)模型背景值最优化

2.1 GM（1,1）模型及误差原因

的一次累加生成序列

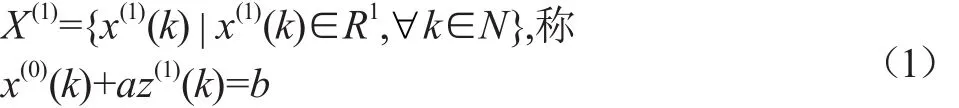
为GM(1,1)模型的定义式，也称为灰色微分方程。这里

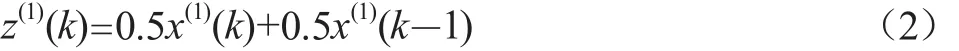
式（2）中的z(1)(k)称为GM（1,1）模型的背景值，为累加生成序列的紧邻均值生成值。

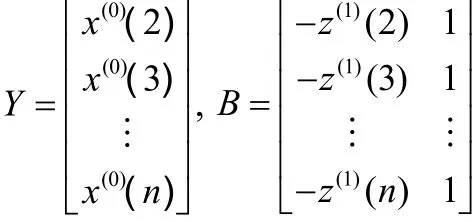
则GM（1,1）模型参数的最小二乘估计为

定义GM（1,1）模型的白化微分方程为

则灰色微分方程x(0)(k)+az(1)(k)=b的时间响应式为

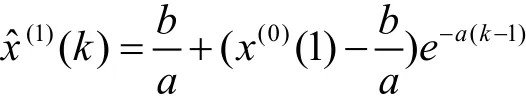
其中，k=1,2,…,n

累减还原值为

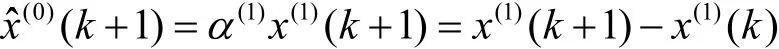
由此可见，传统的背景值计算公式实质上是用梯形公式近似的计算x(1)(t)在区间[k－1,k]上与t轴围成的面积。公式（2）是一个平滑公式，当时间间隔很小，序列数据变化平缓时，这样构造的背景值是合适的。模型偏差较小，但当序列数据变化急剧时，这样构造出来的背景值往往产生较大的滞后误差，模型偏差较大。

2.2 背景值的优化

在区间[k－1,k]上对白化方程两边求积分

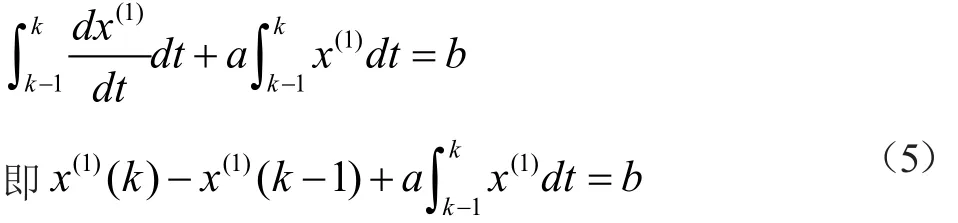
将式(6)代入z(1)(k)得

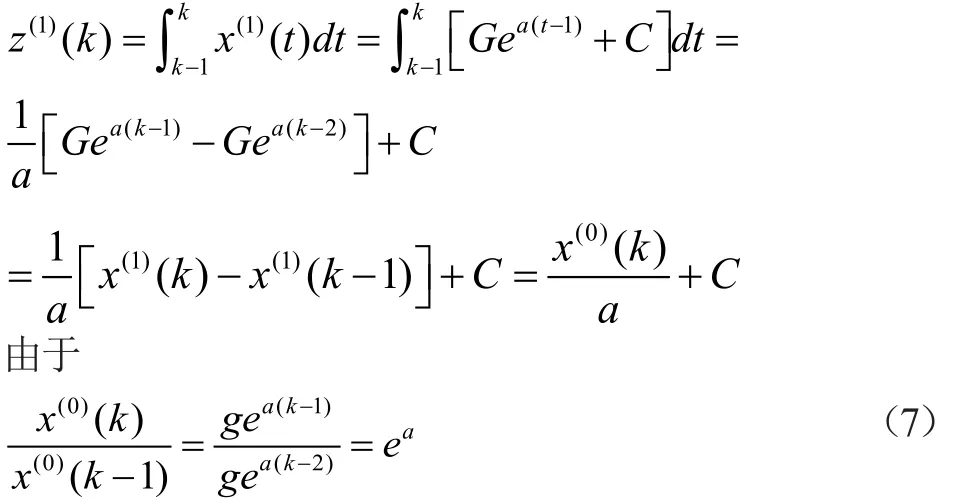
所以

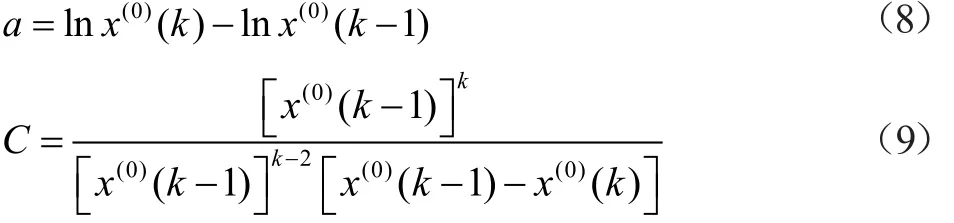
将a和C的表达式代入z(1)(k)得到新构造的背景值计算公式

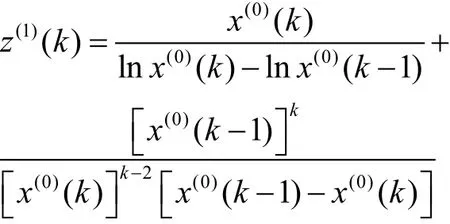
2.3 利用最优化的背景值建模

灰色微分方程x(0)(k)+az(1)(k)=b的最小二乘估计参数序列为

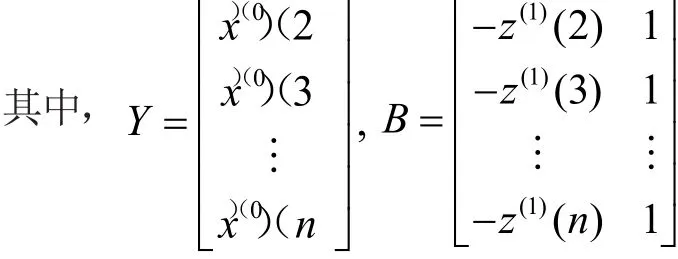
（2）灰色微分方程x(0)(k)+az(1)(k)=b的时间响应式为：

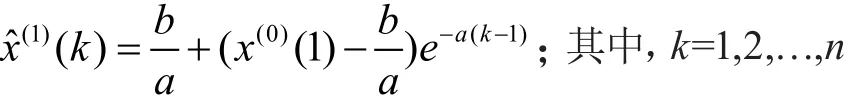
（3）还原值

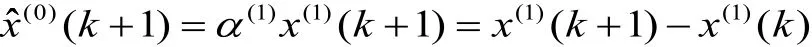
3 GM(1.1)模型在电子设备故障预测中的应用

根据文献[7]中某电子装备在高温季节的失效数据，如表1所示，选取10个连续数据作为样本。其中k表示第k次失效，t表示失效时刻。

表1 雷达累积失效时刻

运用已知的数据，运用上面优化的方法，对该装备试验过程中某次故障发生时，其失效时间进行估计。通过Matlab编程仿真，可以得到如表2所示结果。

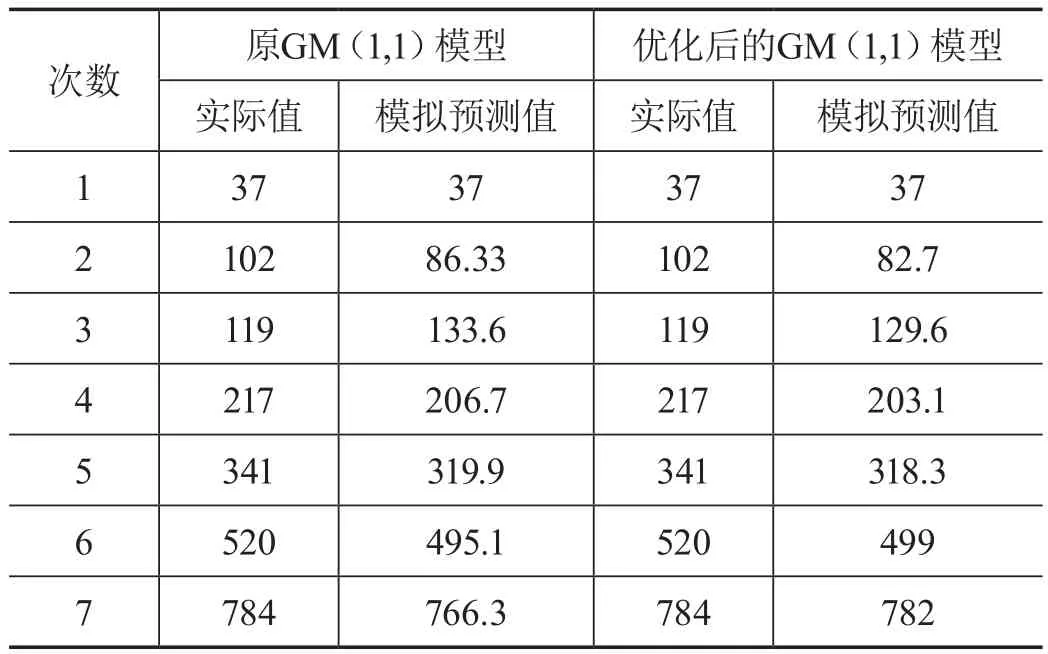
表2 两种模型的模拟预测值与实际值得比较

其中，1—5次为模拟值，6—7次为预测值。

进一步计算两种模型的模拟误差与预测误差，如表3—4所示。

表3 两种模型对故障失效时间的模拟误差（%）

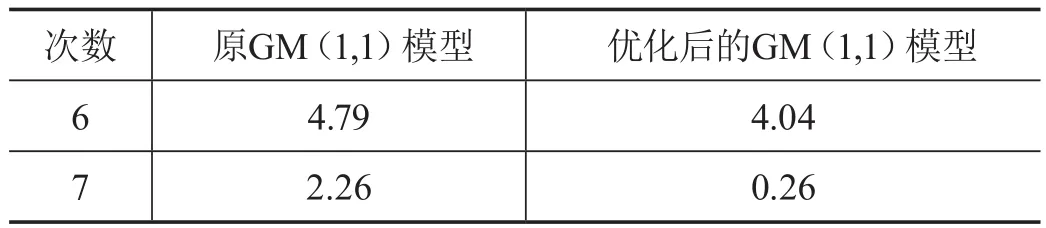
表4 两种模型对故障失效时间的预测相对误差（%）

由表3可以看出来，优化之后的模型的误差要显著地小于原GM（1,1）模型，这说明优化后的模型精度要高于原模型，这个也是模型具有较高的预测精度的前提条件：由表4可以看出，优化后的模型对第六次和第七次故障失效时间的预测相对误差为4.04%和0.26%，都小于原GM（1,1）模型。特别是第七次的预测精度达到了0.26%，从而可以看出来优化后的模型在模拟、预测方面具有的优势。

4 结语

本文通过对某电子装备在高温季节的失效数据的分析，针对数据是离散的且累加后为指数函数的特性，在传统的灰色GM（1,1）模型的基础上从背景值入手进行模型改进。通过仿真实验，将改进后的模型与传统的GM（1,1）模型的模拟精度与预测精度进行对比，得出优化后的模型的精度要高于传统的GM（1,1）模型，证明了新模型的可行性，即可提高舰船的电子系统的故障预测精度，能为装备平时的维修保养提供数据支撑，对研究武器装备的可靠性具有重大的现实意义。本文对模型的参量的选取有一定的局限性，且依赖于原始数据，对此可以进行进一步的研究。

[参考文献]

[1]邓聚龙.灰预测与决策（修订版）[M].武汉：华中科技大学出版社，2002.

[2]刘思峰，党耀国，方志耕. 灰色系统理论及其应用[M].3版.北京：科学出版社，2004.

[3]LIU S F，FORREST J.The role and position of grey system theory in science development[J].Grey System （UK），1997（4）：351-356.

[4]肖新平，宋中民，李峰.灰技术基础及其应用[M].北京：科学出版社，2005.

[5]张岐山.灰朦胧集的差异性信息理论[M].北京：石油工业出版社，2002.

[6]谭冠军.GM（1，1）模型的背景值构造方法和应用（I）[J].系统工程理论与实践，2000（5）：98-103.

[7]贾占强，梁玉英.灰色GM（1，1）模型在电子装备寿命预测中的应用[J].火力与指挥控制，2008（11）：134-143.