一种求解FDCP问题的有效算法∗

肖 宁

（陕西职业技术学院计算机科学系 西安 710100）

1 引言

模 糊 相 关 机 会 规 划［1］FDCP（Fyzzy Depen⁃dent-chance Programing），类似于随机相关机会规划，是决策者于模糊环境下以极大化模糊事件成立机会为基础把最优决策给出。FDCP问题的求解是工程应用领域中的研究热点。

在模糊环境下，FDCP模型可表示为

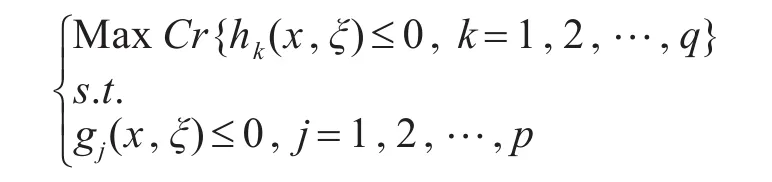
其中：ξ表示模糊向量，x表示决策变量，hk(x，ξ)≤0， k=1，2，…，q 表示模糊事件。不确定环境为 gj(x，ξ)≤0， j=1，2，…，p 。模糊事件的机会在模糊环境中和该事件相容的必要性（可能性或可信性）相等，即为不确定原理，其是求解模糊相关机会规划的理论基础。

部分管理目标与优先结构被决策者给定之后，目标函数此时能够属于极小化偏差。根据决策者给定的优先结构和目标水平，建立FDCP目标规划，其模型表示如下：

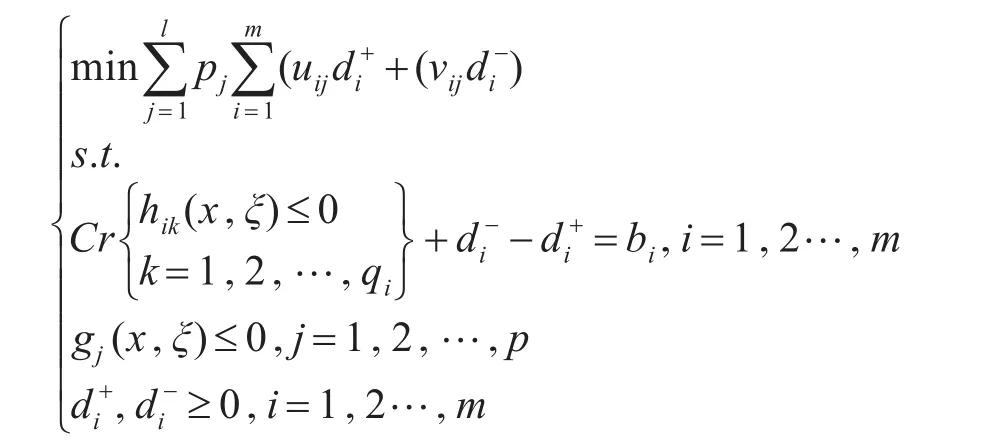
其中，系统约束个数为p；目标约束个数为m；目标i的目标值为bi；优先级个数为1；不确定环境中实值函数为gj；pj表示优先因子，表示了各个目标的相对重要性，且对于所有的j，有 pj≫pj+1；目标i与目标值偏离的负偏差为；目标i与目标值偏离的正偏差为，hik是目标约束中的实值函数；第i个目标正、负偏差（和优先级j对应）权重因子分别是 uij、vij。

FDCP问题在工程应用方面比较容易提取，但却并不容易求解，所以，很有必要研究FDCP这种高效的求解算法。目前，智能计算技术依托计算机技术的高速发展能够解决大量的复杂优化问题。处理FDCP的主要方式是利用模拟退火算法（Simu⁃lated Annealing Algorithm）、遗传算法（Genetic Algo⁃rithm，GA）、进化策略（evolution strategies）小生境技术搜索算法（Niche Technology Search Algorithms）等智能技术与模糊模拟相结合实现，而经典的遗传算法最为成功［2～8］，由于GA自身的缺点如遗传操作复杂、收敛缓慢、精度低等。更有效的FDCP问题求解途径依然是研究者们探索的重点。

受鸟群觅食过程中的群聚、迁徙行为的模拟、建模与仿真结果的研究启迪，Kennedy、Eberhart博士提出了一种高效并行计算技术——PSO（Particle Swarm Optimization，微粒群算法），它以迭代方式获取最优解。作为进化算法，它兼有进化计算与群智能的特点。它采用并行全局搜索策略，依据微粒间的协作通过对微粒适应值的评价，实现复杂空间的全局寻优，这是它不同于GA的最显著之处，该算法搜索速度快范围大、易于编程实现，对目标函数无连续、可微等苛刻条件。它已在众多的科学工程领域、学术研究方面尤其是在最优化问题的求解时展现了它的优势［10～15］。为此，将PSO算法应用于FD⁃CP问题是很有意义的研究方向，考虑到基本PSO有过早收敛的可能，为了对FDCP问题进行更精确地求解，通过SPSO（一种保证全局收敛的随机微粒群算法［9］）代替以往的GA再结合模糊模拟技术，把一种FDCP模型求解的混合智能算法形成。算法实效性经由仿真实验得以证实。

2 基本微粒群算法

在PSO中，微粒群即是D维空间中问题的潜在解的集合，微粒们依据同伴及本身的飞行经验动态调整自己的位置、速度，用适应值评价解的优劣，不断追随当前、历史最优微粒进行更新，通过不断迭代向着到最好解飞行。微粒i的第d维的速度、位置通过下式更新：

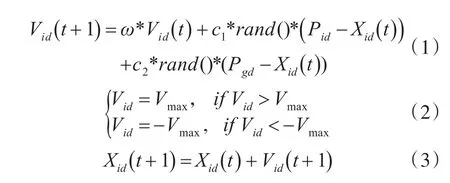
其中：均匀分布于［0，1］上的随机数为rand（）；c1、c2为加速常量；个体第d维分量（历史最优位置）为Pid；ω为惯性权重；全局第d维分量（历史最优位置）为 Pgd

3 SPSO算法

对于基本PSO算法，若ω=0，微粒的飞行速度取决于Xid(t)、Pid、Pgd，除全局最优位置微粒此时会处于静止状态之外，其余微粒均趋向自身及全局最优位置的加权中心。即微粒群将收缩至当前的全局最优处，类似于一个局部算法；若ω≠0，让微粒形成搜索范围扩展的可能，也就是具备相应的全局搜索能力。全局搜索能力与惯性权重成正比。这表明，惯性权重如果是零，式（3）所描述的公式为

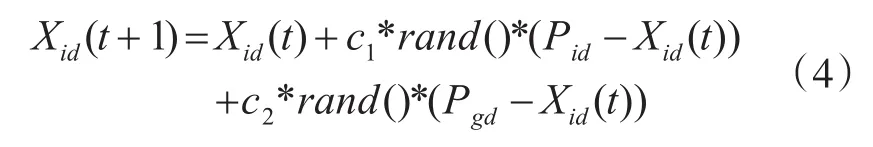
这样，式（4）在加强局部搜索能力的同时，弱化了全局搜索能力。如果Xj(t)=Pj=Pg，因为处于历史最好位置的微粒j不可以依据式（4）进化，所以经由随机产生于搜索空间内的微粒把j微粒替代，和经过Pi、Pg更新之后的其余微粒一同依据式（4）进化；如果Pg与Pj不相等，同时也没有更新Pg，那么依据式（4）进化全部微粒；如果Pg与Pj不相等，但已更新Pg，也就是在 f≠j时，Xf(t+1)=Pf=Pg，那么微粒f进化终止，于搜索空间内再次随机形成，Pi、Pg更新之后，其它微粒依据（4）式进化。此时，最少存在1个微粒j在进化的某些代会把Xj(t)=Pk=Pg满足，也就是说，搜索空间最少需重新随机形成1个微粒，全局搜索能力会因此提高。

4 模糊模拟与SPSO算法相结合的FDCP模型算法

该类问题求解过程中所采用的SPSO算法，其核心主要在于机会函数（也就是模糊事件可信性）计算，其能通过模糊模拟来完成，在寻优过程中，它主要体现在计算目标函数的适应值上。模糊模拟可信性估计算法过程现阐述如下：

如果实值函数为 f:Rn→R，n维模糊向量［可能性空间 (θ，P(θ)，Pos)上］为 ξ，那么，能通过获得可信性Cr{fL(ξ)≤0}。采用模糊模拟计算模糊事件的可信性：L=Cr{f(ξ)≤0}。

该估计算法的基本程序如下：

第1步：将θk于非空集合θ内均匀形成，且让它将 Pos(θk)≥ε(k=1，2，…，N)满足，其中ε是个充分小的数。

第2步：使得 vk=Pos(θk)，k=1，2，…，N。

第4步：返回L。

SPSO算法与模糊模拟相结合的求解FDCP的混合智能算法步骤：

第1步：微粒群初始化：如果popsize是微粒数量，那么，把1个随机数形成于决策向量x的可行域内，且对它的可行性进行检验，把该过程进行pop⁃size次重复之后，把初始可行微粒（popsize个）获得：Xi=(Xi1，Xi2，…，Xid)，i=1，2，…，popsize ，随之重新初始化群的最好位置、个体最好位置及所有微粒速度等。

第2步：所有微粒适应值的计算均采用估计算法（模糊模拟可信性）展开。

第3步：若xi(t)=pj=pg，则在搜索空间中随机机产生粒子j的位置，并计算其适应值（模糊模拟的可信性估计算法）及个体最优值，其它粒子按式（4）进化，并计算它们的适应值模糊模拟的可信性估计算法）及个体最优值。

第4步：pg如果不等于 pj，同时没有更新 pg，则以式（4）进化所有粒子。

第5步：pg如果不等于 pj，但已更新 pg，也就是说f不等于j，导致 xf(t+1)=pf=pg，那么粒子f的进化终止，把其位置重新随机形成于搜索空间内，并计算其适应值（模糊模拟的可信性估计算法）及个体最优值，其余粒子按（4）进化。

第6步：检验更新后粒子的可行性：若可行，则接受并计算它们的适应值（模糊模拟的可信性估计算法）及它们的个体最优值，如果不可行，原位置保持原状。

第7步：把全局最优微粒 pg找出。

第8步：第3步至第7步重复执行，直到有1个预设最大迭代次数或足够好的适应值。

第9步：停止迭代，把最优解、对应于最优解的最优值给出。

5 实例仿真

本文所论述方法采用文献［4］内的实例进行验证。

例1 考虑如下的单目标FDCP模型：

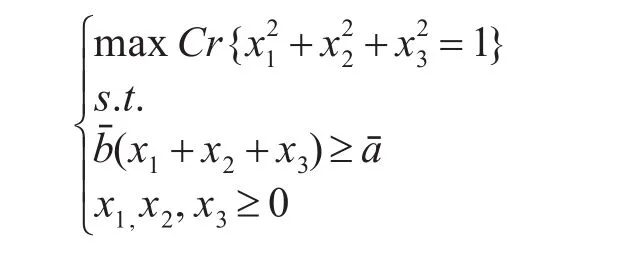
例2 考虑如下的FDCP目标规划：

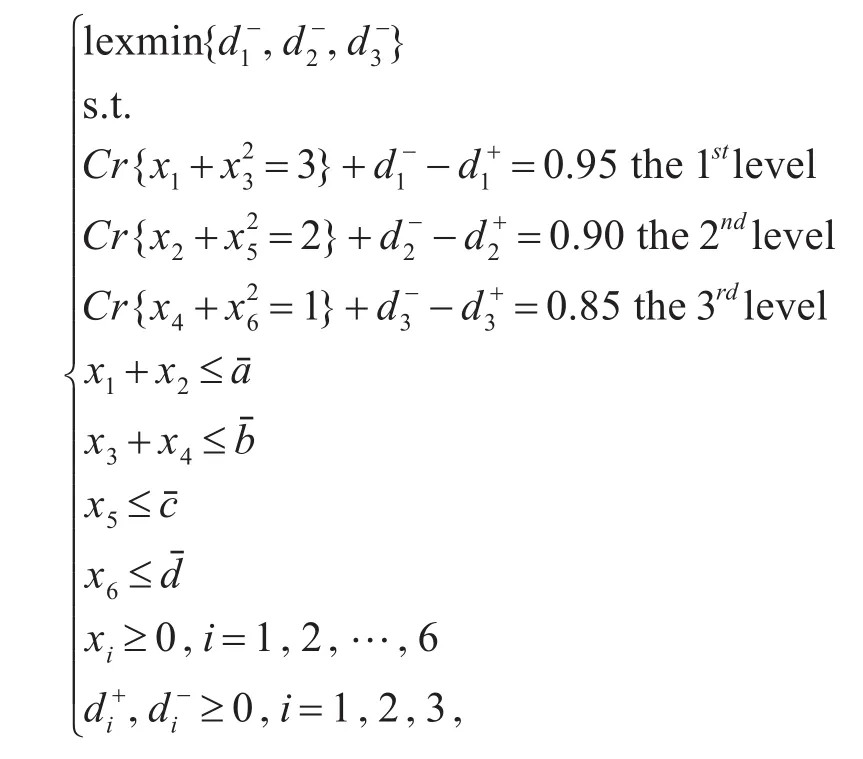
其中：μaˉ(ξ)=1/[1+(ξ-2)2]为模糊变量的隶属函数；aˉ为三角模糊变量（3，4，5），为三角模糊变量（2，3，4），为三角模糊变量（1，2，3）。

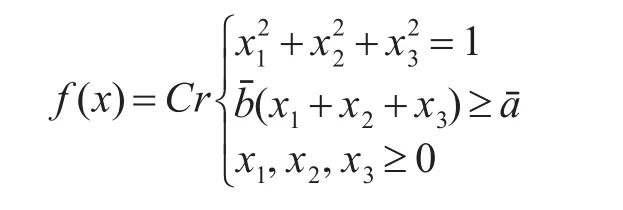
很显然可用模糊模拟来计算。

在代码中选择和文献［4］一样的运行次数1；种群规模30；迭代次数400；模拟次数5000。

在实例2中，

第一优先级中，只有一个事件x1+=3，记做ε1其支撑为：=｛x1，x3｝，相关支撑=｛x1，x2，x3，x4｝。由不确定原理，事件 ε1的机会函数f1(x)为：

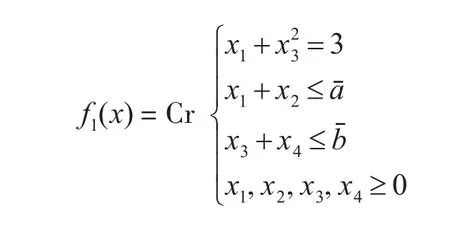
第二优先级中，也只有一个事件x2+=2，记做 ε2其支撑为：=｛x2，x5｝，相关支撑=｛x1，x2，x5｝。由不确定原理，事件ε2的机会函数 f2(x)为

第三优先级中，有一个事件x4+=1，记做ε3其支撑为：=｛x4，x6｝，相关支撑=｛x3，x4，x6｝。由不确定原理，事件ε3的机会函数 f3(x)为

很显然各个机会函数可用模糊模拟来计算。

在代码中选择和文献［4］一样的运行次数1；种群规模30；迭代次数400；模拟次数5000。

在PC机的CPU的主频：2.5GHz，内存：2GB，操作系统：winXP，VC++6.0环境下编写代码、运行程序。

在例1中：运行一次的结果如表1所示，对比文献［4］中的数据，文献［4］明显不如它的结果。如图一所示，基于迭代过程体现得更直观，把它的迭代过程进行四十次抽样。这种算法不但有极高的精度，同样有极快的收敛速度，文献［4］必需400代迭代才能获得的最优值，在这种算法中只要到第10代时便可实现。基于结果偶然因素（1次运行时）的规避，把程序进行10次运行，表2所示即为运行结果。很明显，文献［4］平均最优值明显不如采用此法所获得的结果，无论哪次均如此［4］。

在例2中：运行一次见表3，对比文献［4］中的数据，显然优于文献［4］；从程序多次运行的结果看，所有结果都优于文献［4］三个目标都满足。

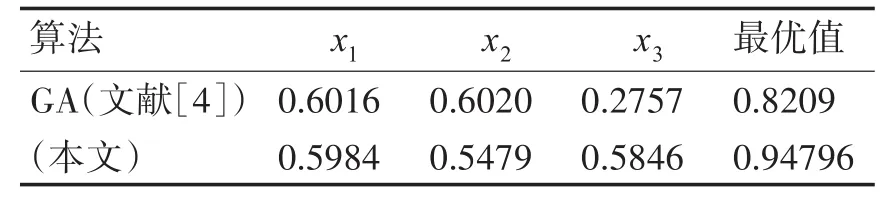
表1 实例1结果比较

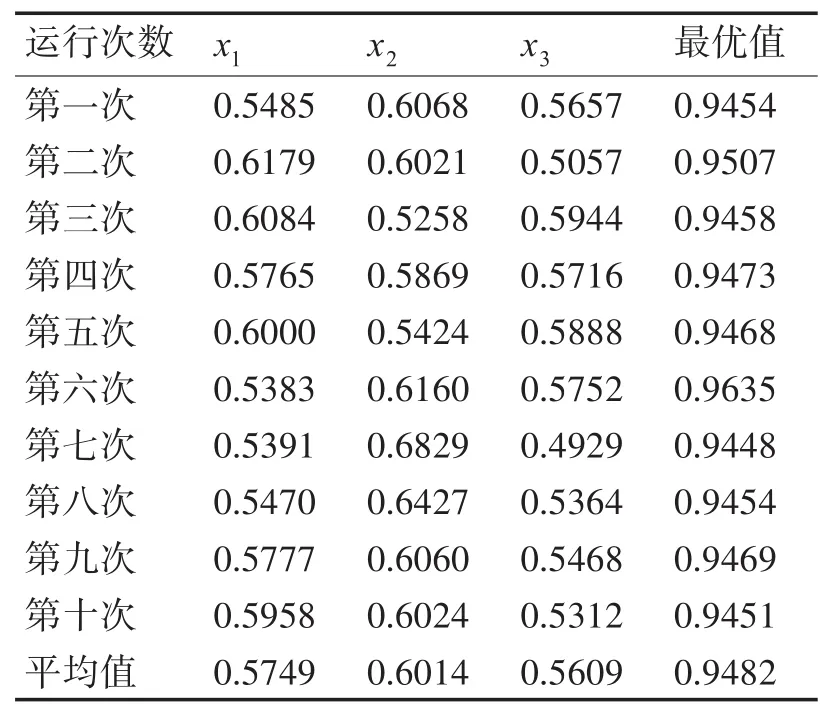
表2 实例1运行十次结果统计

表3 实例2结果比较

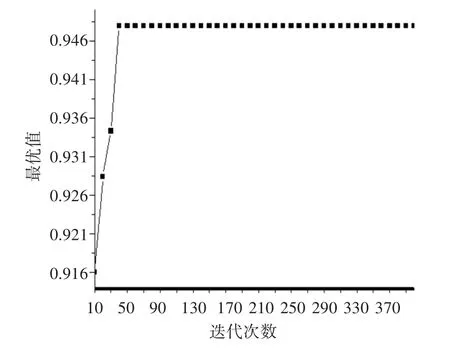
图1 实例1迭代过程抽样图

6 结语

FDCP模型问题是在实际工程应用和科学研究中都有重要意义的不确定规划问题，目前应用普遍的方法是尝试将智能算法用于该类问题的求解，混合智能算法：模糊模拟与SPSO算法求解FDCP问题是本文描述的主要内容，对比混合智能算法（基于GA算法）与实例仿真的结果表明，它存在着极为突出的优化性能；显示了该算法在FDCP问题的优势，该算法不仅对连续空间的FDCP问题求解提供了新的方法，对其它不确定规划问题的求解也有重要的指导意义，同时也拓展了PSO算法研究的应用领域。

［1］Liu B.Dependent-chance programming in fuzzy environ⁃ments［J］.Fuzzy Sets and System，2000，109（1）：97-106.

［2］Baoding Liu.Theory and practice of uncertain program⁃ming.the third edition，http：//orsc.edu.cn/liu，2009.

［3］胡永强，刘晨亮，赵书强，等.基于模糊相关机会规划的储能优化控制［J］.电力系统自动化。2014，38（6）：20-25.HU Yongqiang，LIU Chenliang，ZHAO Shuqiang，et al.Op⁃timalControlofEnergy Based On Fuzzy Correlat⁃ed-chance Programming［J］.Automation of Electic Power System，2014，38（6）：20-25.

［4］刘宝碇，赵瑞清，王纲.不确定规划及应用［M］.北京：清华大学出版社，2003.LIU Baoding，ZHAO Ruiqing，WANG Gang.Uncertain Programming and Application［M］.Beijing：Tsing Hua University Press，2003.

［5］龚树凤，龙伟军，潘明海，等.基于模糊相关机会规划的机会阵雷达方向图综合［J］.电波科学学报，2015，30（2）：201-207.GONG Shufeng，LONG Weijun，PAN Minghai，et al.Pat⁃tern Synthesis for Opportunistic Array Radar Based on Fuzzy Dependent-ohance Programming［J］.Chinese Jour⁃nal of Radio Science.2015，30（2）：201-207.

［6］裴振奎，陈继东，赵艳丽，等.混合智能算法在模糊规划中的应用［J］.郑州大学学报，2010，42（3）：71-74.PEI Zhenkui，CHEN Jidong，ZHAO Yanli，et al.Fuzzy Pro⁃gramming with a Hybrid Intelligent Algorithm［J］.Journal of Zhengzhou University.2010，42（3）：71-74.

［7］ Guangdong TIAN，Hua KE，Xiaowei CHEN.Fuzzy cost-profit tradeoff model for locating a vehicle inspection station considering regional constraints［J］.Journal of Zhe⁃jiang University-Science C（Computers&Electronics）2014，15（12）：1138-1146.

［8］陆悠悠.山东省能源经济环境系统模糊规划研究［D］.青岛：中国石油大学，2014.LU Youyou.Research on Fuzzy Programming of Ener⁃gey-economy-environment System of Shandong Province［D］.Qingdao：China University of Potroloum Master De⁃gee Thesis，2014.

［9］曾建潮，崔志华.一种保证全局收敛的PSO算法［J］.计算机研究与发展，2004，41（8）：1333-1338.ZENG Jianchao，CUI Zhihua.A Guaranteed Global Con⁃vergence Particle Swarm optimizer［J］.Journal of Comput⁃er Research and Development，2004，41（8）：1333-1338.

［10］崔志华，曾建潮.微粒群优化算法［M］.北京：科学出版社，2011.CUI Zhihua，ZENG Jianchao.Particle swarm optimization［M］.BEIJing：Science Press，2011.

［11］Zhang Liyong，Xu Jian，Zheng Yidong，Huang Zhinan，Yu Jianglong.Study on Particle Swarm Optimization（PSO）for Aircraft Parameter Identification Based on BeiDou Satellite System and Strapdown AHRS Integrated Navigation［C］//Proceedings of 2014 IEEE Chinese Guid⁃ance，Navigation and Control Conference：2269-2274.

［12］Priya C，Lakshmi P.Particle swarm optimisation applied to real time control of spherical tank system.International Journal of Bio-inspired Computation，2012，4（4）：206-216.

［13］肖宁.求解随机机会约束规划的混合智能算法［J］.计算机工程与应用，2010，46（22）：43-46.XIAO Ning.Solving Stochastic Chance-constrained Pro⁃gramming Problems with Hybrid Intelligent Algorithm［J］.Computer Engineering and Application，2010，46（22）：43-46.