水华过程水质参数与浮游植物定量关系的研究——以太湖梅梁湾为例

郭文景,符志友,汪 浩,吴丰昌 (1.北京师范大学水科学研究院,北京 100875；.中国环境科学研究院,环境基准与风险评估国家重点实验室,北京 10001)

湖泊富营养化及其可能造成的水华暴发问题可造成湖泊生态系统结构失衡和功能退化,因而一直受到关注[1-4].水华暴发中藻类产生的藻类毒素可以威胁流域内人体健康和供水安全[5-6],并可影响到湖泊的渔业价值和旅游价值,因此水华暴发一直是湖沼学研究的重点.对于水华暴发机制的探讨有助于深入理解水华暴发的过程并展开相应的控制和人为干预措施,但是对于水华暴发的发生过程以及湖泊水质参数对藻类增殖的影响一直有众多不同的研究.目前研究水华发生过程中湖泊水质参数与浮游植物的定量关系的途径主要有:基于气象/水文/营养盐指标响应的确定性的生态数学模型,对于该问题的研究从单一的营养盐限制关系逐渐发展到结合热力学或生物相互作用等的复杂系统[7-9],另一途径是基于观测数据的线性/非线性统计归纳方法,主要包括主成分分析、多元回归分析和人工神经网络等[10-13].已有研究的基本逻辑为:浮游生物指标存在对湖泊水质参数的及时响应,而不存在时间上的滞后性.随着对水华暴发过程认识的逐渐深入,湖泊水质参数和气候条件对于浮游植物增殖产生的滞后效应已有研究提及,研究[14]认为夏季常见的蓝藻在水面大量聚集的现象可能源自于春季藻类在湖泊水面下的大量增殖,在合适的气象和水温条件下,大量藻类上浮聚集形成通常意义上的蓝藻暴发.因此考虑到外界胁迫参数可能对藻类水华暴发产生的滞后效应,基于同时段检测数据的相关性分析得出的结论可能会有所缺陷,因此需要一种考虑滞后效应的数据分析方法用以研究水华暴发的过程,但截至目前,只有较少的研究将这一滞后效应考虑到目前水华暴发过程的研究中[15].

时间序列分析方法普遍用于计量经济学领域,此外近年来也常用于环境经济学领域,如探讨经济增长和环境污染的相关关系等[16-18],其包括了格兰杰因果关系检验和向量自回归模型,其通过构建考虑到自变量滞后效应的回归模型对时间变量进行拟合,可以避免无关变量之间分析导致的伪相关关系的出现,其结果具有更高的准确性和更丰富的实际意义,也可以为经济学和环境领域的研究人员和政策制定者提供有效的政策建议和决策支持.

因此本研究利用时间序列方法对太湖梅梁湾区域 2000～2012年的监测数据进行分析,建立监测数据序列的格兰杰因果关系模型和向量自回归模型,探讨水华暴发中湖泊水质参数对于浮游植物生物量的定量影响.由于上述时间序列方法对于长时间尺度的时间变量有着较为严苛的要求,首先通过平稳性检验和协整检验对获得水质参数的时间序列进行筛选,满足条件的时间序列经过格兰杰因果关系检验验证因果关系,并构建向量自回归模型,建立水质参数和浮游植物生物量之间的定量关系.

1 方法和数据处理

1.1 研究区域

太湖(30°90′N～31°54′N,119°55.3′E～120°59.6′E)是我国第三大淡水湖,位于我国经济发达的长江三角洲地区,湖泊水面面积为2427km2,平均深度为 2m,是我国富营养化程度较高的湖泊之一.太湖流域快速的经济发展和人口增长带来的污染物输入导致了太湖从上世纪七八十年代的贫营养化退化为目前的富营养化状态[19].富营养化引起的藻类尤其是蓝藻水华暴发现象时有发生,其中在2007年发生在贡湖湾的蓝藻暴发事件更是引起了公众对于城市饮用水安全的关注[20].梅梁湾位于太湖的北部,湖区水域面积为100km2,水深 1.8～2.3m.作为无锡市重要的水源地和旅游区,梅梁湾在进入 21世纪以来已经呈现了严重的富营养化状态,而水华暴发也在该区域频频出现.梅梁湾区域相对于中心湖区受太湖风浪作用的影响较小,因此该区域适合作为水华暴发的研究区域.

1.2 数据收集和预处理

监测数据来自于中国科学院太湖生态系统研究站的逐月监测数据(TLLER).梅梁湾湖区共设置 5个采样点(图 1),数据采样时间为 2000～2012年,主要检测参数为:透明度(SD),酸碱度(pH值),亚硝态氮(NO2--N),硝态氮(NO3--N),铵态氮(NH4+-N),总氮(TN),总磷(TP),水温(WT).浮游植物藻类生物量用水体叶绿素 a(Chl-a)的含量来指示.为了防止水面风速、水气交换和人为活动等因素的干扰,水样的采集在水面下0.5m处进行.上述指标的检测均按照湖泊生态系统观测标准方法进行[21].

NOx-N表示亚硝态氮(NO2--N)和硝态氮(NO3--N)的总含量.为了消除梅梁湾区域内风浪流和外源污染物造成的水质参数的差异,所有梅梁湾的逐月监测数据进行均值处理.为了消除数据可能产生的异方差波动,也为了使数据具有统计学意义,所有平均后的监测数据进行自然对数处理(pH值除外),如时间序列TN自然对数处理生成的数据记为lnTN.共得到9个时间序列,每个时间序列有n=156个逐月监测数据.

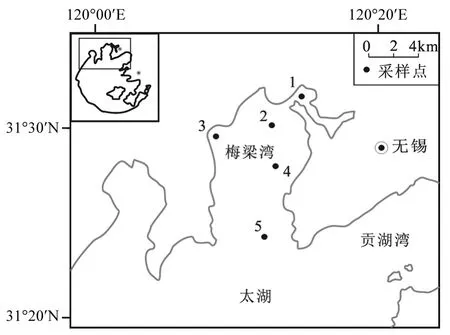
图1 太湖梅梁湾湖区监测点位置(共5个)Fig.1 Five sampling sites in Meiliang Bay of Taihu Lake

1.3 平稳性检验

Granger[22]和 Sims[23]将数据必须满足的平稳性定义为:时间序列在时间尺度上的平均值、方差和自协方差无波动.由于对不满足平稳性时间变量的相关性分析可能会导致伪相关关系的出现,并得出错误的结论,因此建立变量之间格兰杰因果关系模型和向量自回归模型的必要条件是参与的所有时间序列必须通过平稳性检验.

平稳性检验的常见方法是增广的 Dickey-Fuller test(ADF test)[24-25],其基本原理是检验时间序列是否存在单位根,如果时间序列不存在单位根,则该时间序列具有平稳性,反之,则不具有平稳性.主要基于以下回归方程进行检验:

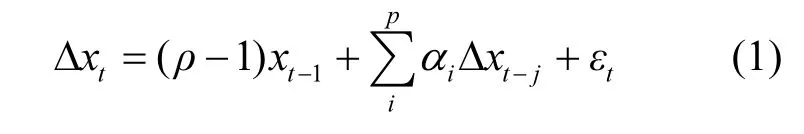
式中: xt代表时间序列的变量; t为时间;Δ表示一阶差分; ρ为单位根存在与否(赋值0或1); p代表模型的滞后阶数; αi为系数;εt表示均值为0、方差为σ2的白噪声.ADF检验的零假设设定为“该时间序列存在一个单位根”,当检验中的P值大于设定的显著性水平值,零假设被接受,该时间序列存在一个单位根,时间序列不平稳,反之,则时间序列平稳.

1.4 协整检验

对于未通过平稳性检验的非平稳序列,Granger[22]和 Sims[23]认为,因为若干非平稳时间变量的线性组合可能会保持平稳,这些非平稳变量之间仍然可以进行因果关系检验并建立向量自回归模型,但是这些非平稳变量须满足:1)时间序列为同阶不平稳,2)时间序列须通过协整性检验.其中,非平稳序列进行n次差分后的残差通过平稳性检验,则称该序列为n阶单整,记为I(n),相同阶数的非平稳序列称同阶不平稳.而协整性检验主要基于最小二乘法(OLS)进行,其方程为:

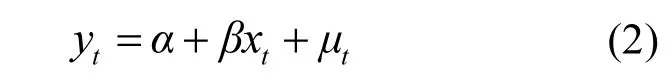
式中: t是指时间; μt表示随机扰动,如果随机扰动项μt表现出平稳性,则时间序列 yt和 xt之间具有协整性.关于协整检验的更多原理和模型方法参见 Engle[26]的文献.目前常见的协整检验的方法是Johansen-Juselius co-integration检验(JJ检验),其主要方法是通过最大特征根检验和迹检验进行判断[27].协整检验的零假设设定为“时间序列中最多存在n(n=0,1,2…)个协整方程”.

1.5 格兰杰因果关系检验和向量自回归模型

满足平稳性要求或通过协整检验后,时间序列可以建立格兰杰因果关系模型和向量自回归模型.Granger[22]从概率论的角度解释了格兰杰因果关系检验的实质:时间序列X是Y的格兰杰原因意味着在一定的滞后期内 X可以在一定程度上解释和预测Y的变化.其建立的方程如下:

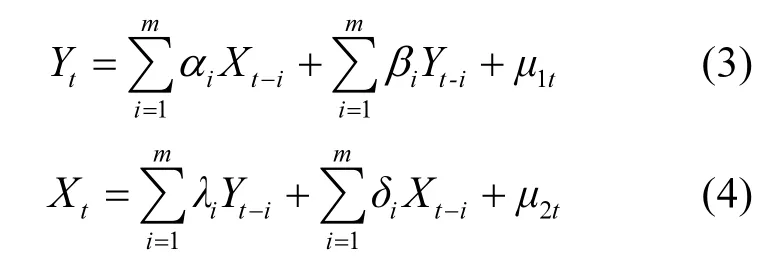
式中: αi, βi, λi和 δi为系数; μ1t和 μ2t为白噪声; m 为最大滞后阶数.格兰杰因果关系检验的零假设设定为“X不是Y的格兰杰原因”.关于格兰杰因果关系的介绍参考文献 [28].

通过了格兰杰因果关系检验的时间变量构建稳定的解释力较强的向量自回归模型(VAR),其可以定量解释时间序列之间在时间尺度上的定量关系,这一模型考虑了时间尺度上自变量对于因变量的滞后效应,因此更具有说服力.

1.6 数据分析

平稳性检验、协整检验、格兰杰因果关系检验和向量自回归模型的建立均通过常用的时间序列分析软件—Eviews(Econometrics Views 6.0)进行.在构建平稳性检验、协整检验和格兰杰因果关系模型时,零假设的显著性临界值设定为0.05.进行时间序列分析时,滞后阶数对于模型的解释能力十分重要,在本研究中,N=12确定为最大滞后阶数,而最优滞后阶数基于赤池信息准则(AIC)和施瓦茨准则(SC)确定[29-30].

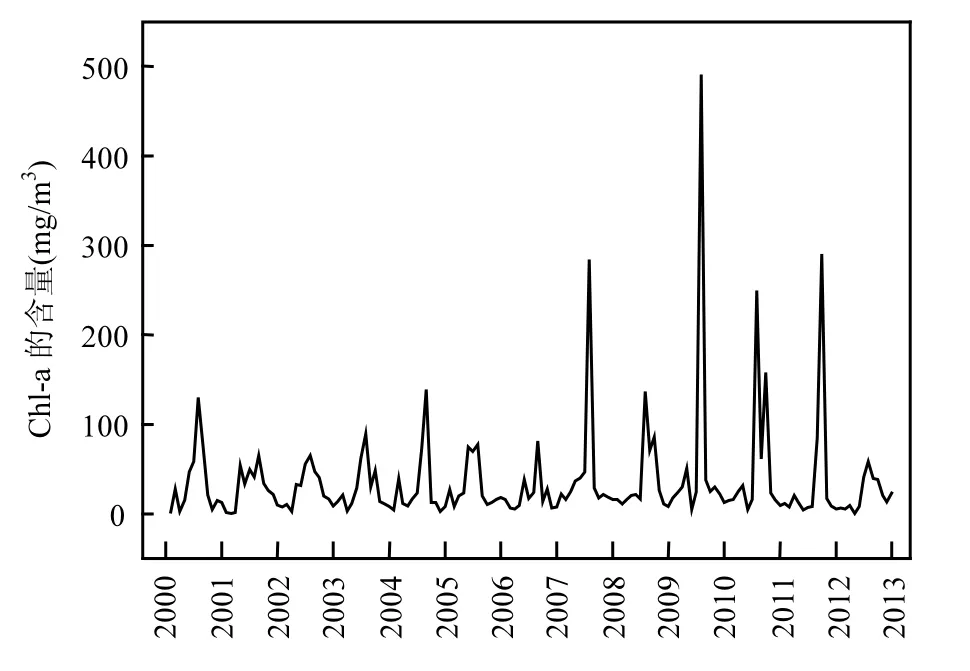
图2 梅梁湾湖区水体中Chl-a含量逐月平均数据的变化趋势(2000～2012年)Fig.2 Long-term monthly variation of concentration of Chl-a in Meiliang Bay from 2000 to 2012

图3 2000～2012年间梅梁湾区域若干水质参数逐月均值数据的变化趋势Fig.3 Long-term monthly variations of several aquatic parameters and concentrations of nutrients in Meiliang Bay from 2000 to 2012

2 结果和讨论

2.1 Chl-a浓度和水环境指标的时间变化趋势

图 2显示的是梅梁湾湖区 Chl-a含量在 2000～2012年之间的月度变化,其最小值为0.56mg/m3(2001年 2月),最大值为 491.15mg/m3(2009年7月).Chl-a含量的逐月数据在表现出波动性的同时也表现出年际的增长性,其中在夏季达到峰值,而在冬季达到最低值.湖泊水质参数的变化趋势见图3,主要趋势为在冬季和夏季达到极值.

2.2 平稳性检验结果

太湖梅梁湾区域时间序列的平稳性检验结果如表1所示,其中水质参数变量lnTN、lnSD、pH值、lnNH4+-N、lnNOx-N和lnNH4+-N/NOx-N平稳性模型的P值都小于0.05,因此零假设被拒绝,上述时间序列具有平稳性,Chl-a含量的时间变量(lnChl-a)由于零假设被接受,因此呈现出非平稳性.由于平稳性变量难以解释非平稳性变量的变化趋势,因此平稳性变量不认为是非平稳性变量Chl-a含量变化的格兰杰原因,所以lnTN、lnSD、pH值、lnNH4+-N、lnNOx-N和lnNH4+-N/NOx-N在接下来的分析中被剔除.

对非平稳序列lnTP、lnN/P、lnWT和lnChl-a进行一阶差分,并分别记为dlnTP、dlnN/P、dlnWT和 dlnChl-a.对上述序列的残差进行平稳性检验,结果表明,其一阶差分表现出平稳性,因此lnTP、lnN/P、lnWT和 lnChl-a为一阶单整变量(记为I(1)),符合进行后续协整检验的要求.

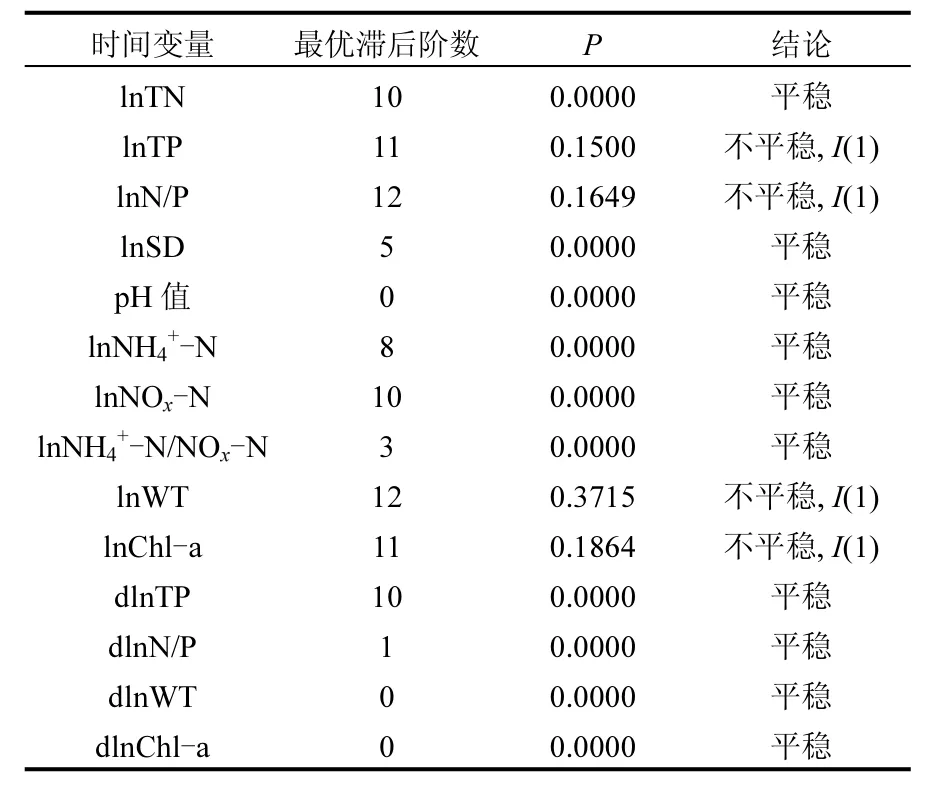
表1 梅梁湾水质参数时间序列的ADF检验结果Table 1 Results of ADF unit root test for various aquatic parameters

2.3 协整检验结果

对梅梁湾水质参数和叶绿素变量 lnTP、lnN/P、lnWT和lnChl-a进行协整分析,使用方法为JJ协整分析,通过迹检验和最大特征根检验进行判断是否存在协整关系.

表2 梅梁湾监测数据的JJ协整检验结果Table 2 Results of the Johansen-Juselius co-integration test for environmental parameters

水质参数和叶绿素变量lnTP、lnN/P、lnWT和lnChl-a的协整检验结果如表2所示,迹检验的统计值均大于 5%的临界值,迹检验和最大特征根的结果表明上述变量在时间尺度上分别存在4个和 2个协整方程,即上述时间变量之间至少存在1个协整方程.

2.4 格兰杰因果关系检验结果

对梅梁湾湖区的时间序列 lnTP、lnN/P、lnWT和lnChl-a呈现了同阶不平稳,且通过了协整检验,满足进行格兰杰因果关系检验的条件,因此使用 Eviews软件对水质参数 lnTP、lnN/P、lnWT和Chl-a含量lnChl-a的因果关系进行检验,结果如表3所示:

零假设“lnTP 不是lnChl-a的格兰杰原因”的P值为0.0001,因此该假设被拒绝,湖泊水体中TP的变化是Chl-a变化的格兰杰原因.另一个零假设“lnChl-a不是lnTP的格兰杰原因”的P值为 0.8473,零假设被接受,因此,从统计学意义上湖泊水体中Chl-a的变化不是TP变化的格兰杰原因,存在从湖泊总磷变化到 Chl-a含量变化的单向格兰杰因果关系.格兰杰因果关系的结果表明在滞后期n=2的时间尺度内,总磷的增加对浮游植物的增殖有促进作用,即表示研究区域冬季TP的变化可能会影响到春季浮游植物的生物量.

表3 Chl-a含量与湖泊水质参数变量的格兰杰因果关系检验结果Table 3 Results of the Granger causality test for lnChl-a and various independent parameters

检验湖泊水体N/P和Chl-a含量之间关系时,其零假设“lnN/P不是 lnChl-a变化的格兰杰原因”的P值为0.0098,因此lnN/P是lnChl-a变化的格兰杰原因.而“lnChl-a不是lnN/P变化的格兰杰原因”零假设的P值为0.6253,零假设被接受,lnChl-a不是lnN/P变化的格兰杰原因,因此存在长期时间尺度内的从N/P到Chl-a的单向格兰杰因果关系.

在检验湖泊水温WT和Chl-a之间的因果关系时,“lnWT 不是lnChl-a的格兰杰原因”的零假设被拒绝(P=0.0424),因此从统计学意义上水体温度是Chl-a含量变化的格兰杰原因,“lnChl-a不是 lnWT的格兰杰原因”的零假设被接受(P=0.1053),因此可以认为lnChl-a不是lnWT的格兰杰原因.因此同样存在长期时间尺度内的从水温WT到Chl-a的单向格兰杰因果关系.格兰杰因果关系结果表明在研究区域内,湖泊水温的变化可以在长期尺度上影响 Chl-a浓度,因此研究区域冬季的温度变化可能会影响次年秋季或冬季湖泊中水华暴发的强度.

2.5 向量自回归模型建立

向量自回归模型可以从时间尺度上定量检验自变量对于因变量的影响[31-32],同样使用Eviews软件建立格兰杰因果关系模型中自变量TP、TP和WT与因变量Chl-a之间的向量自回归模型(5)(括号内的数字为系数的标准差).

长时间尺度内的向量自回归模型显示,如果其他条件保持不变,水体中 TP的含量变化±1%,Chl-a的含量将会有±0.97%的变化,而1%的N/P变化只会造成0.078%Chl-a浓度的变化,1%水体温度的变动会导致0.55%Chl-a含量的变化.即水体中TP浓度对于研究区域内浮游植物生物量的变化影响较大,水温的影响次之,而N/P的影响较小.

2.6 解释和讨论

在方程(5)中,研究区域湖泊水体中水质参数TP、N/P、水温和Chl-a含量呈现了长期均衡关系.关于营养盐对于浮游植物增殖的影响一直存在争议[4,33],本研究中格兰杰因果关系检验的结果表明在研究时间段内存在单向的TP到Chl-a的格兰杰因果关系,即梅梁湾湖区 TP的浓度对水体中浮游植物生物量存在较为显著的促进作用,且对于浮游植物的影响远大于其他水质参数.在太湖的相关研究中,Guo等[34]使用冗余分析和TITAN分析研究了太湖梅梁湾和五里湖地区营养盐对浮游植物的影响,发现 TP可能是影响该区域藻类生长的限制因子.Xu等[35]通过原位实验和野外采样,估计了藻类暴发的营养盐阈值为0.20mg TP/L.在本研究区域中,营养盐的浓度为0.14mg TP/L (0.006～4.89mg/L).因此在该地区长时间尺度内富营养化过程的浮游植物增殖更多受到 TP的影响,且长时间的监测数据进一步表明TP的影响最大.对于N/P来说,格兰杰因果关系检验表明N/P存在对Chl-a浓度变化的单向影响,但是向量自回归模型的结果表示,1%的 N/P的变化只会造成 0.078%Chl-a含量的变化,相关性分析的结果也表明N/P与Chl-a浓度之间的相关关系不明显(相关系数为0.32,P＞0.05,n=156,文章中未显示).另外,研究区域内氮磷比为 35.07(0.03～127.86),高于 Redfield[36]对水体中藻类生长适宜氮磷比(N/P=16)的阈值.因此 N/P的变化并不是影响湖区中 Chl-a含量变化的主要因素.而对于水温而言,格兰杰因果关系检验的结果表明存在从湖泊水温到浮游植物生物量的单向格兰杰因果关系.温度对藻类增殖的影响早有研究提及,Abrantes等[37]研究表明温度是影响浮游植物生长的主要因素,LÜRLING 等[38]在对蓝藻增殖的研究中也得出了相似的结论.向量自回归模型的结果进一步表明在该研究区域湖泊水温对浮游植物生物量的影响要小于 TP的变化,但是远大于N/P的变化.

TP、N/P、WT和Chl-a指标在平稳性检验中呈现了不平稳性(I(1)),而梅梁湾区域其他水质参数(lnTN、lnSD、pH、lnNH4+-N、lnNOx-N和 lnNH4+-N/NOx-N)的原始数据呈现平稳性(I(0)),对于不同阶时间序列的相关性分析可能会导致伪回归的产生,并且导致错误的结论,因此从统计学意义上,上述参数不作为水体中Chl-a含量的格兰杰原因.对于氮源来说,梅梁湾区域研究时段内 TN的含量为 3.45(0.02～13.56mg/L),而在该区域的研究结果显示,水华现象发生的TN阈值为0.8mg/L[35,39].因此梅梁湾区域内氮源对于浮游植物生长的限制作用可能十分有限.而对于pH值和SD来说,本研究的结果可以解读为水体中pH值和SD的变化无法预测和影响水体中浮游植物生物量的变化,事实上水体中pH值和SD的变化可能是浮游植物增殖的结果,主要原因分别为浮游植物增殖消耗水体中CO2和HCO3-从而增加水体pH值[40]以及藻类增殖减少水体透明度.

在已有的对太湖区域藻类生物量进行模型预测工作时,陈宇炜等[10]也利用长时间的太湖水质参数和藻类生物量进行回归统计,结果发现水体中 TP和水温对于藻类生物量具有显著影响,与本文结果较为相似.邓建明等[41]利用广义可加模型和太湖监测数据,分析自变量对于因变量的非线性关系,发现除总磷和温度外,化学需氧量和电导率也是影响微囊藻生物量的关键环境因子,可能原因是模型选择的差异.在少量时间序列分析方法在湖沼学领域的应用中,Lui等[15]利用向量自回归模型拟合了香港吉澳岛附近海域叶绿素荧光与相关水质参数的时间趋势模型,该研究同样也发现了时间变量之间的滞后效应.龚绍琦等[42]使用时间序列方法中的自回归滑动平均模型(ARMA)建立了太湖不同湖区内叶绿素浓度的时间序列模型,并对一定时间内叶绿素浓度进行预测,取得了较好的预测精度.本文研究利用时间序列方法对太湖梅梁湾监测数据进行分析,发现了在一定滞后期内湖泊水质参数对于浮游植物生物量的影响,这一结论佐证了孔繁翔等提出的蓝藻水华暴发的四阶段假说-休眠、复苏、生物量增加(生长)、上浮及聚集等四个阶段[14].向量自回归模型的结果定量的阐述了在该研究区域内不同水质参数的影响大小,梅梁湾湖区水华增殖过程中,TP的变化强烈导致了水体中Chl-a的变化,说明湖泊水体中 TP的输入有利于水华暴发的形成,且 TP发挥的作用大于水体温度和其他营养盐,这可能和该流域内污染物的排放特征有关.而相对于其他营养盐(如氮源),控制流域内的P输入和湖泊内源P释放对于抑制水华暴发可能会起到更大的作用.另外水温的变化也导致了浮游植物生物量的变化,表明在长时间尺度内水温的升高可能会提高水体中 Chl-a的含量.因此在全球气候变暖的前提下水温对藻类水华暴发的促进作用暗示了在气候变暖的全球趋势下,升高的水体温度将提高该区域藻类水华暴发的概率和强度[43].

3 结论

3.1 太湖梅梁湾区域湖泊水质参数中TN、SD、pH、NH4+-N、NOx-N和NH4+-N/NOx-N不能解释Chl-a含量变化的原因,而TP、N/P和WT与Chl-a之间均存在单向的格兰杰因果关系.

3.2 研究区域内TP、N/P、WT和Chl-a含量之间存在长期均衡关系,在保持其他条件不变的基础上,1%TP、N/P和WT的变化将会导致0.97%、0.078%和0.55%Chl-a含量的变化.水体中TP的浓度在水华暴发过程中的作用可能高于其他营养盐(如不同形式的氮源),水温的影响次之.

值得注意的是,时间序列方法较少在湖泊富营养化领域中应用,其表述的因果关系可以在数理统计学上对应用的场景进行解释,同时模型的意义也需要结合实际的状况进行阐述.另外本研究由于缺少对应的水文和气象数据,因此未将上述因素考虑在内,但是水位、降水量和风力条件等因素对于水华暴发也有重要影响,因此在下一步的研究中应将这些因素考虑在内.

参考文献：

[1]Heisler J, Glibert P M, Burkholder J M, et al. Eutrophication and harmful algal blooms: a scientific consensus [J]. Harmful algae,2008,8(1):3-13.

[2]Paerl H W, Otten T G. Harmful cyanobacterial blooms: causes,consequences, and controls [J]. Microbial Ecology, 2013,65(4):995-1010.

[3]Merel S, Walker D, Chicana R, et al. State of knowledge and concerns on cyanobacterial blooms and cyanotoxins [J].Environment International, 2013,59(3):303-327.

[4]马健荣,邓建明,秦伯强,等.湖泊蓝藻水华发生机理研究进展[J]. 生态学报, 2013,33(10):3020-3030.

[5]Jochimsen E M, Carmichael W W, An J, et al. Liver failure and death after exposure to microcystins at a hemodialysis center in Brazil [J]. New England Journal of Medicine, 1998,338(13):873-878.

[6]De Figueiredo D R, Azeiteiro U M, Esteves S M, et al.Microcystin-producing blooms—a serious global public health issue [J]. Ecotoxicology and Environmental Safety, 2004,59(2):151-163.

[7]Vollenweider R A. Input-output models [J]. Schweizerische Zeitschrift für Hydrologie, 1975,37(1):53-84.

[8]Ye C, Shen Z, Zhang T, et al. Long-term joint effect of nutrients and temperature increase on algal growth in Lake Taihu, China [J].Journal of Environmental Sciences, 2011,23(2):222-227.

[9]李 博,孙冬梅,冯 平,等.于桥水库浮游藻类时空分布规律的数值模拟研究 [J]. 中国环境科学, 2013,33(3):508-515.

[10]陈宇炜,秦伯强,高锡云.太湖梅梁湾藻类及相关环境因子逐步回归统计和蓝藻水华的初步预测 [J]. 湖泊科学, 2001,13(1):63-71.

[11]Rigosi A, Hanson P, Hamilton D P, et al. Determining the probability of cyanobacterial blooms: the application of Bayesian networks in multiple lake systems [J]. Ecological Applications A Publication of the Ecological Society of America, 2015,25(1):186-199.

[12]陈云峰,殷福才,陆根法.富营养化水体水华暴发的突变模型 [J].中国环境科学, 2006,26(1):125-128.

[13]郑剑锋,焦继东.基于神经网络的城市内湖水华预警综合建模方法研究 [J]. 中国环境科学, 2017,37(5):1872-1878.

[14]孔繁翔,高 光.大型浅水富营养化湖泊中蓝藻水华形成机理的思考 [J]. 生态学报, 2005,25(3):589-595.

[15]Lui G C, Li W K, Leung K M, et al. Modelling algal blooms using vector autoregressive model with exogenous variables and long memory filter [J]. Ecological Modelling, 2007,200(1):130-138.

[16]Bozoklu S, Yilanci V. Energy consumption and economic growth for selected OECD countries: Further evidence from the Granger causality test in the frequency domain [J]. Energy Policy, 2013,63(3):877-881.

[17]Wang S, Li Q, Fang C, et al. The relationship between economic growth, energy consumption, and CO2emissions: empirical evidence from China [J]. Science of the Total Environment, 2016,542(Pt A):360-371.

[18]Xiao F, Brajer V, Mead R W. Blowing in the wind: the impact of China's Pearl River Delta on Hong Kong's air quality [J]. Science of the Total Environment, 2006,367(1):96-111.

[19]Chen Y, Fan C, Teubner K, et al. Changes of nutrients and phytoplankton chlorophyll-a in a large shallow lake, Taihu, China:an 8-year investigation [J]. Hydrobiologia, 2003,506(1-3):273-279.

[20]Qin B, Zhu G, Gao G, et al. A drinking water crisis in Lake Taihu,China: linkage to climatic variability and lake management [J].Environmental Management, 2010,45(1):105-112.

[21]金相灿,屠清瑛.湖泊富营养化调查规范 [M]. 北京:中国环境科学出版社, 1990:138-207.

[22]Granger C W. Investigating causal relations by econometric models and cross-spectral methods [J]. Econometrica: Journal of the Econometric Society, 1969,37(3):424-438.

[23]Sims C A. Money, income, and causality [J]. The American economic review, 1972,62(4):540-552.

[24]Dickey D A, Fuller W A. Distribution of the estimators for autoregressive time series with a unit root [J]. Journal of the American statistical association, 1979,74(366a):427-431.

[25]Dickey D A, Fuller W A. Likelihood ratio statistics for autoregressive time series with a unit root [J]. Econometrica:Journal of the Econometric Society, 1981,49(4):1057-1072.

[26]Engle R F, Granger C W. Co-integration and error correction:representation, estimation, and testing [J]. Econometrica: Journal of the Econometric Society, 1987,55(2):251-276.

[27]Chang C-C. A multivariate causality test of carbon dioxide emissions, energy consumption and economic growth in China [J].Applied Energy, 2010,87(11):3533-3537.

[28]曹永福.格兰杰因果性检验评述 [J]. 数量经济技术经济研究,2006,23(1):155-160.

[29]Akaike H. A new look at the statistical model identification [J].IEEE transactions on automatic control, 1974,19(6):716-723.

[30]Schwarz G. Estimating the dimension of a model [J]. The Annals of Statistics, 1978,6(2):461-464.

[31]高 山,黄 杨,王 超.货币政策传导机制有效性的实证研究——基于我国利率传导渠道的VAR模型分析 [J]. 财经问题研究, 2011,(7):50-58.

[32]高铁梅.计量经济分析方法与建模/EViews 应用及实例/数量经济学系列丛书:EViews应用及实例 [M]. 清华大学出版社有限公司, 2006:267-314.

[33]Paerl H W, Xu H, McCarthy M J, et al. Controlling harmful cyanobacterial blooms in a hyper-eutrophic lake (Lake Taihu,China): The need for a dual nutrient (N & P) management strategy [J]. Water Research, 2011,45(5):1973-1983.

[34]Guo W, Zhu Y, Fu Z, et al. Influences of environmental factors on biomass of phytoplankton in the northern part of Tai Lake, China,from 2000 to 2012 [J]. Environmental Monitoring and Assessment, 2017,189(12):608-617.

[35]Xu H, Paerl H W, Qin B, et al. Nitrogen and phosphorus inputs control phytoplankton growth in eutrophic Lake Taihu, China [J].Limnology and Oceanography, 2010,55(1):420-432.

[36]Redfield A C. The biological control of chemical factors in the environment [J]. Science Progress, 1960,11(11):150-170.

[37]Abrantes N, Antunes S, Pereira M, et al. Seasonal succession of cladocerans and phytoplankton and their interactions in a shallow eutrophic lake (Lake Vela, Portugal) [J]. Acta Oecologica, 2006,29(1):54-64.

[38]L rling M, Eshetu F, Faassen E J, et al. Comparison of cyanobacterial and green algal growth rates at different temperatures [J]. Freshwater Biology, 2013,58(3):552-559.

[39]Xu H, Paerl H W, Qin B, et al. Determining critical nutrient thresholds needed to control harmful cyanobacterial blooms in eutrophic Lake Taihu, China [J]. Environmental Science &Technology, 2014,49(2):1051-1059.

[40]Oliver R L, Ganf G G. Freshwater blooms. In B. A. Whitton & M.Potts (Eds.), The ecology of cyanobacteria: their diversity in time and space [M]. Dordrecht: Springer Netherlands, 2002:149-194.

[41]邓建明,秦伯强,王博雯.广义可加模型在 R 中的快捷实现及蓝藻水华预测分析中的应用 [J]. 生态学杂志, 2015,34(3):835-842.

[42]龚绍琦,黄家柱,李云梅,等.应用时间序列分析法对太湖叶绿素-α含量的动态研究 [J]. 海洋与湖沼, 2008,39(6):591-598.

[43]商兆堂,任 健,秦铭荣,等.气候变化与太湖蓝藻暴发的关系[J]. 生态学杂志, 2010,29(1):55-61.