研究生算法课程的分层次多样化教学研究
赵绪营,姜建锦,王志强,张晓昆
(北京电子科技学院 计算机系,北京 100070)
0 引 言
算法设计与分析是计算机专业课程体系中的主干课程,也是培养和提高学生计算思维能力的重要课程[1]。通过本课程的学习,学生能理解和掌握算法设计的主要方法,掌握算法复杂度分析的基本方法和技巧,掌握常用的算法策略及应用,理解具有代表性的算法实现案例,了解目前最新的算法研究动向,全面地理解经典算法体系和现代优化算法理论。课程目标是重点培养学生算法设计的基本能力,培养学生对算法时间与空间复杂度进行正确分析的能力,提高学生利用算法理论解决实际问题的能力,为独立分析与设计算法及优化算法打下良好的基础。
1 教学内容
算法的研究是计算机科学的核心问题之一,具有极大的应用价值和理论价值。算法的主要内容是研究计算机及其相关领域中一些非数值计算的常用算法,因此是计算机科学与技术专业限定选修的重要基础课。
1.1 知识框架
算法课程体系的主要内容以经典算法和现代智能算法的分析与设计为主,兼顾NP完全理论和概率算法,并简要介绍近似算法领域的研究成果和研究进展。算法课程的知识框架见图1[2]。
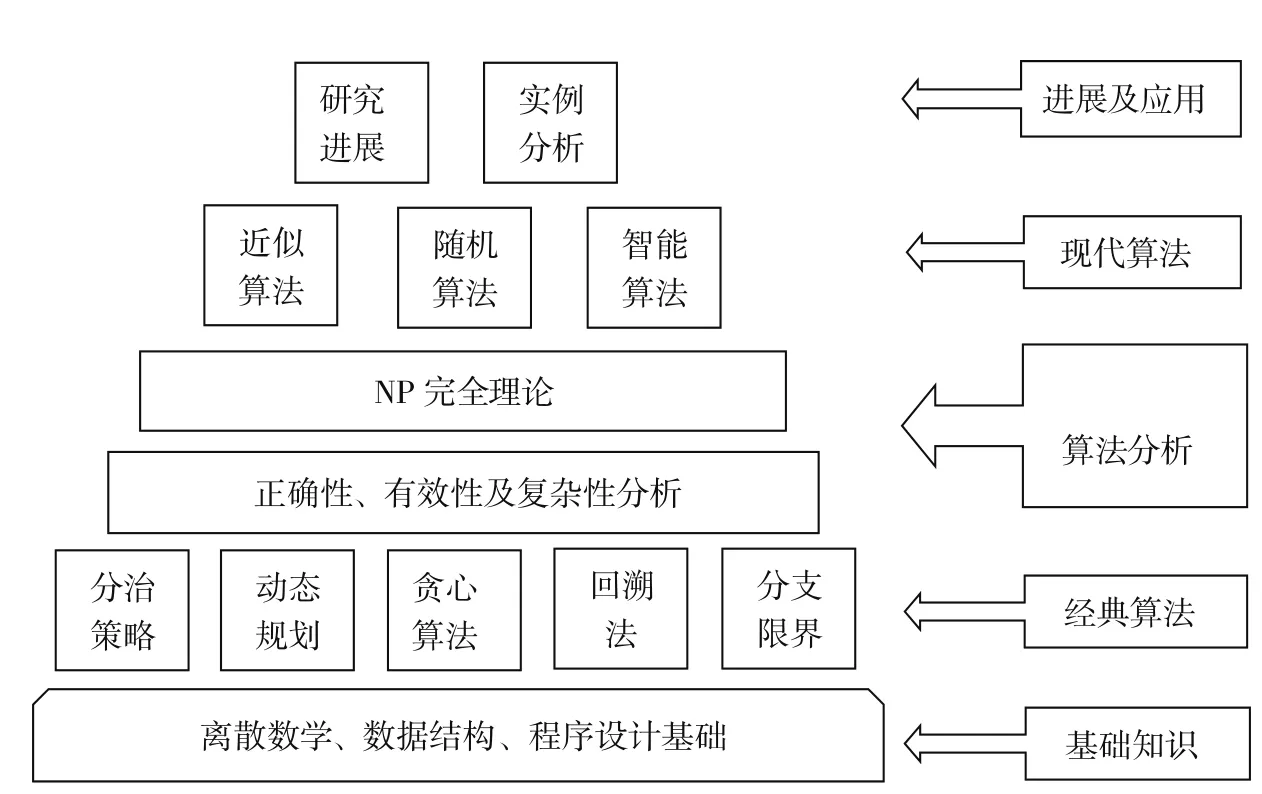
图1 算法知识框架
处于算法知识框架最底层的是算法基础知识,包括离散数学、概率统计等数学课程以及数据结构等计算机课程。按照专业培养计划,这些先导课程已经开设过。考虑到部分学生的先修课程基础不同,有些内容需要在算法课程教学过程中予以简要介绍,如离散数学课程为算法分析与设计的学习和理解打下一定的逻辑思维和数学分析的基础;程序设计基础是学生利用某种程序设计语言实现算法的基础;算法设计,特别是大型问题的算法设计,经常要用到数据结构基础等。在授课过程中,应使学生能够有机结合并融会贯通这些前序课程中学到的知识。
在算法的知识框架中,核心内容是算法的设计技术和分析方法,经典的算法策略如分治法、动态规划、贪心算法、回溯法、分支限界法等,是计算机本科专业学习的重点内容,在此基础上进一步综合与提高,在算法分析部分重点学习算法复杂度分析,简要介绍NP完全理论相关的概念和理论框架。算法知识框架的最高层次是结合算法研究进展介绍智能优化算法、近似算法、并行算法以及最新研究热点与研究动向。
1.2 重点内容
该课程重点讲解算法设计的策略、技巧、常用的方法和基本的算法分析方法以及经典的算法实现案例,逐步培养学生设计与分析算法的思维方式,引导学生提高问题抽象和建模的能力。通过本课程的教学,要强化学生理解计算机算法分析、算法设计及算法复杂度理论涉及的基本概念和基础知识,使学生掌握基本的算法分析方法和常用的算法设计方法;通过对算法实例的分析,进一步加深学生对算法设计方法的认识和理解;通过理论和实践教学环节的学习,要求学生能够应用课程介绍的方法设计软件开发中常用的或较为复杂的实际问题的算法,努力做到让算法运行快捷、求解问题有效、结果稳定,并能科学评估算法时空复杂度,提高软件设计的质量,达到培养学生扎实的专业知识和基本技能以及从事应用软件开发和测试能力的目标。
相对于本科教学,研究生算法教学的重点内容包括:①复杂性与可计算性理论,该部分内容是本科教学内容的扩展与提高;②现代优化算法,又称智能算法。现代优化算法是20世纪80年代初兴起的启发式算法,包括模拟退火、遗传算法、神经网络、禁忌搜索、蚁群算法(1992年)、粒子群算法(1995年)等。这些算法模拟大自然和人类的智慧实现对NP问题的优化求解,因此被称作计算智能优化算法[3]。智能算法或模仿生物界的进化过程,或模仿生物的生理构造和身体机能,或模仿动物的群体行为,或模仿人类的思维、语言和记忆过程的特性,或模仿自然界的物理现象,实现对问题的优化求解。智能算法在理论和实际应用方面已经得到了很大的发展,因此将其纳入研究生算法课程的重点教学内容。
1.3 参考教材
算法课程依据上述知识框架和教学内容,面向不同的学习基础,适用软硬不同的选课方向,采用分层次、多样化的课程学习结构,不指定固定的课程教材,仅给出主要的参考教材。例如王晓东的《计算机算法设计与分析》(第4版),该书是普通高等教育“十一五”国家级规划教材和国家精品课程教材。全书以算法设计策略为知识单元,系统介绍计算机算法的设计方法与分析技巧。书中既涉及经典与实用算法及实例分析,又包括算法热点领域追踪[4]。
还有《算法导论》(第3版),作者是达特茅斯学院计算机科学系教授、系主任,目前的研究兴趣包括算法工程、并行计算、具有高延迟的加速计算等。该教材将严谨性和全面性融为一体,深入讨论各类算法,并着力使这些算法的设计和分析能为各个层次的读者接受。全书各章自成体系,可以作为独立的学习单元;算法以英语和伪代码的形式描述,具备初步程序设计经验的人就能看懂;说明和解释力求浅显易懂,不失深度和数学严谨性[5]。
2 教学过程
根据算法知识框架和教学内容的安排,在教学过程中需要兼顾算法设计与分析两方面的内容,经典算法与现代算法内容形成互补,特别注重理论与应用相结合。算法策略与算法分析以及现代算法理论的内容以课堂讲授为主,算法实例和应用问题分别以教师讲述(学时比例占四分之一)、学生讨论(学时比例占二分之一)加教师点评(学时比例占四分之一)的方式进行。通过提出若干讨论问题,学生分组开展专题研究,课堂展示成果等方法,加强学生自学能力、理论联系实践能力的培养。通过实践教学环节进一步加强学生应用算法设计方法解决具体问题能力的训练,特别注意培养学生问题分析、算法设计、算法分析、算法实现、算法测试等方面的综合能力。为了配合理论和实践教学,在经典算法和现代算法学习结束后,分别布置大作业。课程作业和实验内容尽量针对不同知识基础和层次的学生给出不同的题目和要求。
2.1 注重能力培养,将计算思维渗透于课堂教学之中
算法作为一门专业基础课程,责无旁贷地担负起培养学生计算思维能力的任务。计算思维是指运用计算机科学的基础概念和方法对问题进行描述、建模和求解的思维方式,是一种普适性的科学思维方法[6]。计算思维方式不仅限于解决计算问题,还包括系统设计、人类行为的理解等问题,如何选择合适的方式陈述这些问题,以及对问题的相关方面建模并用最有效的方法实现问题求解。计算思维已经对各门学科产生了不同程度的影响,作为一个信息类的高校,计算思维能力的培养应当贯穿于大学学习的全部过程中,渗透在各门计算机相关课程里。但是,如何在具体的课程教学中培养学生的计算思维能力,目前尚没有成熟的教学指导体系。笔者努力将计算思维渗透于算法课堂教学中,在课堂讲解算法设计的策略、技巧、常用的方法和基本的算法分析方法以及经典的算法实现案例的教学过程中,注重培养学生设计与分析算法的思维方式,引导学生提高问题抽象和建模的能力。讲解经典算法实例时,通过课堂作业或提问的方式,让学生举例说明用同样的算法策略能够解决的实际问题。同一个经典问题,可以思考几种算法策略得到不同的解决方案,还要注重思考不同算法之间的区别和联系,有时还可以通过提问让学生思考在极端或特例数据的情况下某一种算法策略的适用性问题,可能超出了教材讲述的内容,但是这种方式能够激发学生的想象和创新能力。另外,根据学生的程度布置不同的任务、开展分组讨论、选取学生容易接受的课程实例等,都是算法教学值得借鉴的多样化教学模式。
2.2 以学生为主体,分层次开展实践教学
在实践教学过程中,实验性质要设置必做实验与选做实验,注意区分对待不同程度的学生,针对本科计算机课程基础或程序设计能力不同的学生,实验题目提供不同的选项和要求。信息类相关专业选修本课程的研究生自由选择实验内容以及考核形式,分别给出不同的题目和成绩评价标准。实验教学以学生为主体,教师为主导,对实验过程中出现的问题一般由学生自主研究解决,教师仅作启发性提示和引导。通过不同层次的实验内容和要求,从个性化发展的角度培养学生的计算思维能力。
2.3 开展教学科研实践活动
学校的科研与教学相结合,经常开展课外实践活动,能够为具有研究兴趣和探索精神的学生提供一个可拓展的空间。该活动适合程度较高的学生,根据个人兴趣和专长进行分组,活动的内容、目标及成果提交形式见表1。
3 课程考核
目前理论考核占课程成绩的70%,课程实践考核占20%,课程综述或最新研究进展论文占10%。为了引导学生理论联系实际,激发学生的创新能力和系统设计能力,下一步将建立更加科学的考核体系。算法课程实践部分成为课程学习与考核的重点内容,实践环节安排在课外进行,分为个人作业和团队作业两个层次,实践考核分为实践报告和课堂答辩两部分进行。个人作业是算法实践考核环节的最低要求,要求学生针对某一个问题,必须独立完成算法设计、程序实现、测试及结果分析,主要是为了培养学生基本的算法设计与分析以及实践能力。团队作业要解决的是综合性较强的问题,需要2~4人的团队协作,从建模到测试结果分析需要较强的理论和实践能力,重点培养学生的算法设计能力和团队合作精神。
4 结 语
作为特需行业的专业硕士研究生教育开展的时间较短,算法没有作为计算机应用专业研究生的核心课程,上好这门课程无疑是一个较大的挑战。目前在本科算法教学过程中取得一定的教学经验的基础上,研究生算法教学基于较高的目标进行了改进和提高。在计算机专业硕士研究生的教学与实践过程中,笔者对计算思维培养的方法进行了初步探索,将这种思维方式融入到教学的各个环节之中,并且结合专业硕士研究生的特点,提出基于分层次、多样化训练的计算思维培养方法,以提高教学效率,挖掘学生潜能,培养学生利用计算思维方式自主分析与解决实际问题的能力。
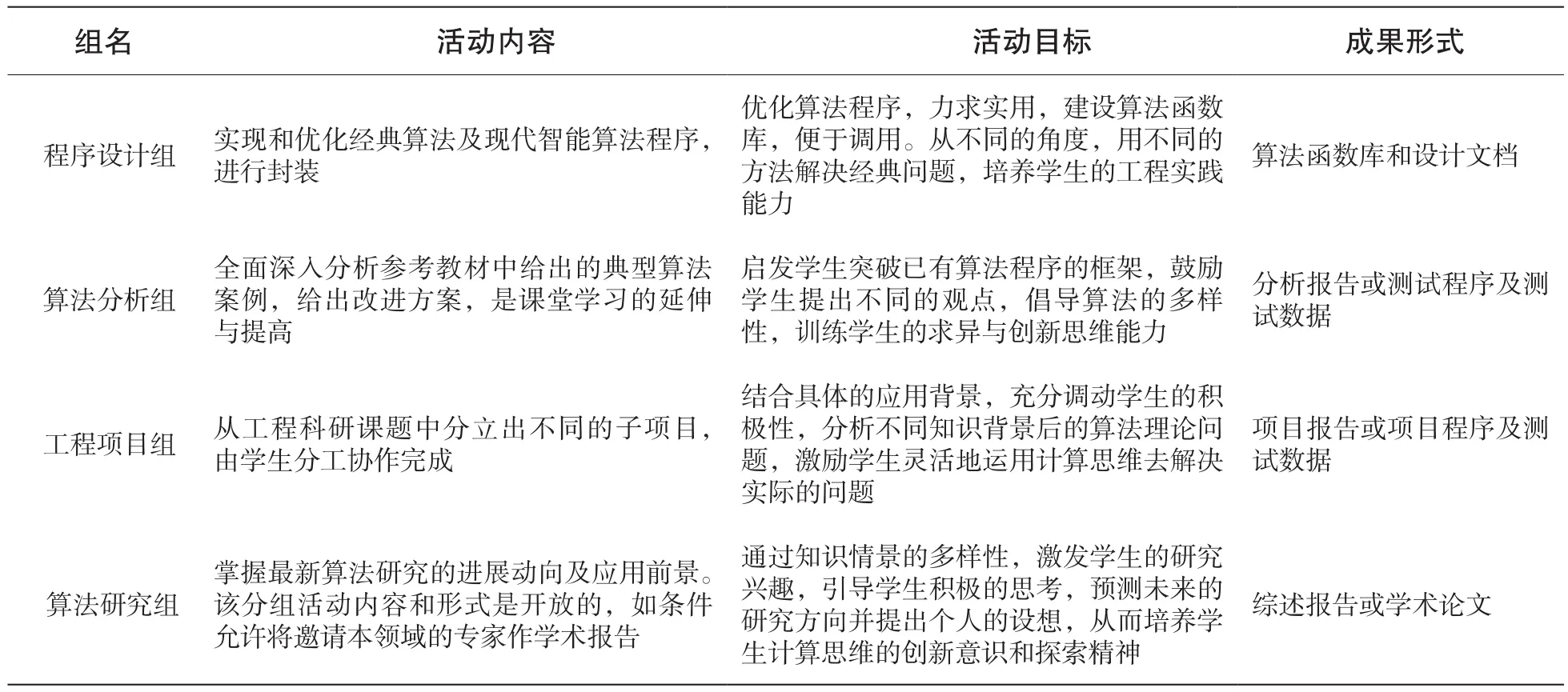
表1 教学科研实践活动分组表
参考文献:
[1]张岩, 姜建锦, 张克君. 计算机学科专业学位硕士研究生特色课程体系建设[J]. 计算机教育, 2016(12): 91-94.
[2]屈婉玲, 王捍贫, 段莉华. 面向软件工程学科的算法课程建设[J]. 中国大学教学, 2012(12): 55-57.
[3]梁旭. 现代智能优化混合算法及其应用[M]. 2版. 北京: 电子工业出版社, 2014(7): 242.
[4]王晓东. 计算机算法设计与分析[M]. 4版. 北京: 电子工业出版社, 2012(2): 306.
[5]Cormen T H, Leise C E. 算法导论[M]. 3版. 北京: 机械工业出版社, 2012(12): 780.
[6]Jeannette M W. Computational thinking[J]. Communications of the ACM, 2006(3): 33-35.

