基于误差分布估计的机器人手眼标定方法研究

,, ,

(1.中国科学院 沈阳自动化研究所， 沈阳 110016; 2.中国科学院大学，北京 100049;3.沈阳新松机器人自动化股份有限公司，沈阳 110168)

0 引言

随着智能感知和智能控制技术的发展，机器人已经逐渐融入到人们的日常生活和工作中。在机器人技术的应用中，机器人的视觉抓取是一个重要的研究课题。在机器人物体抓取中，物体位置检测的精度直接依赖于机器人手眼标定的精度。精确的手眼标定对机器人物体抓取作业的完成起着至关重要的作用。因此，提高机器人手眼标定的精度成为机器人领域的研究热点。为了解决服务机器人的手眼标定问题，可以采用高精度测量仪器测量的方法。然而，由于这些测量仪器价格高昂、操作复杂，直接测量方法未能被广泛应用。另一个可行的方法是根据机器人坐标系下和相机坐标系下相同位置对应的坐标对，估计出坐标的对应关系。

在手眼标定模型方面，Tasi和Lenz[1]采用了一种基于轴角变换的手眼标定模型。Lee[2]提出了一种基于运动估计的简化的自标定方法。Daniilidis[3]引入了一种基于对偶四元数的旋转和平移矩阵表示和计算方法。Chou和Kamel[4]提出了一种基于SVD分解的旋转矩阵计算方法。Horaud等[5]提出了通过非线性求解最小化误差模型的手眼标定方法。Fassi等人[6]则给出了一种基于几何解释的手眼标定方法，采用最小二乘方法求解。Schmidt等[7]提出了一种基于向量编码的有效数据选择方法，剔除部分无效数据，用以提高手眼标定的精度。然而，该算法的数据剔除策略较为复杂。Zhuang等[8]为机器人的手眼系统和末端执行器构造了一种整体模型。该模型的目标是最小化标定矩阵的Frobenius范数。Wei[9]则介绍了一种基于最小化代数距离的自动标定方法。王金桥等[10]和邹劲松等[11]分别采用遗传算法和自适应差异进化算法解决手眼标定求解过程中过早收敛的问题，在一定程度上提高了求解过程的可靠性。李巍等[12]在四元数理论的基础上，提出了矩阵不等式凸松弛全局最优化标定方法。为了减小数据粗差对标定精度的影响，提高机器人手眼标定精度，提出了一种基于误差分布估计加权最小二乘手眼标定方法。同时，提出的迭代求解策略可以进一步提高标定结果的置信度。

1 机器人手眼标定模型

在机器人系统中，相机的安装方式通常有两种，分别为Eye-In-Hand方式和Eye-To-Hand方式。Eye-In-Hand的方式是指相机安装在机器人手臂的末端位置，相机跟随机械臂运动；而Eye-To-Hand是指相机固定安装，机械臂的运动不会影响相机与机器人底座的相对位置关系。在服务机器人系统中，相机通常采用Eye-To-Hand的安装方式，如图1所示。Eye-To-Hand的相机安装方式可以使机器人能够获得更全面的场景信息。

1.1 基于最小二乘的手眼标定模型

(1)

在上述公式中，R和T分别表示旋转矩阵和平移矩阵。旋转矩阵R具有如下性质，即：

RTR=I

(2)

式中，I表示单位阵。手眼标定的目的是估计出旋转矩阵R和平移矩阵T。最直接的估计方法是采用最小二乘估计。针对手眼标定问题，采用最小二乘估计的优化目标可以表示为:

(3)

令:

(4)

上述F对T求偏导数，有：

(5)

式(4)取得极值的条件是使F对T的偏导数为零。令式(5)等于零，则可以计算出平移矩阵T，即有：

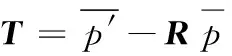
(6)

式中，

(7)

(8)

将式(6)代入式(4)，则目标函数可以表示为:

(9)

手眼标定参数中，旋转矩阵应满足如下公式：

(10)

令:

(11)

(12)

考虑到RTR=I，有：

(Rgi-hi)T(Rgi-hi)=

(13)

因此，R可以由如下公式估计得出:

(14)

式中,tr(·)为求解矩阵的迹。令S=GHT，对S进行SVD分解，有：

svd(S) =U∑VT

(15)

此时：

tr(RGHT) = tr(RU∑VT) = tr(∑VTRU)

(16)

式中，U,V和R均为正交阵。因此，VTRU也是正交阵，如果tr(∑VTRU)取最大值，则:

(17)

那么，由式(6)可解得:

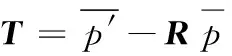
(18)

1.2 基于误差分布估计的手眼标定算法

在机器人的手眼标定中，通过相机和机器人运动学求解两种方式获得的空间中点的坐标通常存在误差。根据最小二乘估计原理，当误差服从正态分布时，最小二乘估计即是最优估计。在考虑系统存在的误差时，公式(1)改写为如下公式：

(19)

在上述公式(19)中，ε=[εxi,εyi,εzi]T是系统的误差向量。基于最小二乘估计理论，只有在误差ε服从正态分布时, 变换矩阵R和T可以用最小二乘估计方法合理计算得到。

然而，当系统误差不满足服从正态分布时，尤其是粗差存在时，传统的最小二乘估计方法的可靠性会大大下降。为了解决最小二乘估计鲁棒性低的问题，多种鲁棒估计方法(如L估计、M-估计、R估计)[13-15]被提出来。尽管这些方法能够部分解决鲁棒性低的问题，但这些估计方法的迭代过程会增加计算的时间开销。

降低最小二乘估计误差的一个直观方法是将带有粗差的数据从数据集中剔除掉。然而，判断某个数据是否带有粗差非常困难。在采用最小二乘估计方法对服务机器人进行手眼标定时，大部分测量数据包含大小相似似的误差。而数据集中带有粗差的数据的数量通常较少，同时粗差值通常远离有效数据的误差分布区间。若能根据误差的分布情况对数据提前进行甄别，则可以提高手眼标定的精度。

根据公式(17)和公式(18)，可以通过最小二乘估计方法计算得到粗糙的标定矩阵的结果R和T。之后，根据已经计算得到的R和T，对标定数据进行重构，可以计算数据的重构误差。对应于较大重构误差的数据视作带粗差数据。然而，由于有效数据与无效数据对应误差的阈值难以确定，因此仍然难以将带有粗差的数据从数据集中剔除。为此，提出了一种基于误差分布估计的加权最小二乘估计方法。通过调整数据集中数据的权重系数，降低粗差数据的影响，实现高精度的机器人手眼标定。如前所述，带有粗差的数据的数量较少，且粗差数据的重建误差远离有效数据重建误差的分布区域，因此考虑将误差分布的概率密度估计值作为原始数据的权值，从而可以使带粗差的数据的权值较小，而有效数据的权值较大。数据重建误差的概率密度分布可以通过如下公式计算得到。

(20)

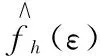
(21)

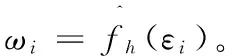
(22)

相似地，对GWHT进行SVD分解，有：

svd(GWHT) =U∑VT

(23)

类似的，根据式(17)和式(18)可以计算出标定参数中的旋转矩阵R和平移矩阵T。

采用误差分布概率密度估计的方法可以对具有不同误差的原始数据赋以不同的权重，从而克服部分粗差对手眼标定精度的影响。然而，在上述步骤中，数据重建误差分布情况与最小二乘估计标定的结果相关。因此，经初次标定后，数据重建后误差的分布略偏离真实值。为了进一步提高数据重建误差的准确度，提出了一种基于迭代策略的手眼标定算法，即重复进行基于数据重建和误差分布估计的加权最小二乘手眼标定过程。标定结果随着迭代过程逐渐收敛到最优标定结果。基于误差分布估计加权最小二乘迭代策略的手眼标定算法的流程如图2所示。

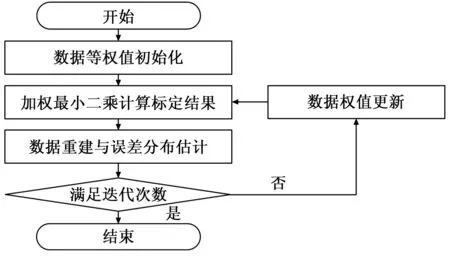
图2 可扩展手眼标定算法流程图

2 实验验证

2.1 实验设计

在服务机器人抓取应用中，为了能够提高物体抓取的可靠性，需要精确的手眼标定。为了验证所提算法对机器人物体抓取应用的适用性和可靠性，设计了相应的服务机器人手眼标定实验。在实验前，已经对相机和机器人的参数进行了标定。由于可以直接获得环境的深度信息，RGB-D相机成为机器人应用中较受关注的视觉传感器之一，并广泛应用于服务机器人的物体抓取任务。在服务机器人手眼标定实验中，在机器人末端执行器上设定视觉参考标志。示教末端执行器运动至不同的空间位置。通过RGB-D视觉传感器测量参考标志在相机坐标系下的三维坐标，同时通过运动学求解机器人末端执行器在机器人坐标系下的位置坐标。此时，可以获得一系列空间中点在相机坐标系和机器人坐标系下的坐标对。在标定实验中，共获得150对测试坐标对，其中110对坐标用于计算手眼变换矩阵，另外4组每组10对坐标数据对用于对标定结果进行验证。实验结果采用坐标重建结果误差的平均值，即重建坐标距离的平均值作为标定精度的衡量指标。坐标重建误差均值定义如下：

(24)

为了有效评估算法性能，设计了两个实验。首先，通过实验评估了迭代次数对坐标重建误差均值的影响。其次，比较了算法与现有手眼标定算法的精度。

2.2 实验结果比较与分析

2.2.1 迭代次数对坐标重建误差均值的影响

由于所提算法中迭代次数影响标定结果的精度，因此实验首先讨论了不同迭代次数对标定结果的影响。实验中，最小迭代次数为0次，最大迭代次数为10次。当迭代次数为0次时，算法退化为最小二乘算法。不同迭代次数在测试集上的实验结果如图3所示。由图3可知，随着迭代次数的增加，坐标数据重建误差逐渐减小。数据重建平均误差逐渐减小是因为随着迭代次数的增加，算法对数据重建误差的分布情况的估计越来越准确，标定结果也越来越接近真实值。良好的标定结果使得数据重建后也越来越接近真实值。另外，随着迭代次数的增加，误差减小的速率逐渐降低。当迭代次数大于等于3次后，误差均值不再发生明显改变。可以认为，手眼标定中，误差分布估计加权最小二乘方法手眼标定的合理迭代次数为3次。过小的迭代次数会使标定结果误差较大，而迭代次数超过3次则会提高标定的时间开销。

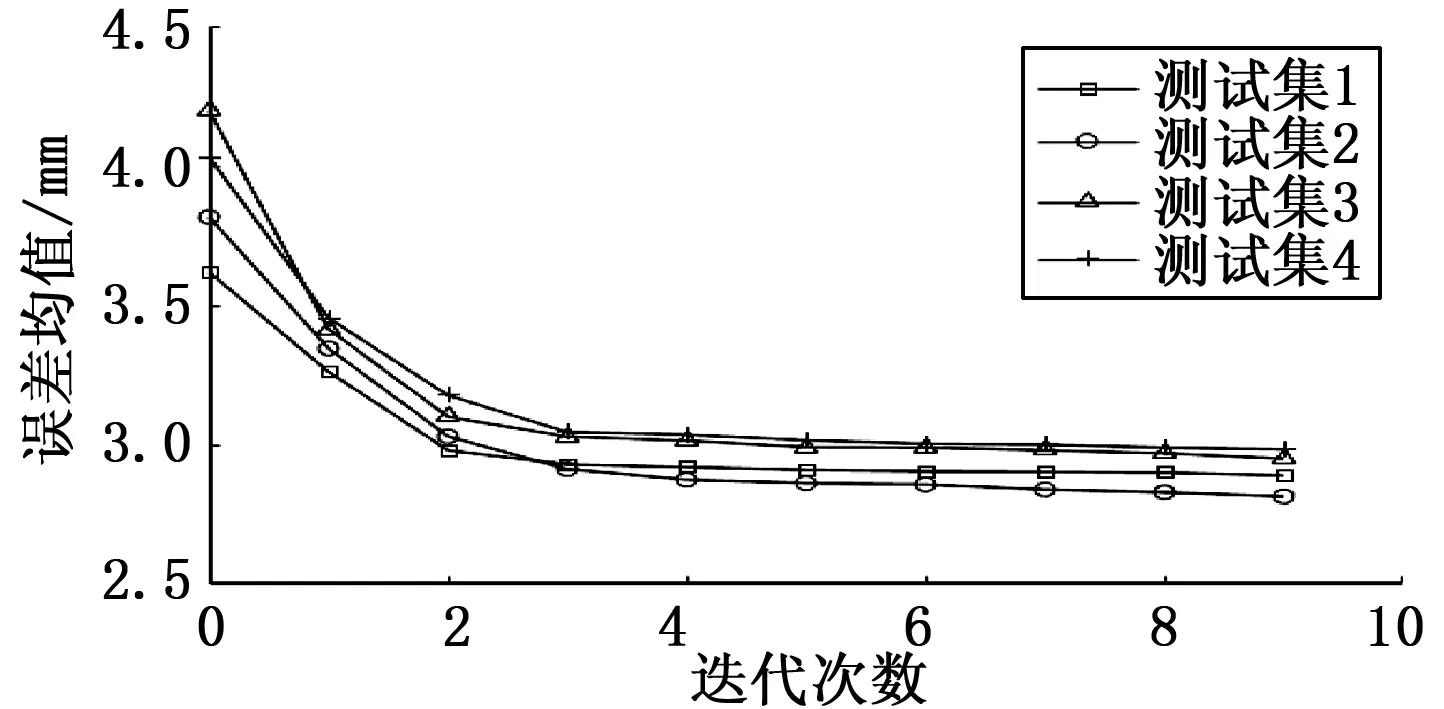
图3 粗标定数据重建误差的分布情况

2.2.2 不同标定算法对比

在实验中，分别采用最小二乘估计方法、凸松弛全局优化算法和基于误差分布估计加权最小二乘算法对服务机器人进行了手眼标定实验。其中基于误差分布估计加权最小二乘算法的迭代次数为3次。不同算法的标定结果如表1所示，坐标数据重建误差如表2所示。

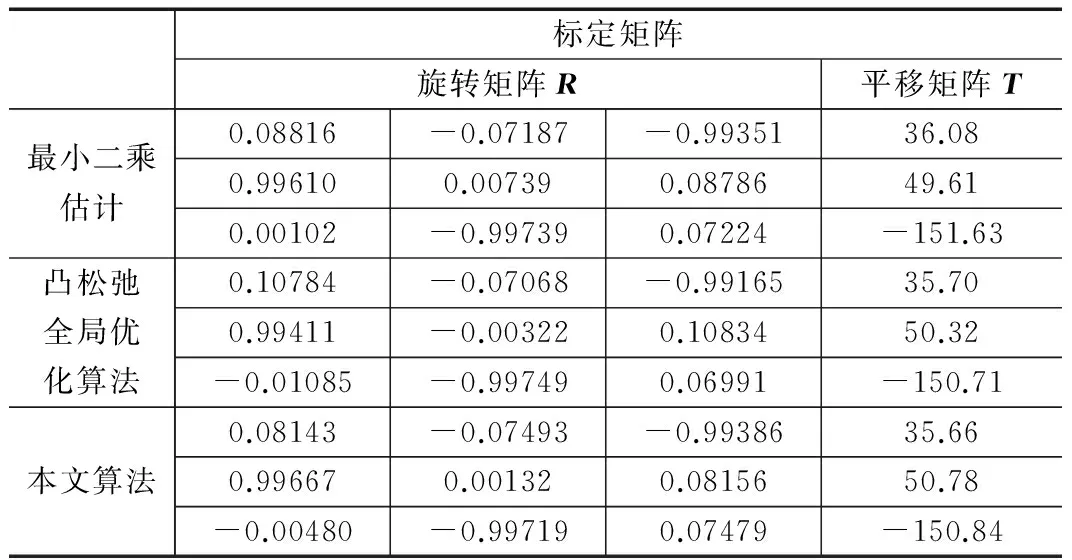
表1 不同算法标定结果对比

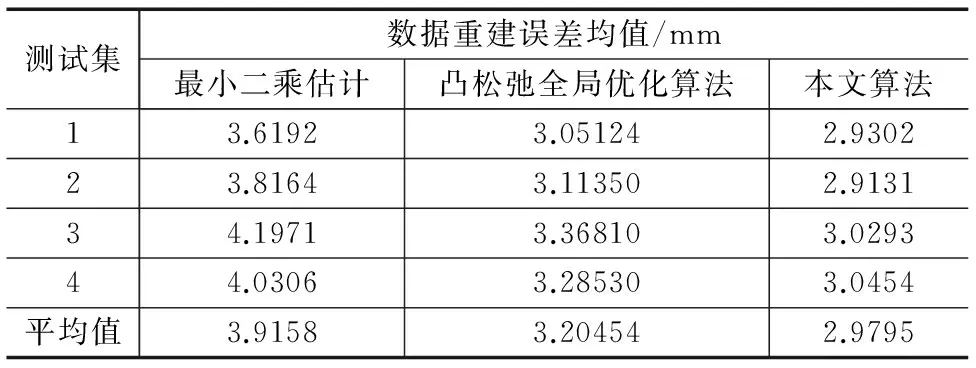
表2 不同算法测试集数据重建误差均值

由表2可知，由所提算法计算得到的标定结果对4组测试集的坐标重建误差均值比采用最小二乘估计算法和凸松弛全局优化算法的重建误差小。此实验结果证明所提算法的有效性。在服务机器人物体抓取应用中，由所提标定算法的标定精度能够满足物体抓取作业的要求。

3 结论

为适应服务机器人物体抓取任务的需求，在搭建的服务机器人物体抓取平台的基础上，对Eye-To-Hand相机安装方式手眼标定算法进行了研究。为了减小数据粗差对标定精度的影响，提高机器人手眼标定精度，提出了一种基于误差分布概率密度估计的加权最小二乘估计算法。通过粗标定结果计算原始数据的重建误差，并根据重建误差的概率密度分布为原始数据赋以相应权重，重新计算标定结果，从而有效降低带粗差数据对标定结果的影响。另外，为了解决初次标定后，数据重建后误差的分布偏离真实值的情况，采用迭代求解标定策略进一步提高手眼标定的精度。实验结果表明，所提标定算法精度高、易操作，能够满足服务机器人物体抓取的需求。

参考文献：

[1] Tsai R Y, Lenz R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration [J]. IEEE Transactions on Robotics and Automation, 1989, 5(3): 345-358.

[2] Lee S, Ro S. A self-calibration model for hand-eye systems with motion estimation [J]. Mathematical and Computer Modelling, 1996, 24(5-6): 49-77.

[3] Daniilidis K. Hand-eye calibration using dual quaternions [J]. The International Journal of Robotics Research, 1999,18(3):286-298.

[4] Chou J C K, Kamel M. Finding the position and orientation of a sensor on a robot manipulator using quaternions [J]. The International Journal of Robotics Research, 1991, 10(3): 240-254.

[5] Horaud R, Dornaika F. Hand-eye calibration [J]. The International Journal of Robotics Research, 1995, 14(3): 195-210.

[6] Fassi I, Legnani G. Hand to sensor calibration: A geometrical interpretation of the matrix equation AX=XB [J]. Journal of Field Robotics, 2005, 22(9): 497-506.

[7] Schmidt J, Heinrich N. Data selection for hand-eye calibration: a vector quantization approach [J]. The International Journal of Robotics Research,2008, 28(9):1027-1053.

[8] Zhuang H, Roth Z S, Shiu Y C, et al. Comments on" Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX= XB"[with reply][J]. IEEE Transactions on Robotics and Automation, 1991, 7(6): 877-878.

[9] Wei G Q, Arbter K, Hirzinger G. Active self-calibration of robotic eyes and hand-eye relationships with model identification [J]. IEEE Transactions on Robotics and Automation, 1998, 14(1): 158-166.

[10] 王金桥，段发阶，汪润. 精确标定关节臂视觉检测系统手眼关系[J]. 计算机工程与应用，2015，51(21):225-229.

[11] 邹劲松，黄凯锋. 一种新的三维测量机器人手眼标定方法[J]. 计算机测量与控制，2015, 23(7): 2270-2273.

[12] 李 巍，吕乃光，董明利，等. 凸松弛全局优化机器人手眼标定[J]. 计算机应用. 2017, 37(5): 1451-1455.

[13] Jiang R, Lo K M. Optimal adaptive controller for stochastic systems based on weighted least-squares algorithm [J]. ACTA Automatica Sinica, 2006, 42: 140-147.

[14] Chang L C, Jones D K, Pierpaoli C. RESTORE: robust estimation of tensors by outlier rejection [J]. Magnetic resonance in medicine, 2005, 53(5): 1088-1095.

[15] Loh P L, Wainwright M J. Regularized M-estimators with nonconvexity: Statistical and algorithmic theory for local optima[A].Advances in Neural Information Processing Systems[C]. 2013: 476-484.