基于改进无迹卡尔曼滤波的电池SOC估计

徐艳民 李剑勇

（1.华南理工大学，广州，510641，广东机电职业技术学院，广州，510515；2.山西农业大学，晋中，030800）

1 前言

安全、节能、环保是汽车技术发展的主题，随着油价的上涨和环境的污染，传统内燃机汽车的使用成本越来越高，以电动汽车为代表的新能源汽车越来越受到关注。在电动汽车使用过程中，人们最担心的还是汽车的续航能力，因而实时测试电池的荷电状态（State of Charge,SOC）显得尤为重要。

目前，电池SOC的测量方法可以分为两类，一类是基于能量守恒定律的测量方法，包括放电试验法、安时积分法、开路电压测试法[1]；另一类是基于电池模型的智能算法，以电池的电流、电压、温度等作为输入，实时输出电池荷电量，常用算法有神经网络和卡尔曼滤波[2～6]等。上述这些方法都有特定的使用条件，如，放电试验法只能在试验室条件下进行，不适用于车辆行驶过程中；安时积分法可以用于汽车行驶过程中，但电流的测量误差会随积分而不断积累；开路电压测试法只能在停车状态下进行；神经网络算法收敛速度慢，难以满足SOC估计的实时性。无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法最适用于汽车行驶过程中的SOC测量，但当SOC初始值误差较大时，无迹卡尔曼滤波收敛较慢[7]，为此，本文通过对量测噪声协方差矩阵进行设计，提出了改进的无迹卡尔曼滤波算法（Improved Unscented Kalman Filter,IUKF），此算法解决了收敛速度慢的问题，提高了SOC估计精度。

2 磷酸铁锂电池模型

2.1 电池常用模型

电池的电气模型一般分为等效电路模型和交流阻抗模型，等效电路模型主要应用于电池荷电量的估计，而交流阻抗模型主要应用于电化学阻抗谱（EIS）的分析。常用的等效电路模型有Rint模型、Thevenin模型和PNGV模型等。

2.1.1 Rint模型

电池等效的Rint模型[8]如图1所示，该模型是将电池等效为一个理想电源和电阻。图1中，Uoc等效为电池的开路电压，R等效为电池的内部欧姆电阻。Rint模型只能等效出电池的静态过程，因此只能在电池的动态过程无意义或电池的动态过程对所研究的问题无影响时使用。

图1 电池等效的Rint模型

2.1.2 Thevenin模型

电池等效的Thevenin模型[8]如图2所示，与Rint模型相比，Thevenin模型在电路中多串联了一个RC并联网络。图2中，Uoc等效为电池的开路电压，R0等效为电池的内部欧姆电阻，Rp等效为电池的极化电阻，Cp等效为电池的极化电容，Up为Rp的端电压。Thevenin模型不仅等效出了电池的静态过程，也等效出了电池的极化现象，所以Thevenin模型是对电池模型更为精确的等效模型。

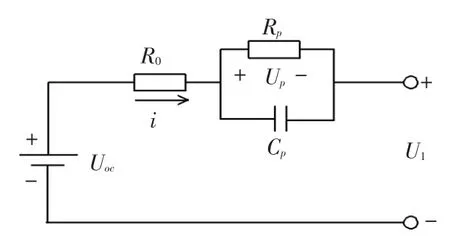
图2 电池等效的Thevenin模型

2.1.3 PNGV模型

电池等效的PNGV模型如图3所示，与Thevenin模型相比，PNGV模型在等效电路中多串联了一个电容Cb，其作用是等效出电流流过负载时引起的电压变化。图3中，Ub为电容Cb两端的电压。但是由实际情况可知，磷酸铁锂电池的输出电压非常平稳，受负载电流的影响不大，因此对于磷酸铁锂电池来说，虽然PNGV模型增加了电路复杂度，但是其等效效果与Thevenin模型相差不大。

图3 电池等效的PNGV模型

2.2 电池模型选择

为了选择磷酸铁锂电池的等效模型和确定电池模型的复杂程度，需要使用EIS分析法分辨出电池经历的电化学过程。图4为本文试验所用的锂电池在0次老化前提下的EIS分析图，图中包括在各SOC值下对电池的EIS分析结果。

图4 在不同SOC值时磷酸铁锂电池的EIS分析结果

由图4可看出，在不同SOC值下电池的EIS分析结果非常相似，都是由一个不规则的圆弧和斜线组成，不规则的圆弧是电池的极化过程，斜线是电池内锂离子在活性材料内的扩散过程，扩散过程频率较低，与汽车行驶过程中电池的高频特性不相符，所以此过程在建模中无需考虑。PNGV模型比Thevenin模型多出的电容Cb，表现在EIS分析图中应为垂直于横轴且沿纵轴正向的一条射线，但图中没有明显的射线部分，所以无需在模型中加入电容Cb。因此从模型复杂度和精确性两方面考虑，选择Thevenin模型来等效磷酸铁锂电池。

2.3 电池模型参数辨识

电池等效的Thevenin模型参数可以使用混合脉冲功率特性（Hybrid Pulse Power Characterization,HPPC）测试得到。试验所用电池最大容量为5 Ah，HPPC的单次试验是时间为60 s的放电-静置-充电过程，其中，放电过程为10 s，放电电流为15 A，静置40 s；充电过程为10 s，充电电流为11.25 A。为了得到在所有SOC值下的模型参数，每隔10%SOC测试1次。测试过程中，电池的荷电量变化很小，不足0.05 A·h，所以可以认为在测试过程中电池荷电量不变，那么辨识出的模型参数就作为当前SOC值的模型参数。

对于Thevenin模型，选择Up、SOC为状态量，记为X=[Up,SOC]T，选择U1为观测量，则根据安时积分原理和电路模型可知，Thevenin模型的状态方程为：

式中,Δt为采样间隔时间；τ=RpCp为积分时间常数；η为库伦效率；CN为当前状态下的电池最大容量。

由基尔霍夫定律可知，Thevenin模型的输出方程为：

式中，Uoc(S OC(k) )表示开路电压关于电池荷电量的函数。

利用HPPC测试方法收集电池输出数据，并使用最小二乘法对模型进行拟合后，得到模型参数如表1所示。

表1 Thevenin模型参数

由表1可知，在不同SOC值下模型的回归系数均在0.998 3以上，说明模型的拟合程度很高。

3 电池SOC估计算法

3.1 无迹卡尔曼滤波算法及其缺陷

无迹卡尔曼滤波[9]的核心是U变换，U变换的本质是一种非线性变换，U变换[10]的过程如下：

a. 对于输入变量X，给出Sigma采样策略，从而确定出Sigma点集{xi}i=1,2,…,L ，L为Sigma点数，利用输入变量统计信息给出均值权重和协方差权重

无迹卡尔曼滤波的具体步骤为：

a. 给定滤波算法的初始值x̂0、P0；

b.利用比例修正采样，计算均值权值和方差权值，计算式为：

式中，n为系统阶次；α为比例缩放因子，且有0＜α＜1；κ为Sigma点自由度，其值为0或3-n；β为先验信息，在高斯分布中取2。

c. 计算Sigma点、一步预测值和方差，计算式为：

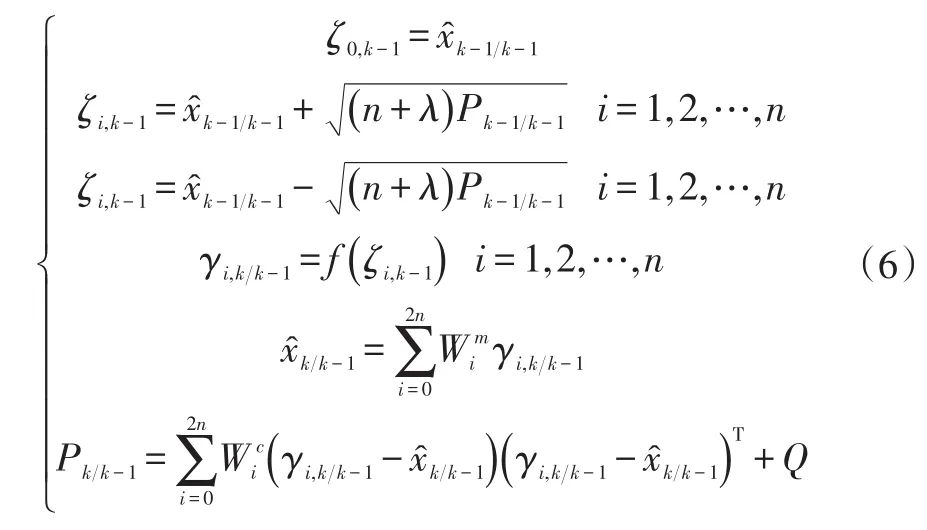
式中，f为状态传递函数；Q为状态噪声的协方差矩阵。

d.计算输出预测值和方差矩阵，计算式为：

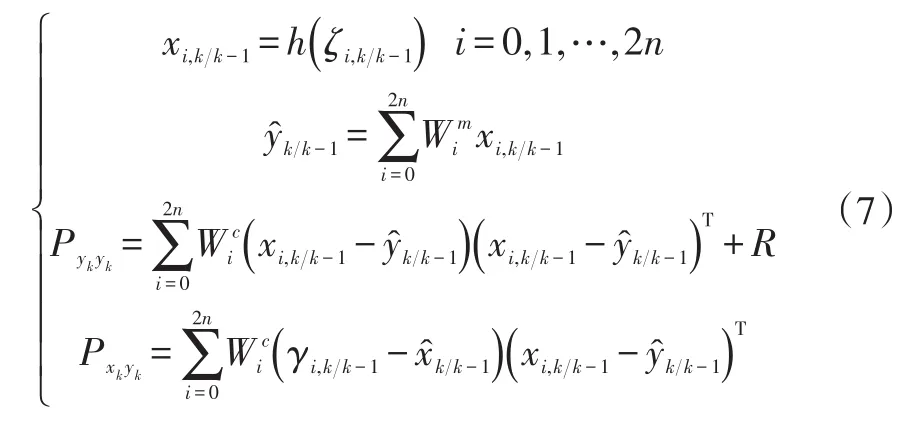
式中，h为量测函数；R为量测噪声的协方差矩阵。

e. 修正值的计算，计算式为:

利用无迹卡尔曼滤波算法对电池SOC进行估计，初值设置为 P0=E2×2，Q=diag(1 0-8,10-8)，R=2.5×10-5，当SOC初值误差分别为0.2、0.3时，UKF对电池SOC估计结果如图5所示。

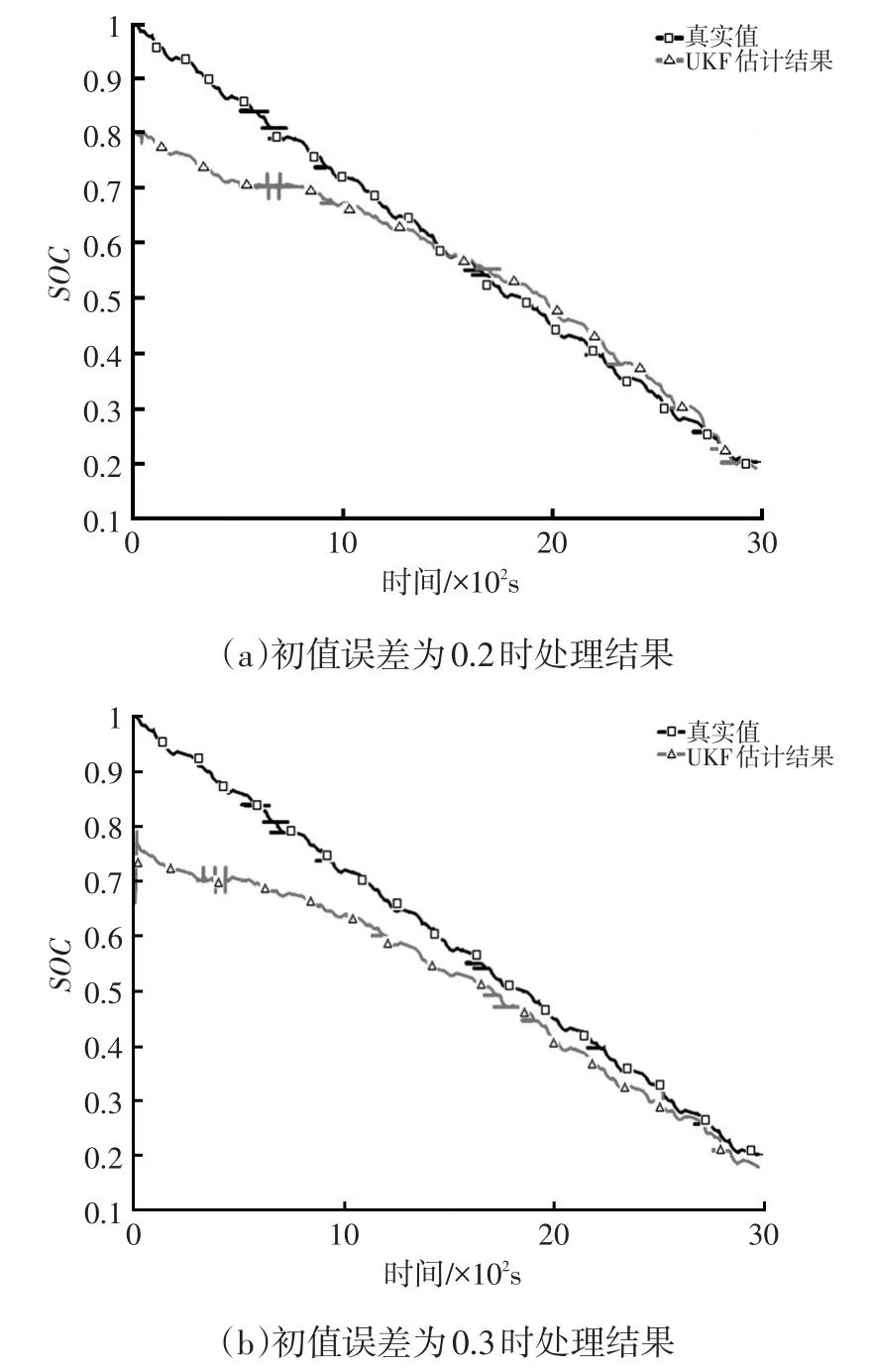
图5 UKF对电池SOC估计结果

由图5可看出，当SOC存在初值误差时，无迹卡尔曼滤波都最终收敛，但是存在收敛速度较慢的问题，在汽车行驶过程中对电池荷电量估计误差较大。

3.2 改进的无迹卡尔曼滤波算法

为了解决无迹卡尔曼滤波收敛速度慢的问题，使其尽快接近真实值，提出了改进的无迹卡尔曼滤波算法。由式（8）可知，通过调整修正系数K可以改进收敛速度，由式（7）和（8）可得：

由式（9）可知，通过调节量测噪声R可调整修正系数的大小。通过试验可知，当R较大时，收敛速度较慢，但收敛后较稳定；当R较小时，收敛速度较快，但收敛后震荡较大。所以可以先使用较小R1值使算法快速收敛，然后使用较大R2值使算法稳定。无迹卡尔曼滤波的改进原理如图6所示。

4 算法验证

4.1 仿真验证

同时使用无迹卡尔曼滤波和改进算法对SOC初值误差分别为0.2、0.3时进行SOC估计。采用改进算法时的取值为：R1=10-6，Rz=10-4，t0=650 s，估计结果如图7所示。

图6 无迹卡尔曼滤波的改进原理

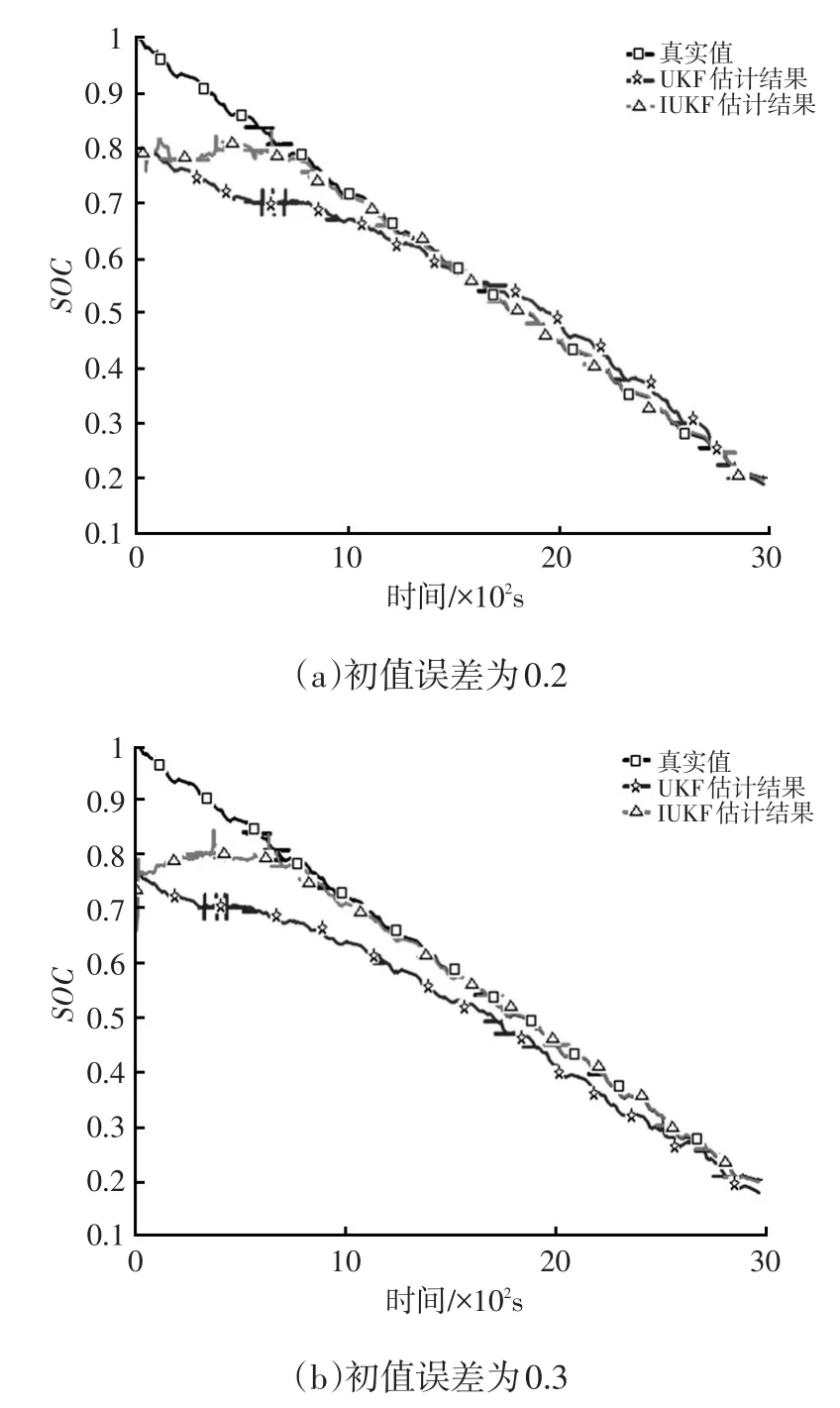
图7 两种算法对电池SOC估计结果

从图7可看出，改进的无迹卡尔曼滤波算法比原算法能够更快地接近真值，而且收敛精度也更高，这验证了改进的无迹卡尔曼滤波克服了原算法的缺陷。

下面利用改进算法对电池老化过程中的SOC值进行估计。

4.2 老化过程电池SOC估计

在电池老化过程中，电池容量会不断衰减，所以需要首先建立容量与老化次数之间的函数关系。以1.5 A的电流对电池进行充、放电使其老化，共试验600次，使用二次函数对试验数据进行拟合，得到拟合函数为：

式（10）的拟合度为0.994 3。下面以老化次数100次和200次为例，使用改进算法对电池SOC进行估计，结果如图8所示。

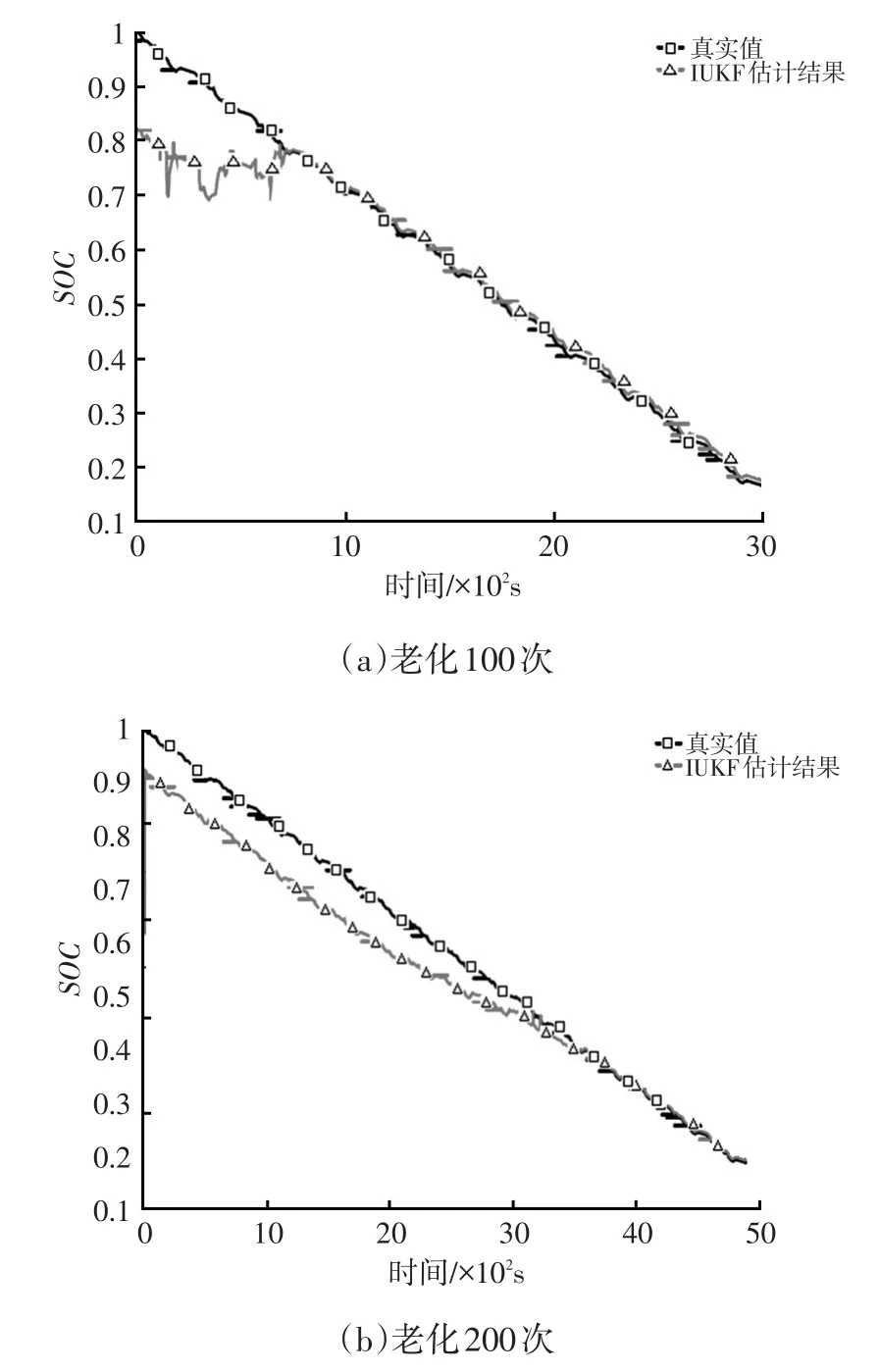
图8 不同老化次数时改进算法对电池SOC估计结果

由图8可看出，在SOC初值误差较大时，基于改进算法的SOC估计值能够迅速收敛至真值附近，而且收敛后的估计误差都在4%以内，具有很高的SOC估计精度。

5 结束语

本文针对电池SOC初值误差较大时，无迹卡尔曼滤波收敛较慢的问题，提出了改进的无迹卡尔曼滤波算法。通过试验可知，改进算法不仅克服了原有算法的缺陷，而且提高了估计精度；使用改进算法对老化过程中的电池进行SOC估计，估计值能够迅速收敛至真值附近，且最大估计误差在4%以内，完全满足电动汽车的使用要求。

[1]Pop V,Bergveld H J,Notten PH L,et al.State-of-the-Art of Battery State-of-Charge Determination.Measurement Science and Technology,2005,16(2):R93.

[2]黄耀波，唐海定，章欢，等.基于遗传神经网络的电动汽车锂电池SOC预测[J].机电工程，2013，30(10):1255～1258.

[3]米林，赵孟娜，秦甲磊，等.基于径向基函数神经网络的电动汽车动力电池SOC模型[J].重庆理工大学学报（自然科学版），2011，25(10):1～5.

[4]游双.镍氢电池组SOC神经网络估算策略研究[D].天津：天津大学,2007.

[5]韩忠华，刘珊珊，石刚，等.基于扩展卡尔曼神经网络算法估计电池SOC[J].电子技术应用,2016,42(7)：76～78，82.

[6]冯光.基于EKF的锂离子电池SOC估算的建模与仿真[D].武汉：武汉理工大学,2013.

[7]胡小军.基于无迹卡尔曼滤波的动力锂电池SOC估计与实现[D].长沙：中南大学,2014.

[8]林成涛，仇斌，陈全世.电流输入电动汽车电池等效电路模型的比较[J].机械工程学报,2005,41(12):76～81.

[9]黄铫，张天骐，高清山,等.一种提高无迹卡尔曼滤波精确度的方法[J].计算机仿真,2010,27(3):348～352.

[10]黄海兵，张进.基于U变换的空间站交会调相非线性协方差分析方法.国防科技大学学报[J],2014，36(2):18～23.