基于构件分组的预制装配式生产资源优化

张 云

(武汉理工大学土木工程与建筑学院，武汉 430070)

我国大力推行建筑工业化，特别是发展装配式建筑，相比现浇结构，装配式建筑增量成本大约在200～500元/m2[1],其中预制构件生产费用占据较大比例，降低预制构件生产成本成为目前亟待解决的问题。

装配式构件生产建造流程包含设计、构件拆分、生产、运输和现场装配，如何在全生命周期下降低建造生产成本尤为重要。过去的研究主要集中分析装配式增量成本因素,从宏观管理层面给出了较多建议[2]，陈伟对装配式多维空间下资源调度进行优化[3],但对于装配式预制构件成本控制的核心——设计阶段构件拆分研究较少。在工业化领域的一项全面的文献综述表明，如果能够生产更复杂的预制构件或模块而不是单个的建筑元素(Girmscheid 2010)[4]，可以将更大的价值添加到预制项目中。

该文引用一种构件分组的思想，将模具作为一种重要的生产资源进行优化，与生产限制和施工需求相结合，最大化模具利用率和周转次数。

1 构件分组概念

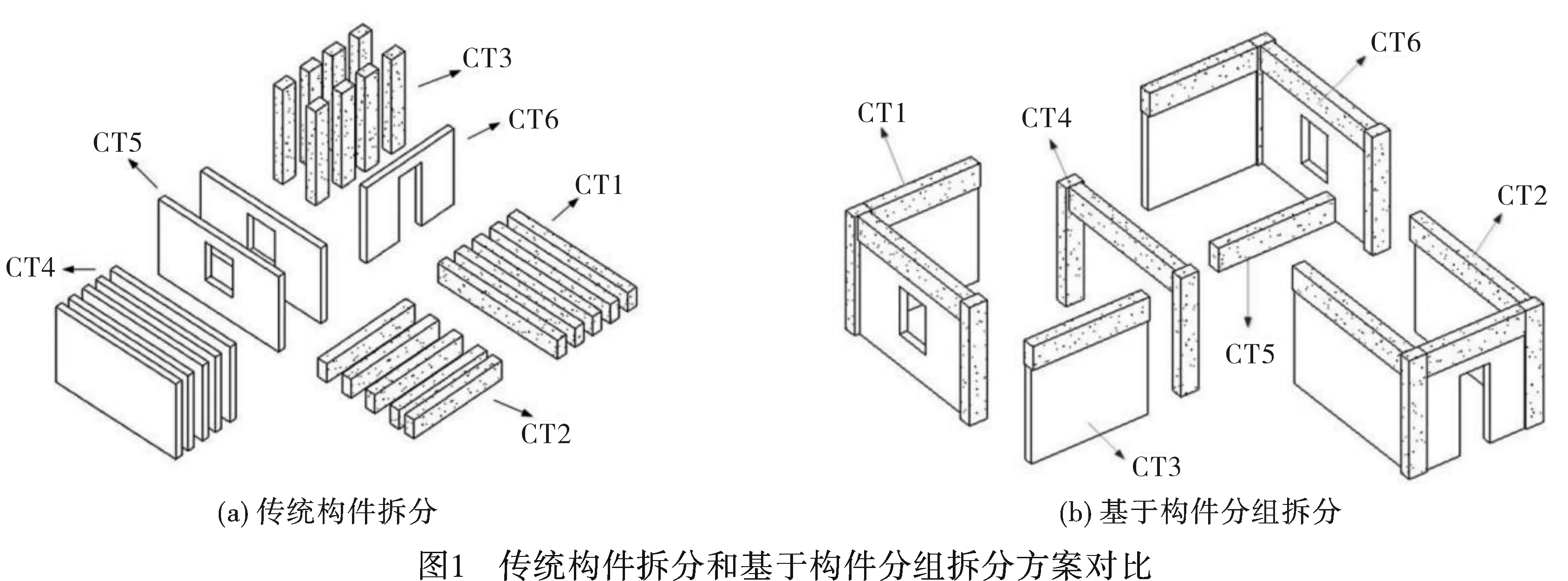
构件分组的定义为，在一个生产周期内，一个特定模具所能生产多种类型的结构构件的一个集合。传统装配式建筑生产拆分构件如图1(a)所示，单个构件制作简单，构件类型多样，数量多，综合考虑模具及生产成本、运输成本、吊装成本，在总体上并不一定是最优的。基于构件分组的拆分方法如图1(b)所示,构件类型和模具类型是一个多对多的关系，用两个矩阵CTG和MA来表示构件分组的概念。矩阵CTG表示一个构件分组的构件类型组成部分，矩阵MA描述每个模具类型生产不同的构件分组的能力。

2 问题阐述

假设一个预制构件厂(F)收到一组构件订单并且需要结合模具使用情况制定最佳的生产计划。结构包含J种构件类型(j=1,2,...,J)。每个构件类型(j)对应一个专用的生产模具(i)，所以专用的模具类型总数I=J。生产厂可能需要生产并使用好几个某一类模具来满足建造要求。因此符号l(l=1,2,...,nl)定义每个模具类型的实例个数，nl表示每类模具的最大数，符号h(h=1,2,…,H)用来表示每个构件分组。整个结构的构件分组总数是H。

如图2所示，该文定义了规划范围，浇筑周期，每天运输量和建造周期。在每个建造周期t(t=1,2,...,T)规划所需构件生产量和运输量。一个建造周期(t)定义为一个标准层所需的构件预制。项目计划(P)被分成T个完全一样的小节段，T表示建造周期数。

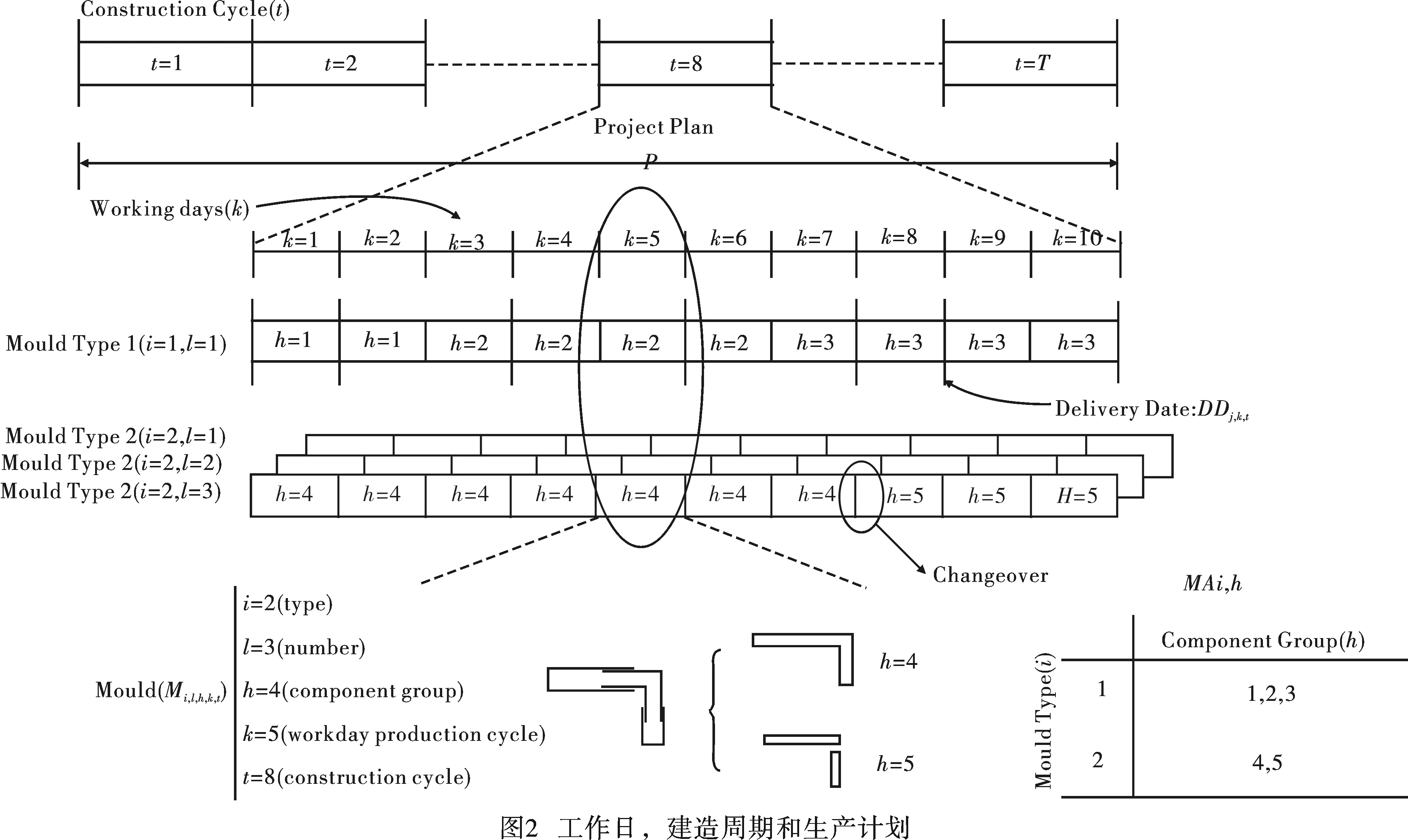
一个建造周期被分割成K个生产和浇筑工作日(k)。生产和浇筑周期定义为单位时间所需完成的所有生产任务，包含模具准备、钢筋绑扎、浇筑、养护、整理加工、运输至生产库存点。假定预制阶段生产和浇筑为一个工作日。

构件厂有一个关于预先设定的截止日期和运输日期需求表，即施工现场在第t个建造周期的第k天所需的j类型构件数，根据安装时间确定的建筑需求表示为DDj,k,t。

模具类型、构件类型和构件分组在生产周期中的关系如图2所示。图2中采用4种模具类型(1个类型1和3个类型2)来生产所有构件。因此，模具类型1的实例l=1,相应的模具2的实例分别为1、2、3(l=1,2,3)。解释下模具适用性矩阵(MAi,h)含义，模具类型2是一个L形模具，既可以生产L形构件也可以生产2个直线型构件，分别称作构件分组4和5。

如果一个模具在相邻的两个生产周期生产不同的构件分组h、h'(h,h'∈H), 那么发生模具切换。例如在图2中，模具2实例3在第7 d生产构件分组4，但在第8 d生产构件5。

为了鼓励模具充分利用它的生产能力,如果模具生产一个构件分组小于它的生产能力，那么引入一个较小的浪费惩罚(Wastcosth)。

每个预制构件的生产包含一系列生产活动任务。假设生产不同类型构件分组的生产能力在时间上是连续的。构件厂生产场地、库存空间有限制，用psl表示。生产商每天的水泥供应量也有限制用csl表示。

此研究对象在于最小化生产商生产成本，通过运用最少的模具类型和数量来满足生产所需的所有建筑构件。在生产寿命周期内最大化利用每个模具的生产能力，提高模具利用率，减少模具浪费，最小化模具切换次数，满足预制构件调装要求。

3 MILP规划模型

3.1 生产计划目标函数

此研究的目标是最小化生产成本。生产成本(TC)包含模具最初预制成本(IMC),模具使用和更换成本(MUC)，模具切换成本(MCC)，模具浪费惩罚成本(NWC)，目标函数为

MinTC=IMC+MUC+MCC+NWC

(1)

(2)

(3)

(4)

(5)

Moldcosti表示模具类型i的建造成本，CHh表示构件分组h的切换成本，wh表示构件分组h的空闲模具指数。

3.2 约束条件

(6)

Mi,l,h,k,t≤MAi,h,i∈I,0≤l≤nl,h∈H,1≤k≤K,1≤t≤T

(7)

Yi,l,h,h',k,t≥Mi,l,h,k,t+Mi,l,h',k+1,t-1,Yi,l,h,h',k,t≤Mi,l,h,k,t，Yi,l,h,h',k,t≤Mi,l,h',k,t

(8)

(9)

(10)

(11)

式(6)表示每套模具的日生产量，式(7)保证每个特定模具分配一个合适的构件分组。式(8)确定一个建造周期的模具切换次数，式(9)表示预制场的空间限制，式(10)表示每天生产构件所需物料小于每日供应量，式(11)表示生产厂满足现场装配计划要求。

4 案 例

以某10层住宅楼为例，建设周期T=5,K=10。该项目的生产区域限制在500 m2,混凝土生产和供应量在每天150 m3，模具的生产使用寿命假定为100次。

该模型由3个方案组成。方案1生产复杂预制结构构件，且允许模具生产构件分组。方案2生产复杂预制结构构件，但不允许模具生产构件分组。方案3采用传统预制方式，作为对比项。

3种方案的结果数据见表1，方案3中传统预制方式生产费用相比方案1高出13.27%,这表示采用复杂模具和构件分组可以明显减少生产费用。方案3中MCC和MWC均为0，这是因为每个模具仅被允许生产专用的建筑构件，所以模具的切换成本和模具浪费惩罚为0。方案1的建造过程中发生模具浪费和切换成本，但通过生产小型构件类型的组合，最大化利用复杂模具。

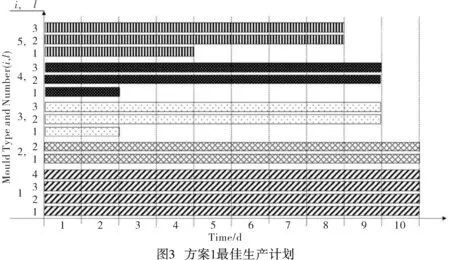
生产计划能从Mi,l,h,k,t中提取，方案1生产计划如图3所示，水平轴表示时间(工作日)，纵坐标表示采用生产构件的模具，水平矩形条表示用使用的模具在对应的时间生产的构件分组。如图3所示，复杂模具类型(i=2)被用来生产3种不同的构件分组(7,8和10)，在一个生产建造周期中只发生4次切换模具，通过应用复杂模具，使用构件分组的思想，促进模具生产一组简单的构件，使模具没有闲置时间。

方案2总费用TC=IMC+MUC=494 800元。尽管模具切换和浪费惩罚为0，但生产总费用比最佳方案1高25.52%，比传统预制方法高10.82%。由方案2的IMC和MUC看出，如果在使用复杂模具时不采用构件分组概念，模具使用率将会很低。综上，不使用构件分组的复杂模具生产方式相比传统预制方法成本更高，使用复杂模具必须和构件分组的思想紧密结合。

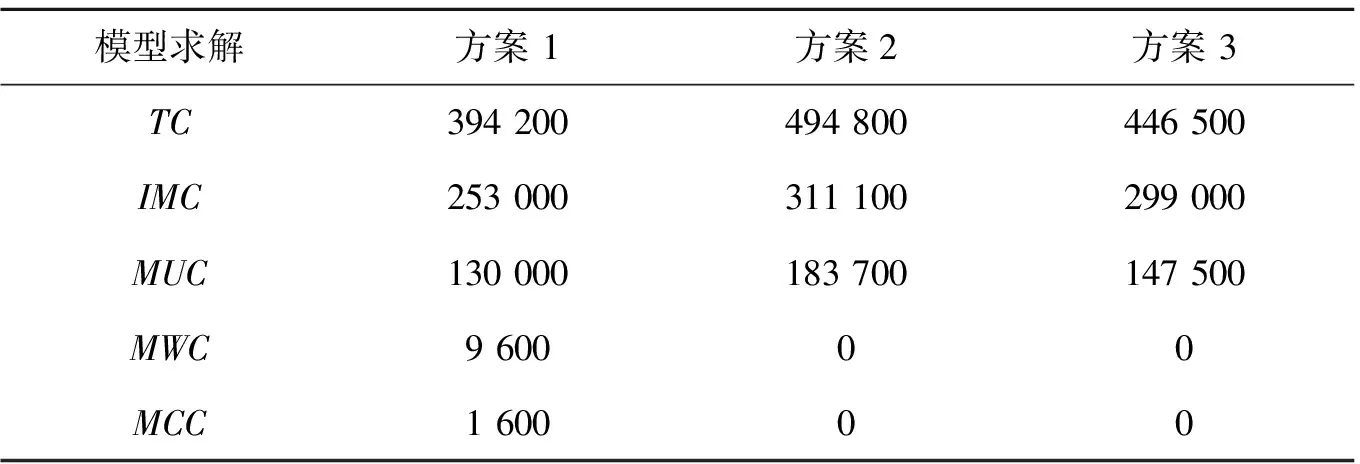
表1 模型计算结果 /元

5 结 论

此研究从设计和生产的角度提出了预制项目规划的解决方案。建立的MILP模型适用于预制生产计划资源和活动的编排，如模具分配、生产排产和交付，并给出在规划范围内所需模具的确切数量和每个模具的时间表。相比传统的预制生产方式，此模型的优势在于：

a.此研究通过引入构件分组的思想，预制构件并非传统建筑元素，而是更复杂的结构构件和模块化单元，有效提高生产率、简化施工。运用新的生产策略达到标准化规模和经济规模，实现复杂模具的充分利用。

b.此模型以建筑构件全生命周期的角度对生产资源进行优化，综合考虑材料供应、场地、吊装需求等限制因素，更具实操性。

c.除了较低的初始模具制造和模具利用成本外，采用复杂模具和构件分组还有其他潜在的好处，比如更少的工人，以及较小的生产区域，减少间接成本。

[1] 王广明.装配式混凝土建筑增量成本分析及对策研究[J].建筑经济，2017(38)：15-21.

[2] 熊燕华，沈厚才，周 晶,等.工程项目调度技术研究综述[J].数学的实践与认识，2013(21)：1-14.

[3] 陈 伟，容思思.装配式住宅项目多空间鲁棒性调度研究[J].建筑经济，2017(38)：69-73.

[4] Girmscheid G,Scheublin F. New Perspective in Industrialisation in Construction: A Atate-of-the-art Report[M].Switzerland:CIB,2010.