基于两种准则下降强法的边坡稳定性对比分析

杨杰

（塔里木河流域喀什管理局，新疆莎车 844700）

1 概述

目前，用于边坡开挖处理稳定性分析准则主要分有Mohr Coulomb（MC）准则和Drucker Prager（DP）准则[1-4]。MC准则既能反映土体不同的抗压强度，还能反应对静水压力的敏感性，且土体参数可通过常规试验测定。而DP准则也在数值计算中得到广泛运用，但如果该准则的参数选取不当，可能导致预测与试验结果之间不一致。对此，有关学者在计算时一般没有指出采用哪种准则进行计算，事实上，采用准则不同，其计算结果也会不同，选用更合适的准则对工程进行模拟具有重要意义。ABAQUS是一套功能强大的工程模拟的有限元软件，本文借助ABAQUS商业模拟软件，在2种准则下采用降强法对沙洋大碑湾泵站岩质边坡进行了稳定性分析，MC模型可以直接采用密度、弹模、泊松比，摩擦角，粘聚力强度等材料参数直接进行计算，而线性DP模型参数需要根据MC模型材料参数进行转换，MC模型屈服面为正六边形，而DP模型屈服面为圆形。MC屈服准则方程为由式子可知，材料参数为ϕ和c，而线性DP模型屈服面在子午平面上是一条直线，其方程式为F=t-由方程式可知，在ABAQUS中确定DP模型的屈服面材料参数为β和d，对平面应变问题，其关联流动线性MC模型和DP模型间材料转换关系为综合考虑上述2种模型，选用更合适的模型模拟边坡稳定性分析具有重要意义[6-7]。

2 稳定性安全评价方法

岩质边坡开挖后稳定性分析问题的过程可以总结为满足特定边界条件下的静力平衡方程、材料非线性本构关系、变形协调条件和合适的强度准则[7]。在确定的荷载边界条件下求得应力应变场和相应的位移场，其通过降低粘聚力强度等材料参数的不同倍数，得到边坡的总位移分布、水平向位移分布、竖直向位移分布和等效塑性应变等分布规律，以及特征点位置处位移和应变分布随降强倍数的变化规律，分析该岩质边坡开挖后的失稳破坏状态，找出开挖后岩质边坡强度稳定处于极限状态下的材料降强倍数，其称之为该岩质边坡的安全系数，以此评价岩质边坡开挖后的稳定状态。

3 边坡开挖处理工程模型简介

沙洋大碑湾泵站岩质边坡高185 m，经过开挖处理后，边坡呈分段多台阶状。采用ABAQUS/CAE对此岩质高边坡建模，开挖边坡模型高185 m，底宽125 m，向左延伸255 m，向右延伸170 m，向下延伸100 m。对开挖边坡二维模型进行细致化有限元网格划分，网格剖分控制设置只有四边形单元，模型共有3 032个节点、2 915个单元，模型的边界采用法向约束，施加重力荷载。根据前述公式对模型参数进行换算，2种模型计算参数见表1。

4 边坡开挖稳定性分析

假设模型的摩擦角保持38°不变，只降低粘聚力强度（1.0，0.8，0.6，0.4，0.2 MPa），计算开挖边坡的稳定性，根据上述二维计算模型条件，通过长变量输出，可得到边坡的总位移分布、水平向位移分布、竖直向位移分布和等效塑性应变分布图，由于计算结果规律相似，这里只展示摩擦角为38°、粘聚力强度为1.0 MPa工况时的计算结果，其计算结果见图1，2。

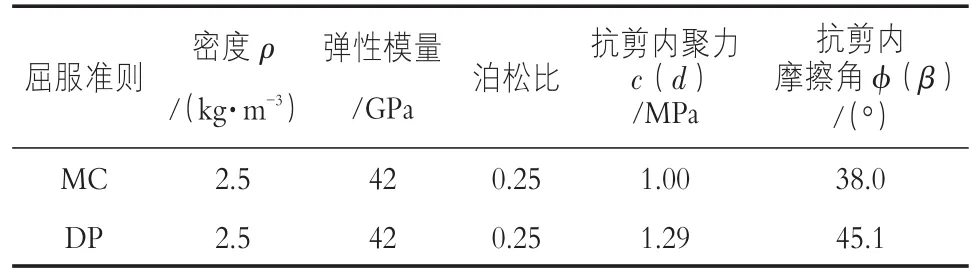
表1 2种模型计算参数表

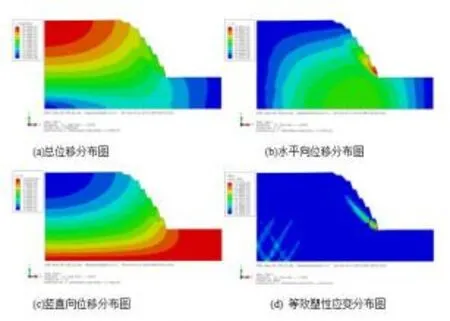
图1 MC模型计算结果图

图2 DP模型计算结果图

由计算结果的水平向和竖直向位移分布图可知，在粘聚力强度大于0.6 MPa时，整个截面的位移是连续光滑分布的，当粘聚力强度小于0.6 MPa时，在边坡附近位移出现突变，这与屈服区滑动面相对应。粘聚力强度c=0.2 MPa时，计算总时步达0.912 8就不收敛，可判断此时边坡失稳。保持粘聚力强度0.2 MPa不变，摩擦角由50°减小到38°，可知，随着摩擦角的减小，屈服区范围逐渐增加，屈服区滑动面倾角变缓。MC模型计算规律与DP模型计算规律相似。

5 结语

采用降强法分析岩质边坡在自重作用下的稳定性，在重力荷载作用下，岩质边坡的破坏属于渐进式破坏，其破坏一般是从坡脚处开始发展，塑性应变慢慢向上延伸，最终边坡坡脚与坡顶的塑性应变形成贯通。对比MC模型和DP模型计算的结果可知，2种模型中边坡的屈服滑动面形态和倾角接近，一般而言，MC模型计算得到的屈服略大于DP模型的结果，当粘聚力为0.2 MPa时，MC模型在基础右侧深处发生较严重屈服，而DP模型在该处则没有发生屈服，这可能是由于MC模型假定破坏与中主应力无关，DP模型的屈服考虑中主应力的影响带来的差异。此外，MC模型屈服面存在转角点，计算收敛性较差，而DP模型屈服面光滑，计算收敛性较好，可为其他边坡开挖处理工程提供借鉴。

［参 考 文 献］

［1］王吉亮，杨静，陈又华，黄孝泉，白伟，魏雨军.复杂层状高陡岩质边坡变形与稳定性研究［J］.水利学报，2015（12）：1414—1422.

［2］刘金，李勤昌，马秀媛.有限元强度折减法在边坡稳定分析中的应用［J］.山东大学学报(工学版)，2016（04）：83—88.

［3］王英，战永亮.关于基坑边坡稳定性计算的思考［J］.水利建设与管理，2003（05）：23-24.

［4］黄强，黄宜胜，肖志勇，陈招军，龚家伟，章朝峰.ANSYS中强度折减法等效DP-MC准则二次开发［J］.人民黄河，2016（04）：94—96.

［5］甄田田，荣传新，程桦，刘小庆.论D-P系列强度准则边坡安全系数的转换本质［J］.科学技术与工程，2016，22：231—234+239.

［6］喻梅，茅献彪，胡新宇.基于ANSYS的强度折减法强度准则转换关系［J］.煤炭技术，2016（09）：123—126.

［7］戴妙林，李同春.基于降强法数值计算的复杂岩质边坡动力稳定性安全评价分析［J］.岩石力学与工程学报，2007（S1）：2749—2754.