基于动态补偿原理的超声波发生器研究
梁杰
(中国电子科技集团公司第二研究所,山西 太原 030024)
在电子行业中,封装形式已逐渐发展为SIP(System In a Package,系统级封装)封装或子系统级封装,零级与一级封装的界限逐渐被模糊化,对半导体后封装工艺及其设备的性能提出了更高的要求。超声引线键合在微电子封装芯片间互联、芯片与外引脚互联有着广泛应用,如功率器件、微波器件、光电器件等的集成电路封装[1]。微系统技术不断发展,除传统的热超声引线键合外,针对多点芯片的热超声倒装键合设备也将广泛应用。超声发生器在键合过程中担负着实现电声转换,产生超声振动,传递超声能量的重任,是超声引线键合机的核心部件[2],如图1所示。它的智能化改进和性能提升会直接推动包括超声键合、超声清洗、超声探伤等多领域专用设备的技术发展。
1 键合过程和影响因素
超声引线键合的连接本质是压力使得引线发生塑性流动导致界面处的元素之间发生原子扩散。超声波一方面使金属引线软化,增强引线塑性流动的能力,另一方面超声波使引线内部产生大量缺陷,成为快速扩散通道,加速了扩散的进行[1]。超声引线键合大致可分为如下几个阶段:
(1)劈刀下降使得引线下表面接触到焊盘后,在劈刀压力的作用下产生初步的受压变形。
(2)超声发生电路产生一个60 kHz的正弦信号驱动换能器,利用反压电效应使得电信号转换为高频的机械振动,再由变幅杆放大振动幅度后传输到需要键合的工作界面上。在键合过程中表现为劈刀和引线相对于静止被键合面的机械摩擦作用。同时,引线吸收一部分超声功率使得自身塑性流动能力增强。引线和焊盘接触面处的氧化膜层在摩擦力的作用下被冲破,接触面受摩擦生热影响温度持续增高,引线塑性变形增强产生更大面积的焊接,焊接强度在元素之间的扩散作用下不断增强。
(3)键合点形成后经历回火阶段,消除残留应力防止变形和开裂,稳定键合点的组织与尺寸。这样就完成了一次键合过程。
完成键合过程的核心阶段在超声源产生的机械振动和功率传递下主导完成。超声的传输效率和控制不仅决定了最终的键合质量,在很大程度上也决定了键合的速度和整机设备的焊接效率。确保超声源、换能系统、劈刀和键合面之间的有效接触和功率匹配是提高键合质量和速度的前提[3,4]。然而,在实际的键合过程中,引线、劈刀、芯片焊盘和基板所组成的界面工况是一个不断改变的动态过程[5]。劈刀、引线和焊盘之间的阻尼及键合面微观特性受多种因素而动态变化,导致系统共振频率,振动浮动和相位的随之而变。反映在劈刀振动上表现为机械振动频率的变化;反映在电路系统上表现为驱动信号频率的变化[5]。如果超声波发生器的频率不变,在加载换能器后,与换能器谐振频率不一致,就会产生失谐,严重时甚至会发生停振[6]。因此,超声波发生器应该具备探测这种系统动态变化的能力,并在一定程度上实时补偿其带来的一系列不良影响。以改善超声键合系统的稳定性和传输效率,从而保证键合工艺的质量和效率。
2 硬件电路实现
FPGA是基于查找表结构的现场可编辑逻辑门阵列,其应用涵盖了逻辑应用、数字信号处理以及嵌入式三大应用领域。选择Xilinx公司Virtex6系列FPGA作为超声波发生器的核心部分。如图2所示,主要完成三个部分的工作:(1)测试部分,作为外设控制核心,应用Verilog语言分别实现各外设芯片的控制核,控制外设AD芯片,DA芯片,SDRAM和USB协议芯片有序协同工作,完成四路参考信号的获取和存储。(2)超声波发生,实现基于DDS(直接数字频率合成)原理的超声波波形发生电路。(3)数字信号处理,利用FPGA的并行高速处理能力结合动态补偿算法完成超声波信号输出的最佳参数寻优和动态补偿。
2.1 测试部分的电路实现
测试部分采集键合设备键合过程中的4个变化量作为数据信号处理的参考信号来源。两个物理量:劈刀压力、劈刀振动频率;两个电信号:换能器输入端的电压和电流信号。劈刀压力和振动频率经过ICP压电传感器和振动传感器(谐振频率在500 kHz以上,响应时间小于1 μs,非线性小于1%FS)后由物理信号转化为电信号。四路电信号经过模拟调理电路的信号调理后成为幅度合适并保留有效特征值的参考信号。参考信号经过A/D芯片采集后成为FPGA可处理的数字信号循环写入SDRAM中4个不同的区块地址中,选择劈刀设定压力的50%作为系统的触发信号。通过负延时字长度的适当设定,在系统被触发后可以完全的保存四路参考信号的动态曲线,后续经过信号调理后输入到FPGA信号处理部分,如图3所示。

图2 超声波发生器原理框图

图3 信号调理电路原理图(单路)
测试部分的电路设计分为模拟信号调理电路和数字采集存储电路。模拟信号调理电路主要完成传感器和系统的电源管理、四路模拟信号与后续数字采集电路的适配;数字采集存储电路主要完成A/D芯片的时序控制(如图4所示),SDRAM芯片的读写时序控制(如图5所示),共同完成四路测试信号的数字化采集和存储。同时数据可通过USB口输出到上位机,可通过上位机软件对测试数据进行直观的观测和分析。
2.2 超声波发生电路的电路实现
超声发生部分采用DDS(直接数字频率合成器)原理实现频率波形的发生,并设计实现了频率控制模块和功率控制模块动态控制波形输出以维持系统的谐振状态。测试部分得到的工况参考信号经过粒子群寻优算法处理后生成控制参数分别传递给频率控制模块和功率控制模块实现测控反馈系统来保证系统输出曲线与负载系统的自匹配。
如图6所示,FCLK代表驱动DDS的时钟频率,K为频率控制字,N位相位累加器由一个累加器和一个N位的地址寄存器组成,ROM中存储2N个输出电平值代表一个周期内对正弦信号的2N个离散抽样值。FCLK驱动累加器以频率控制字K为单位进行累加,累加结果即为ROM sinθ查询表的地址,通过查找表地址输出对应寄存器中的值作为输出电平在FCLK的不断驱动下输出离散波形。累加器加满溢出的时刻对应输出波形的一个周期。通过调整频率控制字K的长度即可调节DDS频率合成器的输出波形频率。频率输出公式即:foutput=K·FCLK/2N,其中FCLK/2N项即为输出频率的分辨率。仿真的波形输出如图7所示。

图4 AD芯片控制流程图
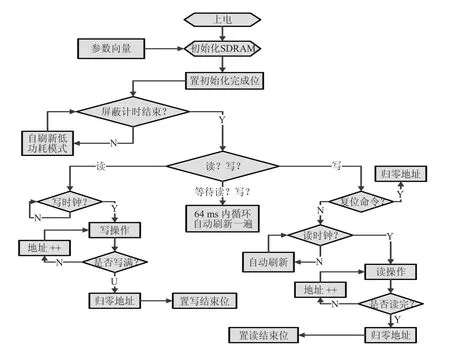
图5 SDRAM芯片控制流程图

图6 DDS频率合成原理图

图7 DDS仿真输出波形图
3 动态补偿原理及实现
常见的动态误差修正方法有数值微分法、叠加积分法、频率域修正法和反卷积法等。目前研究的热点集中在动态补偿技术上,即采取增加补偿环节的办法对系统的动态偏差进行修正。所谓动态补偿即针对动态误差的非线性补偿。动态误差修正技术的目的都是为了提高控制精度,减小动态误差。运用改进PSO算法可得到的最优动态补偿系数按照分布式算法的思想转换成ROM查找表操作,避免了乘法运算,查找表后的数据只需做简单的加法运算就可得到补偿结果,大大提高了运算速度,该方法为动态补偿在线实时测量补偿中的应用提供了一条有效途径[7]。
3.1 建立系统的数学模型
研究系统动态性能的一种方法是对测试系统进行动态校准,根据测试结果进行数据处理,建立全面描述测试系统的动态数学模型,这种方法属于系统辨识法。许多系统的动态特性均可以近似的用低阶系统来描述,其参数的物理意义便见明确,建模方法比较简单实用。
为了获取其动态特性,研究其运动规律。以低阶系统的频率域建模方法建模:
许多系统可以近似用低阶传递函数描述,典型的二阶系统传函为:
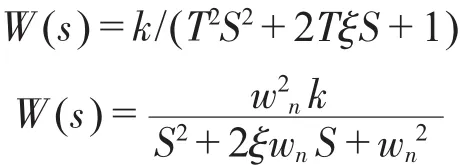
ξ为阻尼比,wn=1/T为系统固有频率
通过实测多个键合过程中四路信号的变化曲线,将得到的曲线样本进行频域变换来得到幅频相应曲线。在有峰值的幅频特性曲线上有5个较重要的特征点:峰值、谐振频率、幅值误差在百分之十内的工作频带、幅度误差在百分之五的工作频带、通频带。得到这些特征点后便可利用峰值与阻尼比的关系求出阻尼比;再用谐振频率与阻尼比求出固有频率;用通频带可以检查回归效果。至此用来描述系统的数学模型就建立了。当然众多更优的方法会得到更加准确的数学模型,这里不做重点研究。
3.2 动态误差的补偿
补偿的基本思路实质上就是:希望补偿模型与实测模型的级联系统输出与理论上的设计频率和功率信号具有最小的动态识差。在补偿时这一目的是通过寻求最佳的模型系数来达到的。因此可将这个问题转化为一个多变量的优化问题。在图8所示的框图中,键合过程对应的系统误差曲线模型经过级联逆模型后得到信号经过寻优算法得到在某参数下的输出曲线与设计值最佳逼近。则我们认为此逆模型即为满足该目标的最佳动态补偿模型。
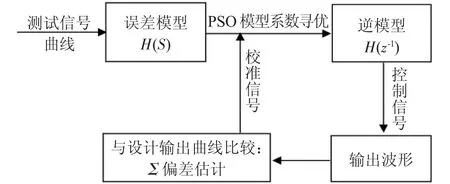
图8 逆模型补偿原理表述图
根据上述思路,容易建立以下目标函数:

ΔT为采样间隔
k为采样点数
逆模型的传递函数为:
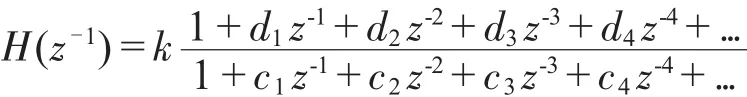
可令 x=(k,c1,c2,...,cn,d1,d2,...,dn)T则模型的设计可描述为求取系数列向量x,使得Σ偏差→0或某设定值Min
由于目标函数F与系数向量x之间没有明确的数学表达式,拟采用一种多变量优化的直接方法一单纯形法:根据问题的维数n选取由n+1个顶点构成。求出这些顶点处的目标函数值并加以比较。确定它们当中有最大值的点及函数值的下降方向,再设法找到一个新的比较好的点替换那个有最大值的点,从而构成新的单纯形。随着这种取代过程的不断进行,新的单纯形将向着极小点收缩。这样经过若干次选代,即可得到满足收敛准则的近似解。利用FPGA的并行处理优势,将乘法运算转换成加法以及移位运算,能够高速完成大量的乘法运算,极大地提高了芯片的使用效率。事先构造一个查找表,该表存储着输入信号二进制表示的每一位所有可能的逻辑值与动态补偿系数与运算的结果,那么就可以通过各个输入变量相应位的组合值来对该表进行查找,从而在摆脱乘法运算的条件下得到计算结果,如图9所示。在进行FPGA实现时,设置一定深度的ROM储存该查找表结构,如图10所示。
动态补偿完成对上一个数据的修正,在FPGA的控制下DA转换芯片将处理结果恢复为模拟信号。最后通过功放电路和匹配电路将模拟信号处理后输出到换能器,构成一套具有动态补偿参数功能的超声波发生系统。

图9 动态补偿并行结构图
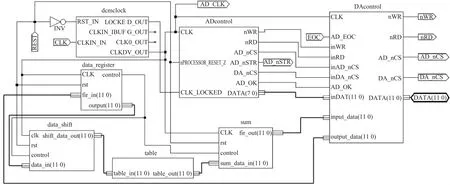
图10 FPGA顶层原理图
4 结束语
本文在对超声键合的工艺过程进行分析的基础上,提出了一种基于动态补偿原理的超声波发生器设计。具体分章节对系统的模拟信号调理电路、数字信号采集存储电路、超声波信号发生电路和动态补偿算法以及其FPGA实现等方面进行了叙述。超声波发生系统通过感知(测试)键合工艺过程中实际非理想状态下工况对超声发生系统产生影响的相关参考变量,再经过对其逆模型(补偿模型)的建模和最优补偿参数的寻优,最终实现超声系统自动补偿影响超声系统稳定输出的不良影响。该系统的实现提高了超声发生系统的自适应和自稳定能力。在全自动键合机的实际应用中,由于前道贴片工序带来的不一致性,表面微观状态的差异性导致的复杂工况变化更加使得设备需要具备这种自动调节能力。在全自动超声设备的应用中,具备动态补偿能力的超生发生器会体现出更重要的作用。
参考文献:
[1]计红军.超声楔焊键合物理工程及其规律研究[D].哈尔滨:哈尔滨工业大学,2005.
[2]马生生,孙丽娜,井文丽.热声焊机超声系统的设计和优化[J].电子工业专用设备,2011,40(5):48-51.
[3]谢敬华,李小平,范良志,国蓉.提高引线键合机超声系统性能的若干因素的分析[J].现代电子技术,2003,(3):65-67.
[4]韩为民.键合机中超声波的基本控制原理及方法[J].电子工业专用设备,2003,32(5):21-26.
[5]王富亮,刘少华.超声引线键合过程的信号采集与分析系统[J].中南大学学报,2010,(6):142-147.
[6]杜晓明.基于FPGA的自适应大功率超声信号源的设计[D].镇江:江苏科技大学,2009.
[7]吴健,张志杰,王文廉.传感器动态误差高速并行修正方法及其FPGA实现[J].传感技术学报,2012,25(1):67-69.
[8]Sascha Eichstadt,Alfred Link,Clemens Elster.Dynamic Uncertainty for Compensated Second-Order Systems[J].Sensors,2010,10(8):7621-7631.
[9]陈贵敏,贾建援,韩琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报,2006,40(1):53-56.
[10]Sheng Chen,Bing L.Luk.Digital IIR filter design using particle swarm optimization.Int.J.Modelling[J].Identification and control,2010,9(7):327-335.

