中立时变时滞系统的稳定性与H∞滤波器设计
薛丽娟,张宝琳
(中国计量大学 理学院,浙江 杭州 310018)
时滞作为物理系统的一个固有特性而广泛存在于通信网络、信号传输、锅炉液位控制、化学化工过程以及网络控制等领域中. 它是系统性能降低甚至不稳定的主要因素之一[1].由于很多动力系统存在时滞[2],因此时滞系统一直是控制领域研究的热点.信号在传输过程中不仅存在时滞现象,也会受到内部噪声和外来干扰的影响,导致接收到的测量信号与真实信号有所偏差.为了消除这种偏差,需要对测量信号进行滤波,即对含干扰因素影响的测量信号进行处理,尽可能得到真实信号的最优估计值.因此,滤波在信号处理中具有重要作用.常见的滤波方法主要有卡尔曼滤波和H∞ 滤波.1960年,卡尔曼通过引入状态变量和状态空间的概念提出了卡尔曼滤波[3].卡尔曼滤波是指从测量信号中通过递归算法估计出真实信号的一种滤波方法.它在控制工程、图像处理、电力系统、管理科学、计算机科学等方面都得到了广泛应用.但卡尔曼滤波方法要求所研究的动力系统是适定的而且外部噪声必须是具有静态特性的白噪声,而这些条件在实际应用中有时不能满足,为了打破这种局限性,1989年,Elsayed和Grimble引入H∞ 滤波[4]概念.H∞ 滤波是通过使用测量信号来估计系统状态进而设计稳定的滤波器且使得从干扰输入到估计误差输出的H∞ 范数小于某一给定的值的一种滤波方法. 与卡尔曼滤波相比,一方面,H∞ 滤波不必获取系统外部噪声的特性,也不要求精确的数学模型,只要求系统的扰动有界即可;另一方面,H∞ 滤波使得估计精度大大提高,从而很大程度上提高了系统的性能.在过去的二十年中,H∞ 滤波在离散Markovian 跳变时滞系统[5]、连续和离散的线性时滞系统[6-10]、模糊系统[11-12]和不确定时滞系统[13-17]等系统中得到了深入研究.另外,文献[18]在线性时变时滞系统中提出了一种新的积分不等式,对Lyapunov导函数中出现的积分项进行进一步研究,从而获得了系统渐近稳定的更大时滞上界,降低了保守性.文献[19]使用交互式凸组合法研究了混合时滞(分布时滞和离散时滞)不确定中立系统的稳定性.对Lyapunov导函数使用交互式凸组合方法,给出了线性矩阵不等式形式的系统鲁棒稳定性判据.文献[20]研究了线性中立时不变时滞系统的H∞ 滤波问题.设计了一个Luenberger 观测器型的H∞ 滤波器,给出了滤波器存在的一个充分条件.但文献[20]研究的系统是时不变时滞的,而在实际工程中,许多物理过程是时变时滞的.因此本文将文献[20]的思想拓展到时变时滞系统中来,设计含有时变时滞环节的H∞ 滤波器.
本文研究一类线性中立时变时滞系统的H∞ 滤波问题.首先,给出了一个新的Lyapunov泛函,采用积分不等式方法[18]和交互式凸组合法[19],得到了中立时滞系统的更低保守性时滞相关稳定性条件.进而,给出了含有中立时变时滞环节的Luenberger 观测型H∞ 滤波器的设计方法.数值例子表明,本文得到了比文献[18]具有更小保守性的结果.同时,所设计的中立时变时滞系统H∞ 滤波器是可行的,有效的.
在文中,“-1”和“T”分别表示求矩阵的逆与矩阵的转置;Rn表示n-维欧几里得空间;Rn×m是所有n×m实矩阵的集合;P>0表示矩阵P是对称且正定的矩阵;“*”表示对称矩阵中的对称项;I是单位矩阵;0是零矩阵.
1 问题描述
考虑如下形式的时变时滞中立系统:

设计如下形式的滤波器:

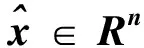
令
进而,由式(1)和式(2)可得滤波误差系统:
其中
(4)
本文研究中立时变时滞系统(1)的H∞ 滤波器设计问题.通过设计滤波器参数K,使得滤波误差系统(3)满足:
条件1.当ωt=0时,滤波误差系统(3)渐近稳定;
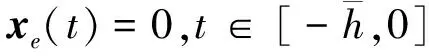
为分析误差系统的稳定性,先给出下面两个引理.
引理1[18]:如果对于任意对称正定矩阵S∈Rn×n,常量a 其中 引理2[20]:如果对于任意对称正定矩阵M∈Rn×n,常量r1 为得到本文的主要结果,先给出下面一组记号: 及 其中 Ψ1-Z≥0. (10) 则滤波系统(3)是渐近稳定的,其中 上式中,Ψ,Θ和P3为: 其中 证明:当ω(t)=0时,误差系统(3)可写为 构造如下形式的Lyapunov泛函: (13) 其中 (14) (15) (16) (17) 令 (18) V(t,xet)沿系统(3)关于时间t求导,得 (19) 其中 (20) (21) (22) (23) 其中,Q=diag{Q1,0,-Q1,Q2,0,-Q2,0}. 根据引理1,得 -ζT(t)Ω1(t)ζ(t)-Ω2(t). (24) (25) 其中, χ1(t)=col{φ1(t),φ2(t),φ3(t)}; χ2(t)=col{φ4(t),φ5(t),φ6(t)}. 令 ζ1(t)=col{χ1(t),χ2(t)}. 对式 (24)、(25)分别使用交互式凸组合方法[19]可得 进而,我们有 (26) 根据引理2,得 (27) 于是,由式(20)至式(27),得 (28) (29) 其中 令 N=N1N2N3N4N5N6N7. 其中,N6和N7为n×n矩阵. 当ω(t)=0时,滤波误差系统(3)可写为: 2ζT(t)NT[A0K-IA1KF000]ζ(t)=0. (30) 于是,由式(28)至式(30)式可得 (31) (32) 其中 式中, h(t)ρ4(t),h(t)ρ5(t),h(t)ρ6(t)}; 令 及 其中,ei(i=1,2,…,12)表示维数为12n×12n的单位矩阵的第i行向量. 则系统(3)是渐近稳定的,其中 (37) 式中, (38) (40) (41) 证明:令 那么 (42) 由引理1,可得 (43) 由引理2,可得 (44) 于是,由(42)至(44),得 (45) 定理3:对于给定的h>0,γ>0,如果存在3n×3n矩阵P>0,n×n矩阵R1>0,R2>0,Q1>0,Q2>0以及n×n矩阵S1和合适维数的W,X使得下列矩阵不等式成立: (46) (47) (48) 其中, 其中,Λ=WTB-XD, Φ14=P12+WTF,Φ24=WTF, Φ23=P12+WTA1-XC1-W, Φ34=P22+WTF,Φ44=Q2. K=W-TX. (49) 证明:选取与式(13)相同的Lyapunov泛函,令 η(t)=col{ζ(t),ω(t)}. 此时,滤波误差系统(3)可写为: 2ηT(t)ΔWΔKη(t)=0. (50) 其中 ΔW=col{WT,WT,WT,0,0,0,0,0}; ΔK=A0K-IA1KF000BK. 令 X=WTK. (51) 由(48)得 (52) 对式(52)两侧同时从0到∞对t积分可得 ≤V(t,xet)t = 0-V(t,xet)t→∞. 因为零初始状态下V(t,xet)t = 0= 0,得 进而得 定理证毕. 为了求出具有更低保守性稳定性准则的滤波器,令 h(t)8,h(t)9,h(t)10}; (55) 其中, 式中, 且 (59) K=W-TX. (60) 证明:令 于是,我们有 (61) 由引理1可得 (62) 由引理2得 (63) 由(3)式得 (64) 其中 令 X=WTK. (65) (66) 并将式(4)、(65)带入式(66)中,得式(59). 由式(59)、(61)至(66),得 (67) 易知,若(56)式成立,则滤波误差系统(3)当ω(t)=0时渐近稳定.另一方面,注意到 定理证毕. 为了验证本文方法的有效性,给出了两个算例. 例1.系统(1) 中,令[18]: 表1 d=-d1=d2取值不同时,使系统渐近稳定的时滞h(t)的最大上界 例2.考虑系统(1),系统参数如下: γhH∞13.1150[-0.11570.1951]T0.52.4201[-0.36730.5557]T0.32.1390[-0.49500.9680]T0.22.1379-0.50000.1000[]T 图1 系统的的状态响应曲线Figure 1 State response curve of system 图2 滤波误差曲线Figure 2 Filter Error curve 本文研究了一类中立时变时滞系统的稳定性和H∞滤波器设计问题.通过构建一个新的Lyapunov泛函,基于新的积分不等式和交互式凸组合法,得到了中立时变时滞系统稳定性的一个充分性条件,并给出了中立时变时滞系统H∞滤波器的设计方法.仿真实例表明本文提出的方法优于文献[18],可以得到具有更小保守性的结果;同时,所设计的中立时变时滞系统H∞滤波器是可行的,有效的. 【参考文献】 [1]NICULESCU S I.Delayeffectsonstability:Arobustcontrolapproach[M].Berlin: Springer,2001:24-30. [2]刘与嘉,张宝琳.含控制时滞的海洋平台前馈反馈最优跟踪控制[J].中国计量学院学报,2014,25(1):99-106. LIU Y J, ZHANG B L. Feed forward and feedback optimal tracking control for offshore steel jacket platforms with control delay [J].JournalofChinaUniversityofMetrology,2014,25(1):99-106. [3]KALMAN R E. A new approach to linear filtering and prediction problem [J].TransactionsoftheASMESeriesD:JournalofBasicEngineering, 1960,82(1):35-45. [4]ELASYED A, GRIMBLE M J. A new approach to theH∞ design of optimal digital linear filter [J].IMAJournalofMathematicalControlandInformation,1989,6(2):233-251. [5]DONG H, WANG Z, HO D W C, et al. Robust H∞ filtering for Markovian jump systems with randomly occurring nonlinearities and sensor saturation:The finite-horizon case [J].IEEETransactionsonSignalProcessing,2011,59(7):3048-3057. [6]DE SOUZA C E,PALHARES R M,PERES P L. Robust H∞ filter design for uncertain linear systems with multiple time-varying state delays [J].IEEETransactionsonSignalProcessing,2001, 49(3):569-576. [7]HUNG Y S,YANG F W. Robust H∞ filter with error variance constraints for discrete time-varying systems with uncertainty [J].Automatica,2003, 39(7): 1185-1194. [8]CHEN N, GU W H, ZHANG X F. Delay-dependent decentralized systems [J].JournalofSystemsEngineeringandElectronics,2008,19(4):766-774. [9]PARK J H. Design of robust H∞ filter for a class of neutral systems:LMI optimization approach [J].MathematicsandComputersinSimulation,2005, 70(2):99-109. [10]FRIDMAN E,SHAKED U. A new H∞ filter design for linear time-delay systems [J].IEEETransactionssignalProcessing,2001,49(11):2839- 2843. [11]CHANG X H,YANG G H. Nonfragile H∞ filtering of continuous time fuzzy systems [J].IEEETransactionsonSignalProcessing,2011,59(4): 1528-1538. [12]ZHANG X M,HAN Q L. A less conservative method for designing H∞ filtering for linear time-delay systems [J].InternationalJournalofRobustandNonlinearControl,2009,19(12):1376-1396. [13]BRIAT C,SENAME O,LAFAY J F. H∞ filtering of uncertain LPV systems with time-delays[C]//EuropeanControlConference. Hungary: Budapest. 2009:2622-2627. [14]GEROMEL J C, BERNUSSOU J, GARCIA G, et al. H2 and H∞ robust filtering for discrete-time linear systems[J].SIAMJournalonControlandOptimization,1999,38(5):1353-1368. [15]TUAN H, APKARIAN P, NGUYEN T. Robust and reduced-order filtering: New LMI-based characterizations and methods[J].IEEETransactionsonSignalProcessing,2001,49(12): 2875-2984. [16]ZHANG H, CHEN Q, YAN H, et al. Robust H∞ filtering for switched stochastic system with missing measurements[J].IEEETransactionsonSignalProcessing,2009,57(9):3466-3474. [17]ZHANG X M, HAN Q L. Robust H∞ filtering for a class of uncertain linear systems with time-varying delay [J].Automatica,2008,44(1):157-166. [18]ZHANG X M, HAN Q L. On tighter estimation of the time derivative of Lyapunov-Krasovskii functional and stability criteria for time-delay systems [J].IEEE,2016,345(47):6806-6811. [19]PARK P, KO J W, JEONG J W. Reciprocally convex approach to stability of systems with time-varying delays [J].Automatic,2011,47(1):235-238. [20]ZHANG X M, HAN Q L. Stability analysis and H∞ filtering for delay differential systems of neutral type [J].IETControlTheoryandApplications,2007, 1(3):749-755.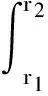

2 主要结果
2.1 滤波误差系统的稳定性分析
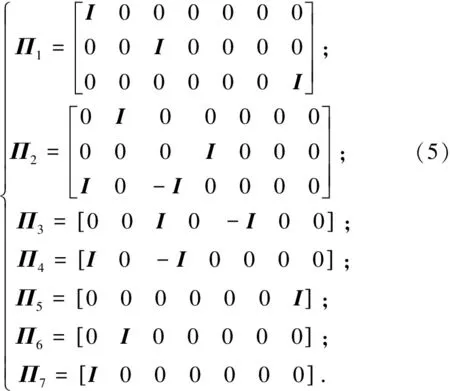

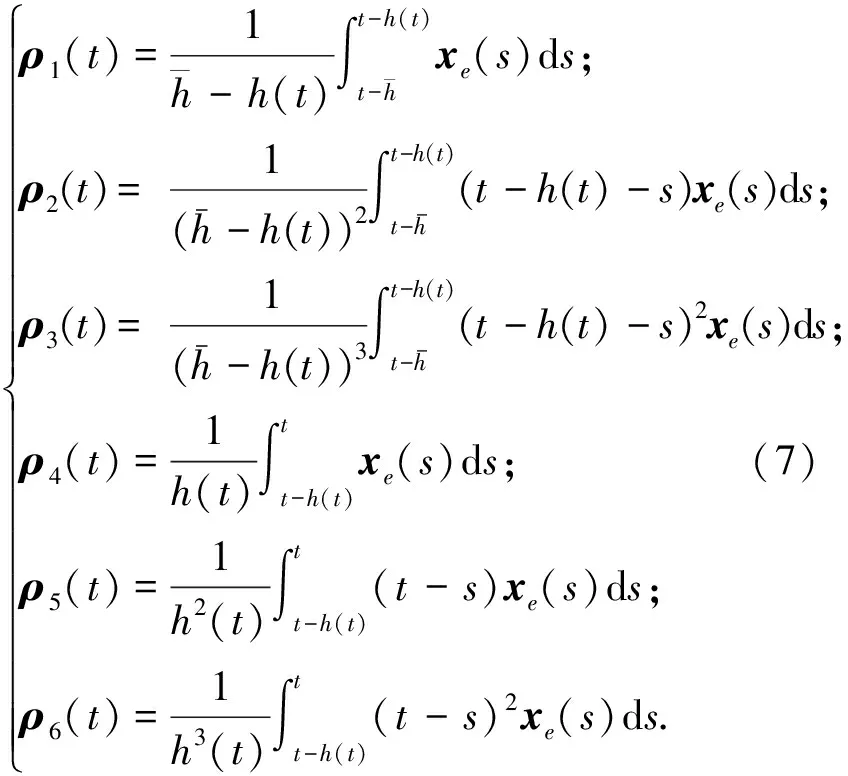


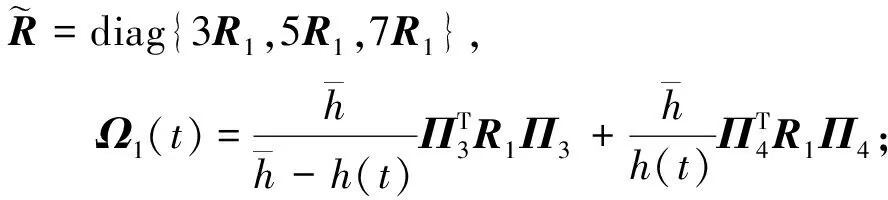
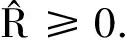
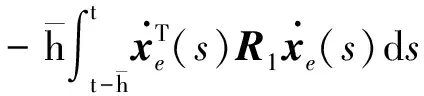
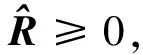
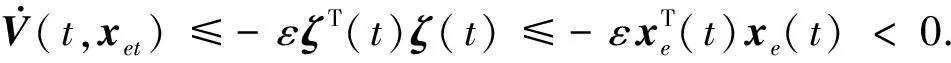

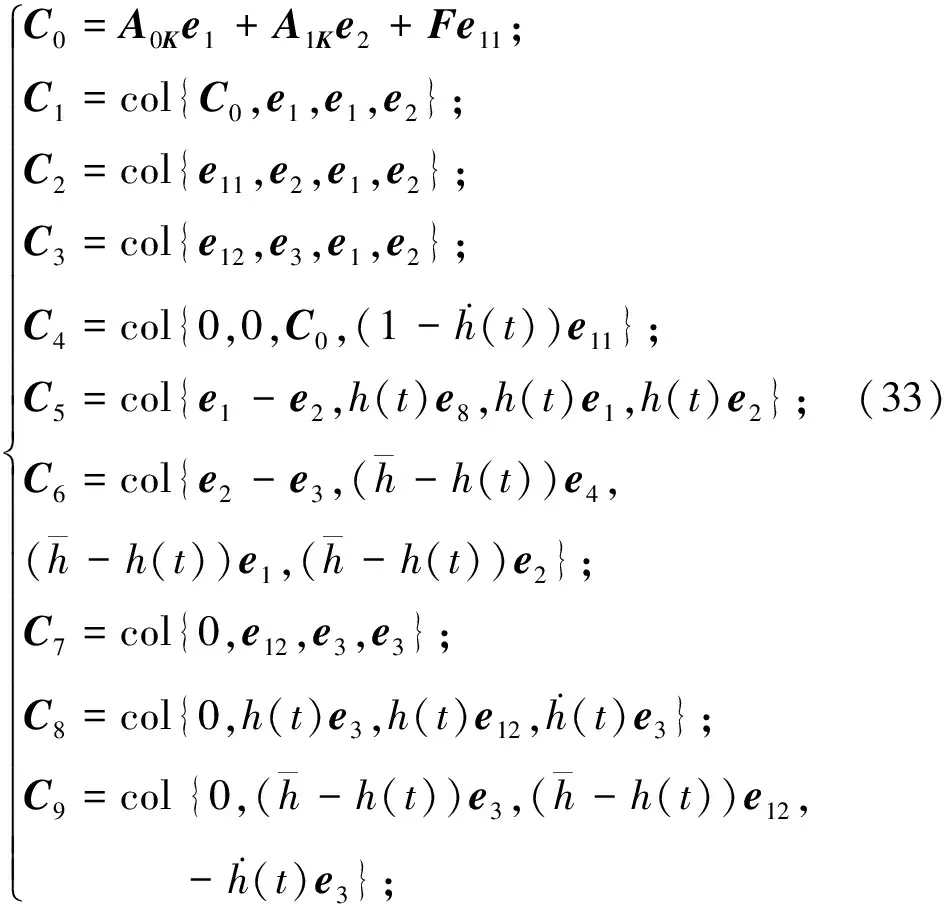

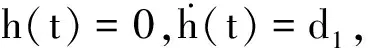
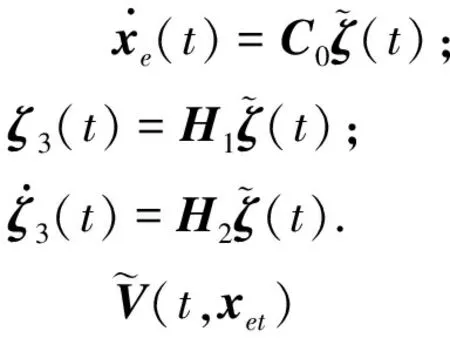

2.2 滤波器设计
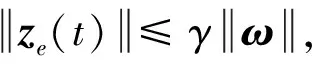

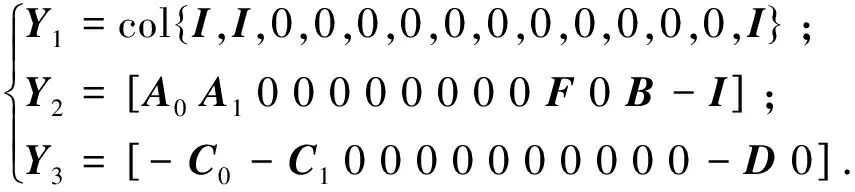
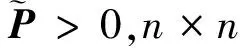
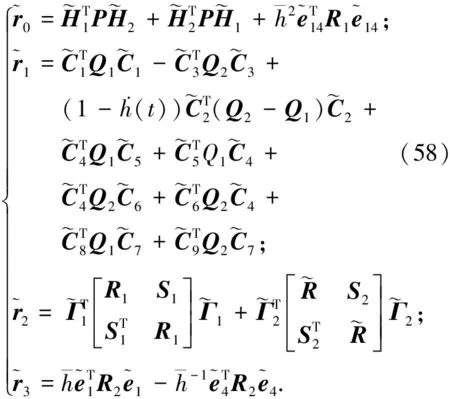
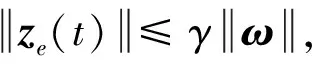
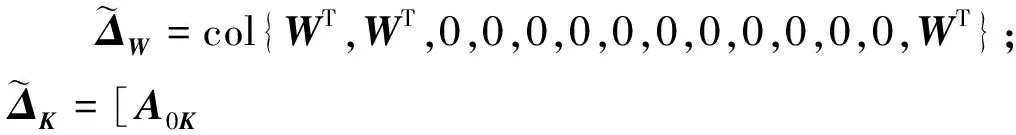
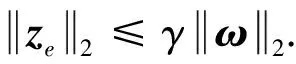
3 仿真实例

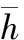

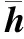
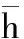



4 结 语

