用于机器人末端残余振动控制的控制误差优化输入整形器
张铁, 林康宇, 邹焱飚, 刘晓刚
(1.华南理工大学机械与汽车工程学院, 510641, 广州;2.桂林航天工业学院广西高校机器人与焊接重点实验室, 541004, 广西桂林)
在工业生产线上的自动化装配、搬运过程中,往往要求机器人末端执行器具备较强的快速定位能力,但是工业机器人中柔性部件的存在导致末端执行器在机器人运动停止后会出现长时间的残余振动,如图1所示,这一现象在机器人高速运动的情况下更为明显,大幅降低了机器人末端执行器的定位精度与速度,严重影响机器人控制系统的稳定性和可靠性。

(a)谐波减速器 (b)J5轴同步带图1 工业机器人柔性部件
输入整形器是一种有效抑制机器人末端残余振动的前馈控制方法,由于其既不需要改变系统的结构,也不需要复杂的反馈回路和传感器,故在工业上得到了广泛的应用,例如桥式起重机[1]、柔性机器人[2]、高速原子力显微镜扫描单元[3]、微铣削机床[4]、太阳翼[5]等。但是,传统的输入整形器也存在诸多问题,例如脉冲序列的长度会引起系统输出的时滞现象;由于对参考输入做了整形,使得实际输出与参考输入间产生不可避免的控制误差;另外,输入整形器的设计依赖于系统固有频率和阻尼比,因此系统参数的不确定性也会影响输入整形器的振动抑制效果。为解决上述问题,众多学者提出不少输入整形器的优化设计方法。例如针对时滞问题,Singhose等提出多种负脉冲输入整形器的设计方法,大幅减小了脉冲序列长度,缩短了系统响应时滞时间[6];Zhao等通过对期望轨迹进行速度规划,再对其进行输入整形来减少时滞时间[7];Kamel等则采用路径规划和输入整形相结合的方法来对系统响应的时滞时间进行补偿[8]。对于控制误差问题,Potter和Robertson等通过构建不同的控制误差代价函数,设计出最小延迟输入整形器(MD)、轨迹修正减少输入整形器(RM)[9-10];Han等通过分解系统实际输出表达式来对控制误差代价函数进行重构,设计出一种不需要系统模型且能减少控制误差的输入整形器[11]。对于鲁棒性问题,Singhose通过增加整形器脉冲数或允许一定量的残余振动设计出了零振动一阶微分输入整形器(ZVD)、零振动二阶微分输入整形器(ZVDD)、极不灵敏输入整形器(SI)[6];Pyung结合时变技术设计出时变输入整形器(TVIST)[12];Pereira结合代数非渐进辨识技术设计出自适应输入整形器[13-14]。这些方法均能降低输入整形器对系统参数的敏感度,从而显著提高输入整形器的鲁棒性。综上所述,诸多新颖的优化设计方法在改善输入整形器某一方面的性能取得了良好的效果,但上述优化方法存在一定的缺陷,如负脉冲的引进可能引起超调现象,影响机器人末端定位精度;延长脉冲序列长度虽能提高整形器的鲁棒性,但也带来了更长的时滞时间;自适应输入整形器和TVIST输入整形器则需要精确的系统动力学模型。
为解决输入整形器应用于工业机器人残余振动控制时存在的时滞问题、控制误差问题和鲁棒性问题,本文提出一种基于输入整形技术的控制误差优化输入整形器设计方法,通过构建关于输入整形器参数的线性约束方程组和代价函数,将输入整形器的设计转化为最优化问题进行求解。线性约束方程组由ZVDD输入整形器约束方程和系统时滞时间方程经整形器时间参数离散化后联立组成,使整形器具备一定的鲁棒性且能应用于实际控制系统中。代价函数由带惩罚因子的整形器脉冲幅值惩罚项和控制误差平方积分项构成,用以实现控制误差的最小化。应用于实际系统时采用预测路径规划(信号前移)的方法来进行时滞时间的补偿。
1 输入整形
输入整形器是一种利用系统固有模态参数进行设计、能够抑制机器人末端残余振动的前馈控制方法,其原理是利用参考输入信号f(t)(t∈[tfa,tfb])与输入整形器g(t)做卷积运算得到的整形输入信号c(t)(t∈[tfa,tfb+tn])来驱动系统,只要选择合适的输入整形器参数,在不改变参考信号系统响应稳态值的情况下,当t>tfb+tn时,输入信号c(t)可以完全消除系统输出的残余振动。其控制流程如图2所示。

图2 输入整形流程图
1.1 ZVDD输入整形器的设计
机器人单一旋转关节可以简化为一个二阶线性系统。以单自由度二阶有阻尼系统为研究对象,Singer给出了多脉冲输入整形器的表达式[15]
(1)
式中:n为脉冲数;Ai、ti为第i个脉冲的幅值和作用时间。
以单位脉冲信号δ(t)为输入信号,系统响应为
(2)
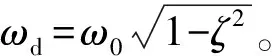
单位脉冲信号δ(t)经整形得到的系统响应为
(3)
当t>tn时,联立式(2)、(3),利用三角函数性质,系统响应可以表示为
Y(t)=A(ω0,ζ)e-ω0ζtsin(ωdt+φ)
(4)
其中
(5)
(6)
(7)
(8)
为消除系统响应残余振动,令A(ω0,ζ)=0,也就是使式(6)、(7)为0,即
(9)
(10)
为了增强输入整形器的鲁棒性,令式(6)、(7)对固有频率ω0的一阶导数、二阶导数均为0,即
(11)
(12)
(13)
(14)
为使整形前后系统输出的稳态值不变,脉冲幅值Ai(i=1,2,…,n)必须满足归一化条件,即
(15)
式(9)~(15)构成一非线性约束方程组,该方程组提供了一种输入整形器的经典求法:令t1=0,对其进行求解即可得到一个ZVDD输入整形器,该输入整形器包含4个脉冲,其表达式如下
(16)

1.2 输入整形器时滞时间的减少和补偿
输入整形器会延长系统响应时滞时间并影响机器人末端执行器定位速度。本文将采用负脉冲和预测路径规划这2种方法来减少和补偿时滞时间。
传统的输入整形器均为正脉冲,但是该条件过于严苛,正脉冲会带来较长的时滞时间,在高速运动下很难实现输入整形,Singhose提出放宽对脉冲幅值的约束条件,允许小幅值负脉冲的存在。该约束的一般形式如下[16]
Aimin≤Ai≤Aimax
(17)
ΔAimin≤ΔAi≤ΔAimax
(18)
式中:Aimin、Aimax为脉冲幅值序列中允许的最小、最大幅值;ΔAimin、ΔAimax为允许的相邻幅值最小、最大增量。考虑到电机性能,式(17)中Aimin与Aimax必须满足条件Aimin≥-1及Aimax≤1,式(18)中ΔAimax取值须满足条件ΔAimax≤2,以保证整形后信号不会引起电机电流过载现象;脉冲幅值序列中的幅值绝对值最大值|Ai|max与相邻幅值最小增量ΔAimin越小,整形后的信号越平滑,但同时也延长了脉冲序列的长度,增加了系统输出的时滞时间,故在此理论基础上需结合实际要求合理选择幅值约束Aimin、Aimax与ΔAimin、ΔAimax。负脉冲可能引起的控制误差问题,将在下一节中通过控制误差代价函数来解决。
预测路径规划是指通过某种方法提前判断输入整形引起的系统响应时滞时间τ,再在整形信号驱动系统前将信号前移τ,从而补偿时滞时间。Kamel给出了斜坡信号整形后的系统响应时滞时间[7]
(19)
延时时间只与输入整形器参数和系统特性有关。若使τ=0并代入非线性方程组进行求解,则不仅可以补偿整形器时滞时间,也补偿了系统特性引起的延时,但是强制性要求延时为0会导致求解出的整形器脉冲幅值过大,造成电机过载。尽管如此,式(19)仍提供了一种判断系统响应时滞时间τ的方法,其具体做法为:先允许存在给定的已知期望系统响应延时τ0,令τ=τ0,代入式(19)做变换得到系统时滞时间方程为
(20)
将式(20)加入非线性约束方程组中重新求解出一个新的输入整形器,使用该整形器所引起的时滞时间即为已知的给定期望时间τ0,这意味着在计算得到输入整形器参数后,不需经过实验即可提前判断其引起的系统响应时滞时间。在确定系统响应的时滞时间为τ0后,将该整形器整形后的信号向前移动τ0再去驱动系统,系统时滞时间即可得到补偿。
1.3 输入整形器的离散化
实际控制系统均为离散时间系统,故传统输入整形器计算出的脉冲时间点及时滞时间τ0可能不是系统控制周期Tc的整倍数,影响输入整形器的振动抑制效果。为解决这一问题,须对输入整形器做离散化处理,使时间参数ti和τ0成为控制周期Tc的整倍数,令
(21)
式中:m为τ0对控制周期Tc的倍数,m∈N。将式(21)代入非线性约束方程组,则可以预先确定脉冲时间ti=(i-1)Tc,故未知量只剩下脉冲幅值Ai,即联立式(9)~(15)、式(20)、式(21),将非线性约束方程组转化为关于脉冲幅值Ai的线性约束方程组
CA=b
(22)
式中:
C=[c1,c2,c3,c4,c5,c6,c7,c8]T∈R8×n
(23)
c1,i=eω0ζ(i-1)Tccos(ωd(i-1)Tc)
(24)
c2,i=eω0ζ(i-1)Tcsin(ωd(i-1)Tc)
(25)
c3,i=1
(26)
c4,i=(i-1)eω0ζ(i-1)Tccos(ωd(i-1)Tc)
(27)
c5,i=(i-1)eω0ζ(i-1)Tcsin(ωd(i-1)Tc)
(28)
c6,i=i-1
(29)
c7,i=(i-1)2eω0ζ(i-1)Tccos(ωd(i-1)Tc)
(30)
c8,i=(i-1)2eω0ζ(i-1)Tcsin(ωd(i-1)Tc)
(31)
A=[A1,A2…An-1,An]T∈Rn
(32)
(33)
式(22)提供了输入整形器设计最优化问题的约束条件,该线性约束方程组可以在抑制系统输出残余振动的基础上使输入整形器具备一定的鲁棒性,并为时滞时间的补偿奠定基础。
2 输入整形控制误差的优化
上一节给出了输入整形器设计最优化问题的约束条件,通过构建合理的代价函数可以设计出符合要求的输入整形器。本节将针对输入整形中存在的控制误差问题,通过构建一个控制误差代价函数以实现控制误差最小化。
以单位阶跃信号为参考输入信号,其二阶系统响应为
(34)
经输入整形后的系统单位阶跃响应为
(35)
设已知系统响应时滞时间τ0,对整形信号做预测路径规划处理,将信号前移mTc,也即等价于将参考信号后移mTc,定义e(t)为实际输出与参考输入间的误差,则
(36)
事实上,可以用有限长时间Tmax代替t→∞这一条件,构建代价函数为
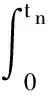
(37)
式中:Q为n×n维正定加权对角阵,Q的对角线元素qi越大,对脉冲幅值向量A的惩罚越大。第2项为过程控制误差项,第3项为定位控制误差项,k1、k2为对第2、3项的惩罚因子。将式(37)各项展开,对第2项有
(38)
令
(39)
对F1、F2项进行化简
(j-1)Tc)dt=ATψA
(40)
式中:ψ为n×n维矩阵,矩阵元素为

(j-1)Tc)dt
(41)
(42)
式中:θ为n维向量,向量元素为

(43)
对式(37)的第3项取Tmax=2tn,有
(44)
令
(45)
对F3、F4项进行化简
(46)
式中:G为n维向量,向量元素为

(47)
(j-1)Tc)dt=ATHA
(48)
式中:H为n×n维矩阵,矩阵元素为

(49)
故代价函数可以表示为
F=ATP1A-2ATP2+k1(n-m-1)Tc+
k2(n-1)Tc
(50)
其中P1=Q+k1ψ+k2H,P2=k1θ+k2G,利用拉格朗日乘子法求解脉冲幅值向量A,构造拉格朗日函数
L(A,λ)=F+λT(CA-b)
(51)
式中:λ为拉格朗日乘子矢量,λ∈R8。L(A,λ)的极值条件为
(52)
解得脉冲幅值向量A的表达式为
(53)
式(53)中矩阵P1不一定可逆,但是当加权正定对角阵Q的对角线元素q和惩罚因子k1满足条件q≥0.2、k1≥1时,可以保证矩阵P1满秩,使幅值向量A有解[8],另外在实际应用中往往对定位误差要求更高,故惩罚因子选择时须满足k2>k1。
选择某个初始脉冲数n0(n0≥8)开始迭代计算,直至解出满足给定幅值约束条件式(17)、(18)的脉冲幅值向量A*,设脉冲幅值向量A*的维数为n,则各脉冲的作用时间ti=(i-1)Tc(i=1,2,…,n),代入式(1)即可得到控制误差优化输入整形器。
3 机器人J5轴末端残余振动抑制实验
为验证本文提出的控制误差优化输入整形器的有效性,本节将从残余振动抑制、过程控制误差、末端定位误差3个方面的实验结果来对控制误差优化输入整形器进行分析,并与ZVDD、CEM输入整形器进行性能比较。在某六自由度机器人J5轴实验平台上进行实验,实验台及控制框图如图3、图4所示。

图3 机器人J5轴实验平台实物图
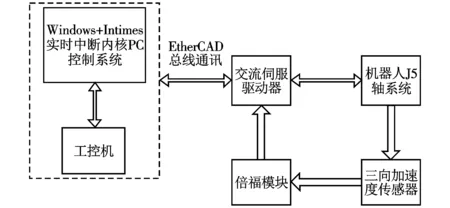
图4 控制系统结构图
系统一阶固有模态参数ω0、ζ可通过模态实验获取;ZVDD输入整形器参数可由式(16)得到;CEM输入整形器参数求解见参考文献[7];控制误差优化输入整形器可利用式(53)进行迭代计算获得,迭代计算所需的参数见表1,为了与ZVDD输入整形器形成对比,表1中的期望系统时滞时间取值为实验测得的ZVDD输入整形器在机器人J5轴上引起的时滞时间τ0。将控制误差优化输入整形器应用于实际控制系统时,由于控制系统为离散时间系统,故对整形信号做前移处理应该为将整形信号向前移动m个点。
以斜坡信号为系统参考输入信号,利用三向加速度传感器检测J5轴末端残余振动加速度,分析整形器的残余振动抑制情况。实验结果如图5所示,
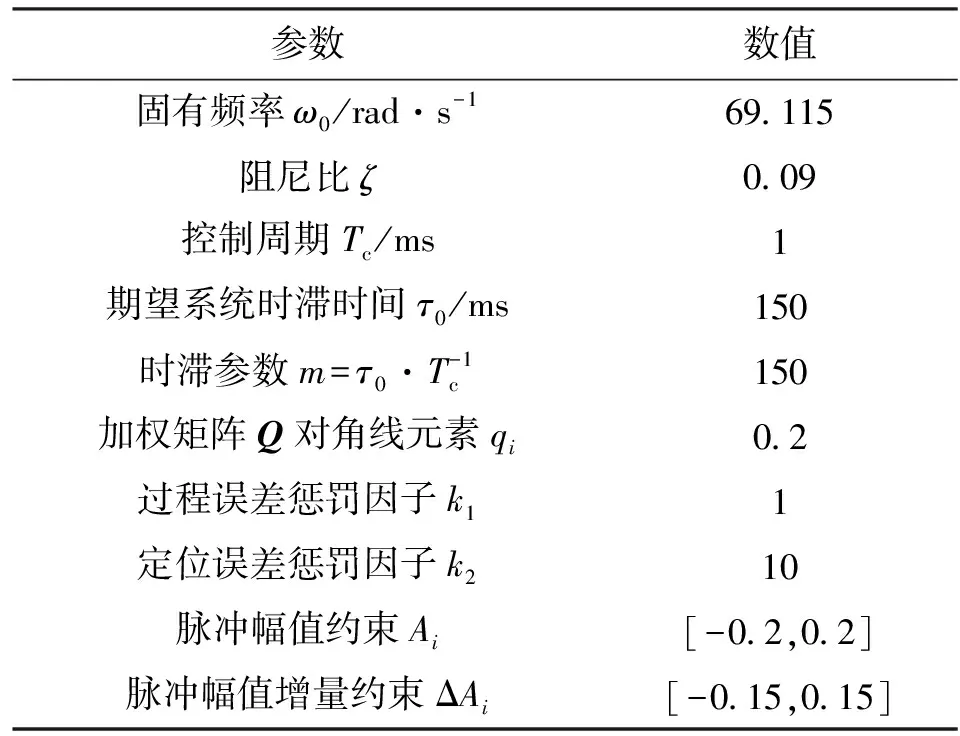
表1 控制误差优化输入整形器计算参数
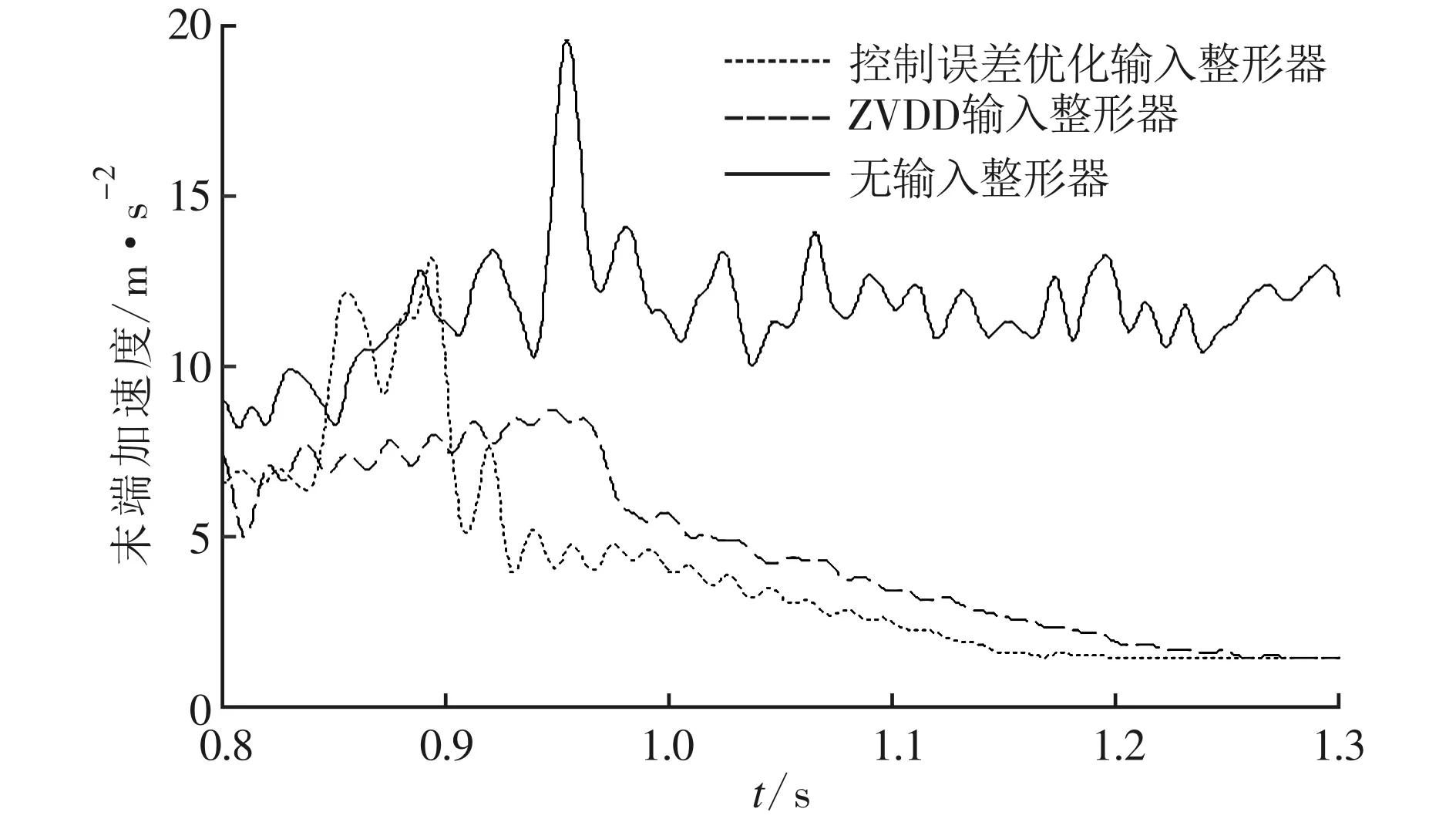
图5 机器人J5轴末端残余振动加速度随时间的变化
在未做整形的情况下,J5轴末端存在长时间的残余振动,其振动加速度约为12 m/s2,当采用控制误差优化输入整形器和ZVDD输入整形器分别对输入信号做整形后,J5轴末端残余振动加速度快速减小并收敛至1.4 m/s2,衰减至未整形残余振动加速度的11.7%,说明这2种输入整形器均能明显抑制末端的残余振动。
采用通过交流伺服驱动器读取到的关节电机编码器脉冲数来对J5轴末段运动轨迹进行研究,分析输入整形器引起的系统时滞时间和控制误差。如图6所示,ZVDD输入整形器引起的系统响应时滞时间τ0=150 ms,而控制误差优化输入整形器由于采用预测路径规划的方法对时滞时间进行了补偿,其引起的时滞时间Δt≈18 ms,与ZVDD输入整形器相比减少了88%。
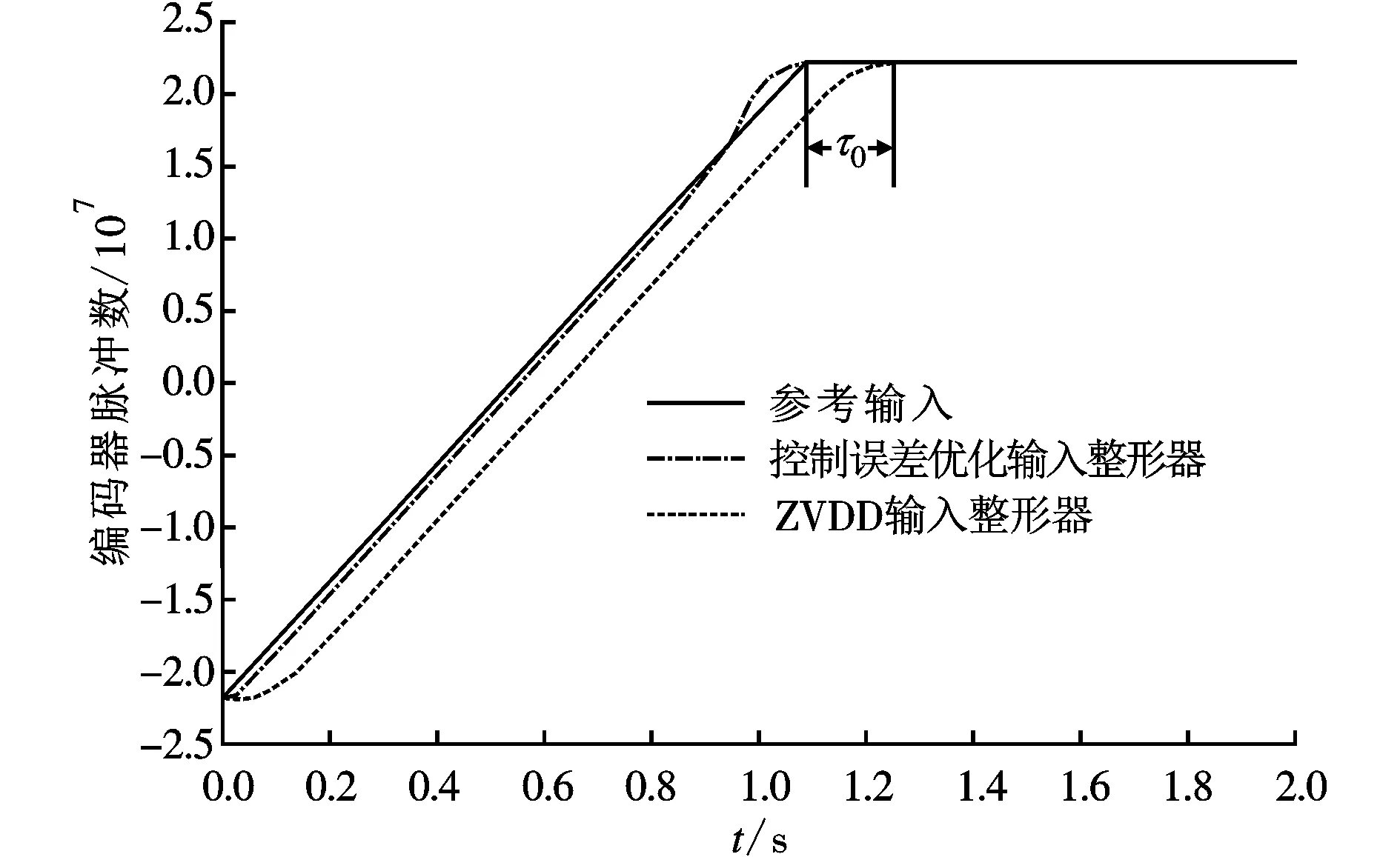
图6 机器人J5轴末端运动轨迹
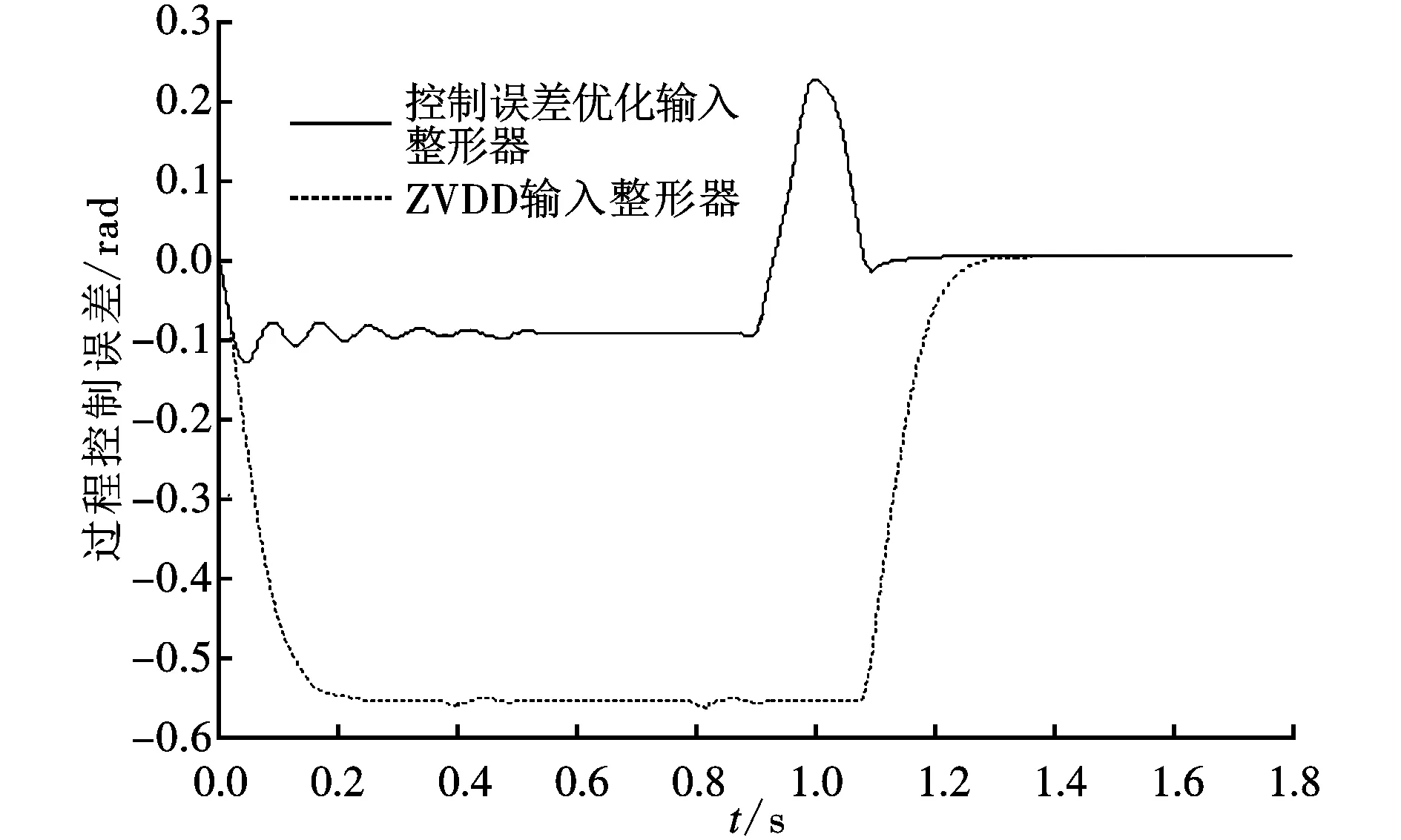
图7 过程控制误差随时间的变化
控制误差优化输入整形器与ZVDD输入整形器的过程控制误差如图7所示,由图可知ZVDD输入整形器的最大过程控制误差|emax|=0.564 rad,其整形后的输出轨迹在J5轴末端运动过程中始终与参考输入间存在一定的控制误差。控制误差优化输入整形器的最大过程控制误差|emax|=0.224 rad,与ZVDD输入整形器相比减小了60.3%,且仅在上升时间的末段出现,大部分上升时间的控制误差|e|=0.095 rad,与ZVDD输入整形器相比减少了83.2%,整形后的输出轨迹与参考输入轨迹基本贴合。

图8 机器人J5轴末端定位误差
输入整形器带来的定位误差如图8所示,控制误差优化输入整形器与CEM输入整形器均对过程误差进行了优化,且为了减少时滞时间,均允许负脉冲的存在。但是,CEM输入整形器并未对负脉冲引起的定位误差进行抑制,其定位误差e=2.71×10-3rad,而控制误差优化输入整形器与ZVDD输入整形器的控制误差基本相同,e=1.28×10-3rad,与CEM输入整形器相比减少了53.7%。由此可见,通过定位误差的优化可以有效减少负脉冲带来的影响,提高定位精度。
4 结 论
针对工业机器人关节柔性引起的末端执行器残余振动抑制问题,提出一种控制误差优化输入整形器的设计方法,通过构建线性约束方程组和控制误差代价函数,解出整形器参数表达式,再进行迭代求解获得控制误差优化输入整形器。在应用于实际控制系统时采用预测路径规划方法对时滞时间进行补偿。实验结果表明,在有效抑制末端残余振动的前提下,控制误差优化输入整形器可以缩短系统时滞时间88%,减小机器人J5轴末端最大过程控制误差60.3%和定位误差53.7%。
参考文献:
[1]MALEKIE. Dynamics and zero vibration input shaping control of a small-scale boom crane [C]∥Proceedings of the 2010 American Control Conference. Piscataway, NJ, USA: IEEE, 2010: 2296-2301.
[2]杨益波. 柔性关节柔性臂杆机械臂动力学建模与振动抑制研究 [D]. 哈尔滨: 哈尔滨工业大学, 2015: 54-57.
[3]SCHITTER G, THURNER P J, HANSMA P K. Design and input-shaping control of a novel scanner for high-speed atomic force microscopy [J]. Mechatronics, 2008, 18(5/6): 282-288.
[4]FORTGANG J, SINGHOSE W, MARQUEZ J D J, et al. Command shaping control for micro-milling operations [J]. International Journal of Control, Automation, and Systems, 2011, 9(6): 1136-1145.
[5]那帅, 朱春艳, 彭福军, 等. 基于输入整形技术的太阳翼调姿残余振动抑制实验研究 [J]. 振动与冲击, 2013, 32(7): 107-112.
NA Shuai, ZHU Chunyan, PENG Fujun, et al. Tests for residual vibration suppression of a solar array during attitude control based on input shaping technique [J]. Journal of Vibration and Shock, 2013, 32(7): 107-112.
[6]SINGHOSE W. Command generation for flexible systems [D]. Massachusetts, MA, USA: MIT, 1997: 99-112.
[7]ZHAO Yu, CHEN Wenjie, TANG Te, et al. Zero time delay input shaping for smooth settling of industrial robots [C]∥Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering. Piscataway, NJ, USA: IEEE, 2016: 620-625.
[8]KAMEL A. New aspects of input shaping control to damp oscillations of a compliant force sensor [C]∥Proceedings of the 2008 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2008: 2629-2635.
[9]POTTER J J, SINGHOSE W. Design and human-in-the-loop testing of reduced-modification input shapers [C]∥Proceedings of the IEEE Transactions on Control Systems Technology. Piscataway, NJ, USA: IEEE, 2016: 1513-1520.
[10] ROBERTSON M, KOZAK K, SINGHOSE W. Computational framework for digital input shapers using linear optimization [J]. Proceedings of the Control Theory and Applications, 2006, 153(3): 314-322.
[11] HAN Jianda, ZHU Zhiqiang, HE Yuqing, et al. A novel input shaping method based on system output [J]. Journal of Sound and Vibration, 2015, 335: 338-349.
[12] PYUNG H C, HYUNG S P. Time-varying input shaping technique applied to vibration reduction of an industrial robot [J]. Control Engineering Practice, 2005, 13(1): 121-130.
[13] PEREIRA E, TRAPERO J R, DIAZ I M, et al. Adaptive input shaping for single-link flexible manipulators using an algebraic identification [J]. Control Engineering Practice, 2012, 20(2): 138-147.
[14] PEREIRA E, TRAPERO J R, DIAZ I M, et al. Adaptive input shaping for manoeuvring flexible structures using an algebraic identification technique [J]. Automatica, 2009, 45(4): 1046-1051.
[15] SINGER N C. Residual vibration reduction in computer controlled machines [D]. Massachusetts, MA, USA: MIT, 1988: 24-39.
[16] SINGHOSE W E, SINGER N, SEERING W. Time-optimal negative input shapers [J]. Journal of Dynamic Systems Measurement and Control, 1997, 119(2): 198-205.
[本刊相关文献链接]
初红霞,谢忠玉,王科俊.一种结合颜色纹理直方图的改进型Camshift目标跟踪算法.2018,52(3):145-152.[doi:10.7652/ xjtuxb201803020]
杨航,刘凌,倪骏康,等.双关节刚性机器人自适应BP神经网络算法.2018,52(1):129-135.[doi:10.7652/xjtuxb201801 019]
朱爱斌,何仁杰,吴玥璇,等.考虑变换域融合方法的刀具磨损区域三维重构.2017,51(12):76-83.[doi:10.7652/xjtuxb 201712012]
蒙雁琦,胡改玲,温琳鹏,等.区域分割的亚像素相位立体匹配算法.2017,51(10):33-38.[doi:10.7652/xjtuxb201710 006]
曹卫权,褚衍杰,李显.针对机器学习中残缺数据的近似补全方法.2017,51(10):142-148.[doi:10.7652/xjtuxb201710 023]
妥吉英,邓兆祥,张河山,等.新型扭转准零刚度的振动角度传感系统.2017,51(8):90-95.[doi:10.7652/xjtuxb201708 015]
张鹏飞,王志恒,席光.用于柔性转子主动控制的等几何Timoshenko梁模型及其数值验证.2016,50(10):139-146.[doi:10.7652/xjtuxb201610021]
刘锦春,何其伟,朱石坚.交叉更新参考信号的振动主动控制方法.2015,49(7):49-54.[doi:10.7652/xjtuxb201507009]
刘石,仲继泽,冯永新,等.使用磁流变阻尼器的大型汽轮发电机定子端部绕组振动控制.2013,47(4):39-43.[doi:10.7652/xjtuxb201304008]
薛晓敏,孙清,伍晓红,等.磁流变阻尼器滞回模型参数的敏感性分析及其简化模型.2013,47(7):102-107.[doi:10.7652/xjtuxb201307019]
马天兵,裘进浩,季宏丽.用于壁板结构多模态振动主动控制的改进最小控制合成(MCS)算法.2012,46(7):87-92.[doi:10.7652/xjtuxb201207016]
郭空明,江俊.采用Kagome夹心板的航天器仪器安装板振动控制.2012,46(7):128-134.[doi:10.7652/xjtuxb201207 023]
薛晓敏,孙清,张陵,等.利用遗传算法的磁流变阻尼器结构含时滞半主动控制.2010,44(9):122-127.[doi:10.7652/xjtuxb201009024]
荆栋,徐晖,王绪伟.内嵌流体欧拉梁减振评价及残余振动衰减分析.2008,42(3):354-358.[doi:10.7652/xjtuxb200803 022]

