带测量误差的分位数回归模型的参数估计研究

关　静，杨香云

(天津大学 数学学院，天津 300354)

一、引 言

在经济、医学、金融等研究领域，预测变量的测量经常带有误差，例如在医学研究脂肪吸收量与乳腺癌患病率之间的关系这一问题中，脂肪的吸收量是无法直接观测的，只能根据脂肪的摄入量来计算。在分析带有测量误差的数据时，如果忽略测量误差所得结果是不可靠的，通常会导致均值回归或者分位数回归的参数估计是有偏的。

关于带测量误差的均值回归，Fuller给出经典最小二乘在忽略测量误差存在的情况下做出的参数估计不再是无偏的，并推导出了偏差的具体形式[1]1-4。为了解决测量误差带来的有偏问题，相关的方法包括：回归递减法[2](修正偏差：Correction Regression)、模拟外推法(SIMEX)[3]、工具变量法(增加工具变量信息)[4]147-150、正交回归法[5]等。

分位数回归用于研究在给定预测变量条件下，响应变量在不同分位数下的分布情况[6-7]。比普通的最小二乘均值回归能够获取更多的关于响应变量的分布信息，可以说传统的最小二乘只是均值的回归，而分位数回归不仅可以反映均值的信息，而且还可以反映分布的上尾和下尾的信息。特别地，实际问题中响应变量与预测变量之间的关系较为复杂，比如当数据出现尖峰或厚尾的分布和存在显著的异方差等情况时，传统的均值回归并不能充分利用数据信息来反映变量之间的真实关系。

本文将测量误差引入分位数回归模型中，重点研究带测量误差的分位数回归模型的参数估计问题。相对于带测量误差的均值回归，这类研究相对很少，因为校正分位数回归中预测变量的测量误差有两大难点[8]：第一，回归误差项以及测量误差项的分布形式未知(若已知可利用似然函数法得到一致估计)；第二，不同于均值回归，随机变量和的期望等于期望之和，而分位数回归中随机变量和的分位数不等于分位数之和。He等提出了正交回归法，通过最小化正交残差的分位数损失函数得到参数估计[9]，该方法要求回归误差与测量误差服从球形对称分布；Hu等提出了基于条件密度函数的非参数模型对参数进行估计[10]；Wei等提出了通过对整个分位数过程进行建模估计给定x条件下y的密度函数，从而用迭代的方法得到参数估计[11]，但计算量庞大且过于复杂；Wang等提出带测量误差分位数回归的校正损失估计[8]；Jiang提出的复合分位数回归方法[12]与Shim提出的加权正交回归的估计方法[13]，同样假设误差服从球形对称分布；Yang等对带测量误差的中位数回归提出随机加权估计，为带测量误差的分位数估计提供了可选的思路[14]，但是同样受限于误差服从球形对称分布。

本文提出利用修正因子得分法解决带有测量误差的分位数回归的参数估计问题：首先，利用因子得分法对预测变量进行估计[15]；其次，利用响应变量y与估计的预测变量做分位数回归，并对估计结果进行修正得到最终估计，即修正因子得分估计；再次，通过随机模拟，比较在不同情形下修正因子得分(CFS)估计与Naive估计(忽略测量误差的估计)以及正交回归(H-L)估计的优劣。

二、模型分析

考虑带测量误差的分位数回归模型：

τ∈(0,1)

(1)

W=X+u

(2)

(3)

得到参数的一致估计,其中ρτ(u)=u(τ-I(u<0)),I(·)为示性函数。Koenker给出了估计方法与相应的性质[16]69-105。当预测变量X带有测量误差时，原有的方法将不再适用，而带有测量误差的均值回归所提出的方法，如回归递减法、模拟外推法、工具变量法、正交回归法等，对于带有测量误差的分位数回归模型也不能直接使用。针对测量误差分位数回归模型，He和Liang提出正交分位数回归模型，并在测量误差与回归误差服从球形对称分布的假设下得到了参数的一致估计。

三、修正因子得分估计

(一)因子得分法

Thoresen和Laake于1999年在研究带测量误差的Logistic回归模型参数估计中，提出了利用因子分析中的因子得分理论通过工具变量信息估计预测变量X，进而估计回归参数的方法[15]。下面在式(2)的基础上引入工具变量：

Z=α0+α1X+δ

(4)

其中Z与X相关，且误差项δ服从正态分布。结合式(2)和式(4)可写成以下形式：

(5)

假设Var(u)=Var(δ)=ψ2，Var(X)=γ2，则有：

(二)修正因子得分法

对于带测量误差的分位数回归模型，本文提出修正因子得分法。利用因子得分法估计预测变量,然后用Y与所估计的预测变量做分位数回归，并对其估计结果进行修正，从而得到参数(β0，β1)的最终估计。

1.将因子得分法在原方法基础上进行改善。在因子得分法中假设测量误差u和工具变量与X的回归误差δ的方差相等，通过添加替代变量W的重复测量信息W1从而去掉该假定，W1满足：

W1=X+u1

(6)

图1　测量误差影响下的中位数估计图

图2　测量误差影响下的75%分位数估计图

四、随机模拟

本文应用R软件对修正因子得分估计法和正交回归估计法进行随机模拟，并对模拟结果进行分析比较。

表1　β0=2　β1=1　ε～N(0，1)　u～N(0，1)　δ～N(0,1)

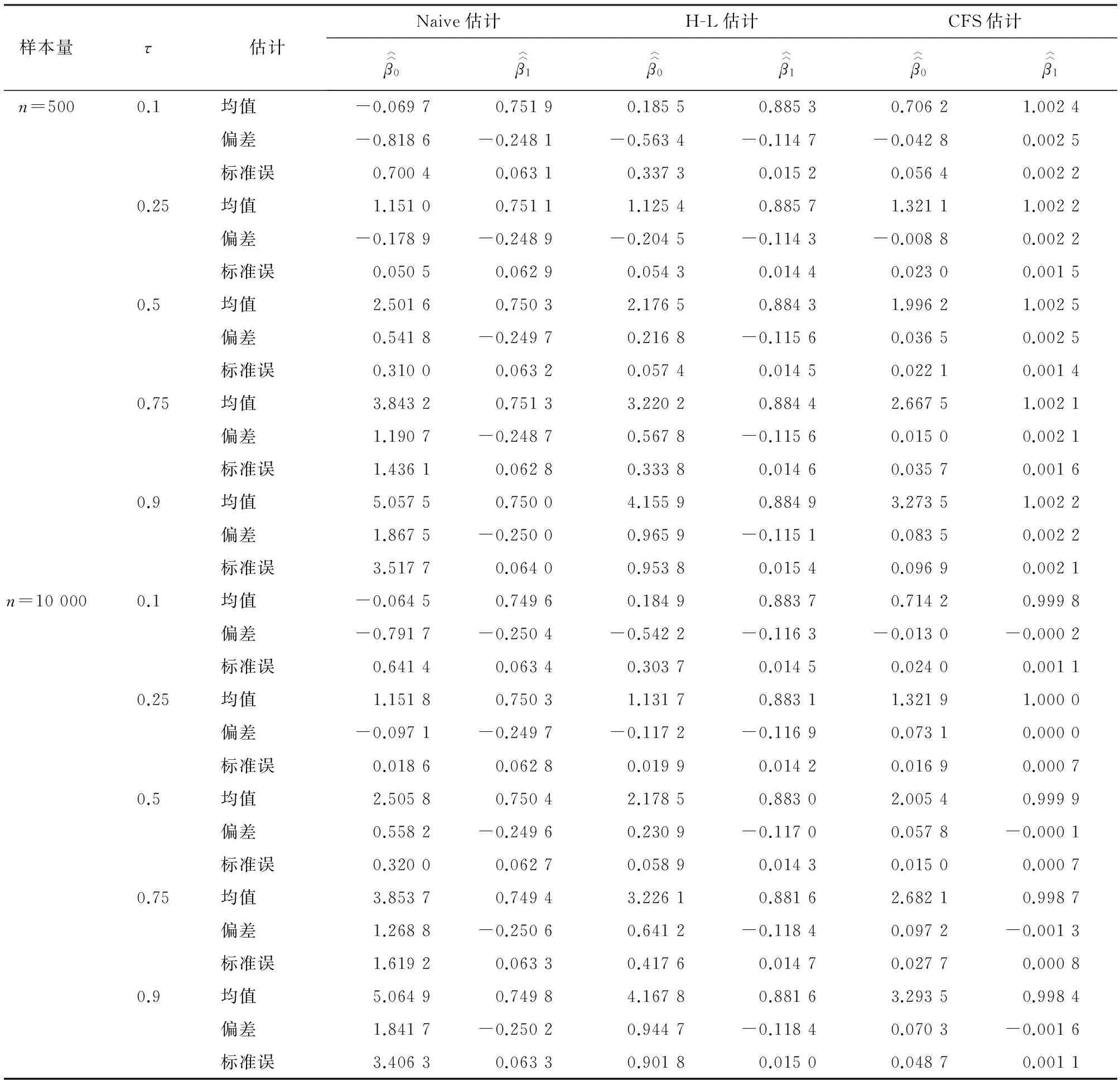
表2　β0=2　β1=1　ε～N(0,1)　u～N(0,2)　δ～N(0,1)

整体来看，在各个分位数水平下，本文所提出的修正因子得分(CFS)估计都有较优的估计效果，并且通过改变样本大小，发现随着样本量的增大估计效果更优，这一点在低分位数和高分位数的截距项的估计结果中尤为明显。

表3　β0=2　β1=1　ε～N(0,2)　u～N(0,1)　δ～N(0,1)

五、总 结

测量误差模型在经济、金融、生物、医学等领域迅速发展，是近年来统计学研究的热点问题之一，而分位数回归模型理论的不断完善也使其受到了广泛应用。因此，本文针对带测量误差分位数回归的参数估计问题展开研究。

在介绍线性测量误差模型的基础上给出测量误差的存在造成的参数估计的偏差，引入分位数回归模型，并给出现有的带测量误差的分位数回归估计方法(正交回归法等)；因子得分法由Thoresen和Laake提出，用于估计预测变量X；本文在此方法的基础上进行了改进，用改进后的方法估计预测变量X，用估计的X与Y回归，并对估计结果进行修正，提出了修正因子得分法。

本文提出的修正因子得分法的优势在于：其一，在使用因子得分法估计预测变量时加入重复测量，克服了需要假设测量误差与工具变量误差方差相等或者等比例的缺陷，放宽了因子得分法的约束条件；其二，只假定回归误差、测量误差、工具变量误差均服从正态分布，对不同误差分布的方差不做其他假定。相对于正交回归法，放宽了约束条件。

模拟结果显示：修正因子得分法比Naive估计有了很大改善，在球形对称分布假设条件下修正因子得分法的估计效果与正交回归法相当，但当回归误差方差与测量误差方差不等的情形下(不满足球形对称分布假设)，修正因子得分法仍然有较好的估计，在估计的平均偏差和标准误等方面表现出良好的性质，而此时正交回归法不再适用。综合来看,修正因子得分法作为带测量误差分位数模型的估计方法具有一定的优良性。

参考文献：

[1]Fuller W A.Measurement Error Model[M].New York：John Wiley，1987.

[2]Wang N,Lin X H,Guttierrez R G.A Bias Correction Regression Calibration Appoach in Generalized Linear Mixed Measurement Error Model[J].Communications in Statistics-Theory and Methods，1999，28(1).

[3]Cook J R，Stefanski L A.Simulation-Extrapolation Estimation in Parametric Measurement Error Models[J].Journal of the American Statistical Association，1994，89.

[4]李子奈,潘文卿.计量经济学[M].北京：高等教育出版社,2010.

[5]Brown M L.Robust Line Estimation with Error in Both Variables[J].Statistical Association，1982，77.

[6]袁晓惠,刘天庆.数据随机缺失下分位数回归模型的诱导光滑估计法[J].统计与信息论坛,2017(6).

[7]李育安.分位数回归及应用简介[J].统计与信息论坛,2006(3).

[8]Wang H J，Stefanski L A，Zhu Z.Corrected-Loss Estimation for QuantLle Regression with Covariate Measurement Errors[J].Biometrika,2012，99(2).

[9]He X，Liang H.Quantile Regression Estimates for a Class of Linear and Partially Linear Errors-in-Variables Models[J].Statist Sinica，2000，10(1).

[10] Hu Y，Schennach S M.Identification and Estimation of Nonclassical Nonlinear Errors-in-Variables Models with Continuous Distributions Using Instruments[J].Econometrica，2008，76.

[11] Wei Y，Carroll R J.Quantile Regression with Measurement Error[J].Journal of the American Statistical Association，2009，104(487).

[12] Jiang R.Composite Quantile Regression for Linear Errors-in-Variables Models[J].Hacettepe Journal of Mathematics and Statistics，2015，44(3).

[13] Shim Jooyong.Quantile Regression with Errors in Variables[J].Journal of the Korean Data and Information Science Sociaty，2014(2).

[14] Yang X H，Jiang R，Qian W M.Randomly Weighted LAD-Estimation for Partially Linear Errors-in-Variables Models[J].Chinese Annals of Mathematics Series B，2015，36(4).

[15] Thoresen M，Laake P.Instrumental Variable Estimation in Logistic Measurement Error Models by Means of Factor Scores[J].Communicationsin Statistics-theory and Methods，1999，28(2).

[16] Koenker R.Quantile Regression[M].New York:Cambridge University Press，2005.