大型天然气压缩机组节能优化软件设计
刘航铭 周元华* 易先中* 徐梦卓 刘 欢
1(长江大学机械工程学院 湖北 荆州 434023) 2(中石化石油机械股份有限公司压缩机分公司 湖北 武汉 430000)
0 引 言
随着我国天然气开采技术的不断提高,国民生产中对天然气的使用量也呈上升趋势,天然气压缩机作为西气东输工程中的重要设备,其功耗及运维成本将直接影响天然气的输送成本。调查表明,在天然气的输送过程中,压缩机组的功耗巨大,其消耗的能量约为管道所输气体能量的3%~5%,因此,针对大型压缩机组的运行优化研究十分必要。
目前国内外许多学者在压缩机优化运行中做了许多的研究工作。Jean Mino[1]通过改进压缩机本身对其进行结构优化,使压缩机达到最大吞吐量;埃及石油研究Elshiekh等[2]通过对压缩机站管道网络中燃料消耗优化,使燃料消耗达到最小化;美国西南研究院Augusto Garcia-Hernandez等[3]分析不同的气体成分对管道和压缩机运行效率及性能的影响;浙江工业大学李颖[4]通过热力学和动力学计算,提出对压缩机本身关键部件及工艺参数进行改造,从而实现压缩机的运行优化。里贾纳大学和saskenergy/transgas公司采用模糊规划模型进行计算,确定压缩机组的开启和关闭[5]。Suming Wu和Mercado等[6]解决了稳态条件下天然气管道压缩机站的燃料成本问题,给出了天然气管网的优化方案。Chebouba等[7]采用蚁群算法对含有压缩机的输气干线进行了优化。MohamadiBaghmolaei等[8]研究了目标函数为输气干线压缩机能耗最低的几种优化方法,优化结果表明人工神经网络起到了最佳的优化效果。Advantica Stone公司和Simone公司、美国TETCO输气管道公司等都进行了输气管网非稳态下优化运行的研究,并且已经在模型和算法上取得了一定的进展[9-10]。可见在输气干线运行优化问题的研究方面取得了突破。
本文经过对比研究上述国内外专家学者的方法及理论,发现针对压缩机本身的优化研究主要是对其自身结构或关键部件进行优化,算法的研究则主要倾向于对压缩机输气干线的优化。本文以某增压站往复式压缩机组运行能耗最低为目标,在保证输气干线输气压力和输气量的条件下,开发压缩机组节能优化软件。采用神经网络计算方法预测压缩机组的进气压力和轴功率,优化压缩机运行工况,合理调配压缩机组的运行组合,进而达到该增压站往复式压缩机组节能降耗的目的。
1 压缩机运行模型
往复式天然气压缩机组作为输气干线的核心装备,其数学模型包含有等式约束和不等式约束,建立压缩机数学模型来预测进气压力和轴功率,对于输气干线优化运行有重要意义。对于不同的压缩机站而言,其含有压缩机的数目和型号也不尽相同,本文以单台压缩机为单位,进行压缩机的能耗优化分析。
根据压缩机理论,往复式压缩机轴功率可以表示为:
(1)
式中:Nz、Ni分别为压缩机轴功率、指示功率,kW;Pcin、Pout分别为压缩机进气压力、排气压力,Pa;Qcin为压缩机进气量,m3/s;ηm为压缩机机械效率;k1、k2是与压缩机性质相关的系数。
压缩机进气量应在一定范围内:
(2)
式中:Qcin、Qcin min、Qcin max分别为压缩机进气量、最小进气量、最大进气量,m3/s;Qout、Qout min、Qout max分别为压缩机排气流量、最小排气流量、最大排气流量,m3/s。
为保证输气、用气安全,进气压力和排气压力限制如下:
(3)
式中:Pcin、Pcin min、Pcin max分别为压缩机进气压力、最小进气压力、最大进气压力,Pa;Pout、Pout min、Pout max分别为压缩机排气压力、最小排气压力、最大排气压力,Pa。
考虑到压缩机的实际工况,压缩机轴功率和转速限制如下:
(4)
式中:Ni、Ni min、Ni max分别为压缩机轴功率、最小轴功率、最大轴功率,kW;nm、nm min、nm max分别为压缩机转速、最小转速、最大转速,r/min。
由此可知,压缩机进气压力、轴功率与进气量、压缩机转速、排气压力、排气流量、气体温度(进气温度和排气温度)等有密切关系。在保证下游输气压力和输气量条件下,即选用最小轴功率和最小进气压力时压缩机组功耗最低。
2 神经网络模型建立与训练
2.1 建立神经网络模型
BP一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小[11]。其中前馈式网络结构特别适用于BP算法,如今已得到了非常广泛的应用。如图1所示。

图1 多层前馈网络典型结构图
在图1中,输入层有m个神经元节点,隐含层有p个神经元节点,输出层有n个神经元节点,wij(i=1,2,…,m;j=1,2,…,p)为输入层到隐含层的权值,vjk(j=1,2,…,p;k=1,2,…,n)为隐含层到输出层的权值,θj(j=1,2,…,p)隐含层阈值,αk(k=1,2,…,n)为输出层阈值,(x1,x2,…,xm)为网络输入向量,(y1,y2,…,yn)为网络输出向量,Yh为期望输出,e为误差。
合理选取影响进气压力和轴功率的主控因素,对准确建立神经网络模型起关键性作用,由式(1)-式(4)可知,压缩机组的进气压力和轴功率与进气量、压缩机转速、排气压力、排气量、进、排气体温度等有密切的关系。因此,将已有的压缩机进气温度、排气压力及所需排气量作为神经网络模型的输入,且确定输入层节点个数有3个。对于隐含层节点的个数没有一个确切的理论方法,需要根据设计者的经验及生产实际来确定,若数目太少,则神经网络所能获取的用以解决问题的信息就会太少;若数目太多,就会增加学习时间,甚至出现“过度吻合”问题,即测试误差增大导致泛化能力下降[12-14]。因此根据经验及实验验证,最终确定隐含层个数为50个。将需要计算得出的进气压力、轴功率及排气温度作为神经网络的输出层,因此输出层节点个数为3个。构建出压缩机组数值预测神经网络模型如图2所示。

图2 压缩机组数值预测神经网络模型
2.2 BP神经网络模型训练及其预测
神经网络模型建立完成之后,通过训练学习才能完成给定的映射关系,为准确预测进气压力和轴功率。本文以“西气东输”中某增压站的大型往复式天然气压缩机组为例(该增压站10台大型往复式增压压缩机,通常采用一运一备的方式进行工作),进行了大量现场测试实验,实际测试过程中,温度数据为:0,4,8,…,20 ℃;吸气压力数据为:1.5,1.8,2.1,…,4.5 MPaG;吸气压力数据为:4.85,5.0,5.2,…,6.0 MPaG,共计采集上述正交实验数据2 046组。其中测试部分数据如表1所示。
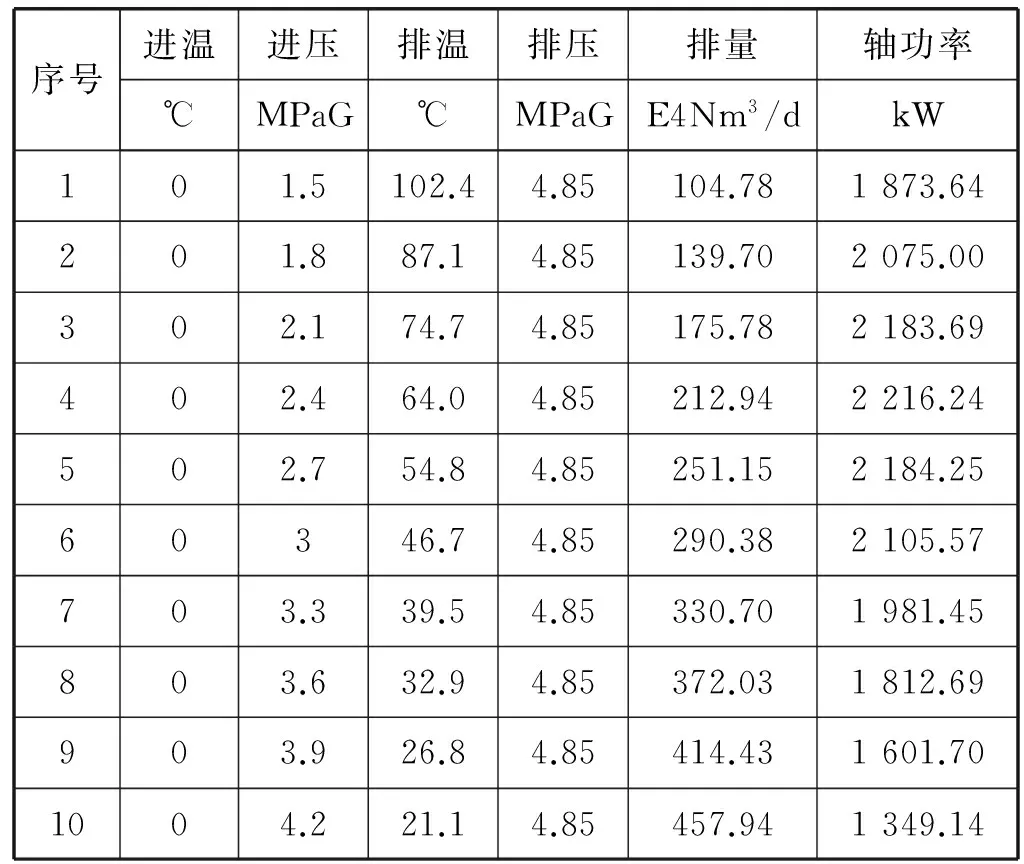
表1 6RDSA-1往复式天然气压缩机部分测试数据
将现场采集的2 046组数据分为训练数据和测试数据,对BP神经网络进行训练与测试,其测试建立的神经网络模型的计算流程如图3所示。
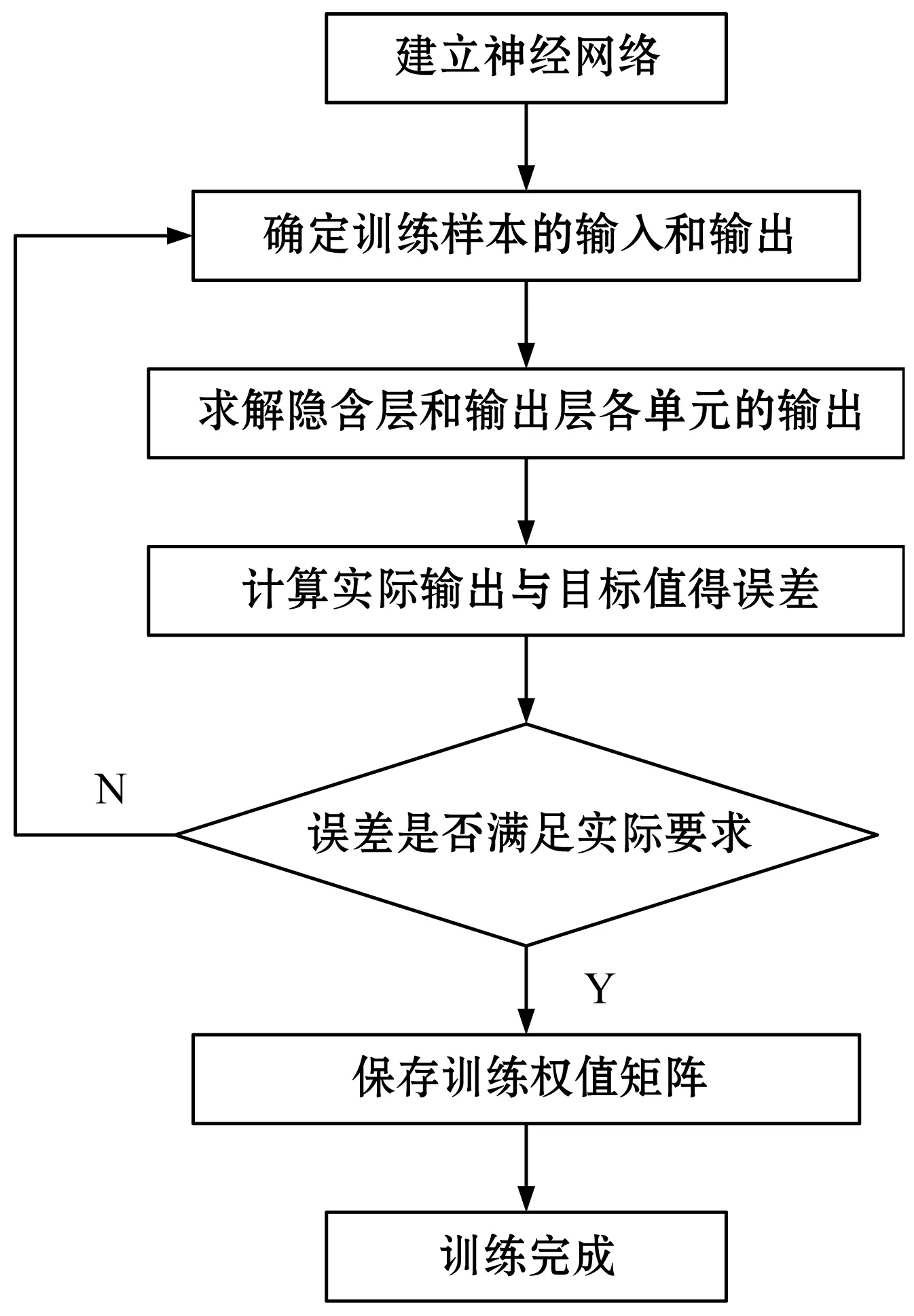
图3 BP神经网络算法计算流程图
在进行模型预测能力评价时选用相对误差作为评价指标,神经网络模型预测结果与实测值的相对误差曲线如图4所示。神经网络模型的测试结果与实测值的对比曲线如图5所示。

图4 神经网络模型预测结果的相对误差

图5 神经网络模型预测结果与实测值对比
经过上述对神经网络模型的训练及测试可知,神经网络模型预测的结果与现场采集的实测值之间的仿真曲线几乎重合,相对误差小于1.8%。
3 压缩机组节能优化软件及现场应用
3.1 压缩机组节能优化软件设计
经过对BP神经网络算法的研究,建立了针对某增压站6RDSA-1型往复式压缩机的数值预测神经网络模型。采用C语言编译软件,提出了基于BP神经网络的进气压力与轴功率预测方法,在Lab Windows/CVI中实现天然气压缩机组节能优化软件开发,软件的输入主界面如图6所示。图6中输入参数栏包括进气温度、排气压力和排气流量三个值,根据现场要求及该型号压缩机安全运行的需要,对所需要输入的参数设定了安全范围,压缩机站现场的工作人员可以根据已知的信息,在相应的区域输入具体值。计算方法栏提供了两种计算数据,在软件没有与压缩机组同步运行时,可以使用理论数据(即前期现场采集的压缩机组实际运行的数据)计算。在软件与压缩机组同步运行时,此时可以使用实测数据(即现场压缩机组运行时地同步数据)计算。计算结果为进气压力、轴功率和排气温度。
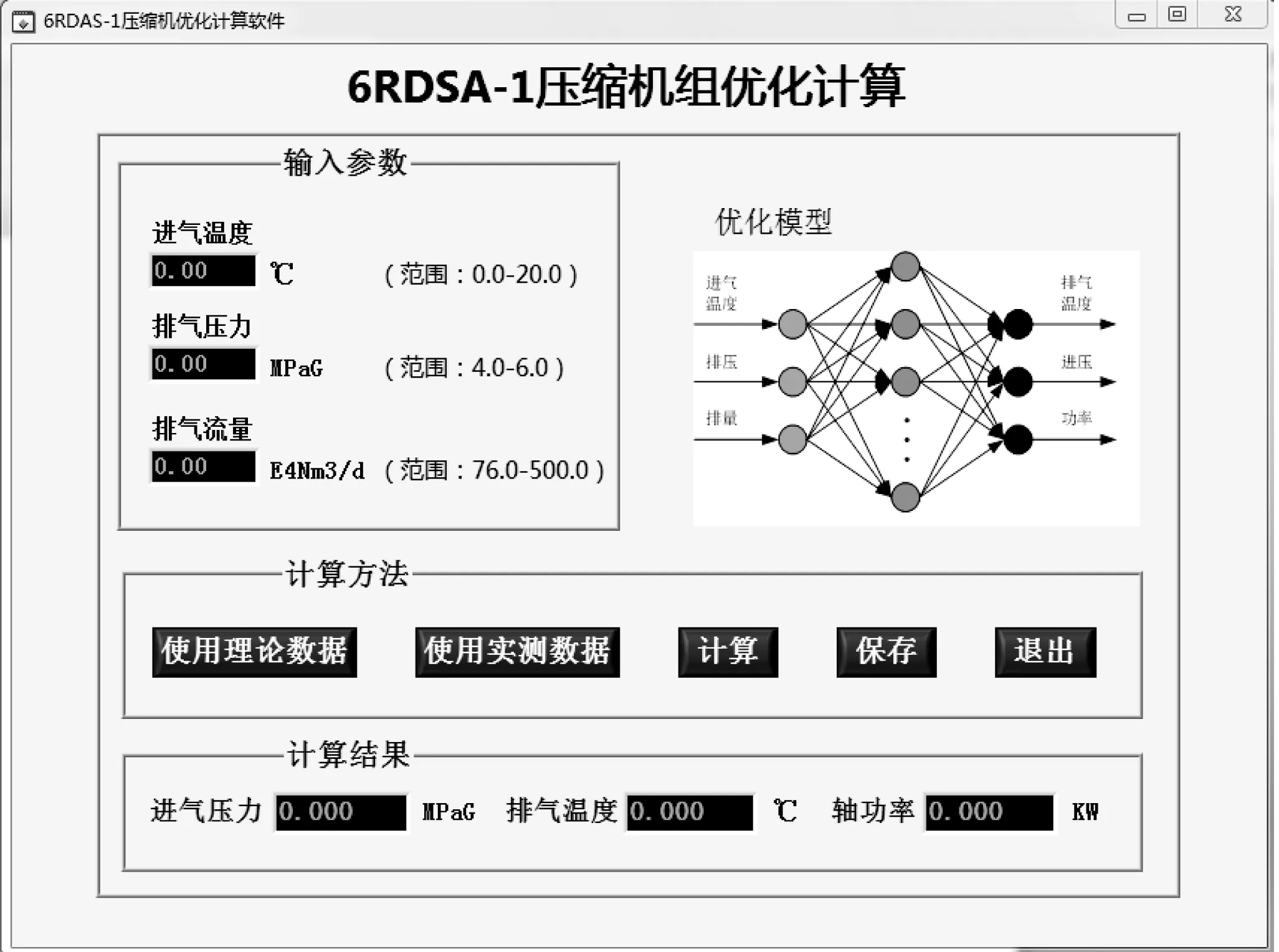
图6 软件输入主界面
图7以使用理论数据进行计算为例,进一步说明该软件的使用及计算过程。在输入参数栏输入相应的进气温度、排气压力和排气流量三个数值,使用数据库中已有理论数据,经过神经网络模型,计算得到进气压力、轴功率和排气温度。现场的工作人员可以根据计算所得进气压力调整压缩机运行工况。根据计算所得轴功率调整压缩机运行组合,制定运行方案,达到压缩机站节能降耗的目的。
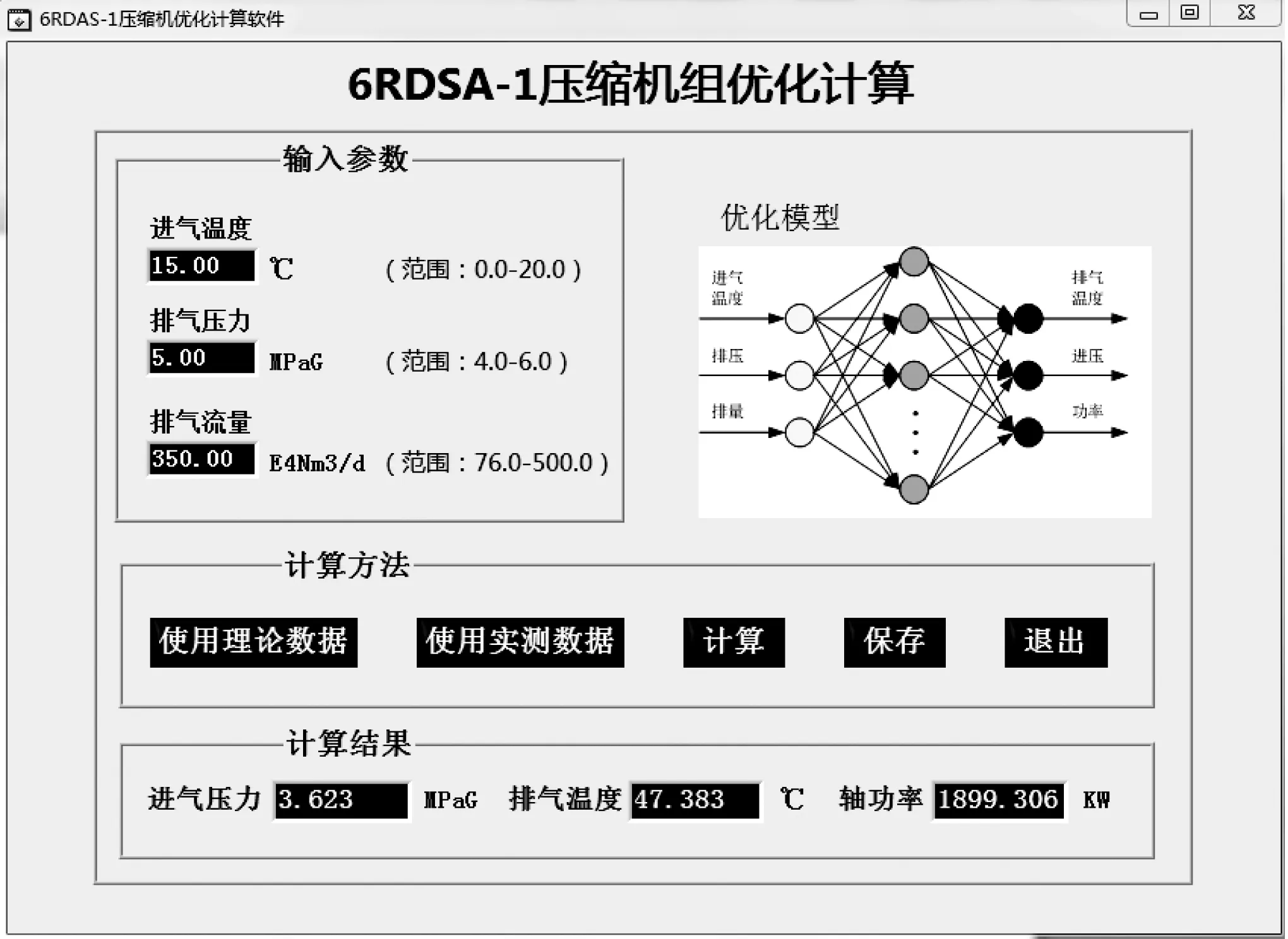
图7 软件计算结果
3.2 压缩机组节能优化软件现场应用
完成压缩机组节能优化软件的开发后,为进一步检验的该软件的可靠性,本文提取了某增压站一个季度内的现场采样数据,采用该软件进行预测,其预测结果与现场实际运行数据的对比如表2、表3所示,相对误差不超过2.75%,满足现场计算要求。

表2 软件预测结果与实际运行结果数据对比

续表2
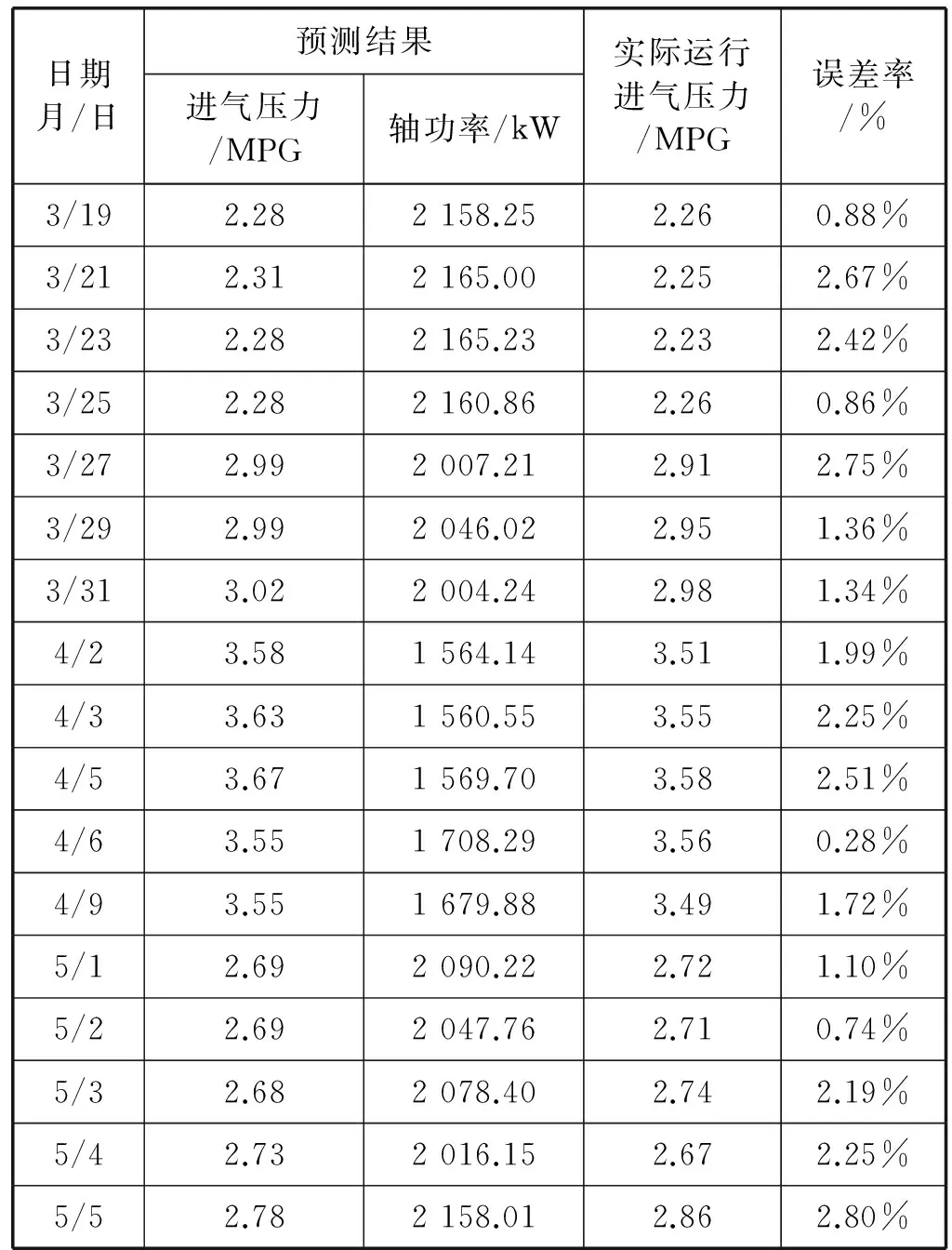
表3 软件预测结果与实际运行结果数据对比

续表3
表4是现场工作人员通过压缩机组节能优化软件预测轴功率,进而制定新的运行方案,对压缩机组投入工作的台数作出及时调整。
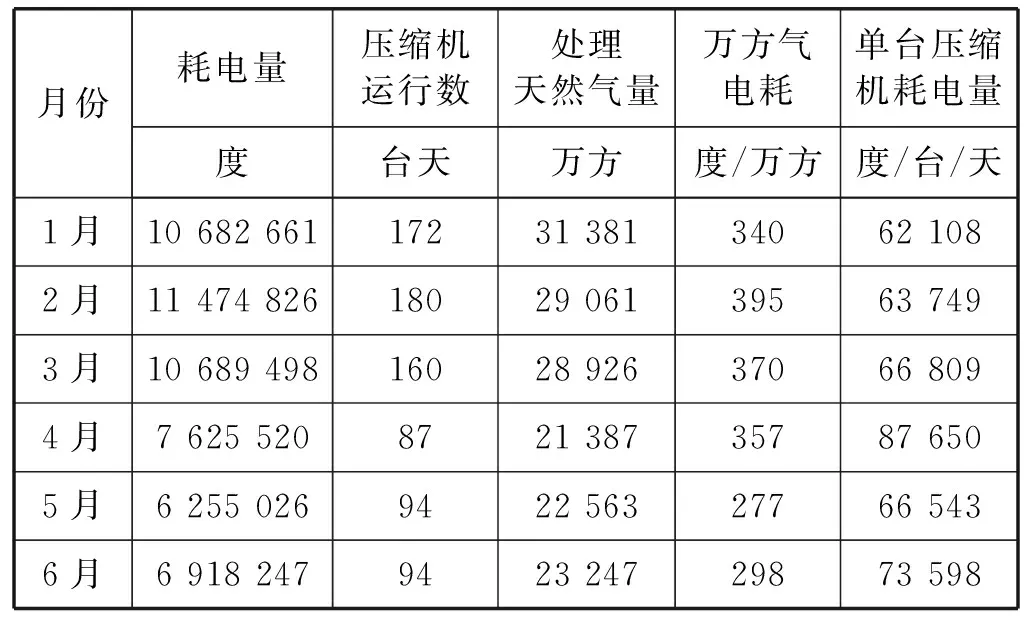
表4 采用软件预测轴功率调整运行台数后的用电量部分数据
该软件经过大量现场实验表明,其对进气压力的预测误差小于2.75%。压缩机组搭配该软件后,通过合理调配压缩机工作台数,节约电量约10%,降低了增压站的运维成本。
4 结 语
(1) 本文所开发的压缩机组节能优化软件,针对输气干线中压缩机的进气压力估算问题,提出了基于BP神经网络的压缩机的进气压力预测方法。该方法在实验室的计算精度不超过1.8%,现场实际运行中的计算精度不超过2.75%,满足现场需求。
(2) 应用本文开发的节能优化软件,以某增压站的6RDSA-1压缩机组为例,建立神经网络模型。通过预测轴功率,提前制定机组运行方案,方便现场调度,在调整运行组合后,节约电能约10%。
(3) 本文所开发的压缩机组节能优化软件是以增压站的6RDSA-1压缩机组为例,但该软件不受压缩机具体型号的限制,可以在“西气东输”输气干线中推广应用。
[1] Mino J. Natural Gas Reciprocating Compressor Optimization[C]//SPE Production and Operations Symposium,Oklahoma City,Oklahoma,USA,23-26 March 2013.
[2] Elshiekh T M. Optimization of Fuel Consumption in Compressor Stations[J]. Oil and Gas Facilities,2014,2(4):59-65.
[3] Garcia-Hernandez A,Alvarado A,Ridens B. Impact of Gas Composition on Pipeline and Compressor Operating Conditions[C]//PSIG Annual Meeting,New Orleans,Louisiana,USA,12-15 May 2015.
[4] 李颖.往复式压缩机节能优化软件开发及典型零部件有限元分析研究[D].浙江:浙江工业大学,2008.
[5] Sun C K, Uraikul V, Chan C W, et al. An integrated expert system/operations research apporach for the optimization of natural gas pipeline operations[J]. Engineering Applications of Artificial Intelligence,2000,13(4):465-475.
[6] Wu S, Rios-Mercado R Z, Boyd E A, et al. Model relaxations for the fuel cost minimization of steady-state gas pipeline networks[J]. Mathematical and Computer Modelling,2000,31(2):197-220.
[7] Chebouba A, Yalaoui F, Smati A, et al. Optimization of natural gas pipeline transportation using ant colony optimization[J]. Computers&Operations Research,2009,36(6):1916-1923.
[8] Mohamadi-Baghmolaei M, Mahmoudy M, Jafari D, et al. Assessing and optimization of pipeline system performance using intelligent systems[J]. Journal of Natural Gas Science and Engineering, 2014, 18(5):64-76.
[9] Rachford H H, Carter R G. Optimizing Pipeline Control in Transient Gas Flow[C]//PSIG Annual Meeting, 28-30 October,Savannah, Georgia. Pipeline Simulation Interest Group, 2000.
[10] Kelling C, Reith K, Sekirnjak E. A Pratical Approach to Transient Optimization for Gas Network[C]//PSIG Annual Meeting, 28-30 October, Savannah, Georgia. Pipeline Simulation Interest Group, 2000.
[11] 汪镭,周兴国,吴启迪.人工神经网络理论在控制领域中的应用综述[J].同济大学学报,2001,29(3):357-361.
[12] 孟召平,田永东,雷旸.煤层气含量预测的BP神经网络模型与应用[J].中国矿业大学学报,2008,37(4):456-461.
[13] KobrunoV A,Priezzhev I. Stable Nonlinear Predictive Operator Based on Neural Network,Genetic Algorithm and Controlled Gradient Method[C]//SEG Technical Program Expanded Abstracts 2015. Society of Exploration Geophysicists, 2015:2941-2946.
[14] 沈花玉,王兆霞,高成耀,等. BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008,24(5):13-15.

