基于混沌系统与改进Zig-Zag变换的图像加密方案

安守楠，吕　翔

(1.中北大学软件学院，山西 太原 030051；2.山西中医药大学)

0　引言

为了保证数字图像在传输中的安全性，对图像加密十分重要。最常用的加密都是采用置乱-扩散的方法。数字置乱是通过特定的技术打乱原图中的像素位置，使其在视觉上变得杂乱无章可循，而扩散则是不改变像素的位置，对像素值进行改变，达到加密的目的。常见的置乱方法有Arnold变换[1]、幻方变换[8]、仿射变换等，但是其实现都较为复杂，安全性较低。

本文采用Zig-Zag变换[15]图像加密方案，有实现简单，复杂度低，密钥周期大的特点，Zig-Zag变换广泛运用于图像加密方案中。

混沌系统的初值与参数极端敏感性、非周期性和长期演化轨道不可预测性等特性与图像加密系统的密钥敏感性、密文呈噪声特性和明文敏感性相对应。文献[3]对Logistic混沌加密系统进行改进，引进两个与明文相关的密钥，提高了安全性。文献[4]对图像从里到外不同范围的各层进行Arnold变换，使得层与层之间的置乱相互干扰，达到打乱Arnold周期性的目的，然后采用斜帐篷映射，对像素值进行扩散。文献[15]利用Zig-Zag变换对彩色图像进行预处理，增强加密效果；在此基础上，利用Zig-Zag变换对预处理后的3个通道进行像素位置的置乱；对三维Logistic混沌序列进行多次处理，实现多次扩散，提高了加密效率和安全性。

基于以上的分析，在对标准Zig-Zag变换改进的基础上，提出Logistic混沌与改进Zig-Zag变换的图像加密方案。首先将标准Zig-Zag进行改进，利用改进后的Zig-Zag[10]变换对图像进行置乱，然后采用Logistic混沌系统[3]产生混沌序列，转化为混沌矩阵，为了达到更好的效果，最后将置乱矩阵与混沌矩阵进行像素值融合，最终得到加密图像。

1　相关知识介绍

1.1　Zig-Zag变换

Zig-Zag[15]是一种扫描置乱的方法。标准的Zig-Zag变换是从图像的左上角元素开始扫描，使其按照“Z”字形向下扫描，获得一维序列，并按照一定方式转换成二维矩阵。但标准Zig-Zag变换仅限于方阵中，而且有些元素位置始终不变，适用性不强，所以对其进行改进。如图1所示。从图1可以看出，1,2,15,16的位置没有发生改变，为了达到更好的置乱效果，对其进行改进，改进后的Zig-Zag变换从右下角开始扫描，按照“Z”字形向上扫描，可以使每个元素的位置发生改变，不仅适合于方阵，还适合于矩阵。如图2所示。从图2可以看出，所有元素的位置都发生了改变。

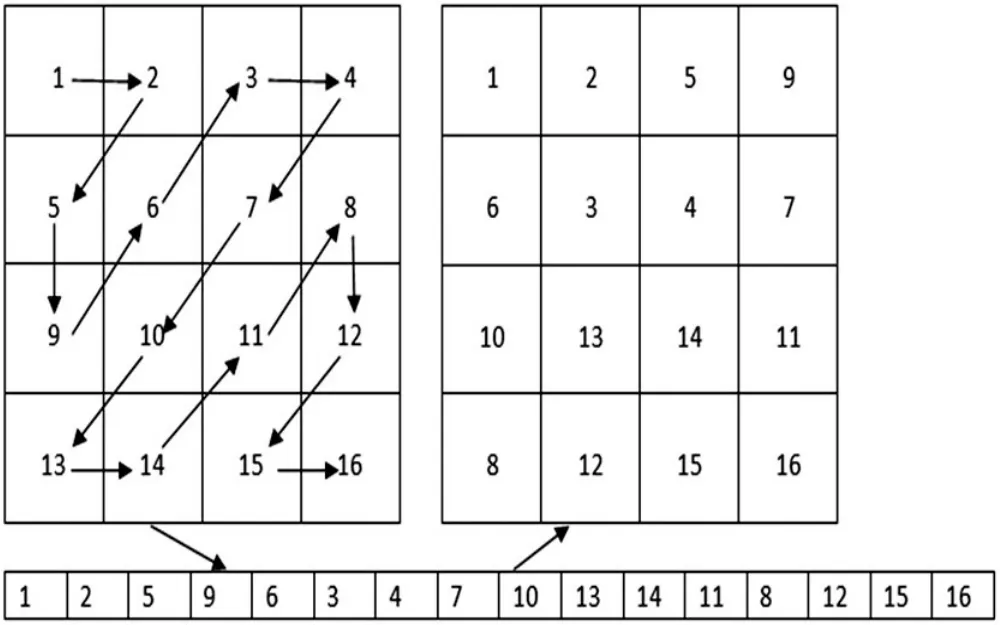
图1　标准Zig-Zag

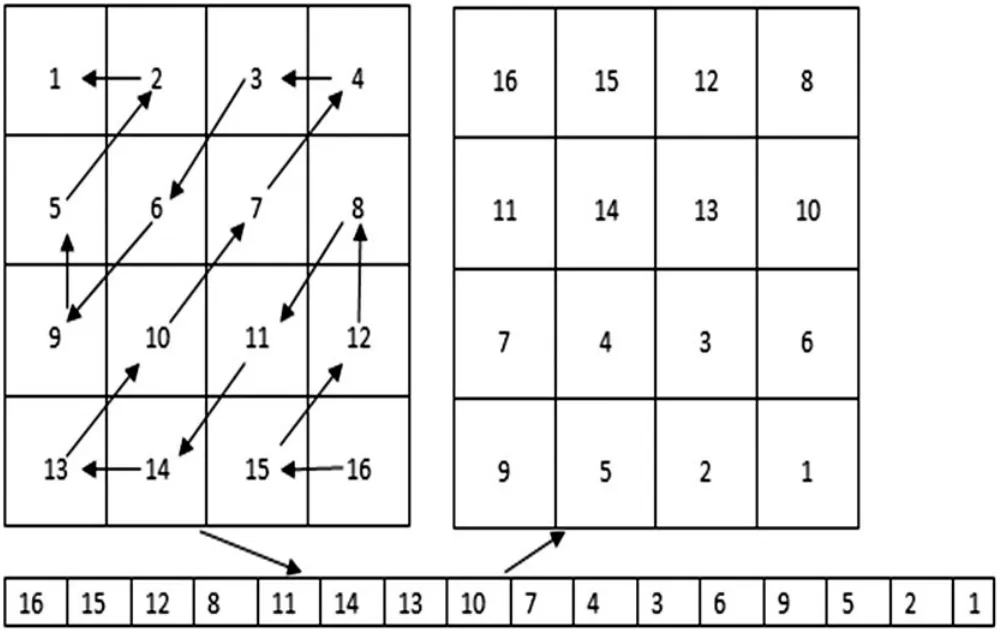
图2　改进后的Zig-Zag

在ZigZag变换过程中，由于矩阵中元素个数有限确定，所以经过有限次Zig-Zag变换后一定可以回到原始状态，即Zig-Zag变换具有周期性。不同维数方阵的Zig-Zag如表1所示，由表 1中可见，Zig-Zag变换拥有更大的密钥周期。

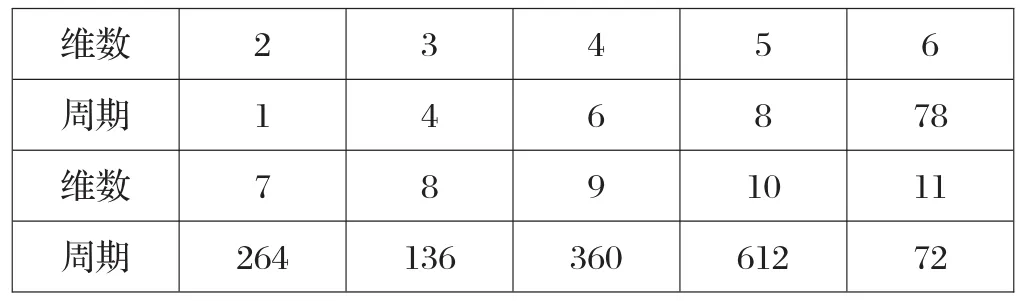
表1　不同维数矩阵Zig-Zag变换周期

1.2　Logistic混沌系统

一维Logistic[16]是目前研究最为广泛的一种混沌映射，其表达式如式⑴所示：

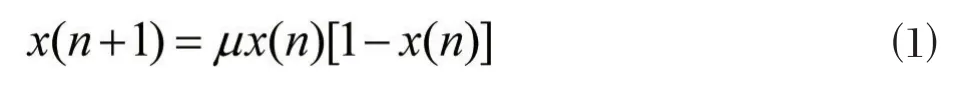
式中x(0)∈(0,1)为初始值，μ∈(3.5699,4]时，系统处于混沌状态。

2　算法描述

2.1　图像加密

设原始图像I的大小为M*N，G(x,y)表示图像I在点(x，y)处的像素灰度值，G'(x,y)表示为加密后的图像在点(x，y)处的像素灰度值。

步骤1将原始图像I进行Zig-Zag变换，次数为p，得到一维序列L，将其按照行优先的顺序转换成二维矩阵A，A的大小为M*N；

步骤2计算图像的像素值总和sum，进行式⑵的处理，给定参数μ，将x(0)和u作为Logistic混沌系统的初始值，迭代式⑴产生混沌序列长度为M*N的混沌序列c(i)，迭代次数为q，对混沌序列中的每个元素进行式⑶的处理，使序列内的每个元素都取值于0-255之间。得到序列c'(i)。

步骤3将序列c'(i)按照行优先的顺序转换成二维矩阵N，矩阵N的大小为M*N。

步骤4将二维矩阵A和二维矩阵N对应位置按照式⑷进行像素值的融合运算，得到加密矩阵I'，即为加密图像。

加密过程如图3所示：

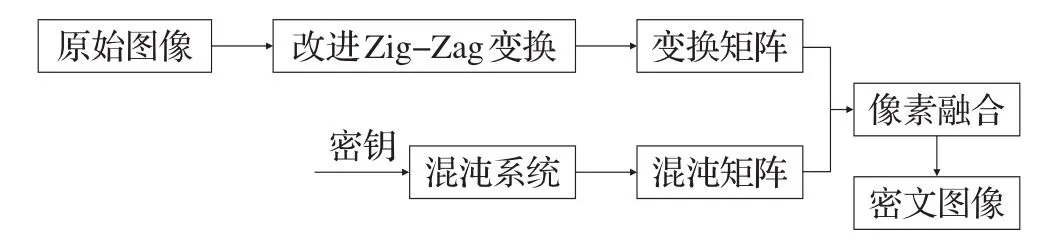
图3　加密过程

2.2　图像解密

图像解密即为加密的逆过程，过程如图4所示。

图4　解密过程

解密过程首先根据密钥x(0),μ将式⑴迭代q次，产生混沌序列，对混沌序列进行式⑵⑶的处理得到混沌矩阵，将密文矩阵与混沌矩阵进行像素值的融合，得到变换绝阵，对变换矩阵进行p次的Zig-Zag反变换，得到原始图像。

3　实验结果与性能分析

本文选取了大量的大小为256*256的灰度图像进行测试，这里给出经典图像lena的加密结果作为代表，本次实验环境是Inter(R)Core(TM)i3CPU,内存为2GB,64位windows7操作系统的PC机，MATLAB2014a，取u=3.7,p=2,q=500，x(0)由计算所得,图5(a)表示原始图像，图5(b)表示加密图像。

图5　实验结果

3.1　密钥空间

具备足够大的密钥空间是一个机密系统加密性能强大的必备条件，本文的密钥有sun,μ,p,q，计算精度按10-15计算，则密钥空间 k=1015*4=1060≈2180，能够有效抵抗穷举攻击。

3.2　密文统计特性

3.2.1　图像直方图

密文特性通常通过直方图表示出来，图像直方图越均匀，表示密文统计特性越好，加密效果越好，实验结果如图6所示。图6(a)表示原始图像直方图，图6(b)表示加密图像直方图。

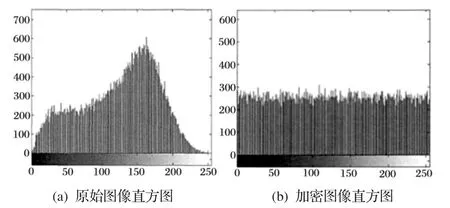
图6

3.2.2　相关性分析

明文图像由于其画面连贯性强，相邻像素的像素值一般比较接近或者相同，存在很强的相关性。攻击者将此作为一个重要的突破口，所以加密后的图像相关性越低说明加密效果越好。本文随机选取明文图像和密文图像相邻的2000对像素灰度值进行比较，计算公式如⑸所示，其中x,y表示相邻像素的灰度值，Rxy为相邻两个像素相关系数。其相关系数表述如表⑵所示。

由公式⑸可以得出表⑵中的数据，说明加密能够破坏其相关性。

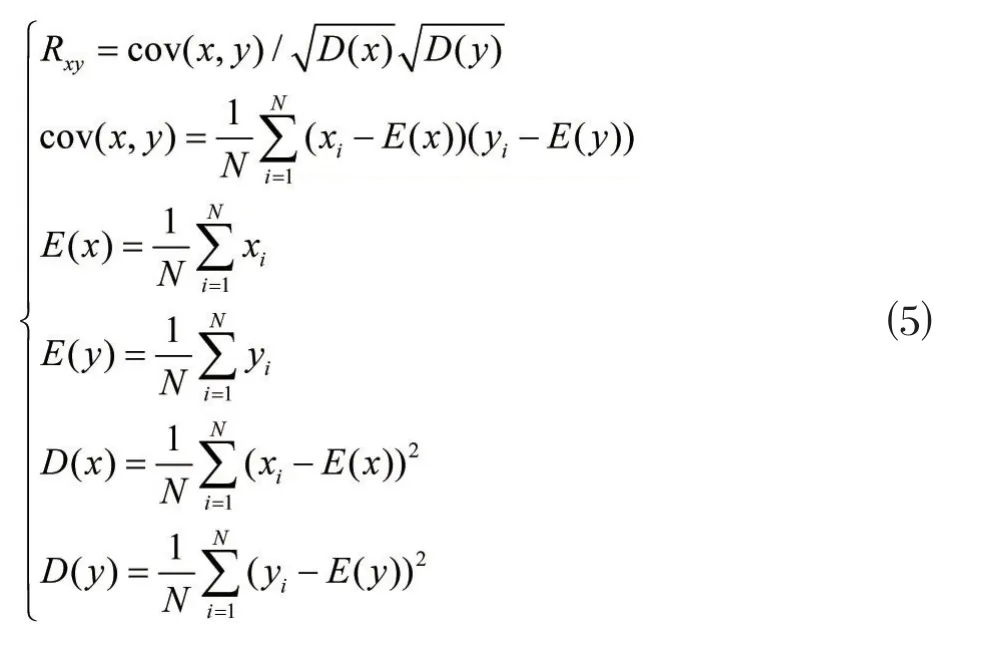
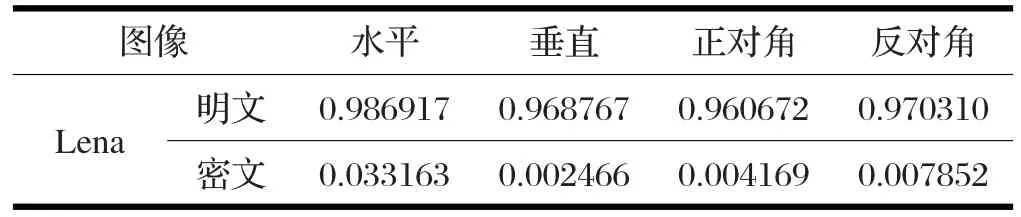
表2　相关系数

3.3　信息熵分析

信息熵反映了图像信息的不确定性，一般认为，信息熵越大，不确定性越大（信息量越大），可视信息越少。信息熵的计算公式如下所示：

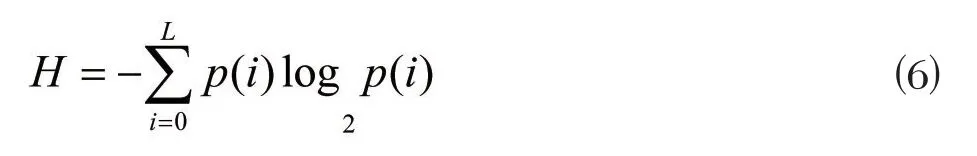
这里，L为图像的灰度等级数，p(i)表示灰度值i出现的概率。对于L=256的灰度值图像，信息熵的理论值为8。通过计算得到本文加密图像的信息熵值为7.999383，接近于理论值（即8），而明文图像的信息熵与理论值有明显差别。

4　结束语

本文在对已有的标准Zig-Zag变换的基础上，对其进行改进，提出了基于混沌序列与改进Zig-Zag变换的图像加密算法，算法基于置乱-扩散的思想，首先将标准Zig-Zag进行改进，利用改进后的Zig-Zag变换对图像进行置乱，然后采用Logistic混沌系统产生混沌序列，转化为混沌矩阵，为了达到更好的效果，最后将置乱矩阵与混沌矩阵进行像素值融合，得到加密图像，实验证明效果良好。

参考文献(References):

[1]李春虎,罗光春,李春豹.基于斜帐篷混沌映射和Arnold变换的图像加密方案[J].计算机应用研究,2018.11:1-2

[2]汤任君,段竞哲,邓洪敏.Logistic混沌序列和DES算法的图像加密方法[J].计算机应用,2017.37(S1):89-92

[3]廖雪峰.基于Logistic混沌系统的图像加密算法分析与改进[J].软件导刊,2017.16(5):39-41

[4]谢国波,苏本卉.基于Arnold分层循环变换的数字图像加密算法[J].计算机工程与设计,2017.38(5):1200-1204

[5]刘会.改进Arnold变换的量子图像加密系统[D].华中师范大学硕士学位论文,2017.

[6]兀旦晖,郑恩让.基于混沌Logistic和Arnold二次加密的图像水印算法研究[J].计算机测量与控制,2017.25(4):193-196

[7]朱淑芹,李俊青.一种混沌图像加密算法的选择明文攻击和改进[J].计算机工程与应用,2017.53(24):113-121

[8]叶满珠,廖世芳,王新芳.基于幻方变换的图像置乱新算法[J].自动化与仪器仪表,2016.2:216-218

[9]朱宁.Arnold加密算法改进[D].山东大学硕士学位论文,2012.

[10]杨玉琴,蒋天发,刘艮.基于扩展Zig-zag变换的数字图像置乱方法[J].信息网络安全,2011.11:57-58,67

[11]何冰.基于仿射变换的图像置乱改进新算法[J].计算机与数字工程,2011.39(3):121-124

[12]郑文斌.基于Zig-Zag扫描的空域图像置乱新算法[J].计算机工程与科学,2009.31(7):50-52

[13]冀汶莉,张敏瑞,靳玉萍,黄兴.基于Zigzag变换的数字图像置乱算法的研究[J].计算机应用与软件,2009.26(3):71-73,87

[14]胡春杰,陈晓,陈霞.基于改进广义Arnold映射的多混沌图像加密算法[J].包装工程,2017.38(3):144

[15]李玉珍,金鑫,赵耿,李晓东,田玉露,王子亦.基于Zigzag变换与混沌的彩色图像加密方案[J].计算机工程与设计,2016.37(8):2002-2006

[16]张永红,张博.基于Logistic混沌系统的图像加密算法研究[J].计算机应用研究,2015.32(6):1770-1773