北斗卫星导航模拟器卫星钟差参数生成方法研究

杨晓昆，李锦清，徐沛虎，胡强

（中国航天科工信息技术研究院，北京 100070）

0 概述

北斗卫星导航系统简称北斗系统，其空间星座由5颗地球静止轨道（GEO）卫星、27颗中圆地球轨道（MEO）卫星和3颗倾斜地球同步轨道（IGSO）卫星组成[1]。北斗导航信号模拟器根据设计的BD-2卫星位置、接收机位置及空间环境影响等仿真计算导航接收机接收到的导航信号观测数据（包括载波相位、伪距和导航电文），采用模拟的方法生成导航接收机接收到的导航信号；并且能够显示系统运行时的BD-2卫星和导航站的位置、接收机载体的运行轨迹和各种参数。其中一项关键的参数就是卫星钟差参数。

卫星钟差采用二阶多项式表示：

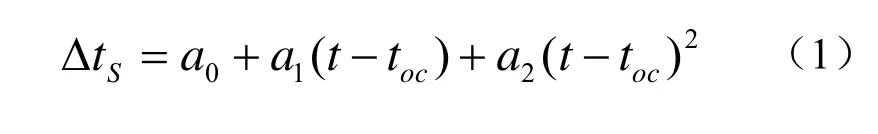
a0：星钟偏差，相对于系统时间的偏差；

a1：钟速，相对于实际频率的偏差系数；

a2：半加速（频率漂移的一半）。

卫星钟一般为铷钟或铯钟，铷钟和铯钟的性能不尽相同。

钟差参数a0、a1、a2的获取可以分为两种方式：

（1）钟差参数法

钟差参数可以由用户通过界面设定，并可保存在文件中；也可从文件中读取。

（2）拟合参数法

从文件中读取钟差值，通过拟合计算得到钟差参数[2]。拟合方法采用最小二乘法。国际GNSS服务（International GNSS Service, IGS)于1994年进入完全运行状态后开始提供 GPS精密星历[3]。目前IGS网站上能下载各个GPS分析中心提供的精密卫星钟差文件[4]。IGS及数据分析中心提供15分钟和5分钟间隔的精密卫星星历[5]。有关北斗钟差数据可以从IGS网站上得到。文件日期为2016年2月21日的 The Extended Standard Product 3 Orbit Format（SP3-d）文件包含了关于北斗卫星数据的说明。

1 最小二乘法拟合和楚列斯基方法矩阵求解

拟合计算的目的是估计在已知公式中的未知参数。一般情况给出函数及其在N个不同点的测量值要确定未知参数与各对应量之差的平方和最小。

对于不依赖于参数ak的给定函数kα,k=1,2,...n,有

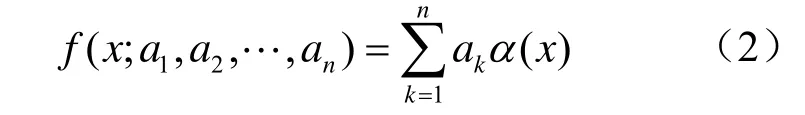
于是要求解的方程是线性误差方程[6]：

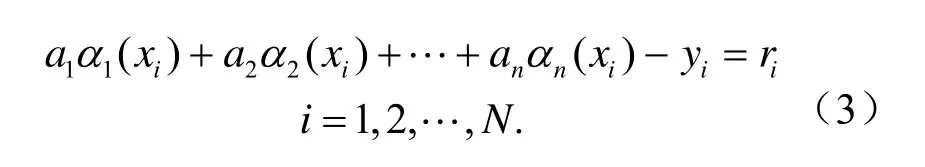
则误差平方和为[6]：

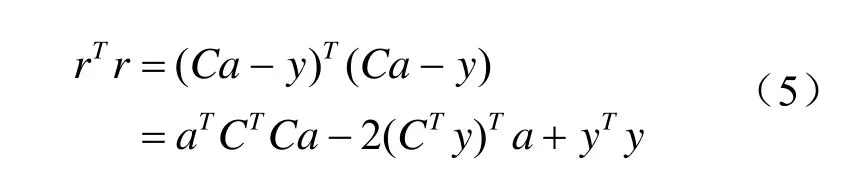
解这个方程组，本研究采用楚列斯基分解法，但需要证明矩阵A是对称正定矩阵，从可以判断为对称阵，其正定性证明如下：

Z是非零向量。

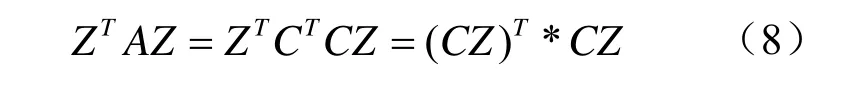
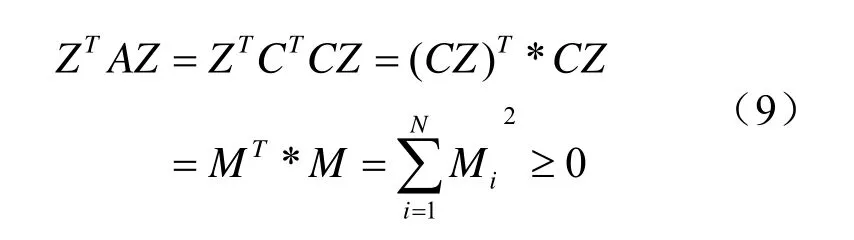
因此A为半正定矩阵。只要找出任一个Mi不等于0，则A为正定阵。

由于：

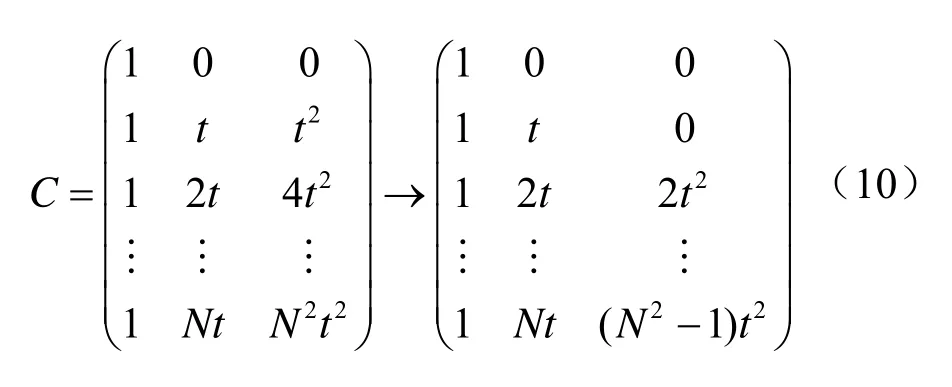
式（10）中最后一个矩阵由第 3列减去第二列乘t得到，t不等于0，因此矩阵C的3列向量线性无关，表示为是非零向量，因此如果M=0则矩阵C的3个列向量线性相关，与矩阵C的3列向量线性无关矛盾，因此Mi中一定有一个数不为0，则A为正定阵。

为求解对称正定的非齐次线性方程组Ax-d=0，利用系数矩阵A的性质可以给出有效的算法，即楚列斯基分解：

其中B是对角元素为正的正则下三角矩阵。根据矩阵方程

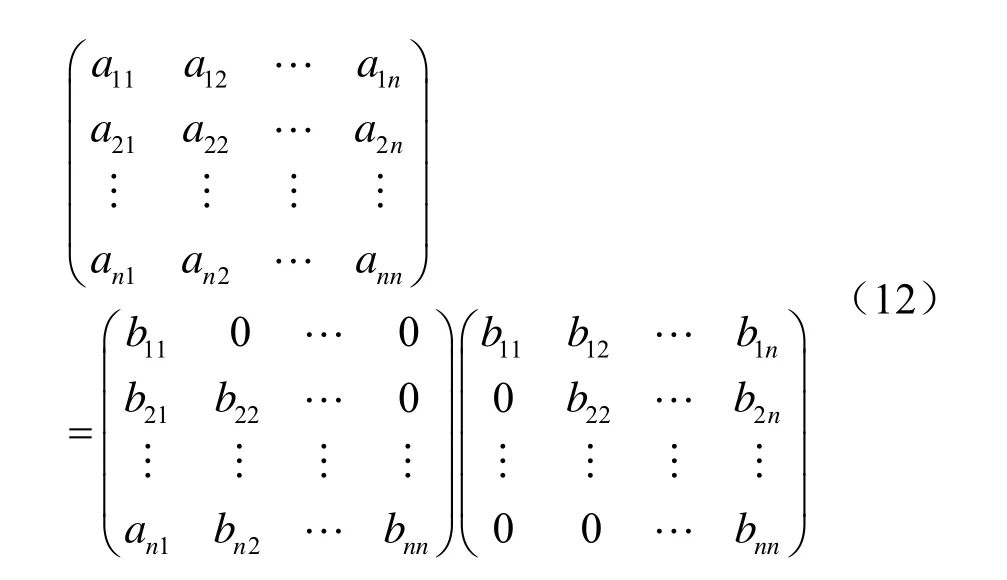
则有下列关系式[6]：

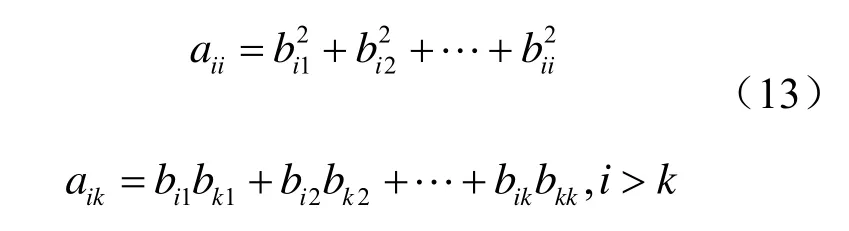
从式（13）中可以得出[6]：

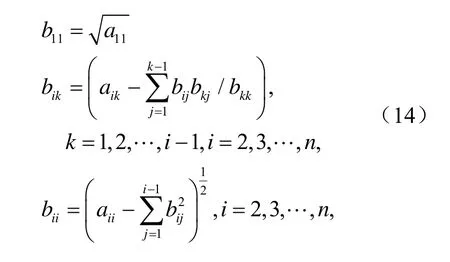
为完成对称正定矩阵A的楚列斯基分解，只需依次计算下三角矩阵B的元素并存入矩阵A的存储区。这不仅可以有效利用存储空间，而且减少计算量。

根据A的楚列斯基分解，求解线性方程组Ax-d=0的推导过程如下：

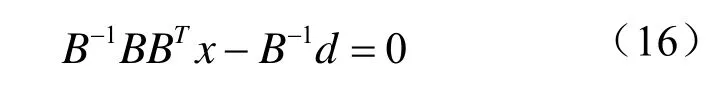
得到：

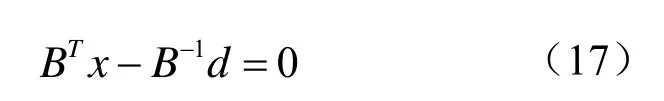
由此得到：

因此楚列斯基方法步骤为：

（1）A=BBT（楚列斯基分解），

（2）BC-d= 0（向前代换，求C），

（3）BT x-C= 0（逆代换，求x）。

表1 仿真得到的卫星钟差参数表

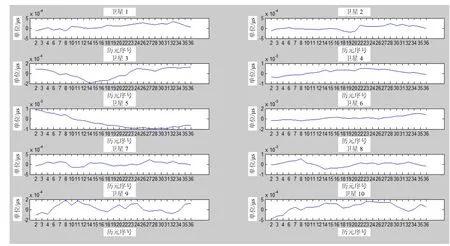
图1 钟差误差图

2 仿真结果分析

以IGS 2016年10月14日1点50分0秒的1到10号星数据为例，每隔20分钟取一组值，构建矩阵，经楚列斯基分解法解算后得到一组参数值，如表1所示。以此参数计算每隔5分钟的钟差，去掉拟合参数用到的钟差，与SP3文件中给出的钟差做对比，误差图如图1所示，从图中可以看出，时刻1,5,9,13,17,21,25,29,33被去掉，时刻间的时间差为5分钟。仿真误差最大的为6号星，最大误差为1.02ns，因此1到10号星的仿真误差在1.1ns以内，满足模拟器使用需求。

3 结论

北斗卫星导航模拟器卫星钟差参数生成方法主要有两种，在已知参数的情况下可以直接赋值使用，在未知参数情况下可以利用最小二乘法拟合方法求解卫星钟差参数。本文给出了北斗导航卫星的钟差参数拟合算法，给出了关键部分证明过程，并用实际计算实例验证了计算方法的合理性。

参考文献：

[1]中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件(公开服务信号 B1I（1.0版）[Z].2012.

[2]杨俊 等著. 卫星导航信号模拟源理论与技术[M]. 北京：国防工业出版社, 2015.

[3]陶庭叶, 高飞, 李晓莉.一种高精度 GPS卫星钟差预报方法[J]. 中国空间科学技术, 2013.

[4]曹凤志, 方书山. 精密卫星钟差内插的埃尔米特方法[J].GNSS World of China, 2011.

[5]王波, 张书毕, 益斌, 卞和方. 精密 GPS卫星钟差两种插值方法的比较[J]. 全球定位系统, 2007.

[6]埃伯哈德·蔡德勒等编. 文林等译. 数学指南-实用数学手册[M]. 北京: 科学出版社, 2012.

[7]王能超 编著. 数值分析简明教程[M]. 武汉: 华中科技大学出版社, 2012.