航天发射场液体推进剂的泄漏扩散模型研究*

柳宁远，崔村燕，辛腾达，栾　骁

(1. 航天工程大学 研究生管理大队，北京 101416；2. 航天工程大学 航天装备系，北京 101416；3. 中国人民解放军63618部队，新疆 库尔勒 841001 )

0　引言

随着航天事业的发展，发射任务密集，发射场安全问题显得尤为重要。液体导弹推进剂UDMH毒性较强，一旦发生爆炸或推进剂泄漏事故，有毒推进剂的逸散会对发射塔架周边的人员安全和环境造成巨大危害[1]。因此，有必要对泄漏事故进行快速评估，分析不同泄漏时间有毒推进剂在大气中的扩散范围以及人员危害区域，以便及时采取防护措施，保证人员的安全。

对危害性气体扩散过程的数学模拟以及正确估算各种条件下危害性气体浓度随时空的分布和变化，关键在于扩散模型在各种条件下的应用。国内外关于不同条件下气体扩散模型的应用有比较多的研究，包括高架源气体泄漏，滨海地形大气扩散，城市污染气体扩散，火灾烟雾扩散等[2];关于发射场推进剂泄漏情形下的扩散研究较少，陈新华等提出了爆炸后残余推进剂蒸发形成的毒气在大气中扩散的解析解[3]，但对于扩散模型在该情形下的适用性有待进一步研究。

本文针对扩散模型在航天发射场推进剂气体扩散的适用性进行研究，结合推进剂偏二甲肼在航天发射场蒸发扩散的条件，对扩散模型进行完善并建立数学模型，并通过扩散模型计算结果和对应数值模拟结果及已有实验结果进行对比分析，为航天发射场扩散模型的建立和完善提供参考。扩散模型的建立有利于事故后快速估算有毒推进剂浓度分布，为泄漏事故危害性评估和防护提供依据。

1　扩散模型建立

1.1　理论模型及基本假设

根据梯度输送理论，由湍流运动引起的局部位置质量通量与该位置扩散物质的平均浓度梯度成正比。式(1)为根据梯度输送理论导出的普遍形式湍流扩散方程，说明流体中某物质的散布是由湍流扩散所引起的。x，y，z方向的湍流扩散系数分别为Kx，Ky，Kz，扩散系数为时空的函数，与流场形式有关[4]。

(1)

若将坐标系x轴与风向取一致，z轴垂直向上，假设流场在3个方向的扩散系数为常数(即斐克扩散情形)，则湍流扩散方程可简化为：

(2)

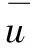
(3)

为简化计算，略去x方向的湍流项。

当x>0时，

(4)

当z→0时，

(5)

求解可得，有风时连续点源浓度分布为：

(6)

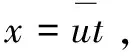
(7)

1.2　扩散模型在发射场推进剂蒸发扩散中的应用

航天发射场附近地势平坦开阔，气象稳定，符合平稳均匀湍流的假设，粒子扩散位移符合正态分布形式，风速一般大于1 m/s，符合上节所述扩散模型和基本假设，但根据实际情况需要进行改进完善。

液体火箭意外发生爆炸时，部分推进剂在高温下蒸发成高温气体迅速扩散，部分液体推进剂散布在周边缓慢蒸发。计算模型只适用于缓慢蒸发的推进剂，高温气体随冲击波迅速扩散至远处，相对影响较小，在计算中不予以考虑。

1.2.1残留推进剂泄漏源强

残留推进剂散布在不规则区域，面积为Aw，对于面源的源强计算，可通过污染区面积和污染区推进剂蒸发速率来估计：

(9)

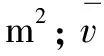
以偏二甲肼(UDMH)为例，偏二甲肼在土壤中的蒸发速率为[5]：

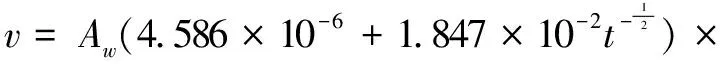
(10)

式中：v为大气环境下土壤中液体蒸发速率，kg/(m2·s)；ps,f为UDMH饱和蒸汽压，Pa；p为发射场当地大气压，Pa；u∞为平均风速，m/s；up为参考风速，计算时取5m/s。

液体推进剂偏二甲肼与四氧化二氮分子量比空气大，且易于反应分解。对于气体和很小的粒子沉降作用可忽略不考虑，但是由于湍流扩散和布朗运动沉积到各种表面，被吸收或者发生其他反应会对其有一定消耗，故为对公式中的泄漏源强度Q进行修正，以考虑空气中污染物质的量的减损[6]。

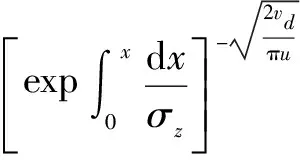
(11)

式中：vd为沉积速度，m/s，取值0.01。

1.2.2地面反射效应

残留推进剂分布在地表，属于地面泄漏源。由于地面的反射造成污染物浓度的上升，为简化计算，假设为全反射的情况，泄漏浓度则是无界条件下的2倍，即：

(12)

1.2.3残留推进剂等效面源扩散

呈面块散布的污染物排放源称为面源，按照点源扩散公式可以沿x，y方向积分得到。

(13)

为了简化模型快速计算，也可以采用虚点源法，将面源化为点源处理。使得由虚点源排放的污染物经过虚拟距离x0后，与面源具有同样的扩散幅。

(14)

常采用经验方法给出初始扩散幅：

(15)

则地面浓度有：

(16)

空间浓度分布：

(17)

1.2.4扩散参数的确定方法

根据湍流统计理论，气体在随机流场中的扩散能力和散布范围由大气扩散参数来体现。对应x，y，z3个方向分别用σx，σy，σz表示，随着下风距离x变化而变化。当风速大于一定值时，x方向的湍流扩散可以忽略不计。所以，在不同的高斯烟羽模式中，确定大气扩散参数的关键在于确定不同条件下不同的扩散参数σy，σz。扩散系数σy，σz的大小与大气湍流结构，离地高度，地面粗糙度，泄漏持续时间，抽样时间间隔，风速，以及离泄漏源的距离等因素有关。根据地面气象观测数据，对大气的扩散能力进行判别，分为A，B，C，D，E，F共6类大气稳定度扩散级别。每个扩散参数对应每1类大气稳定度有1条扩散曲线，表示扩散参数随下风距离x的变化。根据曲线就可以确定某区域确定稳定度下下风距离x的大气扩散参数的值。

1)确定大气稳定度级别

大气稳定度可以分为A，B，C，D，E，F 6类，按照从不稳定到稳定依次分级，如表1～2所示。这里采用的是D.B. Turner所提出的用太阳高度角来定量判定日照强度的方法[7]。

表1　由太阳高度角确定日照强度与等级

表2　Turner的稳定度分级方法

Turner的分级方法定量相对比较确切，只要有地面风速，云量和云高的观测数据，就可以确定稳定度级别，是实际应用中更为普遍使用的方法。

2)根据大气稳定度级别选择扩散参数曲线

按照相应的大气稳定度级别确定扩散参数曲线，大气扩散参数曲线可以有多种表达方式。比如，参数表达式，观测点数据，曲线表示等，可以根据不同需要按照下风向距离x确定扩散参数确定具体位置的大气扩散参数的值[7]，如表3所示。

表3　不同大气稳定度下扩散参数关于下风向距离x的表达式

2　数值模拟

结合航天发射场的气体泄漏的实际情况，通过理论分析得到的气体计算方程，其准确性需要试验数据的验证。目前，比较可行的试验方法有数值模拟方法和实测试验方法，数值模拟计算全面精确，便于分析，但为简化条件和实际情形有一定差异；实测试验结果相对有说服力，但存在测量误差和偶然误差。综合考虑，拟采用对比分析的方法弥补各自局限性。

2.1　数值模拟

对地面源泄漏过程进行数值模拟，假设泄漏源为连续泄漏源，泄漏源等效面积为1 m2，位于计算域下风向10 m处地面。计算区域高度在100 m以下，不考虑大气的分层现象，假设初始条件计算区域空气均匀分布，计算域的几何模型如图1所示。

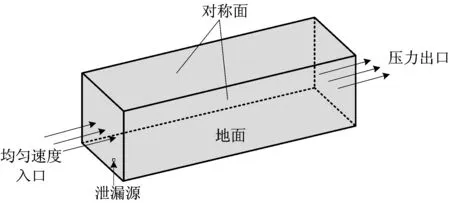
图1　几何模型示意Fig.1　Geometric model

偏二甲肼蒸发速率主要受到蒸发面积、风速、温度和湿度等因素的影响，且满足如下计算公式：

(18)

式中：Aw为大气环境下土壤中液体蒸发面积，m2；ps,f为UDMH饱和蒸汽压，Pa，取20 kPa；p为发射场当地大气压，Pa；u∞为平均风速，m/s；up为参考风速，计算时取5 m/s。假设计算区域风向不变，风速为3 m/s，压强为89 200 Pa，空气湿度20%，温度30 ℃。则蒸发速率为：

(19)

将蒸发速率作为液池表面的速度边界条件代入数值计算，模拟地面残留推进剂蒸发的扩散。

在数值计算中主要采用有限元方法，描述偏二甲肼在开放空间内泄漏扩散过程的基本控制方程主要有气体状态方程、流体连续性方程，质量方程、动量方程、能量方程和组分输运方程。

经数值模拟计算所得的地面偏二甲肼浓度分布如图2～3所示。从图中可以定性分析得到：扩散浓度呈对称分布，说明扩散作用垂直于下风向的方向上大小相同。

图2　600s地面偏二甲肼体积浓度分布Fig.2　600s UDMH volume fraction on the ground

图3　垂直下风向截面偏二甲肼体积浓度分布Fig.3　UDMH volume fraction of vertical downward direction

图4　下风向不同距离地面体积浓度分布Fig.4　Volume fraction curve of different downwind distance on the ground

如图2～3所示，扩散的偏二甲肼气体主要分布在下风向，下风向分布范围远大于其他方向，说明平流输送对扩散的作用远大于湍流扩散的作用。

取下风向10，30，50，90 m处，地面偏二甲肼浓度绘制曲线，如图4所示。浓度分布符合正态分布，与计算公式及统计规律相吻合。

2.2　实验结果对比验证

2.2.1实验条件

推进剂扩散实验危险性较大，成本较高[11]，故采用已有实验数据进行相关比较与验证。陈新华等针对液体火箭推进剂爆炸毒气逸散做过大量的实验研究[8]，以其中相关实验结果与数值模拟及计算公式结果进行对比。

实验模拟推进剂爆炸后毒气扩散过程，大气中毒气浓度分布情况，爆炸后计算地面残留推进剂量，并对地面残留推进剂蒸发扩散的浓度分布进行检测分析。大气中浓度采样是利用电动吸气式大气采样器进行，9个采样点分布在下风向不同距离，有毒气体通过吸气管进入吸收液，事后对吸收液进行检测分析。

实验的主要环境条件[9]为：气压89 200 Pa，温度29℃，风速1～3 m/s，空气湿度19%，大气稳定度D类。环境条件与数值模拟的假设条件基本一致，可以认为是相同条件下的蒸发扩散过程。

2.2.2采样点数据比较

采样点位置的数值模拟结果和扩散模型计算结果如表4所示。

表4　实验测量值、数值模拟值和扩散模型值

图5　采样点位置实验值Q1、数值模拟值Q2和扩散模型计算值Q3比较Fig.5　Comparison between test measurements,numerical simulations and diffusion model values

比较数值模拟值与扩散模型计算值，扩散模型计算值整体小于数值模拟值，两者相关度较大，同一位置浓度偏差在15%左右，最大不超过20%。由于采样点每3个点在同一下风向距离，图5三点线段图可以看出，同一下风向距离，正对泄漏源的位置浓度最高，两侧浓度呈对称衰减分布。对称衰减分布的特征，与上一节定性分析结论相一致。

比较实验测量值、数值模拟值与扩散模型计算值，实验测量值与数值模拟值和扩散模型计算值相近，且普遍偏大。图5三点线段图中，实验测量值存在个别点(采样点8)有比较大的偏差，质量浓度值比数值模拟及计算值小，但与同一下风向距离的2个点数值相近。

2.2.3原因分析

测量值较大，分析可能有2个原因：爆炸后迅速蒸发的推进剂气体残留导致浓度增加；推进剂爆炸燃烧改变了局部温度，改变了大气的稳定度，也改变了气体扩散能力，使得浓度增加，扩散模型计算中扩散参数应该进行修正。

图5三点线段图中，存在个别点有比较大的偏差，且在同一下风向三点中，峰值减小。分析认为，实际测量过程中风向会有变动，局部气流会影响到气体扩散浓度，而扩散模型计算和数值模拟计算忽略这种情况的理想条件，会导致存在一定的偏差。另外，考虑到测量的方法比较粗糙，也存在偶然误差和测量误差的可能。

总体来看，实验测量值与数值模拟值及计算值的相关度较大，但实验值偏大，存在多种因素影响，在爆炸燃烧后泄漏扩散情形下，应对计算公式进行参数修正使其满足安全和精度要求。

3　结论

1)气体扩散模型与数值模拟及实验结果基本一致，趋势相同，数值整体偏小；说明扩散模型能较好地反映气体扩散的浓度分布，但存在一定偏差。

2)由于推进剂燃烧和氧化反应，扩散区域温度上升，大气稳定度降低，故实际浓度比理论计算值大。

[1]丛继信, 王力, 张光有.液体推进剂职业中毒风险评价及防护对策研究[J].中国安全生产科学技术,2012,8(7):40-45.

CONG Jixin,WANG Li,ZHANG Guangyou.Study on risk assessment and protective solutions for occupationalpoisoning of liquid propellant[J].Journal of Safety Science and Technology,2012,8(7):40-45.

[2]任建国, 鲁顺清. 气体扩散数学模型在安全评价方面的应用[J]. 中国安全科学学报,2006,16(3):12-16.

REN Jianguo, LU Shunqing. Application of gas diffusion mathematical model to safety assessment[J].China safety science journal, 2006,16(3):12-16.

[3]陈新华, 武江涛, 佟连捷，等. 液体火箭爆炸后毒气扩散研究[J]. 推进技术,1999,20(5):6-10.

CHEN Xinhua, WU Jiangtao, TONG Lianjie，et al.Research on Toxic gas diffusion after liquid propellant rocket explosion[J]. Journal of Propulsion Technology, 1999,20(5):6-10.

[4]蒋维楣, 孙鉴泞, 曹文俊，等. 空气污染气象学教程[M]. 北京:气象出版社,2004.

[5]陈新华, 庄逢辰. 液体火箭推进剂在自然环境中蒸发特性[J]. 热科学与技术, 2005,4(4):304-308.

CHEN Xinhua, ZHUANG Fengchen. Analysis of liquid rocket propellant evaporation characteristic in natural environment[J], Journal of Thermal Science and Technology, 2005,4(4):304-308.

[6]M.Adon, C.Galy-Lacaux, C.Delon， et al. Dry deposition of nitrogen compounds (NO2, HNO3, NH3) sulfur dioxide and ozone in west and central African ecosystems using the inferential method[J]. Atmos. Chem. Phys., 2009(13):11351-11374.

[7]D.B.Turner. Workbook of atmospheric dispersion estimates: an introduction to dispersion modeling[M]. NYC:CRC Press, 1994.

[8]SAFITRI, X.Gao, M. S. Mannan. Dispersion modeling approach for quantification of methane emission rates from natural gas fugitive leaks detected by infrared imaging technique[J]. Journal of Loss Prevention in the Process Industries, 2011,24(2):113-120.

[9]陈新华, 向四桂. 航天发射场有毒气体污染范围安全性研究[J]. 指挥技术学院学报,2001,12(3):59-62.

CHEN Xinhua, XIANG Sigui. Study of Safety in pollution Range of poisonous gas to space vehicle launching site[J]. Journal of Institute of Command and Technology, 2001,12(3):59-62.

[10]陈新华.液体火箭推进剂爆炸毒气逸散理论与实验研究[R].北京：装备指挥技术学院,2001.

[11]吴玉剑,潘旭海.障碍物地形条件下重气泄漏扩散实验的CFD模拟验证[J].中国安全生产科学技术,2010,6(3):13-17.

WU Yujian，PAN Xuhai. Simulation and verification of CFD on dispersion of heavy gas leakage in obstacle terrain[J].Journal of Safety Science and Technology,2010,6(3):13-17.